变边界下考虑起始水力坡降的软土固结数值解
2023-01-05姚宝宽冯翠霞李传勋
姚宝宽, 陈 余, 冯翠霞, 李传勋
(1.江苏省地质局 第三地质大队,江苏 镇江 212001; 2.江苏大学 土木工程与力学学院,江苏 镇江 212013; 3.上海申元岩土工程有限公司,上海 200011)
0 引 言
一般求解地基固结问题(如经典Terzaghi固结模型)时,常将天然地基排水边界视作理想化的完全透水或完全不透水边界,但真实的土层边界透水性大多数是介于完全透水与完全不透水之间的。基于以上认识,文献[1]在已有的部分排水边界基础上考虑边界透水性与时间的相关性,提出土层边界透水性能随时间指数变化的变排水边界。相比于完全透水边界、完全不透水边界及部分透水边界,变排水边界更具有普遍适用性,且其可退化为完全透水边界。当边界排水能力强(界面参数大)时,排水边界的超静孔压值可以近似看作0,即当边界相关参数满足一定条件时,变排水边界的固结模型可视为完全透水边界模型。
目前,对于变边界下的土体一维固结理论,已有一些研究成果。文献[2]建立变边界下均质地基单面排水固结模型,并分析变边界下土体固结性状;文献[3]利用ABAQUS有限元对变边界下的成层地基固结进行计算,分析变边界与传统边界间的差异;文献[4]考虑土体的非线性压缩与渗透特性,得到变边界下土体一维非线性固结模型解析解,进一步分析变边界对非线性固结性状的影响;文献[5]给出单级等速加载下,考虑变边界影响的土层一维固结模型解析解;文献[6]考虑土体的流变特性对固结的影响,建立变边界下土体的一维流变模型,并给出其对应的解析解,分析不同因素下固结性状的异同;文献[7]采用分数阶Kelvin模型描述土体的流变特性,建立变边界下饱和黏性土体一维分数阶导数黏弹性固结模型,并给出相应解;文献[8]在城市固废一维降解固结模型中考虑变边界的影响,获得模型解析解,并分析不同边界下城市固废降解固结性状的差别。
上述基于变边界的固结理论分析均认为Darcy定律能有效地描述土中渗流,但室内试验和实测数据均表明软黏土中渗流会出现偏离Darcy定律的现象[9-14]。若低水力坡降下黏性土中的水渗流被完全忽略,则土中水的渗流规律可近似为文献[14]中提出的具有起始水力坡降的渗流模型。黏性土中渗流存在的起始水力坡降势必导致土体固结过程与Darcy定律下有所不同。文献[15]给出了基于起始水力坡降的土体固结差分解和近似解,在此基础上,文献[16-23]分别在考虑起始水力坡降的土体非线性固结、大变形非线性固结、流变固结等方面取得进展,这些研究表明,土中渗流存在的起始水力坡降对土体固结过程影响甚大,其对固结的影响不容忽视。
目前已有的软土固结相关研究成果均认为土层的排水边界为完全排水边界或完全不排水边界,同时考虑随时间变化的变边界和起始水力坡降的固结理论研究报道很少,因此,研究变边界下考虑起始水力坡降的固结问题具有一定的理论和实际意义。本文引入随时间指数变化的变边界及软黏土中存在的起始水力坡降,建立单层均质土体的一维固结模型;利用有限差分方法对该固结模型进行数值求解,分别获得土层超静孔压、土层固结度的数值解;最后,利用数值解深入分析变边界及起始水力坡降对固结性状的影响。
1 边界条件分析及固结模型建立
1.1 控制方程
软土地基一维固结模型如图1所示。
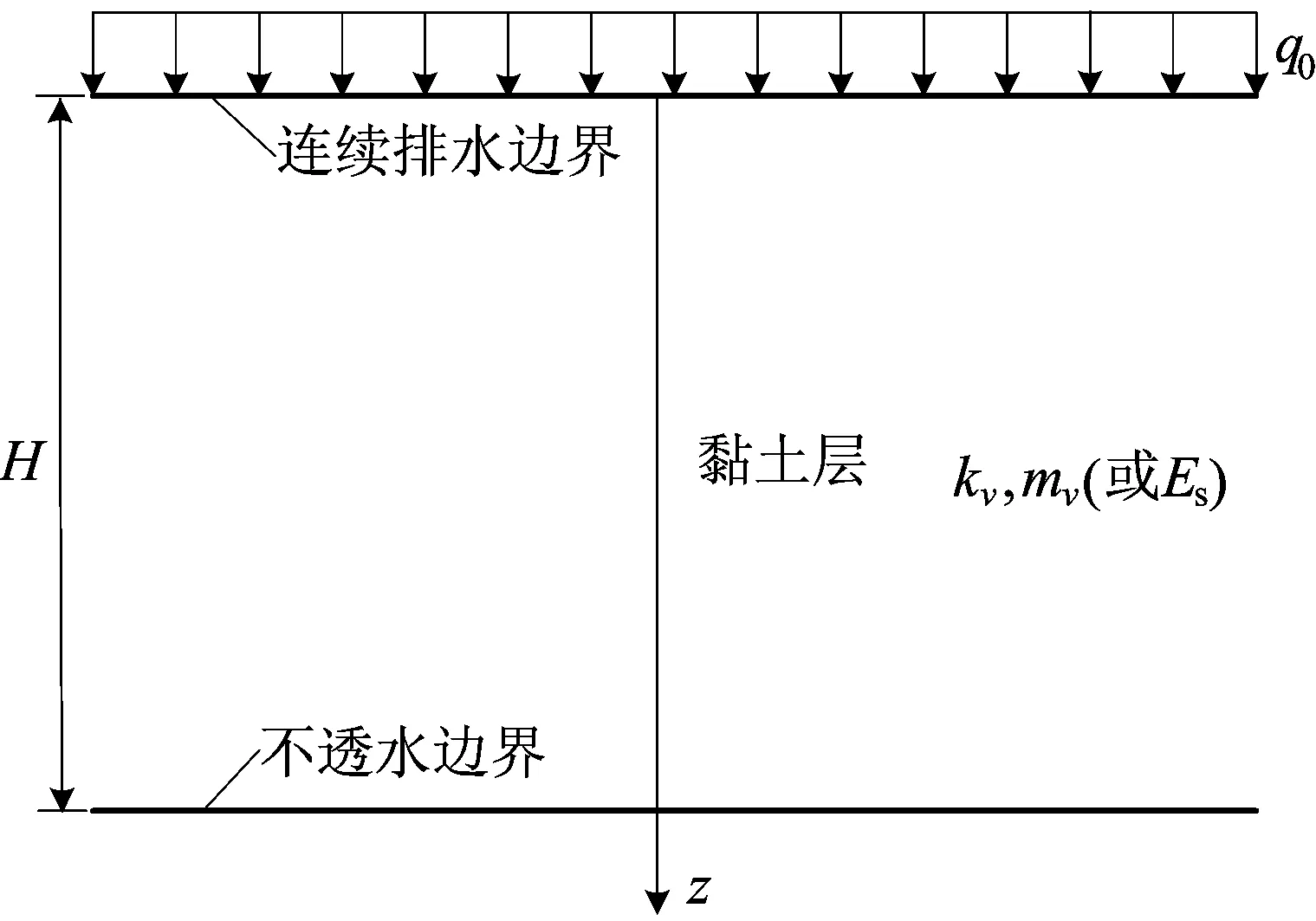
图1 软土地基一维固结模型
无限均布荷载q0施加于均质黏土层表面,黏土层厚度为H。考虑到起始水力坡降i0的存在,渗流模型[14]为:
(1)
其中:i为水力坡降;kv为黏土层的渗透系数;v为黏土层中水的流速。除边界条件和渗流模型外,采用与Terzaghi一维固结理论相同的基本假定,考虑起始水力坡降,得到软土移动边界以上土体的一维固结控制方程[20]为:
(2)
其中:cv为土体的固结系数;u为土中的超静孔压;t为固结时间;z为深度。
1.2 固结模型的定解条件
土层顶面是随时间指数变化的变排水边界,该变边界处超静孔压为:
u(0,t)=q0e-b t
(3)
其中,b为界面排水系数,其值反映土体的排水能力,可通过实验反演得到,其值越大,边界排水性越好。
起始水力坡降致使排水固结过程中存在着渗流移动边界,土层底面是不透水边界,若移动边界到达土层底面,则不透水边界处孔压为:
(4)
其中,γw为水的重度。若移动边界未到达土层底面,记t时刻移动边界到透水面的距离为h,则渗流锋面即z=h处,u、i应满足的边界条件为:
u(h,t)=q0
(5)
(6)
2 单面排水下模型数值解
2.1 控制方程无量纲化
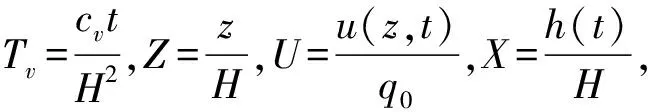
(7)
固结模型边界条件采用无量纲变量表示为:
(8)
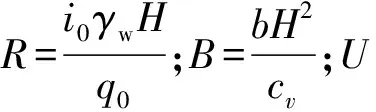
2.2 差分方程的建立与求解
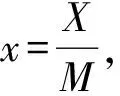
(9)
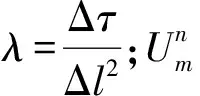
(10)
(11)
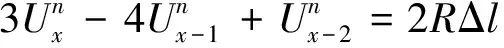
(12)
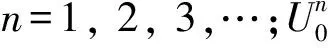
(13)
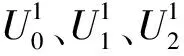
求解(13)式可得到第1时段的时间间隔T2。在此基础上,可利用(9)~(12)式计算渗流前锋以上土层中的超静孔压。
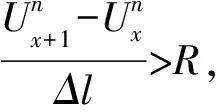
(14)
(15)
(16)
3 差分解的验证
为了验证本文差分解的可靠性,将本文差分解与已有的特殊情况下解析解作对比分析。
3.1 与考虑i0的完全透水边界对比
b的取值大小反映本文模型的边界透水性能,b越大,土层排水面的透水能力越强。令b取无穷大值(B→∞),则变边界可以退化为完全透水边界。文献[20]给出了完全透水边界下考虑i0的软土一维固结解析解。
取M=100,Δτ=10-5,B=105,利用本文差分解计算R为0.2、1.2时的移动边界及超静孔压随时间变化的曲线,同时利用文献[20]解析解进行计算,结果如图2所示。
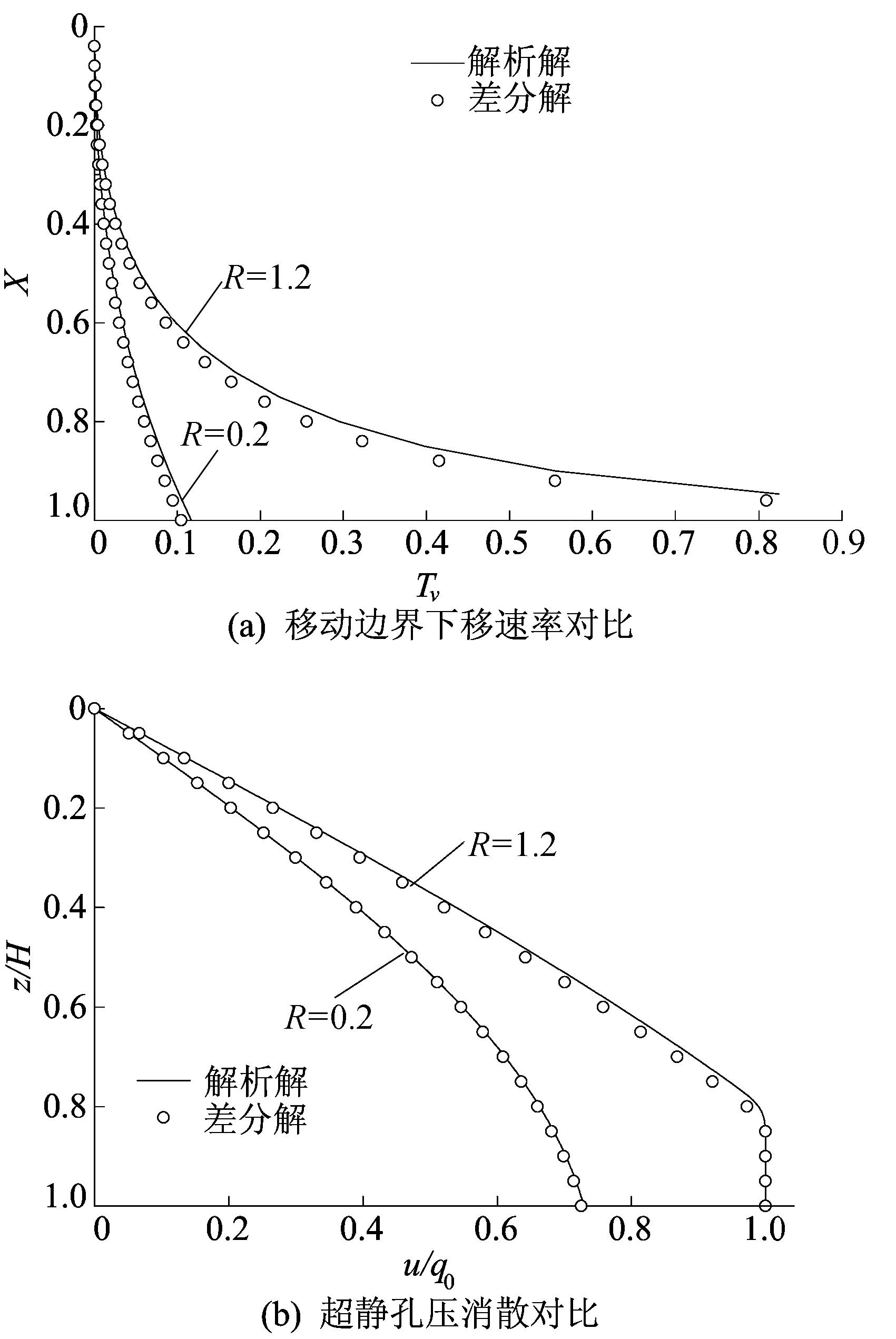
图2 B=105时差分解与解析解的对比
从图2可以看出,差分解与解析解非常接近,存在稍许偏差是由于差分解自身精度的影响,以及文献[20]的解析解本身仅是近似解析解。
3.2 与Darcy定律下变排水边界对比
考虑i0的渗流模型当i0=0时即退化为Darcy渗流模型。令差分解中的i0趋近于0(R→0),将考虑i0的渗流模型计算结果与Darcy定律下变边界的固结解析解进行对比分析,进一步验证本文差分解的可靠性。文献[2]中Darcy渗流单面排水下变边界的固结解析解与本文差分解对比如图3所示。
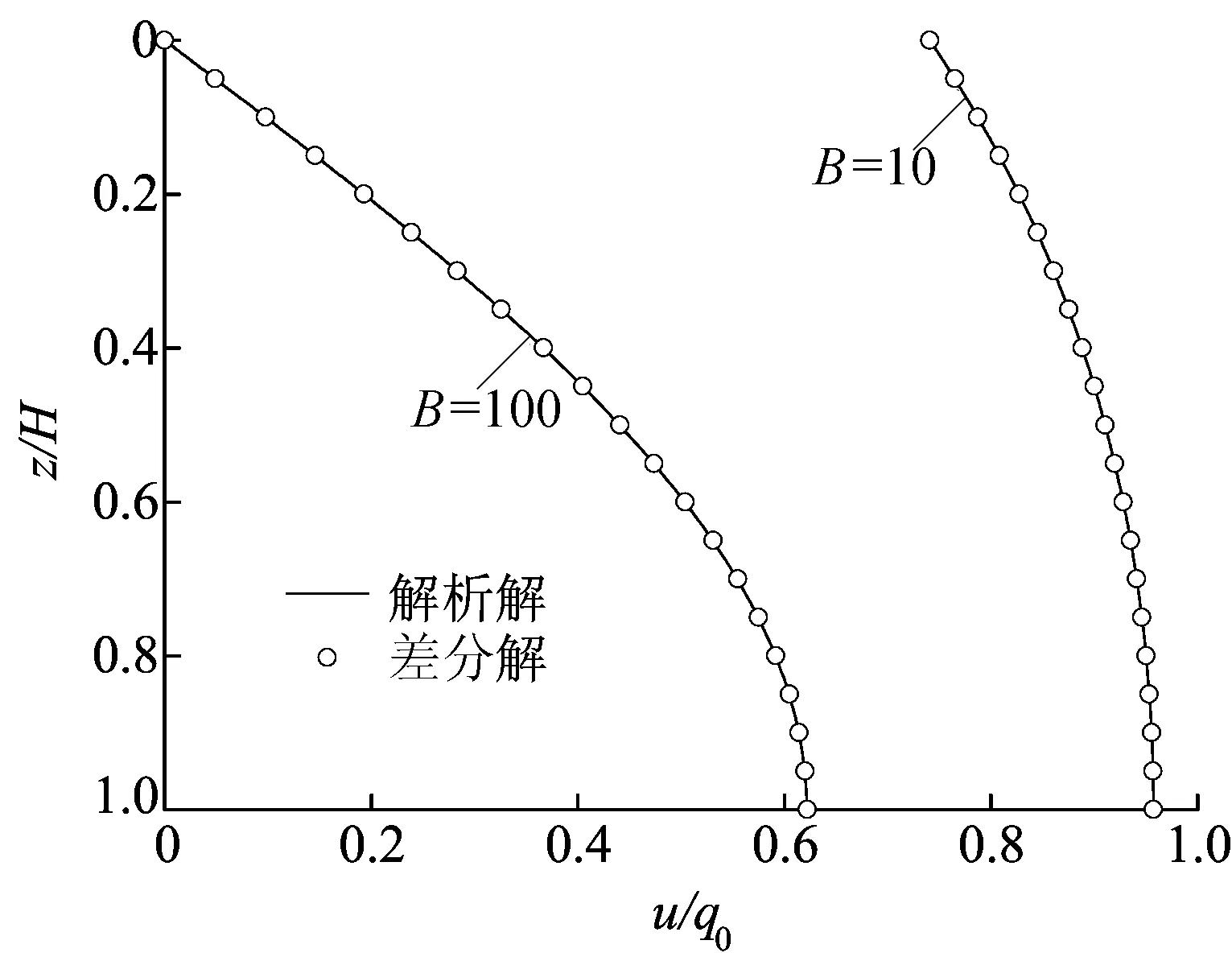
图3 i0=10-5时差分解与Darcy定律下解析解的超静孔压对比
从图3可以看出,当i0取值很小时,本文考虑i0的差分解与Darcy定律下考虑变边界的解析解结果一致,这进一步说明了本文差分解的可靠性。
4 固结性状分析
本文固结模型的主要影响因素为起始水力坡降和随时间改变的排水边界。
计算模型参数取值见表1所列。
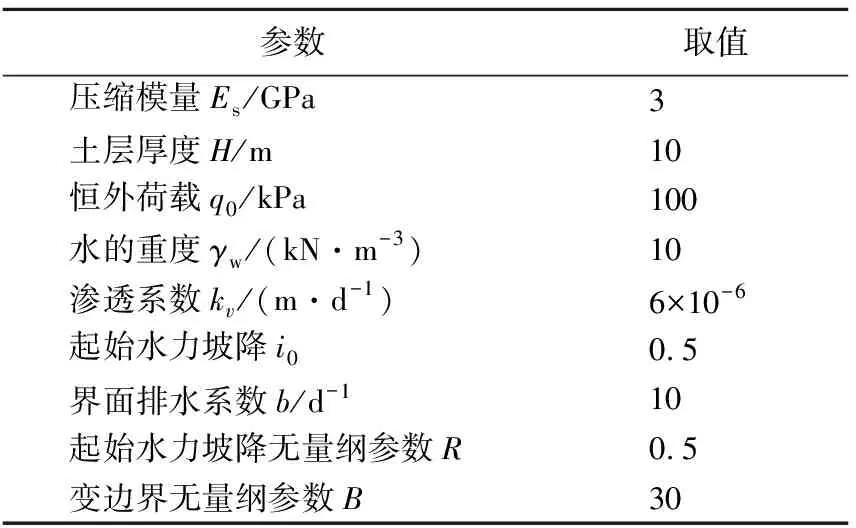
表1 计算模型参数取值
下面重点讨论考虑起始水力坡降与Darcy渗流下固结性状之间的差异,以及变排水边界下与完全透水边界下固结性状之间的差异,分析起始水力坡降、排水面透水性对固结性状的影响。
4.1 R对固结性状的影响

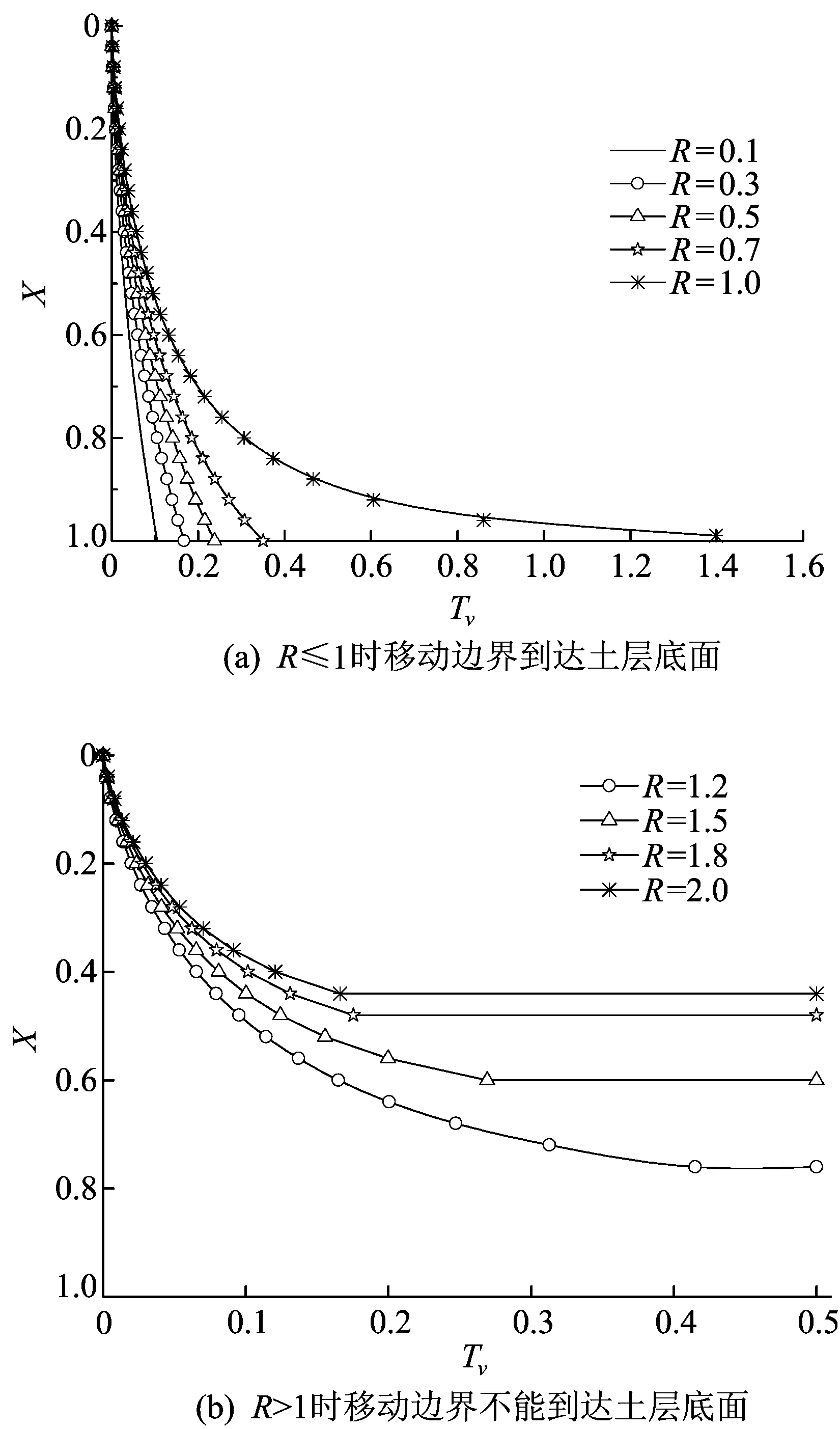
图4 R对移动边界的影响
超静孔压随时间和深度的消散曲线如图5所示。从图5a可以看出:Darcy定律下(R=0)软土地基的超静孔压随时间消散最快,且其最终能完全消散至0;但R≠0时,土中超静孔压即使在固结完成后仍不会完全消散;随着R取值增大,相同时刻的超静孔压也不断增大,且固结完成时的超静孔压残留值也不断增大。从图5b可以看出,相同深度处超静孔压随着R值增大而增大,超静孔压的最终残留值也不断增大。
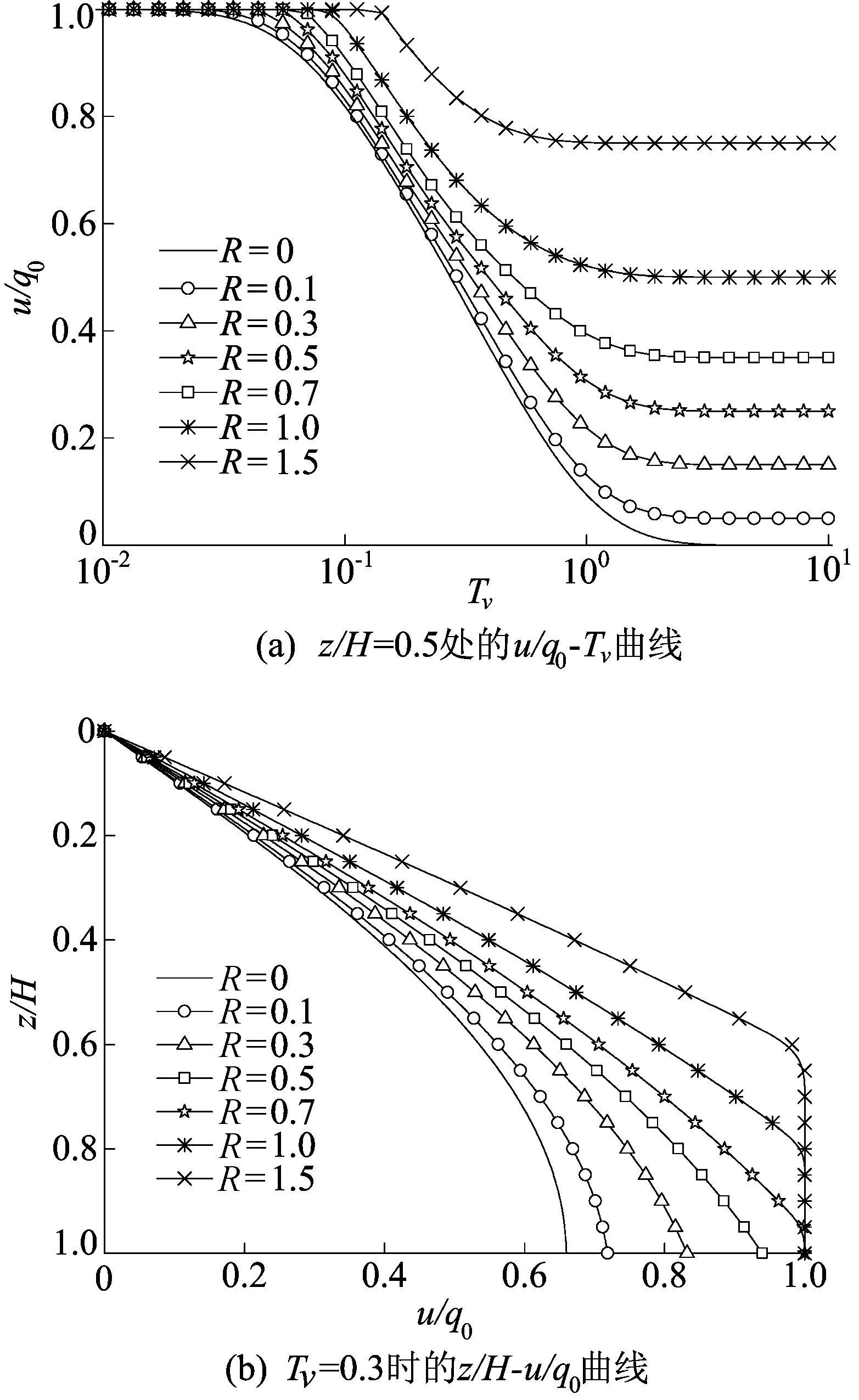
图5 R对超静孔压消散的影响
不同R值下土层平均固结度Up与Tv的关系曲线如图6所示。当R=0时变排水边界下Up最终能达到100%,且相同Tv下其Up最大。由于i0的存在,超静孔压不会完全消散,Up不能达到100%,但超静孔压达到稳定值所需的时间随R值增大而变短。
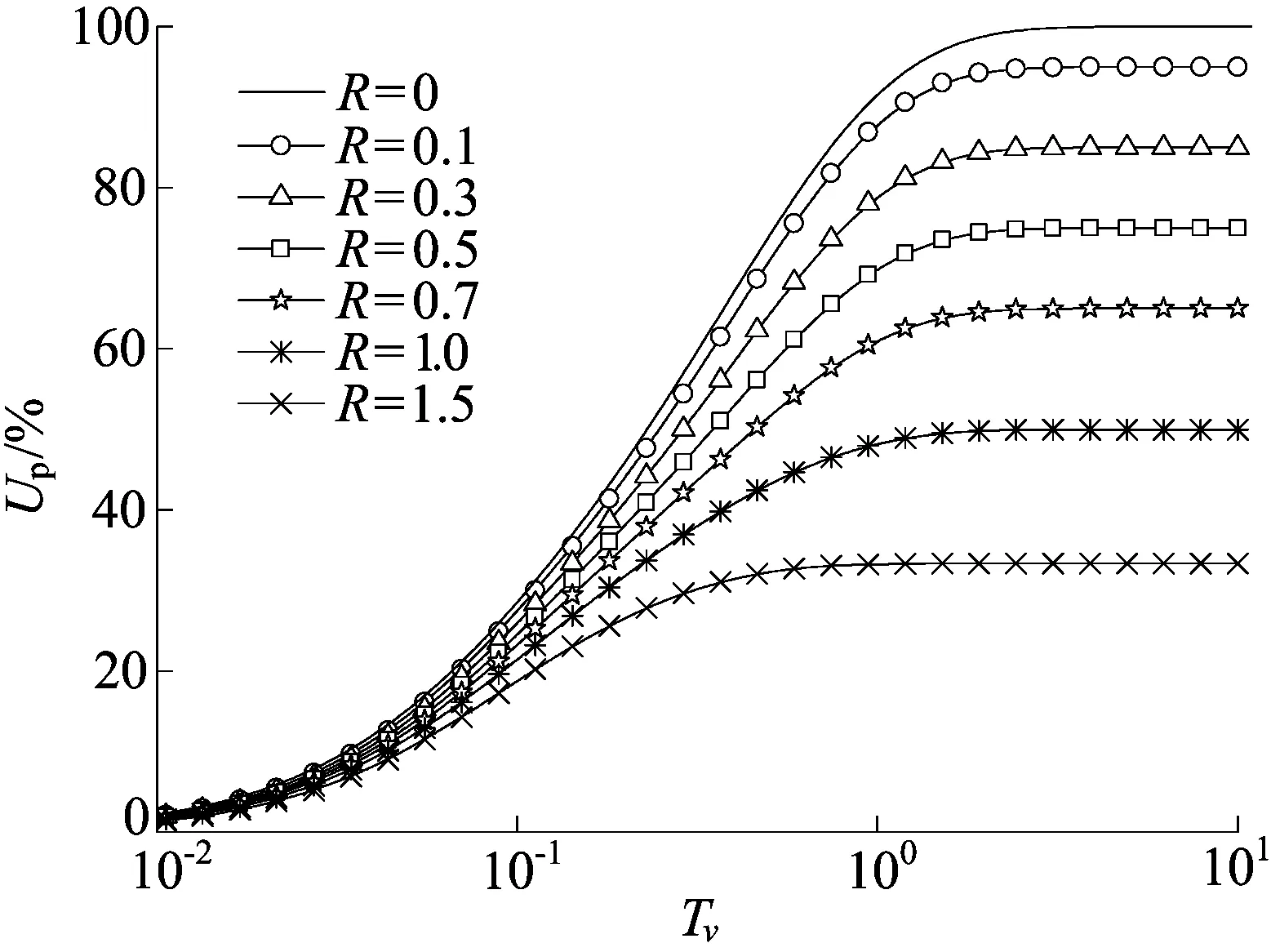
图6 R对固结度的影响
4.2 B对固结性状的影响
具有不同排水能力的变边界下渗流前锋随时间的下移曲线如图7所示。B值代表透水边界透水能力随时间的变化程度,在不同排水边界下,移动边界随时间的下移曲线各不相同,这说明边界条件对超静孔压的消散过程影响较大,B越大,移动边界到达底部的时间越短。
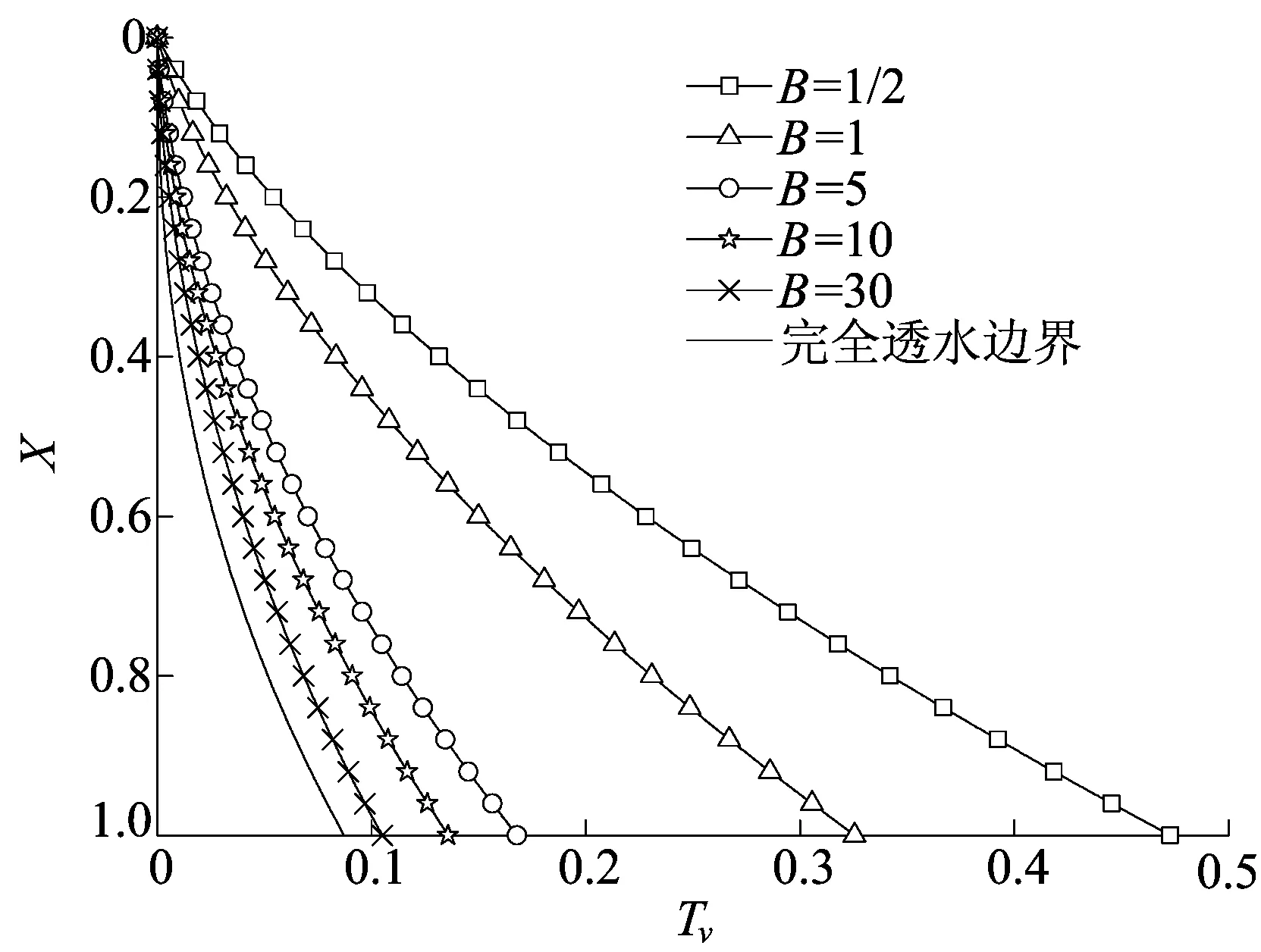
图7 B对移动边界的影响
关于移动边界的固结性状,可从z/H=0.5处超静孔压随时间消散过程进一步得到验证。B对超静孔压消散的影响如图8所示。
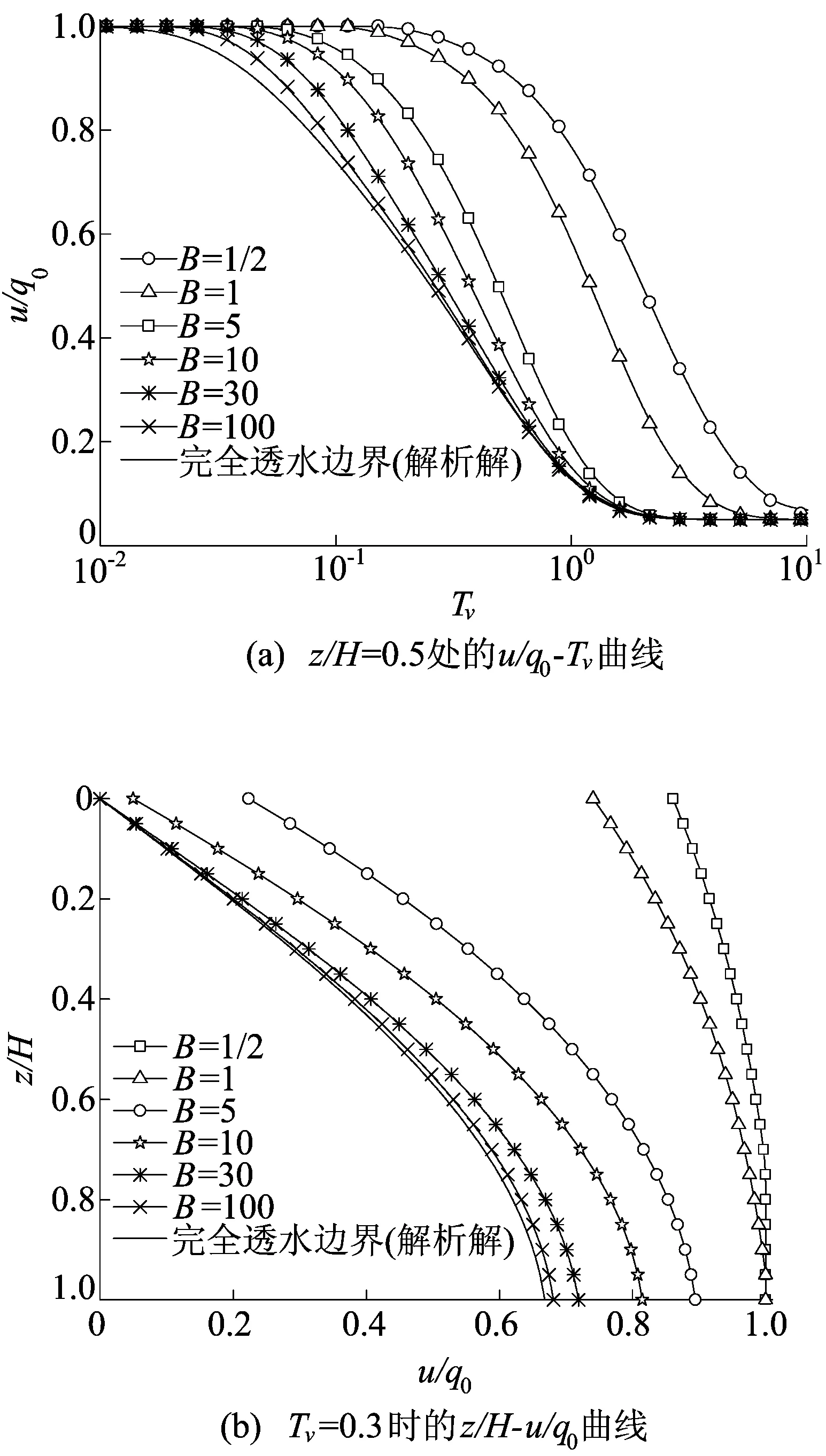
图8 B对超静孔压消散的影响
从图8a可以看出:z/H=0.5处的超静孔压开始消散的时间各不相同,B值越大,超静孔压开始消散的时间越短,且其消散曲线越接近完全透水边界的消散曲线;相同时间下完全透水边界下z/H=0.5处超静孔压最小,但由于具有相同的R值,该点处的最终超静孔压均到达相同值。
从图8b可以看出:相同深度处完全透水边界下超静孔压值最小;随着B值减小,相同深度处的超静孔压值逐渐增大;B值越大,超静孔压沿深度分布曲线越接近于完全排水边界下的分布曲线。
上述超静孔压消散的特征可进一步在固结度曲线中得到验证。超静孔压消散速率越快,Up越大。
B对土层平均固结度Up的影响如图9所示。从图9可以看出,相同时间下B值越大,Up越大,越接近于完全透水边界下的固结度曲线。这样的固结性状完全与超静孔压消散表现出的固结性状一致。
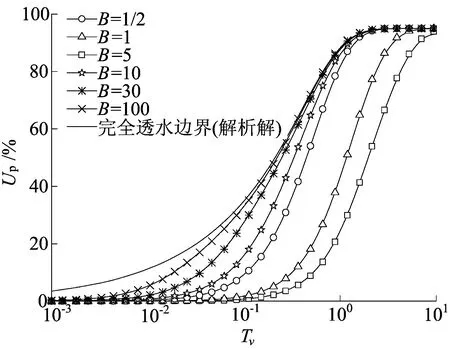
图9 B对土层平均固结度的影响
5 结 论
(1)本文给出同时考虑变排水边界和起始水力坡降的软土一维固结数值解,为实际考虑上述影响的软土固结计算提供了可供参考的方法。
(2)考虑随时间变化的变边界与完全透水边界相比,土层中的超静孔压消散速率和土层的固结速率均会明显降低,边界透水能力越强,固结曲线越接近于完全透水边界下的固结曲线。
(3)变边界下起始水力坡降对固结性状的影响与完全透水边界相比,并未发生根本性改变,只是固结速率进一步变缓。
