预应力锚索格构梁工作阶段格构内力计算方法

俞美华 宁万辉

(1.湖北地环岩土工程有限公司，湖北 荆州 434000； 2.中国铁路武汉局集团有限公司宜昌综合维修段，湖北 宜昌 443000)

1 概述

在预应力锚索格构梁体系中,格构梁除了表层加固作用以外,还起到传力作用。在单独使用预应力锚索进行边坡加固时,有时会因为坡体过大变形导致锚索预应力损失。将预应力锚索与格构梁相结合,格构梁起到锚墩的作用,由于格构梁与坡面的有效接触面积大,坡体在锚索作用下其变形受到限制。因此,预应力锚索格构梁的内力计算时应该考虑锚索对格构梁的影响。

2 格构梁计算模型的建立

在工作阶段,滑体或者坡体下滑或者有下滑的趋势,岩土体的下滑力作用在格构梁上,格构梁作为传力体系将岩土体下滑力传递给锚索,锚索通过自由段、锚固段将岩土体的下滑力传给稳定的岩层。锚索因其自身材料特性,受到格构梁传递的岩土体下滑力之后会发生拉伸变形,变形值主要与锚索的自由段长度、锚索的弹性模量、锚索的截面面积有关,与这三个因素有关的系数称为锚索的柔度系数Ci。

锚索简化为作用在格构梁上的弹性支座,格构梁作为固定在弹性支座的连续梁,受力体系的基本结构为多跨的弹性支座上的连续梁,锚索的柔度系数Ci可表达为式(1)[1]:

(1)

其中，hi为第i根锚索的自由段长度;EiAi为第i根锚索的自由段截面刚度。

将格构梁、锚索、岩土体共同作用的组合体系简化为图1所示模型,锚索在拉力的作用下会发生拉伸变形,将锚索简化为作用在格构梁上的弹性支座。锚索的柔度系数Ci等价于弹性支座的弹性系数。两锚索之间的距离为一跨,每跨的跨距根据实际工程而定。

3 内力计算方法

格构梁作为固定在弹性支座的连续梁,格构梁上作用有岩土体下滑力,图2为弹性支座上连续梁的计算简图。影响作用在格构梁上的岩土体下滑力的分布形式的因素较多,有关推力的分布形式,目前比较常用的有三角形、矩形、梯形三种,滑坡推力的分布对格构梁的内力计算影响较大,尤其是对于滑坡推力比较大的滑坡。根据国内所做的模型试验可知[2-4],滑坡推力对于那些具有一定沉积年代且具有一定胶结的滑体,三角形和四边形分布都不尽合适,近似的梯形分布应该是比较符合实际的[5]。

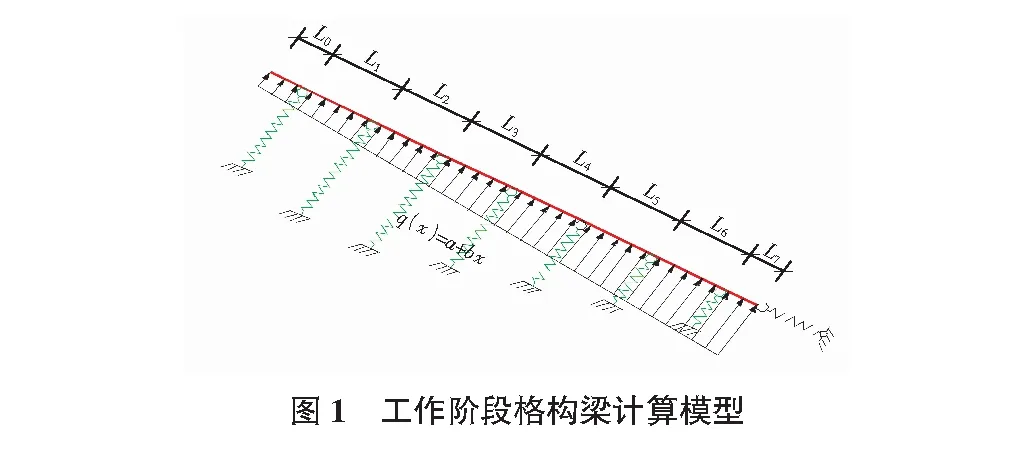
工作阶段格构梁计算模型中仅考虑垂直于格构梁的岩土体下滑力分力,不考虑与格构梁平行的下滑力分力,在工程中通常格构梁各跨的变形模量E基本相同,取各支座处的弯矩为多余未知力,则基本结构为多跨的弹性支座上的简支梁,如图3所示。

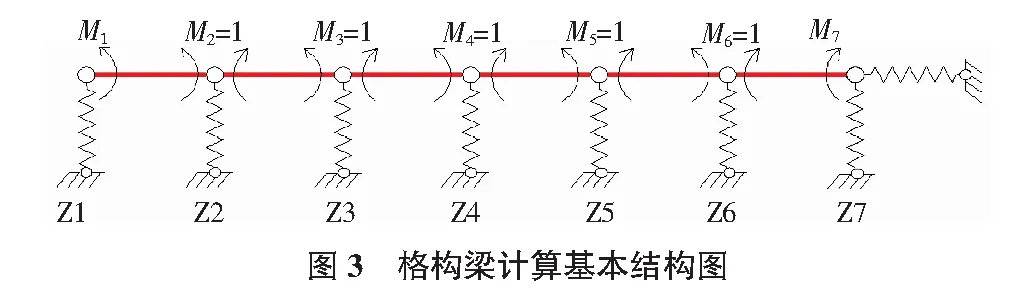
超静定结构的内力计算方程(式(2))为:

(2)

由于考虑了弹性支座的变形,上式中的系数较固定支座复杂,在图4a)～图4e)中，绘出了基本结构在单位基本未知力作用下的单位弯矩图及弹性支座的支承反力图。

从图4a)～图4e)可知上式中的系数δij不但要考虑弯矩作用的影响同时要考虑到弹性支座轴力的影响。系数δij表达式为:

。

从图2格构梁计算简图可知,格构梁悬臂段同样受到线性分布的岩土体下滑力作用,在作基本结构弯矩图前,将基本结构上的荷载简化为图5所示,自由项的确定于采用固定支座的连续梁相比较,采用弹性支座时也要考虑支座的变形。

综合图5和图4的自由项系数为:

。

将系数和自由项代入内力计算方程即可进行内力求解。

4 结语

在工作阶段锚索的长度、截面面积、材料不同,锚索的柔度系数Ci也不尽相同。边坡岩土体在预应力锚索格构梁工作阶段的潜在变形产生的下滑力视为线性分布力,锚索作为弹性支座,将格构梁视为作用在弹性支座联系梁。采用上述计算方法计算出格构梁内力与锚索张拉阶段计算出的格构梁内力进行比较,绘制内力包络图,得到最不利内力组合,从而为格构梁的设计提供计算依据。