开放系统悬臂类结构的动力特性计算方法

付相球，潘旦光,2

(1. 北京科技大学土木工程系，北京 100083；2. 城市地下空间工程北京市重点实验室，北京科技大学，北京 100083)

结构动力特性主要包括自振频率、阻尼比和振型，是评价结构动力反应、抗震性能、损伤状态的重要指标，被广泛应用于结构地震反应分析、震害评估、健康检测等结构工程领域。真实结构总是建立在场地之上，土-结构间存在相互作用，彼此形成具有能量传递的开放系统。研究[1−3]表明，相比于刚性基础假定的封闭系统，场地条件降低了结构的频率，增大了结构的阻尼。准确地计算结构动力特性，是结构抗震设计的基础[4−5]，但考虑土-结构相互作用开放系统的结构动力特性的计算依然存在不少问题。

由于地基刚度计算的困难性和随频率变化的复杂性，以及地基的无限性，导致人们不得不寻求简便方法来等效真实的开放系统。对于均质条件下的弹性半空间，如果不考虑地基土的动力效应，即可直接用地基静刚度进行简化计算[6]，这种方法忽略了地基土的阻尼效应和附加质量而导致地震反应误差较大。为考虑辐射阻尼等效应，可利用解析解形成阻抗函数，因阻抗函数与频率相关难以在时域中进行计算，由此提出了频率无关的集总参数模型[7−9]。李昌平等[10]基于集总参数SR 模型，推导了简化隔震结构模型动力特性参数表达式；王满生和潘旦光[11]基于双自由度集总参数模型，研究了不同土层对上部结构动力特性的影响；王国波等[12]分别采用Veletsos 和Richart 经验公式对一个简单的3 层框架结构计算地基的阻抗值，并以此为基础对框架结构进行模态分析。SHI[13]针对层状土层地基且考虑平动和转动的耦合项，提出一种系统地生成集总参数模型的方法。KECHIDI 等[14]基于4 参数集总参数模型考虑辐射阻尼的影响，提出一种可直接应用于OpenSees 的基于性能的抗震设计方法。集总参数模型计算简单，易于操作，但地基阻抗函数是基于有限频率范围下的均质土层得到，因此该方法计算精度有限且难以模拟复杂的结构和场地。

随着数值计算的发展，截取有限范围的土-结构相互作用有限元模型，其地震反应分析计算精度高，且可考虑各种复杂因素而得到广泛的应用[15−17]，但对直接有限元模型进行模态分析时，存在土体范围和人工边界的选取缺乏统一性、结构模态识别工作量大的问题。鲍华等[18]对一基础隔震的框架结构截取了不同深度、半径为上部结构5 倍的圆柱土体模型，模型底部固定，四周竖向约束，得到结构自振周期随着土体深度的增大而增大的结论。潘旦光等[19]在结构-土-结构相互作用的动力特性研究中，计算模型的侧向采用了自由边界，底部固定，土体宽度取了8 倍基础宽度，研究了结构与土体的频率比、基础宽度与土体厚度的宽厚比对结构自振频率的影响。李海山等[20]对一网壳结构截取了20 m 深度、5 倍于柱壳平面尺寸的土体，采用等效粘弹性边界单元，与刚性基础下的结构动力特性计算结果相比，体系基频从1.869 Hz 降低到了0.565 Hz，且体系振型发生明显改变。然而，一方面，振动台实验结果显示，就算是软土场地对结构自振频率的降低效果也不会如此明显[21−23]；另一方面，由现场模态实验结果可知，建立在真实场地之上的结构具有稳定可测的模态[24−27]。理论上，数值模型的土域范围增大时其模拟效果应该更好，这与随土体范围增大体系基频不断降低直至收敛到零相矛盾。这是因为，对整体有限元模型直接进行模态分析时，计算结果为土-结构系统的动力特性，而非结构本身的动力特性，因此不同土体范围和人工边界下的模态分析结果完全不同，当土体单元较多时，还需从成千上万个系统模态中挑选出相应的结构振动模态。荣峰等[28]取深度范围60 m、水平方向范围为3 倍双塔高层建筑横向尺寸的地基，采用粘弹性人工边界直接模态分析，结果显示，有限元模型所涉及的频率范围很宽、频率变化缓慢，很多模态都是场地土局部振动模态，前180 阶模态中只有4 个模态是以上部结构振动为主，只能人为选取这4 个模态作为结构的前四阶模态。潘旦光等[29]也曾对SSI 体系进行缩尺模型实验和原型有限元分析，由于土体单元较多，有限元模态分析结果存在上万阶模态，只能从中匹配出相应的结构振动模态，这也给开放体系下结构动力特性的计算带来了很大的困难。由此可知，因为直接有限元法得到的是系统的模态，为考虑半无限地基的辐射阻尼，当有限元模型采用粘性人工边界时，此时体系存在刚体模态而导致基频为0，对于粘弹性人工边界则随着土域范围增大收敛至0；同时，模态分析结果中存在大量土域的模态，需要从中识别结构的振动模态，但目前还没有明确的识别方法。

既然土-结构有限元模型可以有效地进行开放系统的土-结构相互作用地震反应分析，而结构的动力特性实际上体现的是结构在自由振动时表现的固有特点，因此完全可以通过某种方式激发结构的自由振动，由此识别结构的动力特性。真实建筑结构的现场模态试验常利用大地脉动激励近似白噪声的特点，采用未知输入下的模态识别方法得到包括土-结构相互作用效应的动力特性[30−33]。但从识别试验结果看，采用已知输入的模态识别方法的精度更高，实际工程结构采用无输入下的模态识别是由于对工程结构施加激励比较困难。但是，受这个试验方法启发，在开放体系动力特性的数值计算时，人为地施加一个脉冲信号，测量结构的动力反应，由此采用模态识别的方法计算开放系统下结构的动力特性。该方法首先建立土-结构相互作用开放系统的直接有限元模型，通过对结构施加脉冲荷载激发结构的自由振动反应，然后由实验模态分析方法识别结构的动力特性。这种方法借助脉冲荷载下模态试验技术，形成土-结构相互作用体系动力特性的数值计算方法，因此，将这种方法称为脉冲荷载响应模态分析法。为验证所提方法的有效性，以一个半无限空间上的悬臂类5 层框架结构为例，研究了所提算法计算结构动力特性的收敛性，并分析了脉冲荷载激励点位置和土材料阻尼对计算结果的影响。在此基础上，讨论集总参数法、直接模态分析法和本文方法计算结果的差异。

1 脉冲荷载响应模态分析法计算理论

对于图1 所示建立在半无限空间土域上的结构，为分析开放系统下结构的动力特性，截取有限土体，施加粘弹性人工边界用以模拟波的辐射效应，建立二维土-结构相互作用直接有限元模型如图2 所示。采用脉冲荷载激发结构的自由振动反应时，根据激励点的多少可分为单输入多输出与多输入多输出2 类。不失一般性，本文以多输入多输出为例介绍所提方法的理论计算过程，单输入多输出方法作为一种特殊情况同样适用。nf个脉冲荷载输入下，有限元模型离散为n自由度体系的运动方程为：

图1 半无限空间土域上的结构Fig. 1 A structure on soil of semi-infinite space

图2 二维土-结构有限元模型Fig. 2 2-D finite element model of soil-structure interaction

将脉冲荷载称为输入，体系的动力响应称为输出。已知输入和输出，即可采用模态识别方法进行结构的动力特性的计算。本文以特征系统实现算法(ERA)[34]为例，讨论已知脉冲荷载信号和结构动力反应信号下模态参数的计算问题。采用状态空间法进行式(1)的求解[35]，即：

式中：abs 为取绝对值；real 为取实部。

上述即为脉冲荷载响应模态分析法的整体计算过程，不同于传统的实验模态分析方法，所提方法的“实验过程”通过数值模拟完成，“实验数据”来自于数值模型的动力计算结果，该方法结合了数值计算方便、计算精度高和试验模态分析可直接得到结构部分的动力特性的优点，从而形成土-结构相互作用开放系统结构部分动力特性的计算方法。避免了整体有限元模型直接模态分析方法人为选择结构振动模态的过程，直接得到结构的各阶振型。

2 开放系统结构动力特性的收敛性

2.1 土-结构相互作用直接有限元模型

以一个半无限空间土域上的悬臂类5 层框架结构为例，框架的长度远大于宽度，由此取其中一榀将结构简化为平面问题进行分析，已知基础宽度b=12 m，厚度h=1 m，密度为 ρb=2700 kg/m3，弹性模量Eb=30 GPa，泊松比μb=0.3；上部框架结构简化为集中质量模型，各层的等效质量和侧移刚度见表1。弹性半空间土域采用均质弹性土体，考虑到场地土体类型不同，土体的剪切波速不同。为此，以表2 所列5 种不同剪切波速讨论土体波速对结构动力特性的影响。这部分内容为研究辐射阻尼效应导致的结构各模态阻尼比，因此计算过程不考虑结构、基础和土体的材料阻尼。

表1 五层结构水平方向等效质量、刚度Table 1 Horizontal equivalent masses and stiffnesses of a 5-story struture

表2 不同波速土体参数Table 2 Soil parameters of different wave velocities

地基土采用半圆形土体模型，其中r=50 m 时的有限元模型如图3 所示，土体与基础均采用平面四边形等参单元，悬臂结构采用集中质量模型，质量采用集中质量单元，层间刚度采用约束转动自由度的梁单元模拟，土体的人工边界采用粘弹性边界，由弹簧单元模拟，弹簧的刚度系数和阻尼系数取为[38]：

图3 土域半径r=50 m 时土-结构有限元模型Fig. 3 Finite element model of soil radius r=50 m

式中：A0为脉冲荷载幅值，本算例取为1000 kN；B0控制脉冲段的持时，取1000；t0为脉冲中心时刻，取为2 s；为保证计算精度，时间步取为0.01 s，总时长为20.48 s，时程和傅里叶谱如图4 所示。

图4 脉冲荷载Fig. 4 Impulse load

2.2 计算结果分析

有限元模型建立后，由于悬臂类结构模型简单，因此采用单输入多输出的激励方式，在基础水平方向施加脉冲荷载，计算结构体系的水平位移反应。其中，土体剪切波速为200 m/s、土域半径r=50 m 时，计算得到结构底层与顶层的位移反应如图5 所示，从中可以看出结构在脉冲荷载激励后的自由振动衰减。

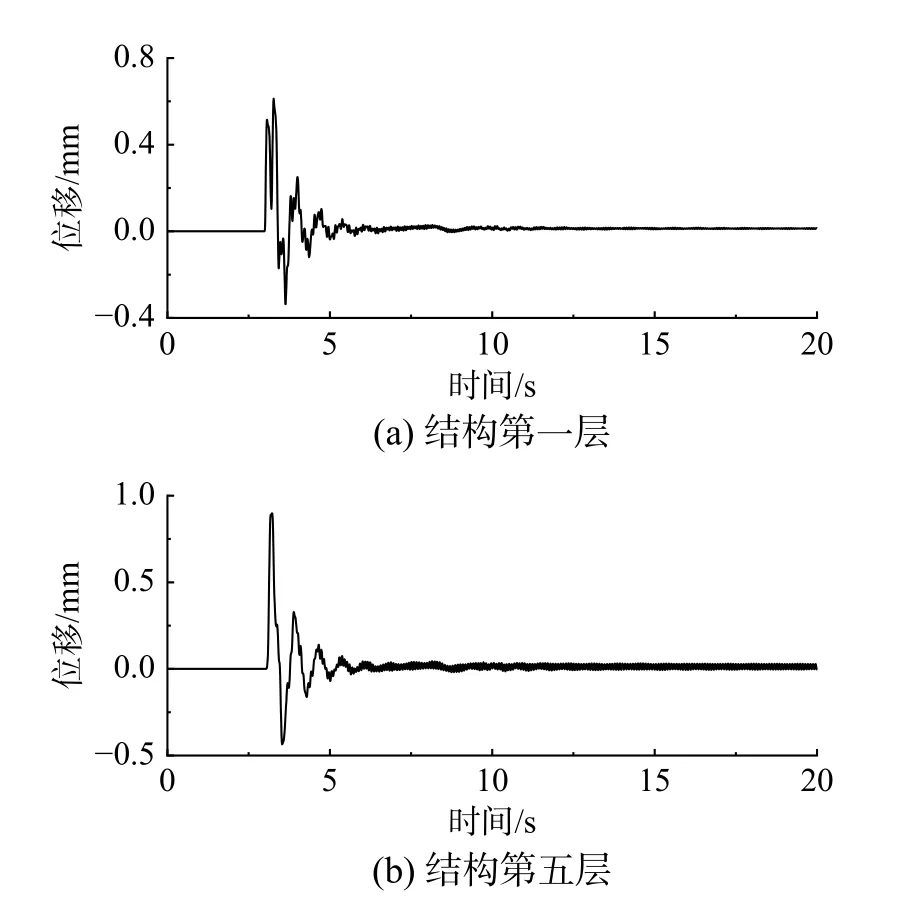
图5 结构水平位移时程Fig. 5 Time history of horizontal displacements of the structure

为研究开放系统结构动力特性的收敛性，对不同土域半径(r=20 m～1000 m)下的模型采用所提方法进行结构模态参数识别，得到不同剪切波速地基下结构前三阶自振频率与阻尼比随土域半径r的变化规律如图6 所示。由图6 可以看出：① 当截取的土域范围较小时，结构动力特性计算结果存在波动，这主要是由人工边界的反射效应引起的；② 随着计算土域半径r的增大，结构自振频率和阻尼比均收敛到稳定值，说明本文方法可以有效地计算开放系统下结构的动力特性；③ 随着地基土剪切波速增大，结构的各阶自振频率增大，阻尼比减小。

图6 不同剪切波速地基下结构动力特性随土域半径r 的变化Fig. 6 Structure dynamic characteristics under different soil radius rof different shear wave velocities of soil

式中， λ1为土体在刚性基础下结构基频对应的波长，简称基频波长。由此计算结构动力特性的相对误差随无量纲土域范围d的变化曲线(图7)。

由图7 可以看出：① 随着土域范围变大，结构自振频率与阻尼比相对误差的整体趋势变小；② 土域范围较小时结构阻尼比相对误差较大，当d≥2 时，各阶自振频率相对误差小于1%，各阶阻尼比相对误差小于5%。对于本文算例此类结构尺寸相对于土域范围较小的情况，以d≥2 作为截取有限土体范围的依据可取得较高精度的计算结果。此时，地基土剪切波速越大所需的计算土域范围越大，但同时单元尺寸也可相应地增大，因此不会增加额外的计算量。但对于大尺寸的结构，如水坝等大型公共设施，此时不能简单地作为点源问题考虑，土域范围应该根据实际情况适当增大。

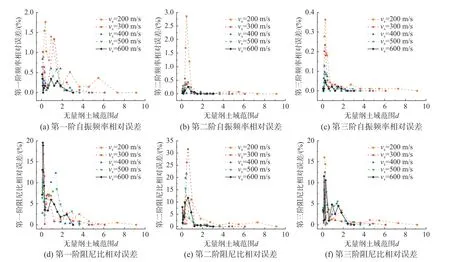
图7 不同剪切波速地基下结构动力特性相对误差随土域范围d 的变化Fig. 7 The relative errors of dynamic characteristics under different soil range dand different shear wave velocities of soil

除自振频率与阻尼比外，由式(13)可得结构的各阶振型。图8 为土体剪切波速200 m/s 下，r=400 m 时关于第五层幅值归一的结构前五阶振型。由于计算模型不包括材料阻尼，振型存在实部和虚部，表明由于土体辐射阻尼的存在，使得结构呈现了非比例阻尼的特征，与无阻尼或比例阻尼体系不同，此时各自由度振型幅值不会同时到达峰值点。

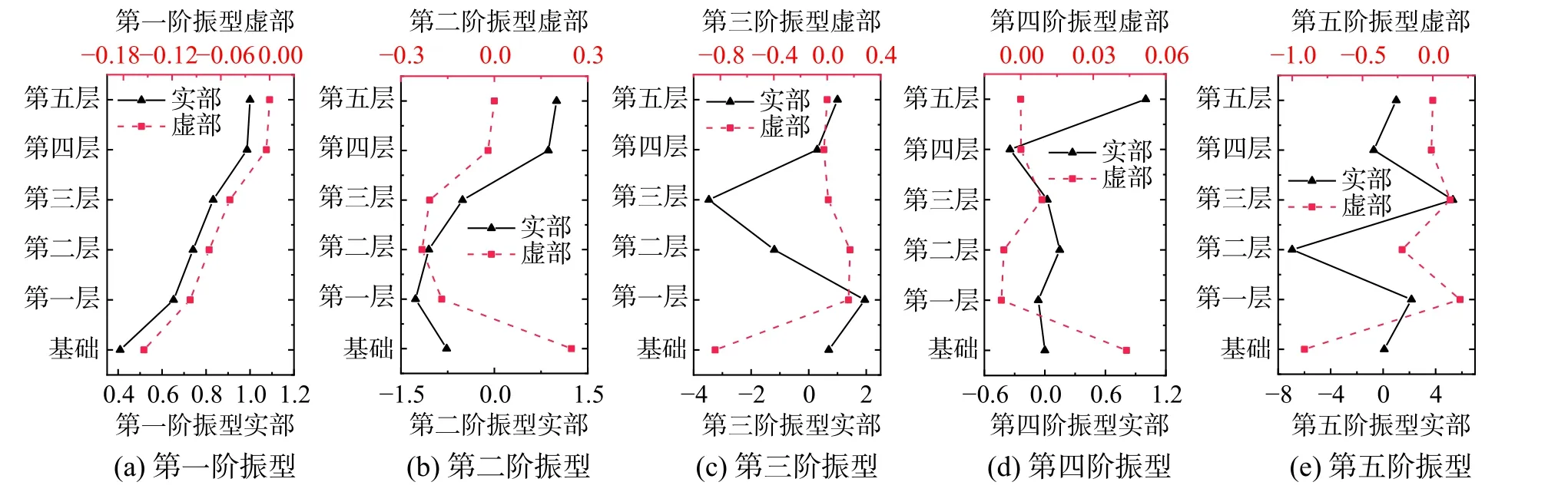
图8 所提方法计算的结构五阶振型示意图Fig. 8 The five modes of the structure calculated by the proposed method

2.3 不同激励点位置的影响

在锤击法进行试验模态分析时，激励点应避开重要模态的节点。脉冲荷载响应模态分析法从原理上看与锤击法相同，分析由脉冲荷载位置对模态分析的影响。为此，以基础、1 层～5 层分别作为激励点进行单输入多输出计算以及对结构所有自由度分别进行激励，采用多输入多输出方法计算，识别结构自振频率、模态阻尼比结果如表3、表4 所示。计算采用的模型为土域范围r=400 m、土体剪切波速200 m/s。

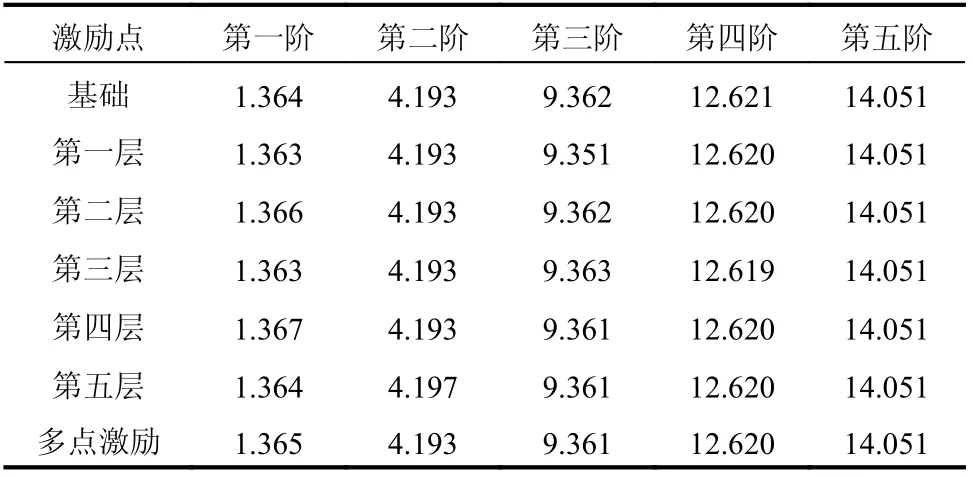
表3 结构前五阶自振频率/HzTable 3 The first five-order frequencies of the structure

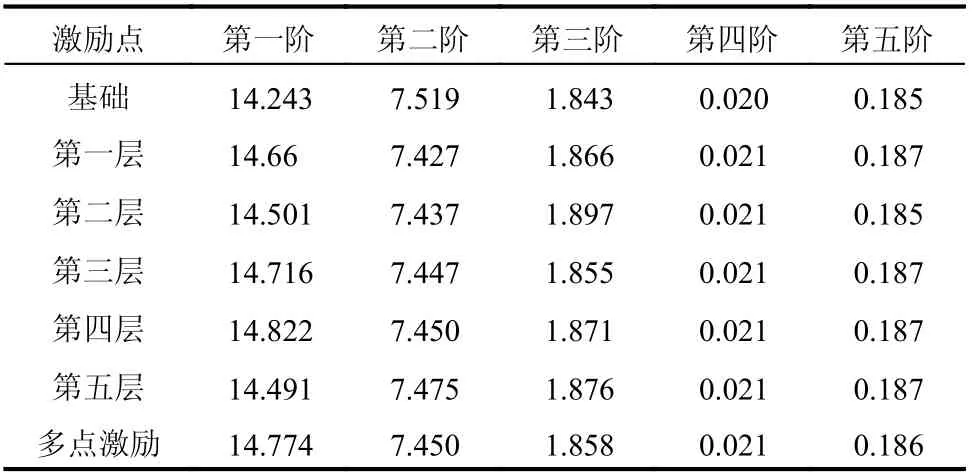
表4 结构前五阶阻尼比/(%)Table 4 The first five-order damping ratios of the structure

计算结果表明，不同激励点对结构动力特性的识别影响很小，自振频率差异在1%以内，阻尼比差异在5%以内。这是由于算例中集中质量位置都不是模态节点，数值计算的精度高，任一集中质量位置作为激振点都可激发结构各阶模态的自由振动，因而不会影响识别效果。为避免质量和刚度非均匀情况，部分模态和集中质量位置重合问题，对于悬臂类结构建议以悬臂端或基础位置作为激励位置。

2.4 土体材料阻尼的影响

为考虑土体材料阻尼对结构动力特性的影响，采用瑞利阻尼构造土的阻尼矩阵，其中土的阻尼比取0.05，参考频率取结构的前两阶自振频率。阻尼的存在将引起振动的衰减，在相同的计算精度下，土体有材料阻尼的计算范围必然小于无阻尼的。因此，对于200 m/s、300 m/s、400 m/s、500 m/s 和600 m/s 剪切波速下土域计算范围，根据d≥2 分别取300 m、400 m、500 m、600 m和800 m。不同剪切波速下，考虑和不考虑土材料阻尼的结构各阶自振频率和模态阻尼比如图9 所示。

由图9 可以看出，不同波速土体下，与无阻尼土体相比，土体材料阻尼导致结构基频最大降低0.15%，第一阶模态阻尼比最大增加4.77%，这表明土的材料阻尼对结构的各阶自振频率几乎没有影响，对各阶模态阻尼比的影响远小于辐射阻尼，这与已有研究的结论[39]一致。

图9 不同剪切波速地基下结构各阶动力特性Fig. 9 Dynamic characteristics of structure under differentshear wave velocities of soil

3 不同方法计算结果对比

式 中 ：Kfc=πρs、Mfc=Kfc(b/vs)2、Cfc=Kfc(b/vs)为归一化因子；mf1、mf2、kf1、kf2、kf3、cf1、cf2、cf3取泊松比为0.33 时的值，分别为0.0013、0.347、2.085、−0.447、0.761、1.149、−0.509、1.194。直接模态分析分别进行了土体范围r=50 m、r=200 m 和r=400 m 下有限元模型的实模态分析，本文方法为土域半径取为400 m(d=3.7＞2)的计算结果。计算中土体的剪切波速取为200 m/s，不考虑土体和结构的材料阻尼。不同方法计算得到的结构前五阶自振频率和模态阻尼比分别见表5 和表6。

表5 结构前五阶自振频率 /HzTable 5 The first five-order frequencies of the structure

表6 结构前五阶阻尼比 /(%)Table 6 The first five-order damping ratios of the structure

由表5、表6 可以看出：① 刚性基础假定高估了结构的自振频率，结构基频相比于本文方法计算结果放大了34%，且无法考虑土体辐射阻尼的影响；② 整体有限元模型直接模态分析得到的前五阶频率随土域范围的增大而明显下降，400 m土域范围下模型基频已不足0.1 Hz，即模型基频随土域范围增大而趋向于0；这是因为直接模态分析方法计算的是土-结构相互作用系统的频率而不是结构的频率，当土域范围越大时系统频率越低，且该方法无法考虑辐射阻尼；③ 3 参数集总参数模型频率与阻尼比的计算结果与本文所提方法差别较大，8 参数集总参数模型的对于均质场地的自振频率和阻尼比的计算结果优于3 参数集总参数模型。但对于非均质场地情况下，集中参数模型建立比较困难，而本文所提方法采用有限元模型考虑土体，因此可适用于任意场地条件，因此，脉冲荷载响应模态分析法可计算任意场地条件下开放系统结构的自振频率、阻尼比及振型参数。

4 结论

为计算开放系统下结构的动力特性，提出脉冲荷载响应模态分析法计算悬臂类结构自振频率、阻尼比和振型。该方法在建立土-结构相互作用有限元模型的基础上，通过脉冲荷载激励得到结构动力反应，然后由模态识别方法计算结构的动力特性。根据理论分析和数值计算可得出以下结论：

(1) 随着开放系统截取土域范围的增加，不同土体剪切波速下结构的各阶自振频率与阻尼比计算结果均收敛到稳定值，当土域计算范围大于2 倍基频波长时，结构自振频率相对误差小于1%，阻尼比相对误差小于5%。

(2) 对于脉冲荷载响应模态分析法，采用任意非模态节点作为激励点都可以得到比较精确的结果。

(3) 土的材料阻尼对结构的各阶模态阻尼比有一定的影响，但远小于辐射阻尼对各阶模态的影响。

(4) 刚性基础高估了结构的自振频率，且无法考虑土体辐射阻尼的影响；3 参数集总参数模型计算误差很大，8 参数集总参数模型可用于均质场地的土-结构相互作用体系动力特性的计算；而整体有限元模型直接模态分析得到的基频是土-结构相互作用系统的基频，将随土域范围的增大而明显下降，且无法考虑土体辐射阻尼的影响。