基于RSM-GA 方法的超声振动切削工艺参数优化*

赵鹏程

（1.中国煤炭科工集团太原研究院有限公司，山西太原 030006;2.山西天地煤机装备有限公司，山西太原 030006;3.煤矿采掘机械装备国家工程实验室,山西太原 030006）

超声振动切削技术是指在切削加工过程中加入高频低振幅的复合加工方法[1]，此方法可提高刀具的使用寿命、提高工件加工精度，降低切削温度[2]，优点突出。由于具有鲜明的优势，超声振动切削加工可应用于难切削材料的加工、对表面质量要求较高的工件制作。但该技术在加工过程中存在着短板，比如，各工艺参数对工件加工质量的影响具有明显的不确定性，需要进行进一步的优化改进。

工件质量是评价超声振动切削工艺加工性能的一个重要指标，它与表面粗糙度直接相关，在其他因素不变的条件下，表面粗糙度越小，工件质量越好；表面粗糙度越大，工件加工误差越大、精度越小[3]。为了提高超声振动切削加工工艺性能，需要降低工件表面粗糙度。目前，超声振动加工工艺参数的优化问题，引起了行业内的普遍关注，很多研究者通过设计实验，利用遗传算法对参数进行优化改善。如吕东喜等人利用SPH算法进行参数优化[4]，陈海峰等人利用区域逼近求解算法优化超声磨削参数[5]，这类方法的局限性是容易造成部分最优，不能从全局的角度得到最优方案。此外，基于数学统计方法的优化分析也很普遍，如卢泽生等人用数值模拟法对精密超声切削进行优化[6]，张生芳等人用数值拟合方法优化几何参数等[7]，这类数学分析是很可靠的，但没有考虑到交互作用影响。综上所述，本文采用响应曲面法（RSM）与遗传算法相结合的方式，这种方法具有创新性，综合了上述实验方法和数学统计的准确性优势，又能反映出影响因子对于目标值的影响以及各参数间的交互作用[8]。

1 超声振动切削实验研究

1.1 实验材料与方法

本次实验材料选用45 钢，它的主要成分见表1，基本尺寸为ϕ50 mm×500 mm；试验在C6201 车床上进行，刀具材料为硬质合金YNG151C。

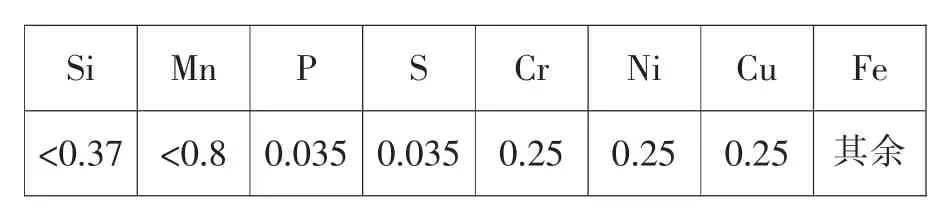
表1 45 钢的主要化学成分（质量分数，%）

实验装置示意图如图1 所示，接通电源后，超声波换能器产生超声振动，通过变幅杆放大振幅达成超声振动切削。我们用工件表面粗糙度（Ra）作为性能评价指标，采用便携式表面粗糙度测试仪进行测量，观测表面粗糙度的变化，并对所得数据进行分析。

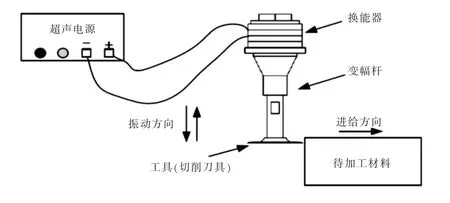
图1 实验装置示意图

1.2 实验方案与结果

实验选用中心复合实验（CCD）确定因素水平，进行实验设计。选用主轴转速（A）、切削速度（B）、进给量（C）和超声波振幅（D）作为研究变量，将评价工件质量的主要参数：表面粗糙度（Ra）确定为响应变量。通过单因素实验，确定加工参数的实验水平分为：-1 水平、0 水平和1 水平，具体水平编码见表2。

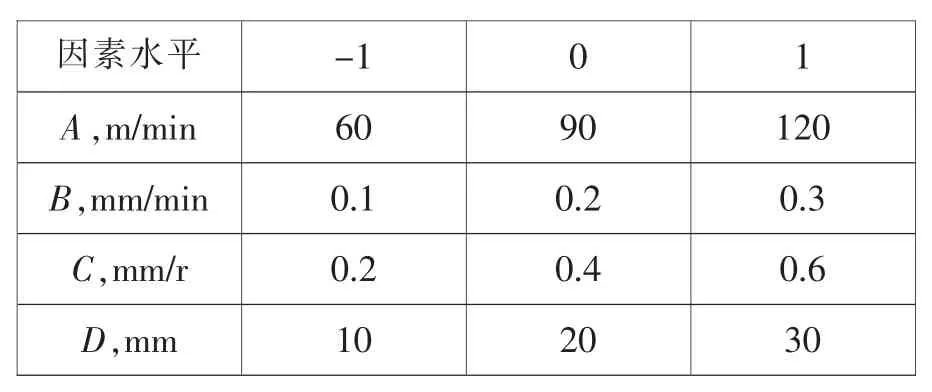
表2 工艺参数因素编码水平表

用CCD 方法设计的实验方案中工艺参数组合进行实验，使用表面粗糙度测试仪对试验结果进行多次测定，取其平均值作为最终实验结果。最终实验方案与实验结果如表3 所示。

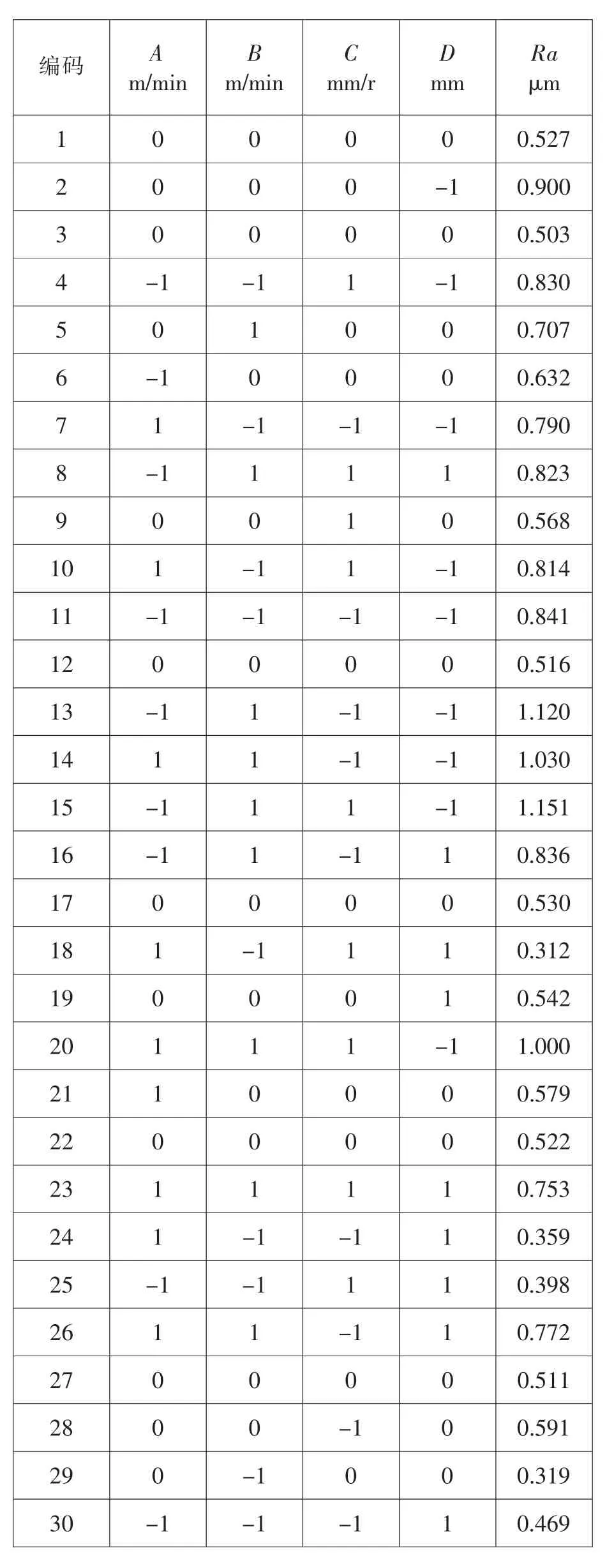
表3 实验方案与实验结果

2 数据处理

2.1 超声振动切削加工数学模型的建立

根据响应面原理[9]：如果在一个实验过程中包括n 个影响因子σ1，σ2，…，σn（均为自然变量），那么输入输出的响应模型为

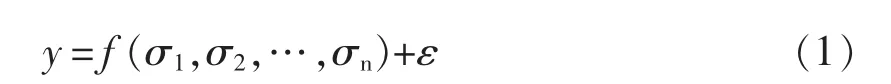
其中：f 为目标响应函数；ε为模型所在系统的误差。

如果目标响应满足

那么式（2）表示的曲面就是响应曲面。为更加方便地研究影响因子，要将自然变量转化为无量纲的规范变量x1，x2，…，xn，则规范后的响应曲面函数即为

由于目标响应与优化参数之间的函数关系是未知的，所以建立响应曲面模型首先要找到逼近真实函数关系的式子。通常情况下，对于响应曲面要用高阶多项式来逼近，例如二阶模型

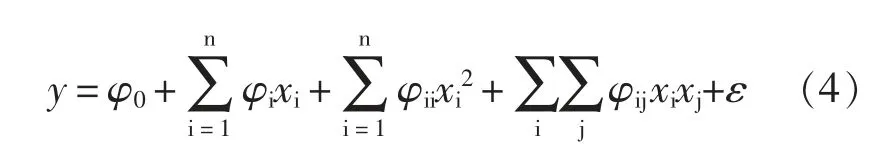
式中φ0，φi，φii，φij均为用最小二乘法估计的多项式系数，ε 为随机误差，则超声振动切削加工的响应曲面模型为四因素二次响应曲面模型，具体为

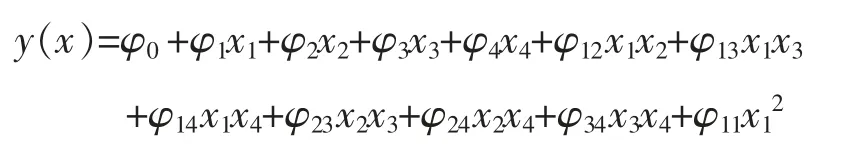
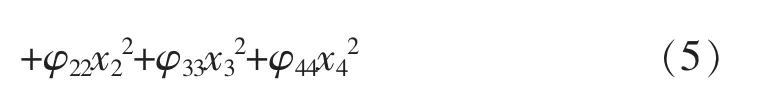
根据表3，利用最小二乘法拟合出具体的二阶模型为

这里R1对应的是表面粗糙度，A、B、C 和D分别对应主轴转速、切削速度、进给量和超声波振幅。

2.2 超声振动切削加工数学模型有效性检验

为验证超声振动切削工艺参数与响应变量模型的预测精度是否准确，选择软件对表3 中的数据进行后期的处理分析。一个模型是否合适，首先要进行有效性检验，残差正态概率图通过分析残差的正态概率分布是否遵循一个直线来判断回归模型的有效性[10]。由图2 可以看出，所有点都有规律地分布在一条直线上，这意味着模型是有效的。

图2 残差正态概率图

2.3 超声振动切削加工数学模型显著性检验

为研究超声振动切削加工中每个工艺参数对粗糙度的影响程度，响应曲面模型还要进行显著性检验。模型的显著性也是判断模型预测精度的重要标准，因此要对实验结果进行方差分析，判断其显著性，分析结果见表4。其中p 值用于分析对象显著性，p＜0.0001 表示响应模型达到了极显著的水平，p＜0.05 表示响应模型达到了较为显著的水平，p＞0.1 表示响应模型不显著[11,12]。

由表4 可知，所建模型的影响是显著的，这说明模型的预测精度较高。此外，由p 值可以判断出，对于线性效应，主轴转速A、切削速度B、超声波振幅D 对表面粗糙度的影响是极为显著的（p＜0.0001），进给量C 对表面粗糙度的影响是不显著的（p＞0.1）。比较均方值的大小可知，影响表面粗糙度的线性效应主次排序为：D＞B＞A＞C；对于二次效应，D2对表面粗糙度的影响是极为显著的（p＜0.0001）；A2对表面粗糙度的影响也是较为显著的（p＜0.05），B2，C2对表面粗糙度的影响是不显著的（p＞0.05）,比较均方值的大小可知，影响表面粗糙度的二次效应主次排序为：D2＞A2＞C2＞B2；对于交互作用，BD 对表面粗糙度的影响是极为显著的（p＜0.0001），其余因素的影响是不太显著的（p＞0.1），比较均方值的大小可知，影响表面粗糙度的交互作用主次顺序:BD＞CD＞AB＞BC＞AD＞AC。表中失拟项（lack of fit）的p 值表现为不显著，证明模型有良好的可靠性。

表4 表面粗糙度的方差分析

将上述模型的后16 组计算结果与实验结果进行对比，如图3 所示，相对预测误差如图4 所示，基本控制在10%以内。实验值与计算值的偏差较小，说明应用模型是可行的。

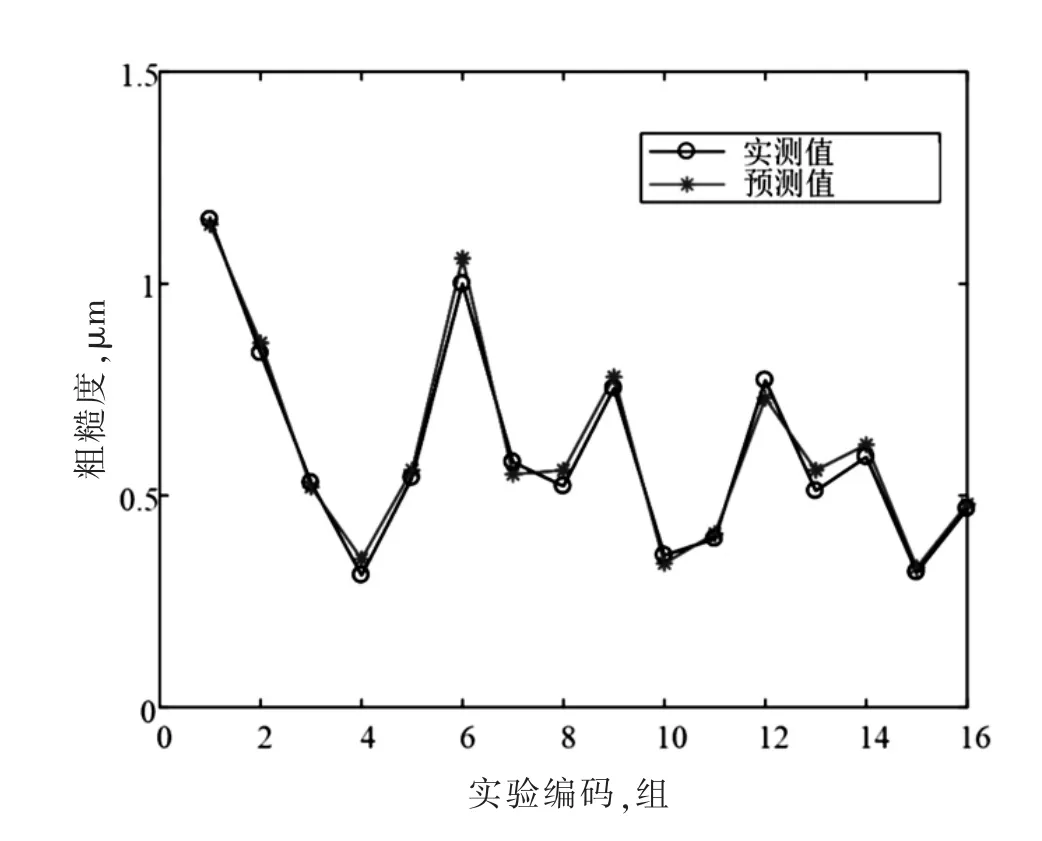
图3 计算结果与实验结果对比

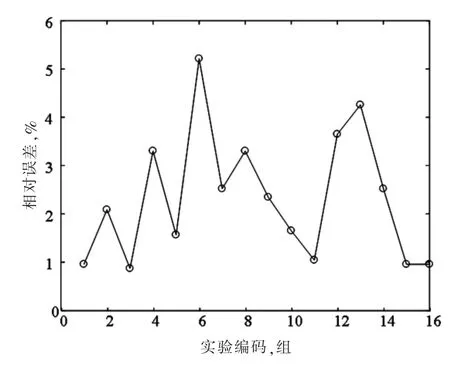
图4 相对误差波动图

2.4 基于RSM 和GA 的参数优化

2.4.1 响应曲面的分析

由于超声振动切削加工工艺产品的表面粗糙度会受到多重因素的影响，各因素之间还存在着交互作用，可以利用响应曲面法对表面粗糙度模型进行拟合，从而分析影响规律。其响应曲面图如图5 所示。

对于优化的响应目标表面粗糙度，由显著性检验分析可得切削速度B 和超声波振幅D 的交互作用是显著的。图5 是切削速度和超声波振幅（BD）的响应曲面图，由图可得：表面粗糙度随着切削速度的减小和超声波振幅的增加而逐渐减小。

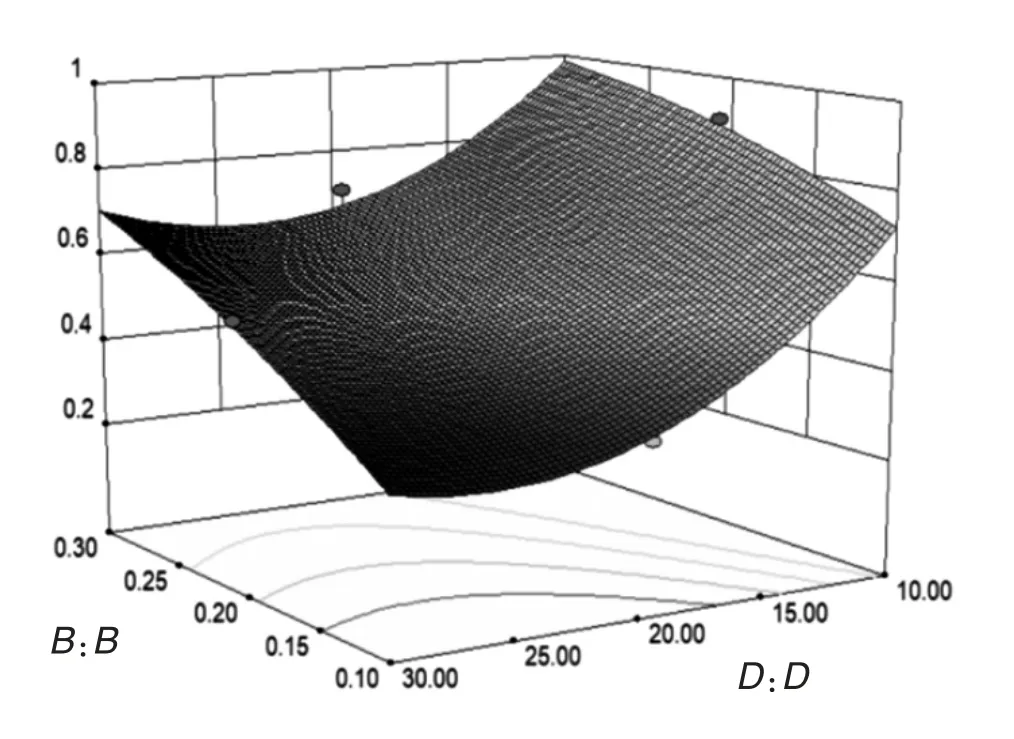
图5 B 和D 影响表面粗糙度的响应曲面图

2.4.2 利用遗传算法进行参数优化

根据加工原理，表面粗糙度越小加工质量越高，以表面粗糙度为响应变量，利用GA 遗传算法进行寻优：

最终得到的最优工艺参数组合为：主轴转速（A）为70.95 m/min、切削速度（B）为0.11 mm/min、进给量（C）为0.95 mm/r 和超声波振幅（D）为26.80 mm，此时的表面粗糙度为0.302 μm。

2.4.3 试验验证

为了验证所提方法的有效性，将经过遗传算法寻优得到的最优工艺参数组合代入仿真模型中，得到的表面粗糙度与试验测试得到的粗糙度进行对比，将表面粗糙度的误差定义为

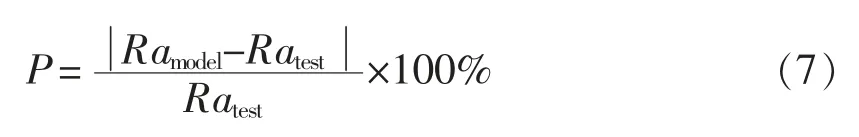
式中 Ramodel——仿真粗糙度

Ratest——试验测试的粗糙度

根据得到的最优工艺参数组合，再次进行实验得到的表面粗糙度为0.315 μm，相对误差为4.3%，误差较小，说明用到的优化方法准确可靠，对超声振动切削加工工艺的优化具有一定的参考价值。

3 结论

（1）采用响应曲面法，建立了预测精度较高的二阶响应模型，进行有效性检验和显著性检验，由残差概率分析、方差分析等得出了表面粗糙度线性效应、二次效应、交互效应的影响顺序。

（2）研究发现切削速度和超声波振幅对表面粗糙度有显著影响，通过响应曲面和方差分析充分描述了这一点，为优化工艺参数提供了依据。

（3）基于遗传算法发现，在超声振动切削加工中，当主轴转速（A）为70.95 m/min、切削速度（B）为0.11 mm/min、进给量（C）为0.95 mm/r 和超声波振幅（D）为26.80 mm 时，表面粗糙度最小，为0.302 μm。再次进行试验验证，发现表面粗糙度为0.315 μm，说明优化模型和方法较为准确。结果表明：合适的超声振动切削加工参数更有利于提高切削质量，为超声振动加工中工艺参数的选择提供了理论基础。