坦克炮控系统RBF神经网络自适应鲁棒控制方法研究
2023-01-03王一珉杨国来王丽群
王一珉, 杨国来, 王丽群
(南京理工大学 机械工程学院,南京 210094)
坦克具有攻防性能兼备,抗干扰能力高,集群战斗力强等诸多优点,现在仍然是世界各国常规武器装备中的首要兵器,在现代战争中起着非常重要的作用。坦克炮口扰动的影响因素十分复杂,包括了耳轴间隙、衬瓦摇架间隙、身管柔性等多因素,呈现典型非线性特征。同时,现代化战争也对坦克的高精度射击提出了更高的要求,现代智能控制算法也被逐渐应用到坦克炮控系统之中[1-6]。由于车炮系统的非线性多因素未能被准确建模,使得控制器设计存在一些固有缺点。随着近年来数值分析技术的发展,非线性有限元理论、多体系统刚柔耦合建模[7-10]等都得到进一步扩充,为复杂车炮系统动力学研究提供了条件。
王烨波等[11-12]通过设计自适应鲁棒控制器,对优化目标进行稳定控制研究,然而未能准确考虑优化目标中的不确定因素对控制性能的影响,仅通过数学表述的方式进行了表达。胡鑫等[13]对带有电动缸建模的坦克炮系统进行了随动系统控制研究,但其建模中也未考虑到实际车炮多体系统的复杂情况。张博等[14]基于RBF(radial basis function)神经网络设计了滑模控制器对永磁同步直线电机进行了位置控制,提出了基于RBF神经网络的非线性观测器。刘恒沙等[15]对影响火炮射击稳定精度的参数进行了研究,通过仿真对全炮28个重要参数进行了灵敏度分析,为兼顾非线性多因素的火炮精细化建模指出了研究方向,但未综合分析非线性多参数耦合对炮口扰动的影响。
对车炮系统的主要非线性因素[16-18]进行多体动力学建模,设计坦克炮控系统自适应鲁棒控制器,对自适应鲁棒控制中的未建模扰动进行补偿,通过Matlab/Simulink与RecurDyn软件中多体模型的联合仿真验证,提高坦克炮稳定精度,具有较高的抗扰动性与鲁棒性,也具有重要的现实意义。
1 发射动力学建模与计算
1.1 车炮系统拓扑结构分析
行进间坦克车炮系统多体动力学的建模主要包括履带、车身、炮塔、起落、后坐共5个组成部分。并且涉及到各总成之间的约束连接、装配定位与路面接触副的建立以及大规模复杂结构接触问题的求解。
主要考虑的总成及连接关系,如图1所示。
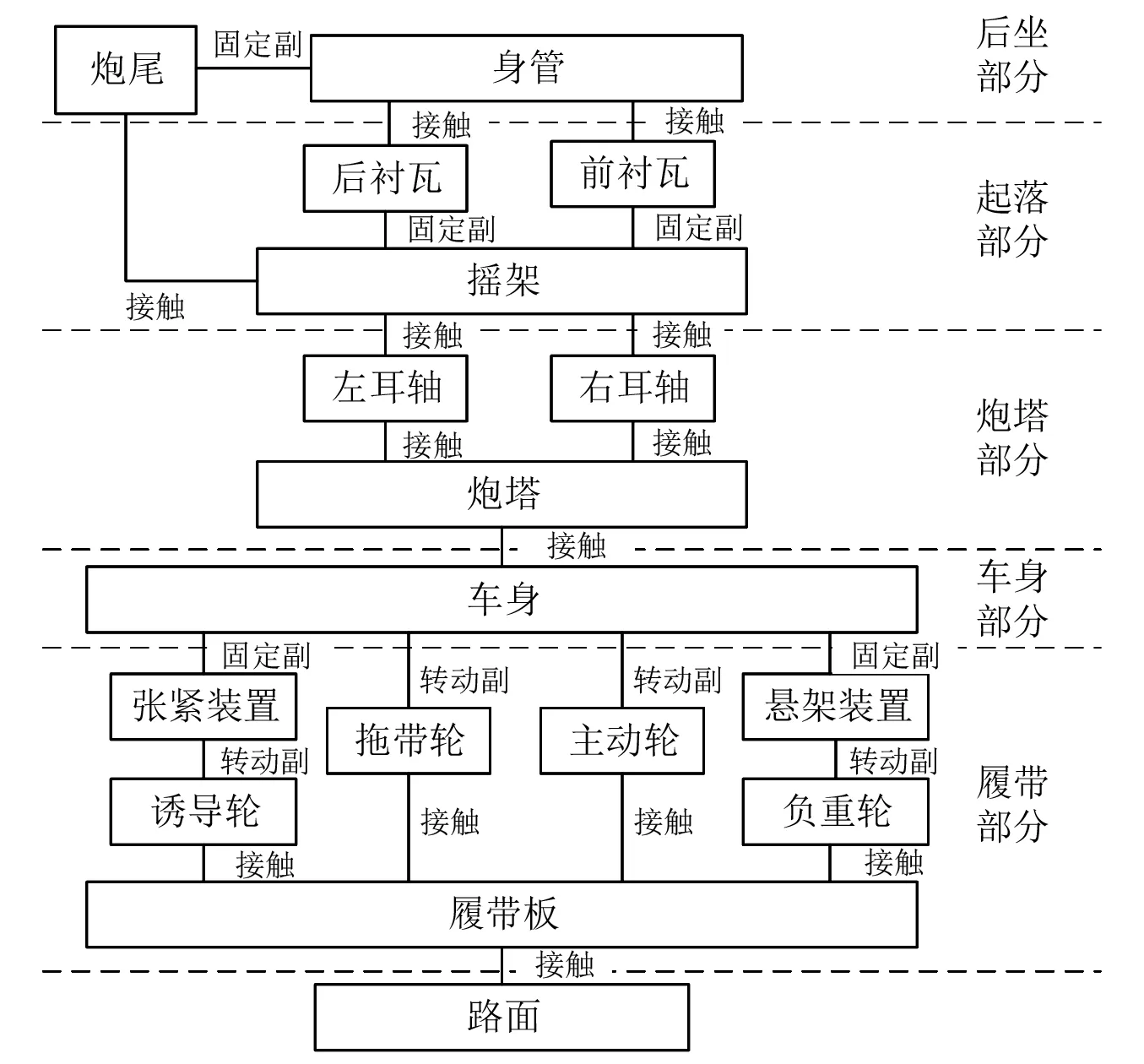
图1 车炮系统主要总成连接方式的拓扑关系Fig.1 Topological diagram of the connection relationship in the vehicle-gun system
1.2 多因素建模基本假设
1.2.1 身管衬瓦接触碰撞建模
在实际的坦克系统中,为了保证后坐过程的顺畅,身管外壁与前后衬瓦之间会存在微小间隙[19]。坦克炮身管分别与前衬瓦、后衬瓦间隙接触关系示意图,如图2所示。
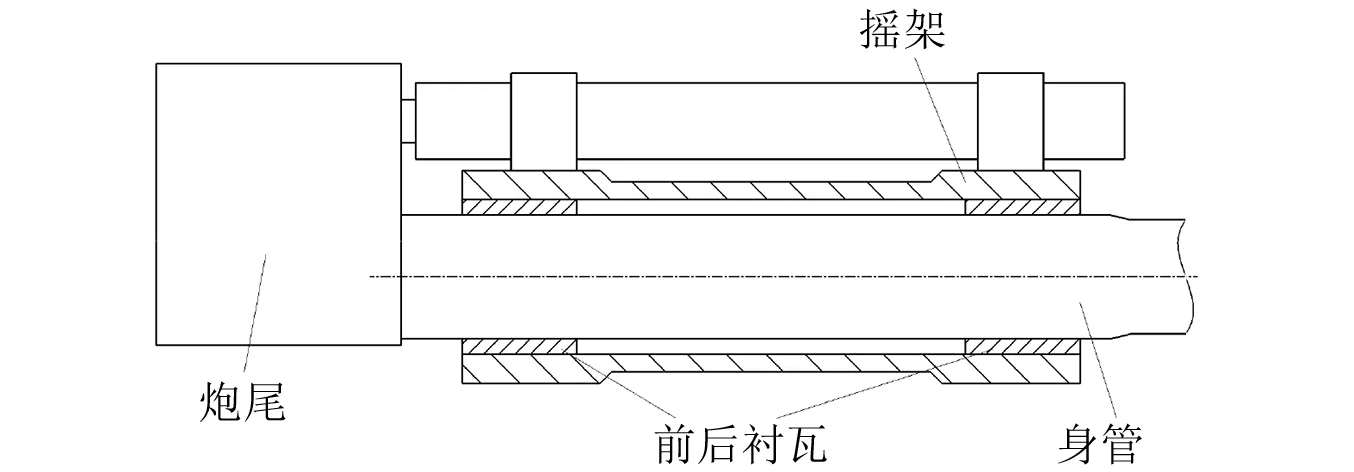
图2 身管-前后衬瓦间隙接触模型示意Fig.2 Gap contact model between barrel and the bushings
采用非线性弹簧-阻尼模型来计算身管与衬瓦间的接触碰撞力。其计算法向接触力F的表达式为
(1)
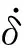
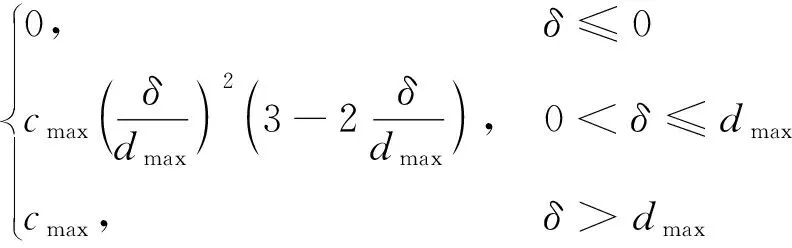
(2)
式中:cmax为最大阻尼系数;dmax为最大穿透深度。
1.2.2 耳轴间隙接触碰撞建模
在已有的车炮系统多体动力学建模中,通常将耳轴与耳轴轴承的关系简化成以耳轴中心为铰点的理想转动副。但在实际运动中,忽略耳轴与耳轴轴承之间的接触碰撞会导致较大的误差。耳轴-耳轴轴承间隙接触模型,如图3所示。
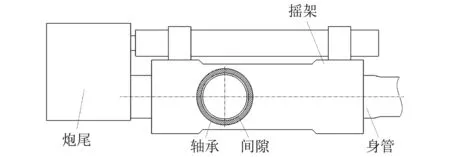
图3 耳轴-耳轴轴承间隙接触模型示意Fig.3 Gap contact model between trunnion and bearing
考虑到耳轴与耳轴轴承之间的间隙较小,并不满足Hertz接触理论中的非协调接触条件。本文根据含有间隙的旋转铰模型,采用含非线性刚度的接触碰撞算法计算耳轴轴承间的接触力,其表达式如下
(3)
式中,K为刚度系数,其表达式为
(4)
式中:E*为复合弹性模量;第二项为碰撞过程中的阻尼力项,对碰撞时的能量损失进行了描述;D为阻尼系数,其表达式为
(5)
式中,ce为碰撞恢复系数。
1.2.3 身管柔性体建模
现代坦克炮可视为长径较大的薄壁空心梁,炮控系统控制精度受其弹性影响较大。坦克炮身管的材料主要是均质炮钢。身管是一种管状结构,内部半径恒定,外部半径逐渐增大。
根据Euker-Bernoulli梁理论,弯矩M(x,t)与挠度y(x,t)的关系可以表示为
(6)
式中:E为炮钢的杨氏模量;Ix为截面转动惯量。变截面身管的横向自由振动微分方程表示为
(7)
式中,ρ为炮钢密度。
设身管的垂直变形为简谐振动,满足y(x,t)=W(x)cosωt,则身管的最大动能为
(8)
不计剪切力做功,身管应变能为
(9)
由于ymax(x,t)=W(x),转角θ非常小时有
(10)
结合式(8)和式(10)计算可得Riley quotient为
(11)
设W(x)满足
W(x)=[φ1(x),φ2(x),…,φN(x)]·
[a1,a2,…,aN]T
(12)
式中:φi(x)为满足边界条件的线性无关函数;ai为待定系数,可由式(13)求得
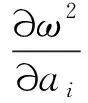
(13)
因此,变截面身管的固有频率ω可以计算出来,并可以计算得到模态函数W(x)。
本研究在有限元软件Hypermesh中采用了8节点六面体单元对坦克身管进行网格划分,如图4所示。身管有限元模型共148 140个网格,184 380个节点。同时,利用RecurDyn中提供的FFlex完全柔性体法[20]对身管进行柔性化建模,并将柔性身管的末端与刚性体炮尾通过界面节点约束进行固定连接,后将身管外壁与前后衬瓦通过用户子程序定义接触约束,如图5所示。

图4 身管有限元模型Fig.4 Finite element model of the barrel
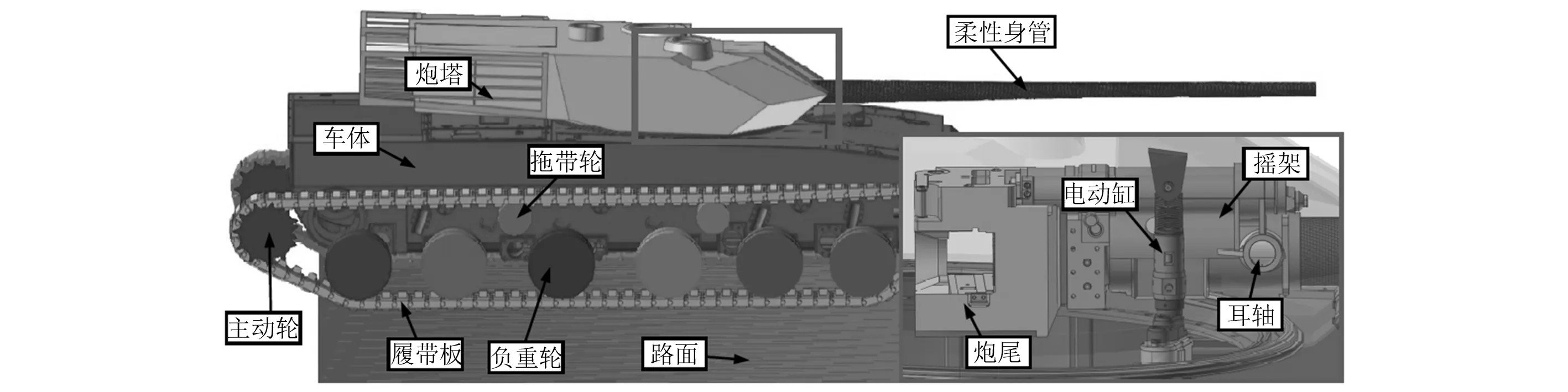
图5 利用RecurDyn软件搭建的车炮系统多体动力学模型Fig.5 Multibody dynamics model of the vehicle-gun system built in RecurDyn
1.3 路面不平度建模
根据路面实际统计特征,路面粗糙度信号为平稳高斯过程。其统计特性通常通过频率域的功率谱密度给出。路面不平度的功率谱密度拟合公式如下
(14)
式中:n为空间频率;n0为参考空间频率;Gq(n0)为路面不平度系数;w为频率指数。
本文基于MATLAB软件中的数学工具利用谐波叠加法编写路面不平度随机生成程序对路面进行重构,分别建立了长为300 m,宽10 m的D级和F级两种路面模型。D级路面三维剖面,如图6所示。
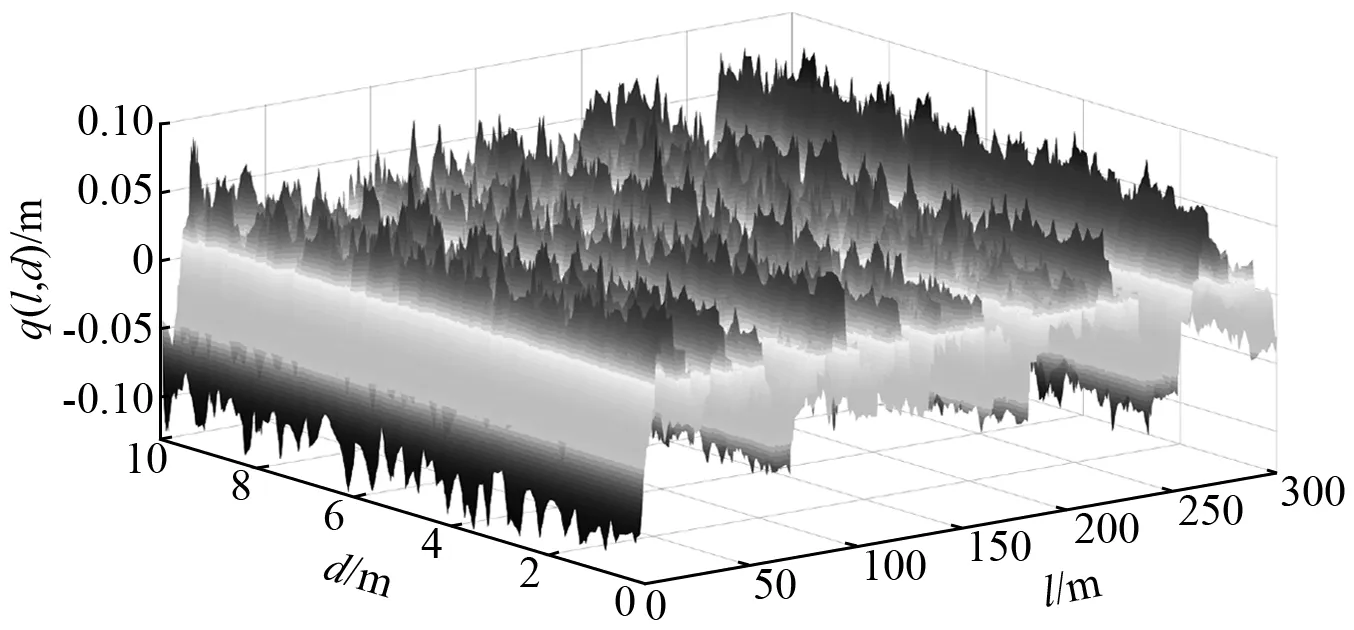
图6 D级路面三维剖面Fig.6 D-level road profile in three-dimensional plot
2 高低向稳定器自适应鲁棒控制建模与分析
2.1 坦克高低向系统数学模型与动力学分析
根据图7所示的坦克高低向系统进行受力分析,可以得到坦克炮身管的高低向运动方程
Jβ=Te-Bω-Tf
(15)
式中:J为坦克炮全部俯仰部分折算在电机输出轴处的转动惯量;β为电动缸电机输出轴的角加速度;Te为电机输出端的转矩,其与驱动器输入的电压指令成近似比例关系,设Kt为电压转矩系数,则有Te=Ktu;Tf为坦克高低向系统折算到电机输出端的负载力矩;B为电机黏滞摩擦因数。
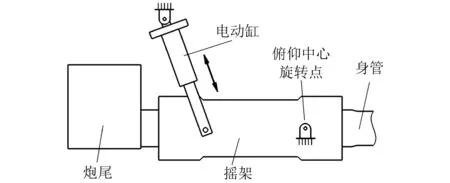
图7 坦克高低向系统主要总成结构模型Fig.7 Main structure model of tank vertical system
Jβ=Ktu-Bω-Tf
(16)
(17)
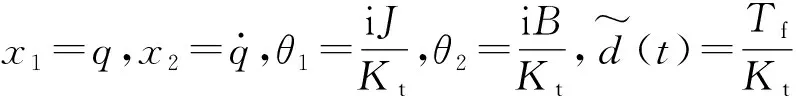
(18)
式中,u0为误差反馈律。定义系统不确定参数θ=[θ1,θ2]T,有如下假设
(19)
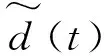
(20)
式中:z1为高低向稳定系统的角度误差;x1d为角度控制指令;k1为反馈增益。
因此,需要控制z2尽可能小,使系统的角误差和速度误差均有更好的表现。
2.2 坦克高低向系统自适应鲁棒控制器设计
按照如下方法设计控制器,使得z2趋近于0。
(21)
由此,设计如下控制器
(22)

(23)
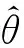
(24)
(25)
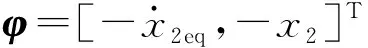
(26)

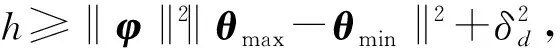
(27)
式中,k2s2为正非线性增益。至此完成了自适应鲁棒控制器的设计。坦克高低向系统控制器的误差反馈律表述为
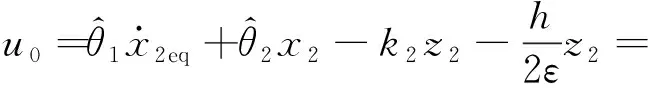
(28)
2.3 基于RBF神经网络的未建模扰动项估计
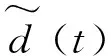
RBF神经网络的隐含层节点使用径向基函数作为激活函数,采用输入节点与中心向量的距离为函数自变量。其结构如图8所示。

图8 RBF神经网络原理框架Fig.8 The principle framework of RBF neural network
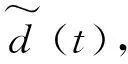
(29)
其输出结果为
(30)
式中:WT为连接隐含层与输出层的权重矩阵;hk(x)为隐含层的非线性函数;ε为逼近误差。非线性函数hk(x)选择如下
(31)
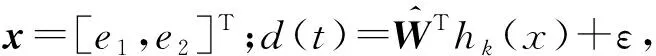
(32)
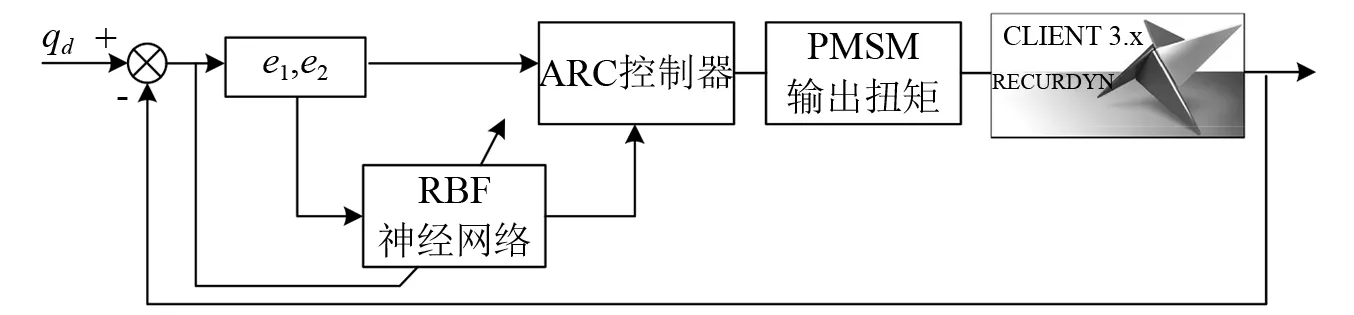
图9 本文炮控系统控制器与车炮系统多体模型联合仿真流程Fig.9 The co-simulation flow chart of gun controller and vehicle-gun system multibody model
3 联合仿真分析
根据图9搭建Matlab/Simulink与RecurDyn多体模型的联合仿真模型,计算坦克在不同行驶工况下控制器的控制效果。研究中联合仿真系统模型的原理图,如图10所示。
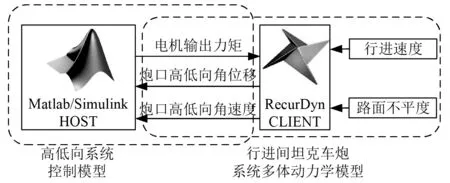
图10 联合仿真系统模型原理Fig.10 Principles of co-simulation system model
通过坦克炮的稳定精度来表征控制器性能[21],其为炮口角振动振幅的算数平均值
(33)
式中:n为总的采样点数;θi为每个采样点的炮口俯仰角度。
为了验证上述算法有效性,本文中对未建模扰动补偿的RBF神经网络坦克炮自适应控制与常规PID(proportional integral derivative)控制进行仿真比对。炮控系统高低向的永磁同步电机主要参数,如表1所示。

表1 永磁同步电机主要参数Tab.1 Parameters of PMSM in this article
3.1 角度跟踪性能分析
仿真时长设计为10 s,根据实际坦克炮高低向稳定系统参数,联合仿真中设计最大角速度指令不超过0.436 rad/s,最大角加速度指令不超过0.698 rad/s2。在4 s时给一个0.1 rad的阶跃响应信号。在D级路面下控制算法与PID控制器的跟踪特性曲线,如图11所示。两者均在4.5 s前后分别达到稳定,控制算法跟踪速度略快于PID,且较为平滑,达到指令后超调和振荡都较小。
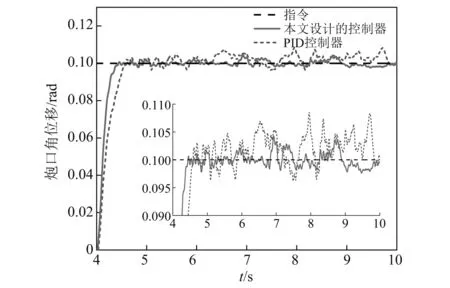
图11 两种控制算法在控制指令为0.1 rad下的阶跃响应Fig.11 The step response of the two controllers under the control command of 0.1 rad
3.2 抗干扰性能分析
坦克分别以20 km/h,30 km/h,在D级和E级两种等级路面条件下,分别基于RBF神经网络补偿未建模动态的自适应鲁棒坦克炮控制器与PID控制器的炮口扰动曲线,如图12所示。10 s内上述4种工况通过式(33)计算出的稳定精度,如表2所示。由表2可知,坦克以20 km/h行驶在D级路面,此时的稳定精度为1.060 mrad,相较于传统PID的2.362 mrad提升了55.12%。
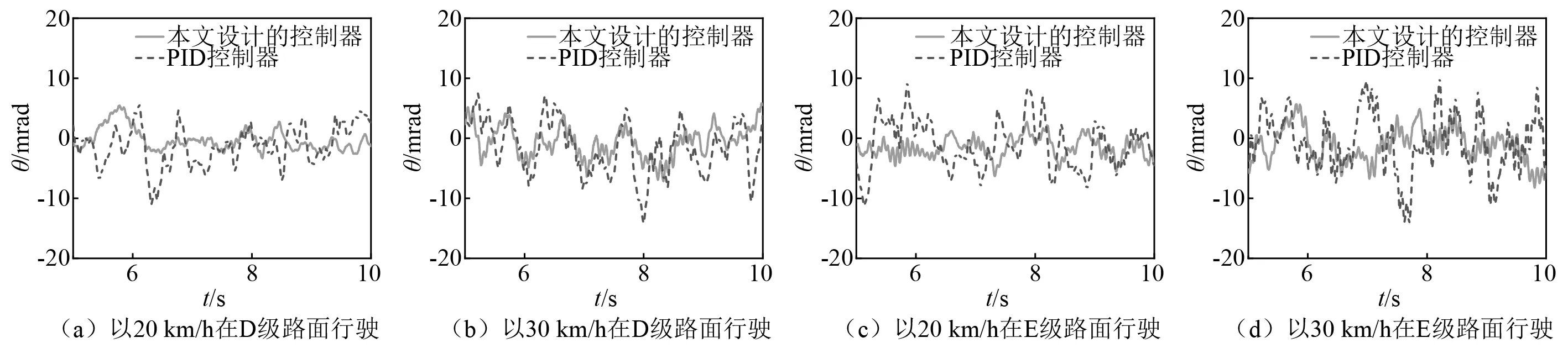
图12 不同车速与路面工况下两种算法的稳定性能比对Fig.12 Comparison of the stability of the two controllers under different vehicle speeds and road conditions
与坦克以20 km/h行驶在D级路面相比,当路面状况变为E级路面,与PID的控制结果相比提升了达到了60.98%;随着车速的提高至30 km/h,与PID的控制结果相比提升了更是达到了62.70%。以上数据表明,随着外界扰动的增加PID算法对坦克的控制效果逐渐变差,而提出的算法体现出较强的鲁棒性与稳定性。
上述仿真结果根据式(33)计算得到的两种控制器分别以20 km/h,30 km/h,在D级和E级两种等级路面条件下行驶得到的稳定精度,如表2所示。
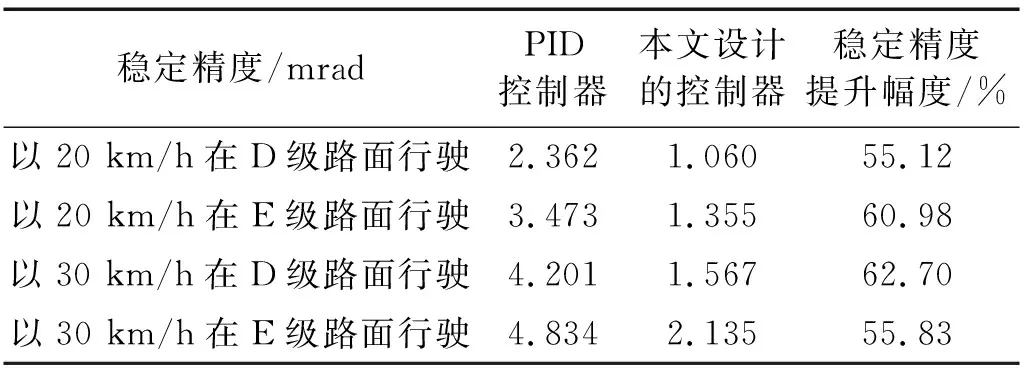
表2 两种控制器在不同工况下的稳定精度Tab.2 Under different conditions in the stability and accuracy of both controllers
4 结 论
标定了包含非线性多因素的车炮系统多体动力学模型参数,并在Matlab/Simulink中针对永磁同步电机伺服控制系统,设计了带有未建模动态补偿的RBF神经网络坦克炮控系统自适应鲁棒控制策略。利用RBF神经网络的自学习能力,对自适应鲁棒控制中的未建模动态误差进行估计补偿。RecurDyn与Matlab/Simulink的联合仿真试验表明,设计的控制器相较于已有PID控制器的鲁棒性与抗干扰能力要好,较未进行补偿的自适应鲁棒控制的跟踪性能优越。
