钢筋混凝土柱-钢梁盒式节点抗剪机理及抗剪承载力计算
2023-01-03刘立平郑歆耀王志军李英民李瑞锋
刘立平, 肖 闲, 郑歆耀, 王志军, 李英民, 李瑞锋, 邓 飞
(1. 重庆大学 土木工程学院,重庆 400045; 2. 重庆大学 工程结构抗震防灾重庆市重点实验室,重庆 400045;3. 重庆保利房地产开发有限公司,重庆 401147)
钢筋混凝土柱-钢梁(reinforced concrete columns and steel beam,RCS)混合结构综合了钢材与混凝土各自的优势,是一种经济高效的结构体系。对比钢结构,钢筋混凝土柱具有更强的耐久性、耐火性和稳定性;而与钢筋混凝土结构相比,钢梁自体质量轻、强度高,提高了空间的利用率,更有利于实现结构的大跨度[1]。对于RCS混合结构,梁柱节点的有效性是保障结构整体性的关键。现阶段,主要的节点形式有梁贯通型和柱贯通型,国内外学者进行了大量的试验研究与理论分析。Parra-Montesinos等[2]对9个3/4比例的梁贯通型外部节点进行了低周反复荷载试验,研究了节点抗弯、抗剪承载力及传力机理,结果表明RCS节点同样适用于抗震设防烈度较高的地区,且刚度无明显削弱。Nishiyama等[3]提出了强柱弱梁作为RCS节点在强地震作用下的设计依据,并建立了12个可应用的柱贯通型梁柱节点模型。传统RCS节点在性能与施工方面存在一定局限性,许多新型节点从而被提出。Alizadeh等[4]结合有限元模型研究了柱端承板与钢梁法兰附加板对于梁贯通型RCS节点位移响应与承载力性能的改良性能。针对梁贯通型节点混凝土浇筑困难的局限性,曹晖等[5]提出新型钢套箍钢筋混凝土梁柱节点,避免梁纵筋贯通节点,降低了施工难度。
同时,马辉等[6-10]对新型RCS混合节点的构造形式、抗震性能和计算方法进行了深入探讨,通过试验得到节点的破坏模式、滞回曲线、位移延性等性能参数并建立了有效的承载力计算公式,对于此类节点的研究具有一定的参考价值。在汲取和消化了国内外学者相关研究的成果和经验后,本课题组提出了一种如图1所示的RCS盒式节点,该类节点由钢梁端板、内部钢腹板、外部钢侧板焊接成为一个整体,对节点区混凝土形成有效约束,钢梁与端板通过焊接连接;腹板开孔增强了与混凝土的黏结和剪力传递,同时方便混凝土浇筑;混凝土柱的纵向钢筋可穿越节点,节点内无需配置箍筋。试验已验证了该类节点的有效性[11],但其传力机理及节点承载力计算方法还有待研究。本文在试验研究成果的基础上,通过理论分析和数值模拟相结合的方法,对该节点受力机理及抗剪计算方法进行了研究,以期对RCS混合结构的推广与应用提供有益参考。
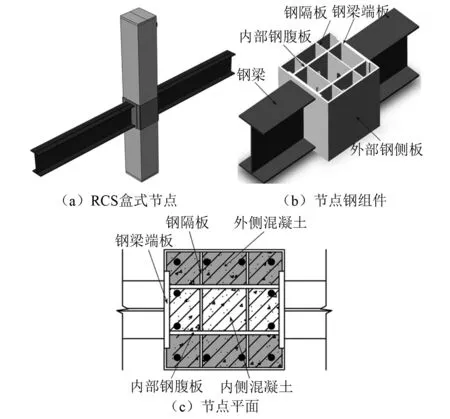
图1 RCS盒式节点构造Fig.1 Construction of RCS box-type joints
在传统RCS混合结构节点受力的理论模型中,节点抗剪承载力主要是由钢梁腹板及混凝土斜压杆提供[12],由盒式节点试验中组件应变分布的特点可类比的认为此类节点抗剪承载力主要由如图2所示两部分提供:其一是由内部钢腹板、外部钢侧板以及钢梁端板共同构成的钢组件;其二是节点区外部钢侧板包裹的内、外侧混凝土组件。为验证以上抗剪机理的有效性,本文基于试验中钢组件的应变分布及变化趋势、数值模拟结果对节点抗剪性能及承载力贡献深入探究,并推导了节点抗剪承载力计算公式。
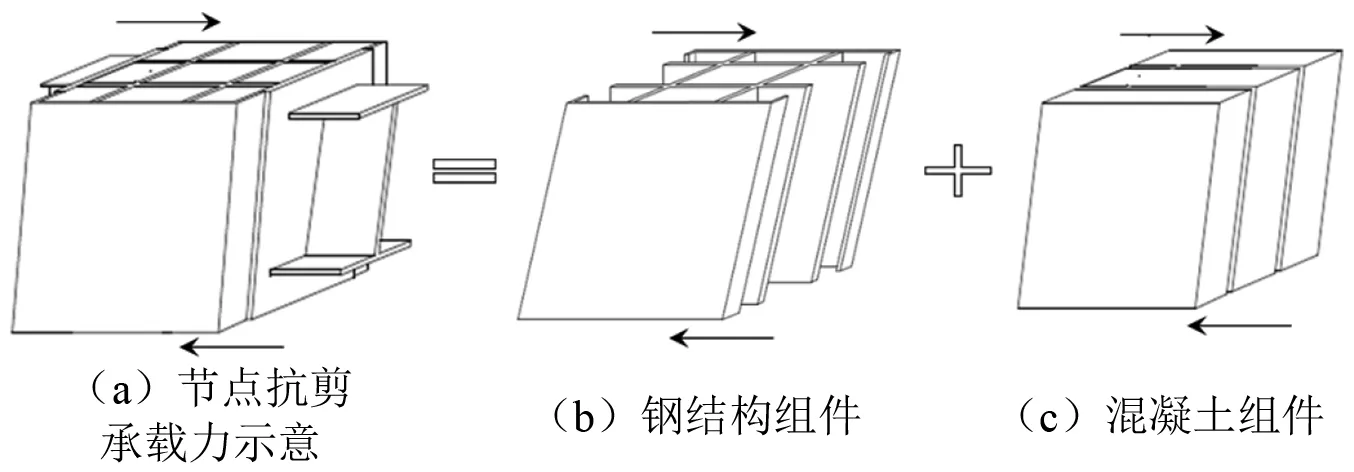
图2 节点抗剪承载力组成Fig.2 Components of shear bearing capacity of joints
1 节点抗剪机理分析
1.1 基于试验结果的抗剪机理分析
试验以RCS 混合框架结构在水平荷载作用下相邻梁柱反弯点之间的典型单元作为研究对象,考虑内部钢腹板厚度、间距以及梁端是否附加盖板加强等主要影响因素制作了4个足尺节点试件RCSJ-1~RCSJ-4,通过对4个试件进行拟静力试验,研究了此类节点的受力特点、破坏特征和滞回性能。试验时位移角幅值分别为1/200(11.6 mm),1/150(15.5 mm)和1/100(23.3 mm)时4个试件各组件测点的最大应变,如表1所示。由表1可知:在位移角幅值为1/200(11.6 mm)时RCSJ-4钢梁翼缘屈服;在1/150(15.5 mm)时RCSJ-2内部钢腹板接近屈服;在1/100(23.3 mm)时所有试件的内部钢腹板都接近或已屈服。4个试件最大应变均出现在钢梁翼缘处,其次为内部钢腹板,可见内部钢腹板是节点承载力的主要贡献者。由循环位移为±15.5 mm 时内部钢腹板的主拉应变和方位角可知,试件RCSJ-1和RCSJ-3的内部钢腹板均体现为斜向轴线上受力,表明内部钢腹板主要受剪力作用。
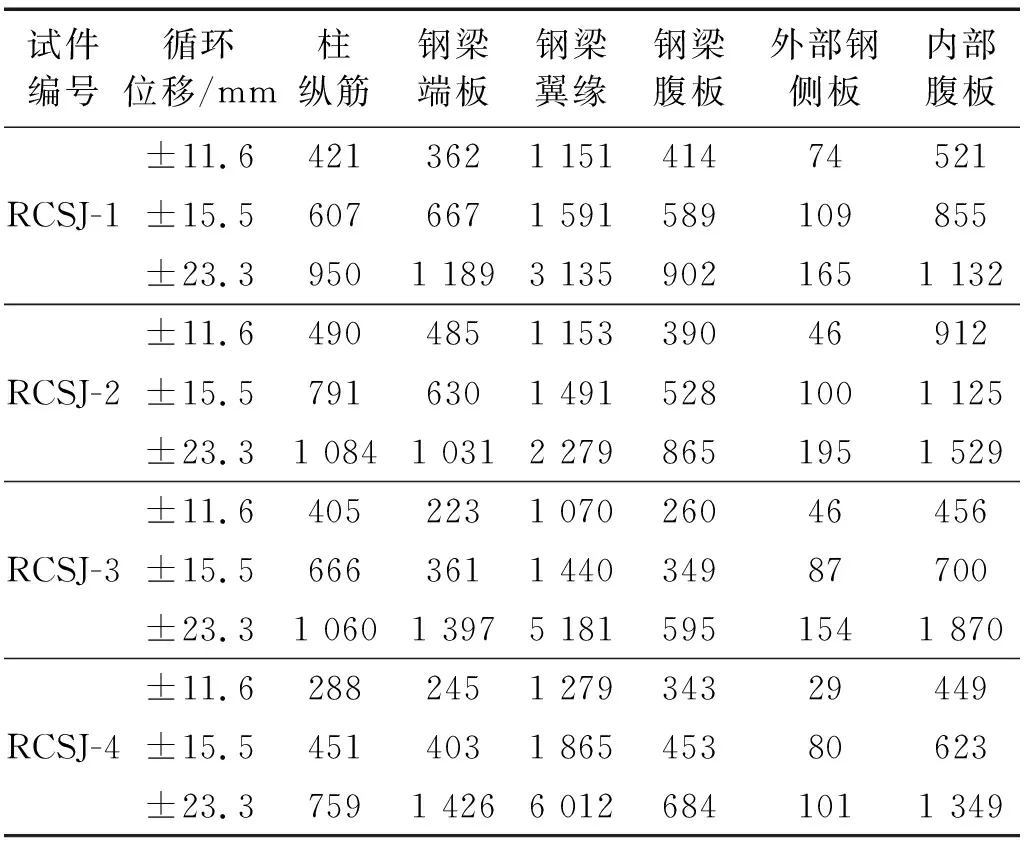
表1 试件钢组件各测点应变最大值Tab.1 Maximum strain values at each measuring point of specimen assembly 单位:με
试件在加载初期处于弹性状态,内部钢腹板和外部钢侧板应变较小,均未达到屈服应变,此时钢组件承担很小一部分剪力,如图3(a)、图3(b)所示。图3中:ε为钢材应变;Δ为位移幅值。随着位移角幅值增大,节点区内部钢腹板应变开始加快增长,承担剪力比重逐渐增大,起到主要抗剪作用。当位移角幅值到达1/50(±46.6 mm)时,内部钢腹板基本处于屈服状态,外部钢侧板应变增长迅速但未达到屈服状态,说明外部钢侧板主要是起约束作用和部分抗剪作用。参考表1与图3(c),外部钢侧板应变为内部腹板的0.05~0.20 左右,说明其所受应力作用相对于内部腹板来说处于较低水平。
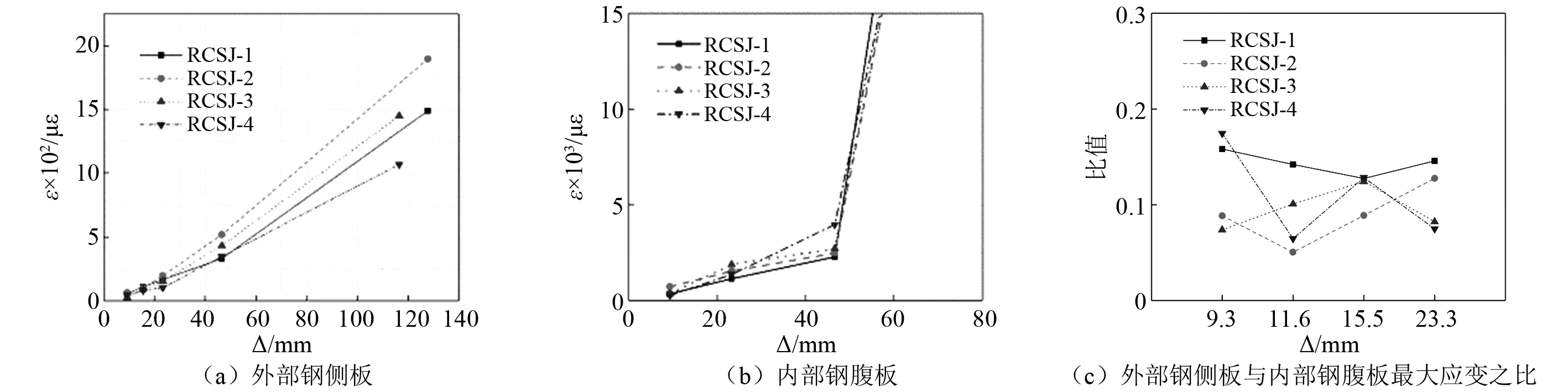
图3 不同位移幅值下试件外部钢侧板和内部钢腹板最大应变及两者应变比Fig.3 The maximum strain and strain ratio of outer steel side plates and inner steel webs under different displacement amplitudes
1.2 基于数值模拟的抗剪机理分析
为进一步研究RCS盒式节点的传力途径和抗剪机理,本节在试验的基础上,通过数值模拟研究各组件的受力机理,为抗剪公式的建立提供依据。
1.2.1 模型及验证
本文选用ABAQUS有限元软件,基于适用低围压下反复加载的塑性损伤混凝土本构模型[13]和GB 50010—2010《混凝土结构设计规范》[14]中建议的混凝土单轴受拉和单轴受压应力-应变关系建立有限元模型,其中流动法则中混凝土的膨胀角对混凝土受力表现的影响较为明显,取30°[15],黏滞系数对结构的刚度影响较大,此处取0.000 5[16]。型钢及钢筋均采用双线性强化模型,本模型考虑了内部钢腹板、钢梁端板以及外部钢侧板与节点区混凝土之间的相互作用,由界面法线方向的接触和切线方向的黏结滑移构成,法线方向的接触采用硬接触,切线方向采用库伦摩擦模型。
下面对产生典型节点区剪切破坏的构件RCSJ-1进行有限元模拟分析,以验证该模型对于此类节点的适用性。参考蒋丽忠等[17-19]对RCS节点的有限元验证方法,将模拟所得的滞回曲线、骨架曲线与试验结果进行对比,如图4所示。图4中,P为荷载幅值。整体而言,ABAQUS软件模拟结果与试验结果吻合良好。验证模型的有效性后,结合数值模拟结果探讨RCS混合节点各部件对于抗剪承载力的贡献,并构建了考虑钢组件及混凝土组件共同工作的RCS混合节点抗剪机理。
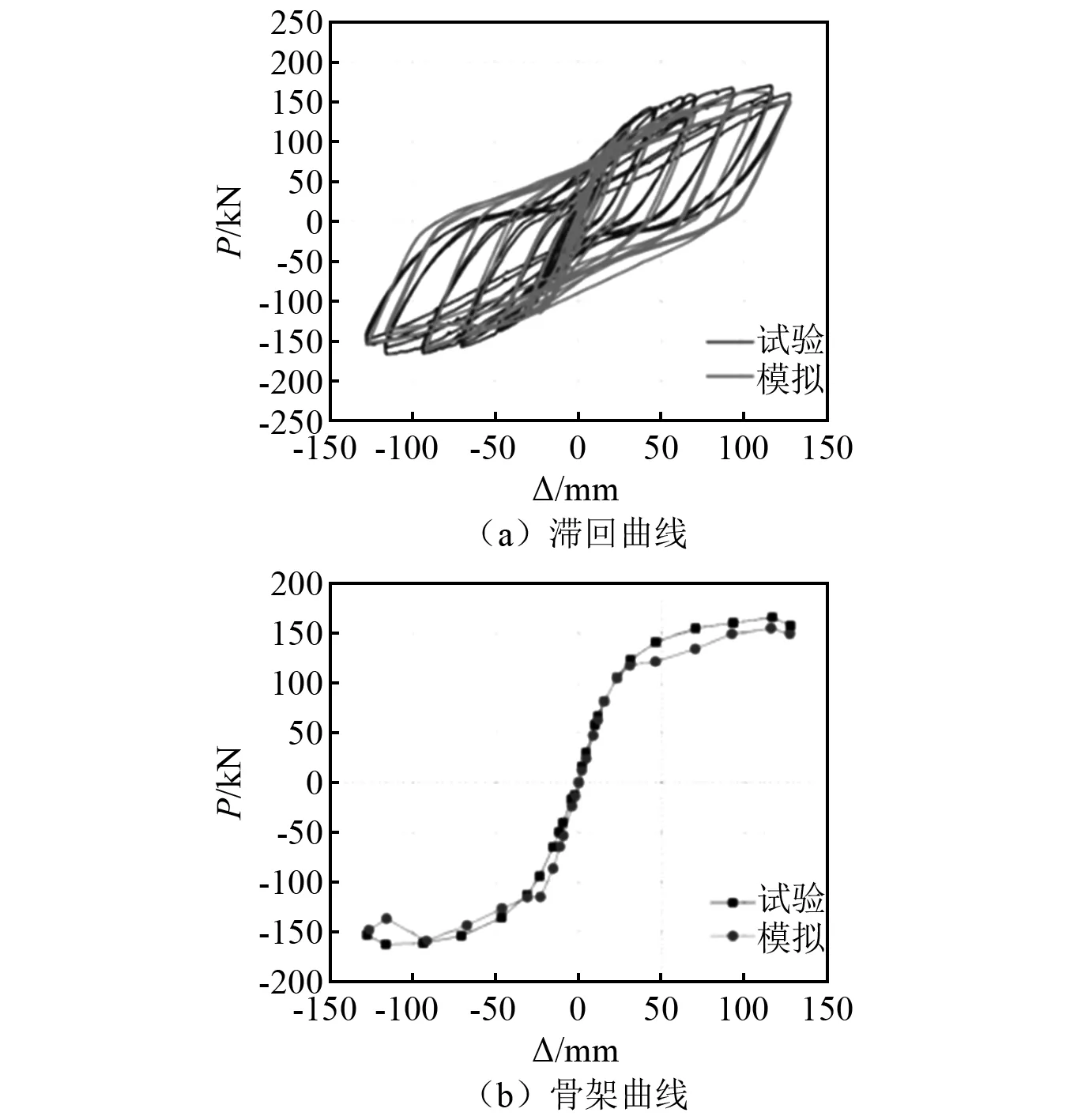
图4 构件RCSJ-1模拟与试验结果对比Fig.4 Comparison between simulation and test results of RCSJ-1
1.2.2 节点区钢组件受力
为研究节点钢组件的受力机理,提取有限元分析中该部分承载力极限状态下的应力分布,如图5所示。由图5可知,钢梁端板与非受力方向的钢隔板的应力水平远小于受力方向的内部钢腹板,从钢梁翼缘传来的剪力主要由内部钢腹板与两侧的外部钢侧板共同承担,钢梁端板及钢隔板对抗剪承载力的贡献可以忽略不计。在柱轴压力作用下,内部钢腹板与外部钢侧板均处于剪应力与压应力共同作用状态。钢梁端板的主要作用是将两端钢梁传来的内力传递到节点区;钢隔板主要作用在于将腹板与两侧外部钢侧板相连,使之形成空间整体;同时与内部钢腹板围合使节点区混凝土处于三向受压状态,从而提高混凝土的抗压强度。
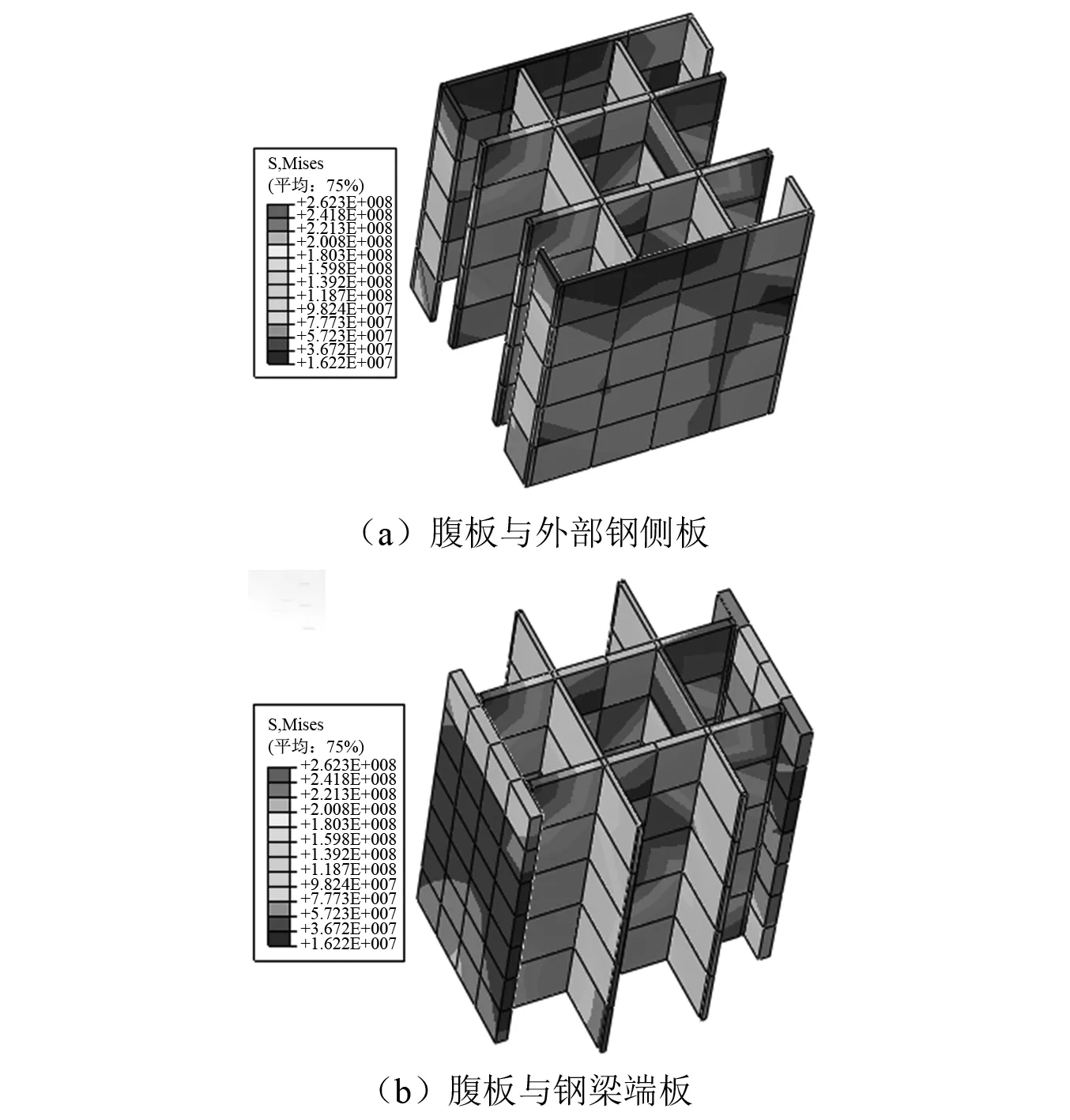
图5 RCS节点区钢组件应力云图Fig.5 The distribution of steel structure part of RCS joints
1.2.3 节点区混凝土组件受力
节点区混凝土屈服点与峰值点的塑性损伤,如图6所示。由图6可知,在屈服点时刻,腹板之间的内侧混凝土塑性损伤明显高于其他部位的塑性损伤。随着位移角幅值的不断增大,节点区腹板剪切变形加大,在钢隔板的带动下,两侧的混凝土也逐渐出现塑性损伤,内部钢腹板间的内侧混凝土塑性损伤最为严重,外侧混凝土次之。因此,除了内侧混凝土起主要的抗剪作用外,外侧混凝土的作用也不可忽略。由数值模拟结果图7可知,外侧混凝土应力分布并不均匀,呈现中间大两边小的趋势,且混凝土的抗压强度未完全发挥,各个模型外侧混凝土中间平均主压应力如表2所示,中间平均主压应力仅有15 MPa左右,而两边压应力仅有5~9 MPa左右。

图6 混凝土塑性损伤分布Fig.6 Plastic damage distribution of concrete
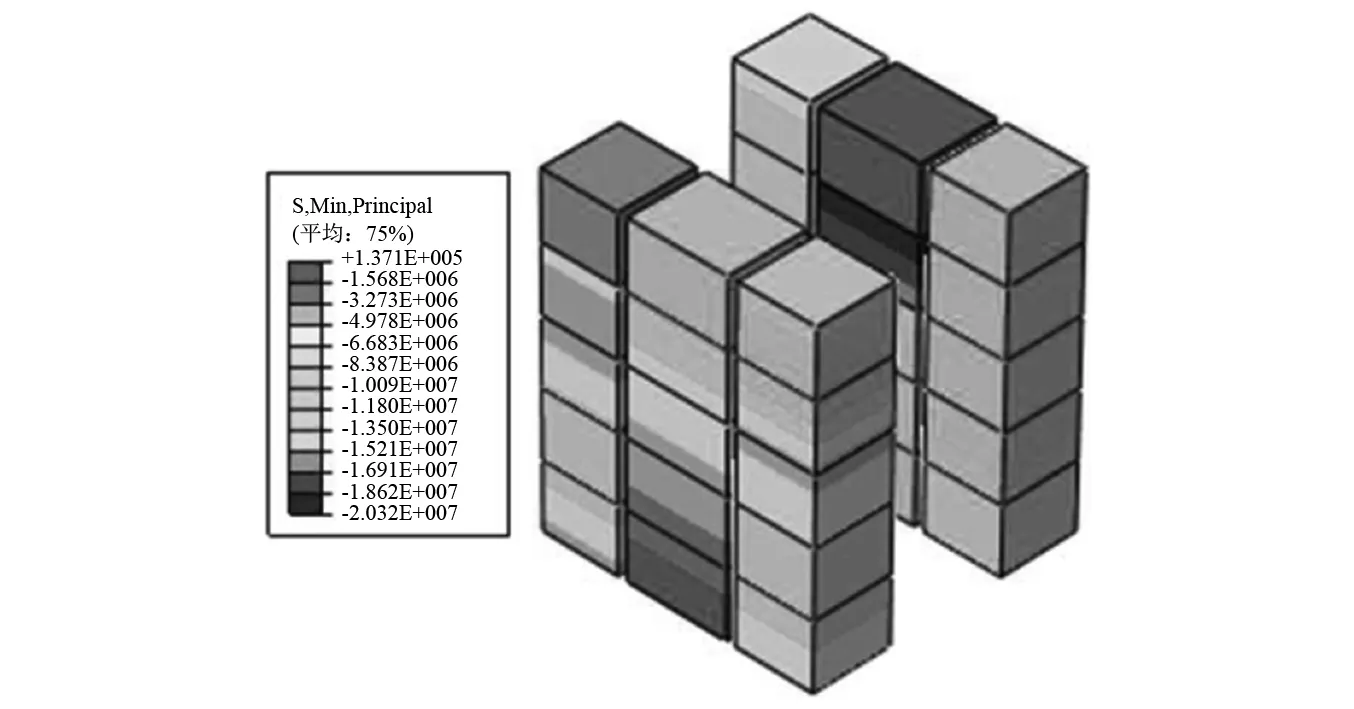
图7 节点区外侧混凝土主压应力分布图Fig.7 Distribution diagram of main compressive stress of concrete outside joint area

表2 各模型外侧混凝土中间平均主压应力Tab.2 Average principal pressure stress of concrete in the middle of each component 单位:MPa
在承载力极限状态时节点区内侧和外侧混凝土主压应力矢量图,如图8所示。由图8可知,节点区内、外侧混凝土处于明显的斜向受压状态,因此本文考虑采用“斜压杆”理论对混凝土组件进行分析。钢梁两端翼缘的压应力通过梁端板的扩散作用,将这部分压应力传至节点区混凝土的角部区域,与此同时,相邻柱端受压区混凝土的竖向压应力,在抵消了部分梁端剪力之后,传导至混凝土的角部区域。两个垂直方向的压应力合成后,沿节点区对角线方向传递,左上角的合力与右下角的合力在斜压杆内相互平衡,从而形成斜压杆机构。
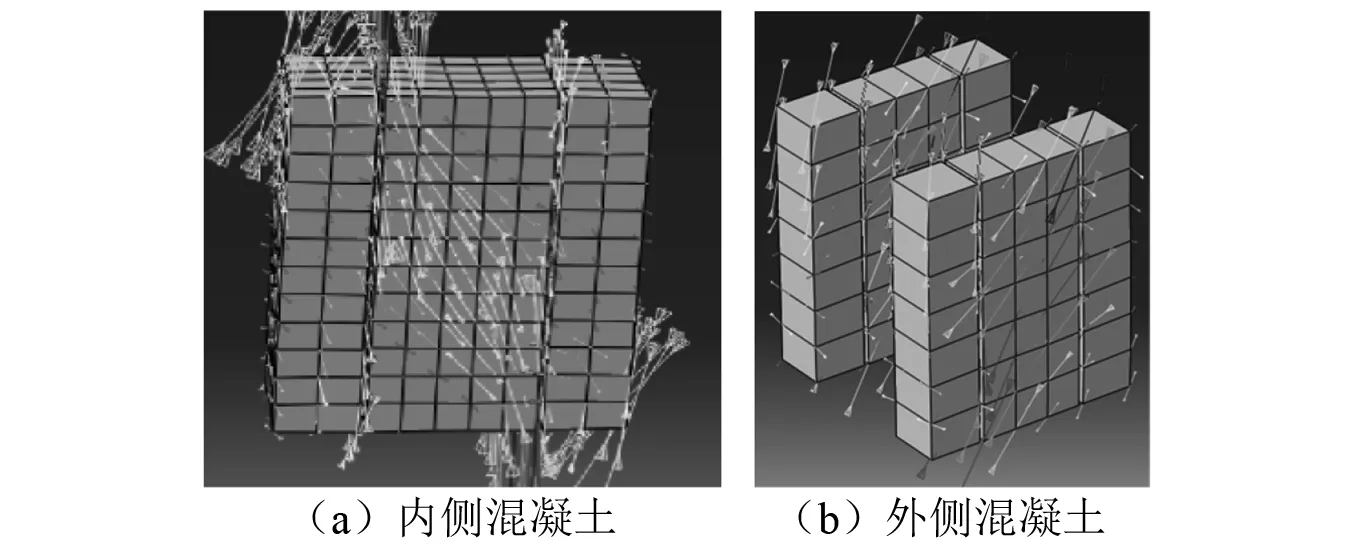
图8 混凝土主压应力矢量图Fig.8 Main pressure stress vectordiagram of concrete
至此,总结以上分析可以认为,RCS混合节点的抗剪承载力主要由节点区钢组件部分和内、外侧混凝土斜压杆机构两部分共同构成,如图9所示。
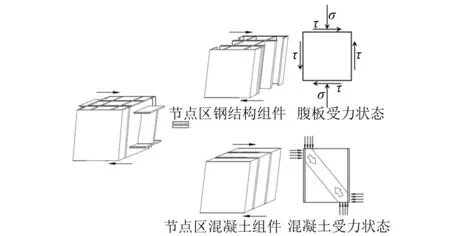
图9 RCS混合节点抗剪机理Fig.9 Mechanism of shear resistance of RCS joints
2 节点抗剪承载力计算
目前RCS混合节点的抗剪承载力公式主要有美国土木工程师协会(American Society of Civil Engineers,ASCE)RCS混合框架节点设计指南建议公式[20]、我国型钢混凝土混合结构技术规程(JGJ 138—2016《组合结构设计规范》)计算公式[21]和日本建筑学会(Architectural Institute of Japan,AIJ)RCS节点设计准则推荐公式[22],其中ASCE公式分别考虑了钢梁腹板项、内侧混凝土斜压杆项、外侧混凝土项以及箍筋项对节点抗剪承载力的贡献,并采用直接叠加的方法将几部分组合起来;我国与日本公式则把节点区混凝土作为一个整体,认为节点剪力由混凝土、钢梁腹板和箍筋三部分承担[23]。由于很难做到将各个受力部分在不同受力阶段所贡献的节点剪力份额进行筛分,故本文参考国内外学者常用手段,基于试验与数值模拟结果,建立半经验半理论的RCS混合节点抗剪承载力计算公式。
2.1 节点区钢组件抗剪承载力
由试验数据及有限元分析可知,当节点达到峰值状态时,内部钢腹板基本进入全面屈服状态,而外部钢侧板此时还处于较低的应力水平,因此,需分开考虑两部分对节点区的抗剪贡献。
2.1.1 内部钢腹板抗剪承载力
对于内部钢腹板,由于轴压力的存在,使其处于压应力和剪应力共同作用的状态,其受力情况如图10(a)所示。其中,σ为柱传来的轴压应力。
内部钢腹板处于弹性状态时,其主拉应力σ1和主压应力σ3如式(1)所示(此时主压应力σ2=0),达到极限状态前适用式(2)所示的Mises屈服条件
(1)
(2)
式中:σy为内部钢腹板抗拉屈服强度;τ为剪应力。将式(1)代入式(2),可得内部钢腹板剪切屈服应力τy为
(3)
由式(3)可知,轴压应力将降低内部钢腹板的抗剪承载能力,因此引入轴压应力不利影响系数φ,参考易勇[24]的研究成果,偏安全考虑取φ=0.8。同时根据Parra-Montesinos等[25]相关研究,在靠近腹板边缘区域存在一定的应力下降,应力分布如图10(b)所示,其中hc为节点水平截面高度。
综合以上因素,可得内部钢腹板所贡献的抗剪承载力表达式(4)
(4)
式中:τweb为内部钢腹板应力;σy采用腹板抗拉强度设计值fy;tw为内部钢腹板厚度。
2.1.2 外部钢侧板
通过1.2.2节对于外部钢侧板的分析可知,外部钢侧板在受力过程中直接承担了一部分节点剪力,但其应力水平较低,对节点区抗剪承载力的贡献难以直接计算。试验过程中RCSJ-1~RCSJ-4试件外部钢侧板中部与内部钢腹板中部在试件开裂、屈服与承载力极限状态下的平均应力比,如图11所示。从构件开裂到构件屈服阶段,外部钢侧板处于较低的应力水平,内部钢腹板起主要抗剪作用,外部钢侧板与内部钢腹板的应力比处于0.25~0.30;构件屈服之后,外部钢侧板逐渐发挥抗剪作用,因此应力比增加到0.33~0.37。可以看出,内部钢腹板与外部钢侧板的应力比处于一个相对稳定的区间,因此参考Deierlein等[26]对混合节点试件中扩展式面承板的研究方法,拟分析不同节点中二者贡献剪力的相对比例,根据规律总结外部钢侧板对于节点抗剪承载力的贡献份额,引入放大系数β来反映外部钢侧板对于节点抗剪承载力的贡献。
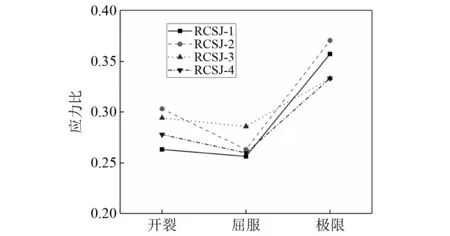
图11 各试件外部钢侧板与内部钢腹板平均应力比Fig.11 Average stress ratio of external steel side plate and internal steel web of each test piece
外部钢侧板厚度分别为2 mm,4 mm和6 mm的有限元模型在极限状态下内部钢腹板中部与外部钢侧板中部的平均应力及其承担的剪力,如表3所示。其中外部钢侧板考虑采用与内部钢腹板相同的受力分析思路。
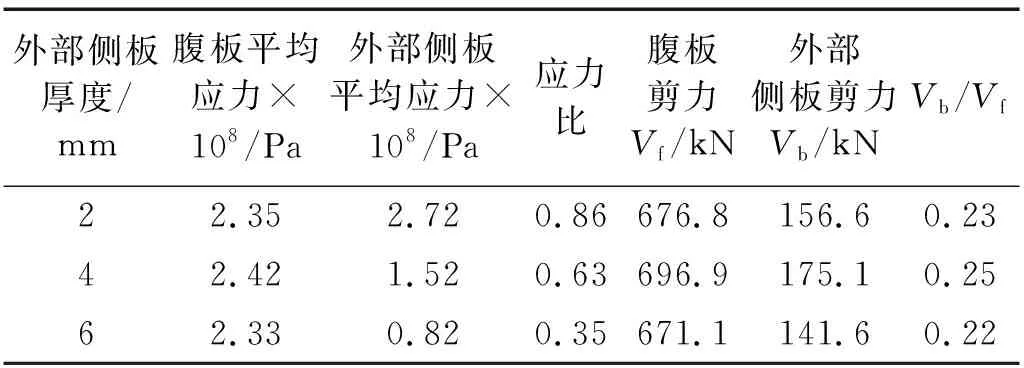
表3 不同外部侧板厚度下外部侧板与腹板平均应力及其承担的剪力Tab.3 Average stress and shear force of external side plate and web under different external side plate thickness
由表3可知,当外部钢侧板厚度不同时,其为节点区贡献的抗剪承载力与腹板为节点区贡献的抗剪承载力之比维持在0.22~0.25,因此,可以认为引入一个考虑外部钢侧板作用的抗剪承载能力放大系数β是合理可行的,偏安全考虑取该比例的下限0.2,故盒式节点放大系数取为β=1.2。
综上所述,内部钢腹板及外部钢侧板对节点区贡献的抗剪承载力表达式可表示为
(5)
式中,fy为抗拉强度设计值。
2.2 节点区混凝土
2.2.1 内侧混凝土
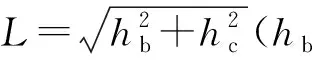
Vc1=fcH(d-tw)cosθ=0.3fchc(d-tw)
(6)
式中:d为内部钢腹板间距;fc为混凝土抗压强度。
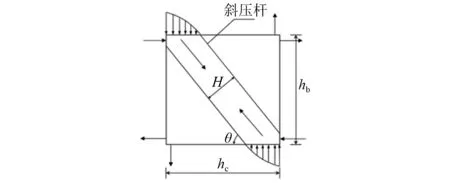
图12 混凝土斜压杆模型示意图Fig.12 Schematic diagram of concrete diagonal strut model
2.2.2 外侧混凝土
外侧混凝土也采用与内侧混凝土相同的分析方法,将其考虑成两个斜压杆。由机理分析可知外侧混凝土应力呈现中间大两边小的分布特点,且混凝土的抗压强度未完全发挥,将外侧混凝土的应力分布近似考虑为图13所示的分布规律,其中则由外侧混凝土贡献的节点区剪力为
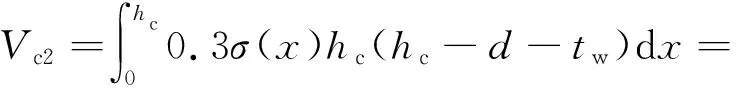
(7)
式中,σ(x)为混凝土压应力。
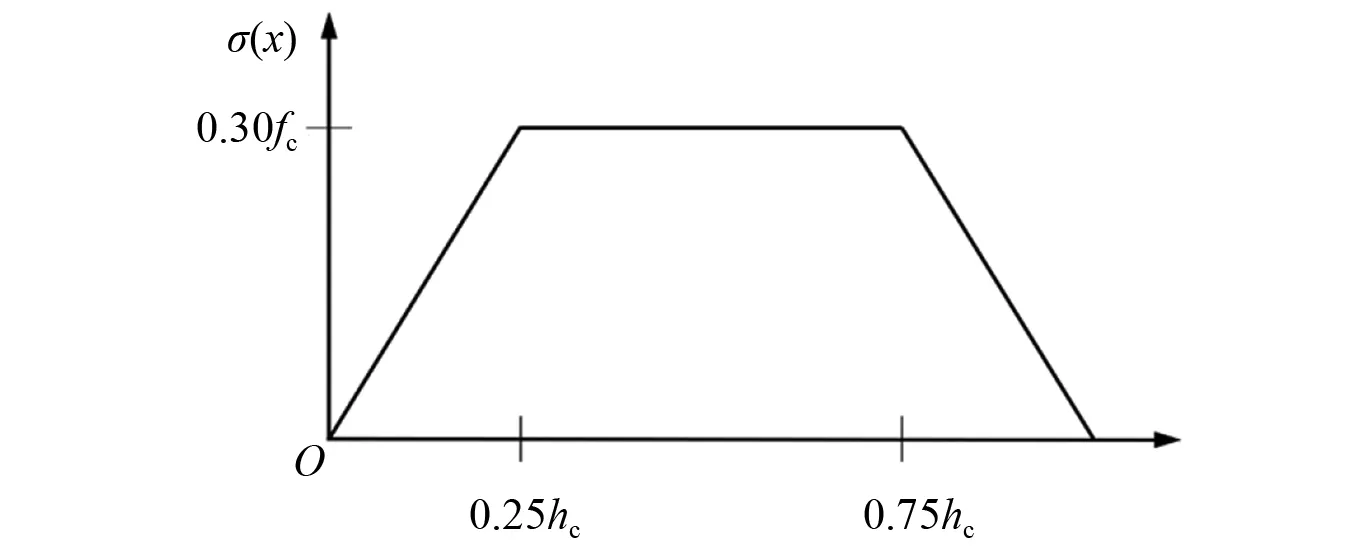
图13 外侧混凝土压应力近似分布Fig.13 Approximate distribution of compressive stress in outer concrete
将处于承载力极限状态的内部钢腹板、内侧混凝土与尚未屈服的外侧混凝土进行叠加即可得到RCS盒式节点的抗剪承载力计算公式
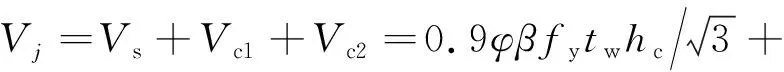
(8)
式中,Vs为内部钢腹板贡献的抗剪承载力。
3 公式验证
分别应用第2章提到的常用公式以及本文推导式(8)进行试件RCSJ-1~RCSJ-4抗剪承载力计算,试件抗剪承载力试验值Vt与计算值Vj对比如表4、表5所示,其中材料强度采用实测均值。从表4、表5可知,美国ASCE、日本AIJ和我国JGJ 138—2016《组合结构设计规范》给出公式的计算值与试验值相比均偏大,主要原因在于美国ASCE计算公式认为整个内部钢腹板为纯剪状态而未考虑轴压力对抗剪承载力的削弱;我国JGJ 138—2016《组合结构设计规范》与日本AIJ公式未区分节点区内侧混凝土与外侧混凝土而高估了节点区混凝土的抗剪承载力。本文推导公式的计算结果与试件的实际抗剪承载力对比,见表5。表5中:RCSJ-1与RCSJ-2由于节点区发生破坏,因此所得试验值与计算值非常接近,仅有5%左右的误差;而RCSJ-3与RCSJ-4由于节点区未发生破坏,所得节点的抗剪承载力试验值失真,故试验值小于理论计算值。又由表5可知,内部钢腹板与内侧混凝土对整个节点抗剪承载力贡献最大,约占总承载力的80%左右。综上可认为,采用现阶段常用的RCS混合节点抗剪承载力公式计算RCS盒式节点偏于不安全;而采用本文推导公式的计算值与试验值吻合良好,且具有较高的精度。
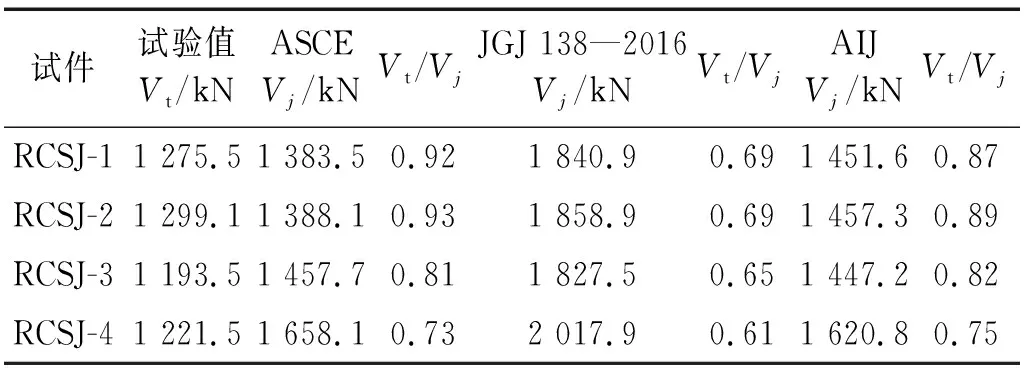
表4 现行RCS节点抗剪承载力公式计算结果Tab.4 Calculation results of current shear capacity formula for RCS joints
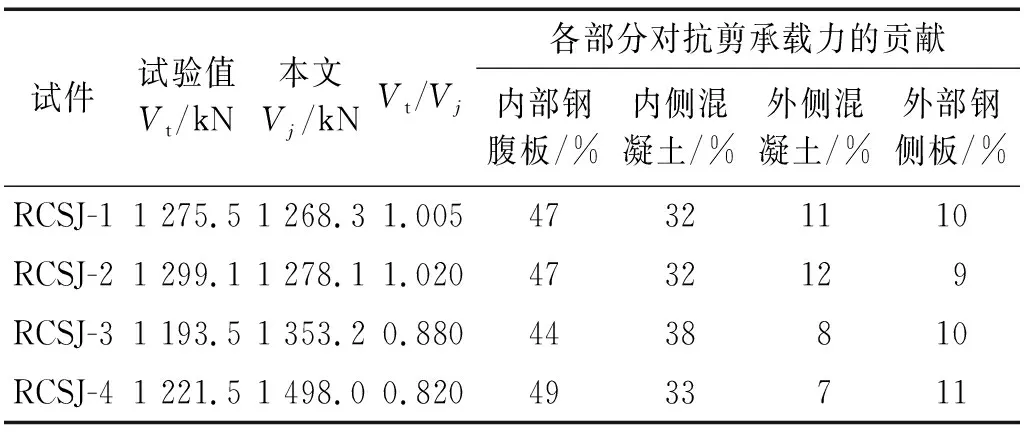
表5 本文RCS节点抗剪承载力公式计算结果Tab.5 Calculation results of shear capacity formula for RCS joints in this paper
为进一步验证RCS盒式节点抗剪公式的有效性,不同参数条件下有限元模型的抗剪承载力模拟值Vs与公式计算值Vj对比,如表6所示。且当外部侧板厚度为0时(取消外部钢侧板),计算公式中不考虑侧板放大系数,即β=1,其中材料强度采用设计值。由表6可知,针对不同的参数条件,有限元模型得到的节点区最大抗剪承载力与按公式计算所得的计算值非常接近,误差均在4%以内,可认为所提计算公式能较为准确地预测该类RCS盒式节点的抗剪承载力。
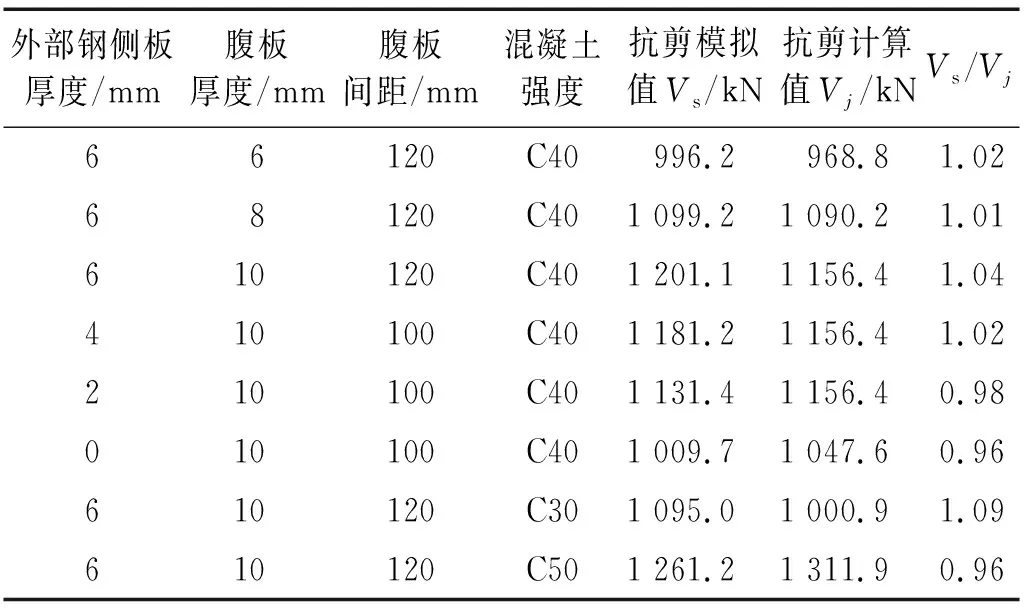
表6 抗剪承载力计算值与有限元模拟值比较Tab.6 Comparison of shear strength between calculation and finite element method
4 结 论
本文基于RCS盒式节点的低周反复荷载试验结果,利用有限元软件ABAQUS分析了节点的抗剪机理,建立了该类节点的抗剪承载力计算公式,主要得到以下结论:
(1) 节点剪力由内部钢腹板、外部钢侧板及内、外侧混凝土共同承担,其中内部钢腹板和内侧混凝土为主要受力部分,其对节点抗剪承载力的贡献分别占比为50%,30%左右;内部钢腹板和外部钢侧板表现为剪压破坏,内、外侧混凝土为斜压破坏。
(2) 在提出的抗剪机理的基础上,建立了分别考虑内部钢腹板、外部钢侧板与内外侧混凝土抗剪机构贡献的RCS混合节点抗剪承载力计算公式,对比发现计算值与试验值吻合良好。同时,利用有限元软件,通过改变不同的节点区构造参数得到的节点区抗剪承载力与按本文建议公式的计算值有较高的吻合度,说明该公式具有一定的适用性和有效性。
