随机激励下非线性能量阱系统减振性能优化研究

胡宏祥， 陈林聪,2

(1. 华侨大学 土木工程学院，福建 厦门 361021；2. 华侨大学 福建省智慧基础设施与监测重点实验室，福建 厦门 361021)

迄今为止，结构振动控制主要分为主动控制、半主动控制、被动控制、混合控制4种技术[1-2]。由其派生出的减振装置各有特点，其中被动控制装置以其设计制造简单、成本低、无需外部供能等优势成为减振首选方案。根据组成元件的特性差异，被动消能减振装置又可分为线性和非线性两种类别。线性装置拥有众多优势，但其主要缺陷也不可忽略。一旦结构的特定模态频率偏离线性装置的固有频率，或者环境激励在其频率带宽之外，就会失去效果甚至会引起系统振动恶化。针对线性装置的缺陷，非线性能量阱(nonlinear energy sinks，NESs)作为一类典型的具有非线性刚度的被动控制装置，因其质量轻、频率鲁棒性强、能量耗散快等优点赢得了工程领域的关注。

当前，国内外关于NES的研究均有较多的成果，但主要集中于确定性载荷作用下的系统响应研究[3-12]，而实际结构往往承受着随机激励。针对耦合NES的随机结构系统的研究尚处于起步阶段。Starosvetsky等[13]采用蒙特卡洛直接模拟的办法验证了单自由度(single-degree-of-freedom，SDOF)系统与NES在窄带随机激励下的减振效果。Xue等[14]利用随机平均法与路径积分法获得了谐波和高斯白噪声组合激励下耦合NES单自由度系统的稳态响应。然而，直接采用随机平均法，完全剔除了NES的影响。随后，薛继仁等[15]又直接采用数值方法求解FPK(Fokker Planck Kolmogorov)方程，获得了高斯白噪声激励下耦合NES的单自由度系统稳态响应，讨论了不同参数下系统的稳态响应特性。文献[16]研究了窄带随机力作用下NES的振动抑制。引入变量将原系统转化为等价系统，采用随机平均法降低等效系统的维数，但采用Hermite级数法求解FPK方程可能会得到负的概率密度函数(probability density function，PDF)。

另一方面，学术界对NES的相关参数，包括质量比、初始条件和阻尼，特别是非线性刚度进行了很多优化研究以期获得更好的减振性能。如，Shiroky等[17]提出了一种系统稳定性评估准则，用于估计NES的最佳阻尼值。Yang等[18]评估了NES参数对非线性系统传输速率的影响。刘良坤等[19]基于强调制反应的特性，得到NES刚度的最佳上下限。Vaurigaud等[20]通过对靶能量传递期间分岔现象的研究，提出了一种NES装置的解析调谐方法，得到了简谐激励下NES的最优刚度。张也弛等[21]在忽略阻尼的保守系统的基础上，利用近似慢变力学模型给出了完全能量传递的临界质量比。可以看出，现有的工作都是属于确定性激励情形，但这些工作可为随机激励下耦合NES结构系统的参数优化问题提供重要的借鉴。

本文针对高斯白噪声激励下耦合NES单自由度结构随机振动的参数优化问题，提出一种高效的数值方法。引入新变量，由原系统得到关于质心位移和相对位移的等价系统；应用加权残值法，将等价系统等效为具有精确平稳解的随机系统，再结合雅可比变换，导出原系统平稳响应概率密度函数的近似解析表达式；最后，以原系统平稳响应概率密度函数的近似解析解构造目标函数，以主结构位移与速度响应量的均方(mean-square，MS)最小为优化准则，确定不同控制条件下的NES最优参数以及变化规律，进而为实物设计提供可行性参考。

1 系统动力学模型

本文所考虑的力学模型由线性主结构和附在其上的NES装置两部分组成。主结构质量m1通过线性阻尼c1和线性刚度k1与地面相连。NES装置由小质量块m2, 三次非线性刚度k2和线性阻尼c2组成。该模型如图1所示。

通过考虑动态平衡条件以及主体结构与NES之间的耦合作用，该系统的运动微分方程为

(1)

式中：X1和X2分别为主体结构和NES'相对于地面的位移响应；F(t)为作用于系统主结构的外部激励。

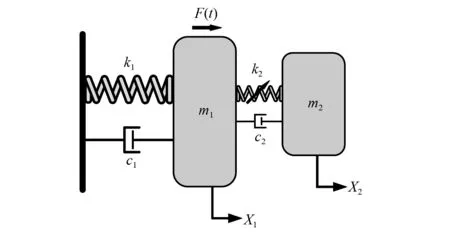
图1 耦合NES的单自由度系统装置Fig.1 A SDOF system coupled with NES device

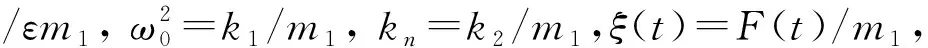
(2)

式中，ξ(t)为强度为2D的零均值高斯过程，满足E[ξ(t)ξ(t+τ)]=2Dδ(τ),E(·)为数学期望，δ(τ)为Dirac delta函数。

现引入新变量

u1=X1+εX2,u2=X1-X2

(3)

式中，u1,u2分别为质心位移和相对位移。结合方程式(2),可得到关于u1与u2的等价系统。结果为

(4)

式中，Ci(i=1,2,…,6)具体表达式如下

(5)

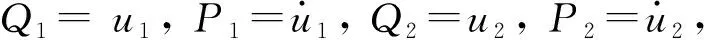
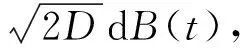
(6)

式中，B(t)为单位维纳过程。

支配系统式(6)的稳态概率密度函数ρ的平稳FPK方程为

(7)

式中，mi(i=1,2,…,4)分别为

m1=p1,m2=-C1p1-C2q1-C3p2-C4q2,

(8)

方程式(7)的精确平稳解一般情况下无法获得。另外，方程维数较高，直接数值求解所需的计算量和数据存储量都较大，诸如有限差分法等数值方法不适合NES的参数优化分析研究。本文提出了一种基于原系统FPK方程与等效系统FPK方程的加权残差最小化技术，求得原始系统平稳解的近似解析表达式，以达到NES参数优化分析的目的。

2 等效随机系统

假设系统式(4)的等效系统如下

(9)

式中：Ci,eq(i=1,2,4,5,6)为待定系数；ξ1(t)和ξ2(t)为两个强度均为D，零均值的独立高斯白噪声。

与式(9)对应的平稳FPK方程为

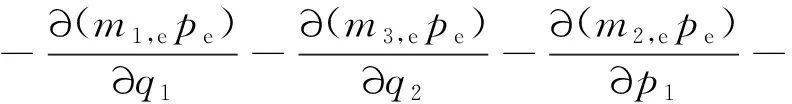
(10)

式中：ρe为等效系统的平稳概率密度函数；mi,e(i=1,2,…,4)分别为

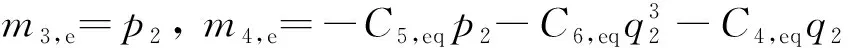
(11)

平稳FPK方程式(10)具有精确平稳解，其表达式为

(12)

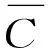
利用ρe取代式(7)中的ρ，得到误差δ

(13)

比较式(13)与式(10)，可进一步得如下表达式

(14)

其中

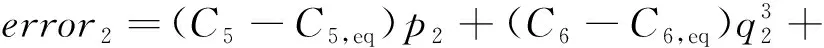
(15)

将加权多项式函数应用于式(14)，并将残差均方在整个域上进行积分，即

(16)

式中，ρf为忽略高阶累积量的截断方法得到的原系统的联合平稳概率密度函数。式(16)中的加权函数建议取如下的多项式形式[22]

总之，小学语文教学中培养学生综合阅读能力是新课标的主要要求。在实际语文教学中，需要教师引导学生进行词句基础训练、教导学生正确阅读的方法及引导学生深入感悟文章的内涵，以让学生掌握文章整体脉络，从而提高学生的综合阅读能力。

(17)

式中，Kij通常取1。

等效系统中的未知系数由最小均方误差准则确定，即

∂E(Δ)/∂Cj,eq=0,j=1,…,5

(18)

式中，E(·)为数学期望。

求解方程组式(18)，即可得到未知系数Ci,eq。将结果代入式(12)，得到等效系统的平稳解。在系统参数ε=0.05,λ1=0.1,λ2=0.1,kn=0.5,ω0=1.0,D=0.01(0.005)时不同激励强度下等价系统式(4)的边缘概率密度响应，如图2所示。图2中：实线为蒙特卡洛模拟(Monte Carlo solution，MCS)的结果；符号为本文方法得到的数值结果，可知理论解和蒙特卡洛模拟解在误差允许范围内吻合，表明文中提出的数值方法有效。

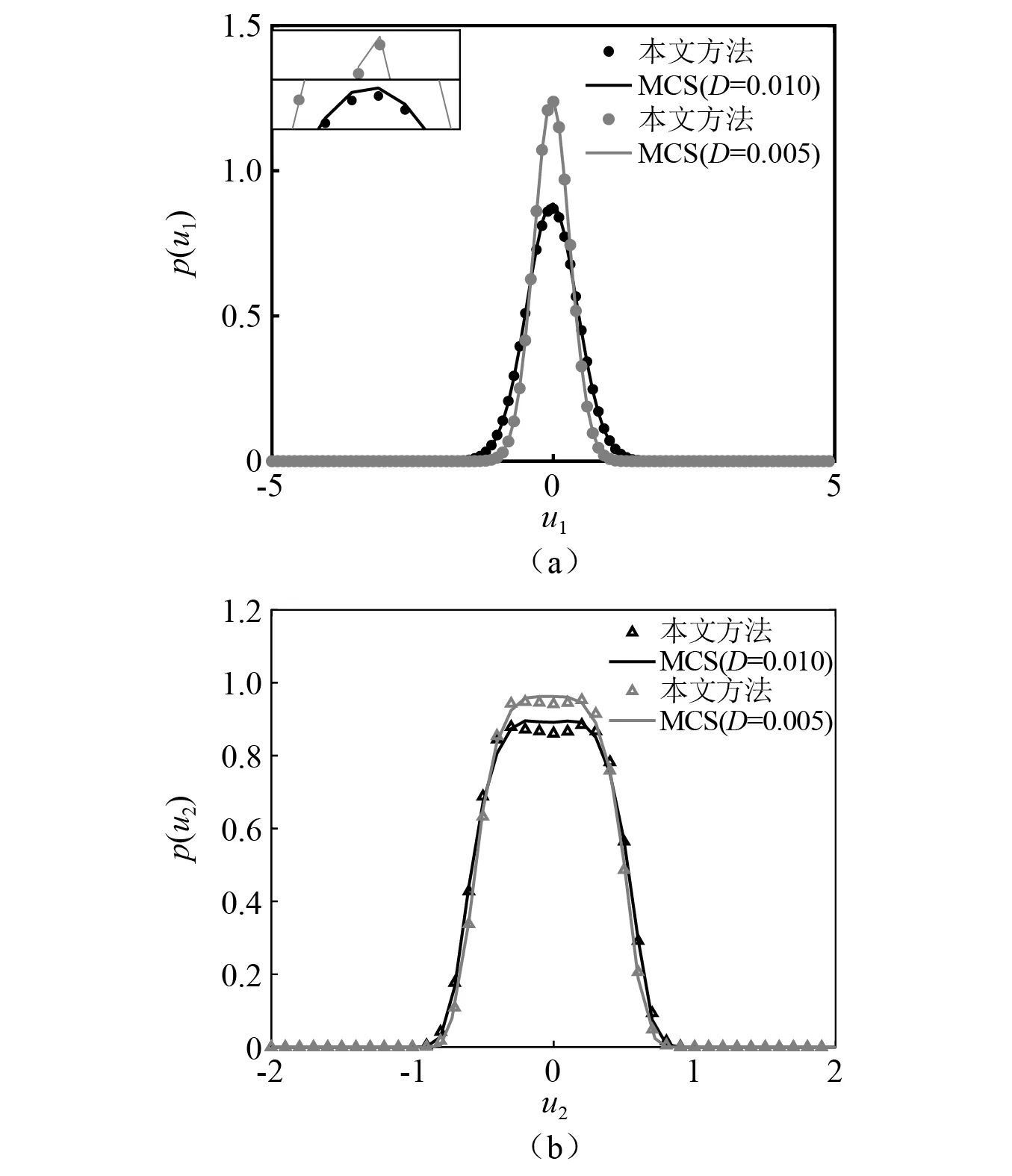
图2 不同激励强度时等价系统式(4)的边缘概率密度Fig.2 Themarginal PDF of equivalent system

在获得方程式(12)基础上，利用雅可比矩阵进一步获得原始系统稳态概率密度函数的近似表达式，即

(19)

式中，|J|为与式(3)相关的雅可比行列式。鉴于概率密度函数ρ完全描述了随机变量Xi(t)(i=1,2)响应的统计特性，并且具有解析的表达式，可为开展NES参数优化设计提供必要的条件。

3 NES的参数优化分析

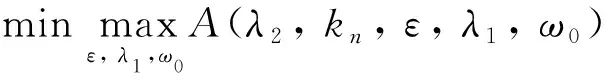
(20)

式中：Gi(i=1,2)分别为阻尼系数λ2和刚度系数kn的取值范围；λ2,kn,ε为设计变量；A(ε,ω0,λ1,λ2,kn)为NES减振效果的性能指标。请注意，式(20)中的问题无法用常规方法直接分析计算。但是，通过选取合适的目标函数，就能够把问题转化为一般的非线性优化问题，即

minσ(λ2,kn,ε,λ1,ω0)
subject to.λ2∈G1;kn∈G2

(21)

式中，σ为参数优化的目标函数。本文以主结构位移与速度响应量的均方为目标函数，NES控制参数的优化设计采用直接搜索法。算法流程如图3所示，所采用的优化步长和参数空间，如表1所示。

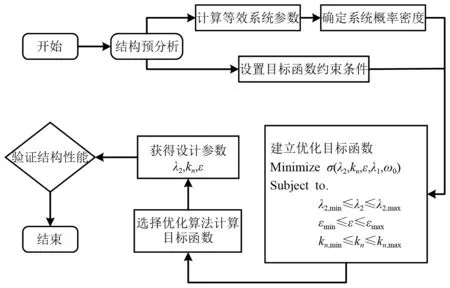
图3 参数优化流程图Fig.3 Flow chart for parameter optimization

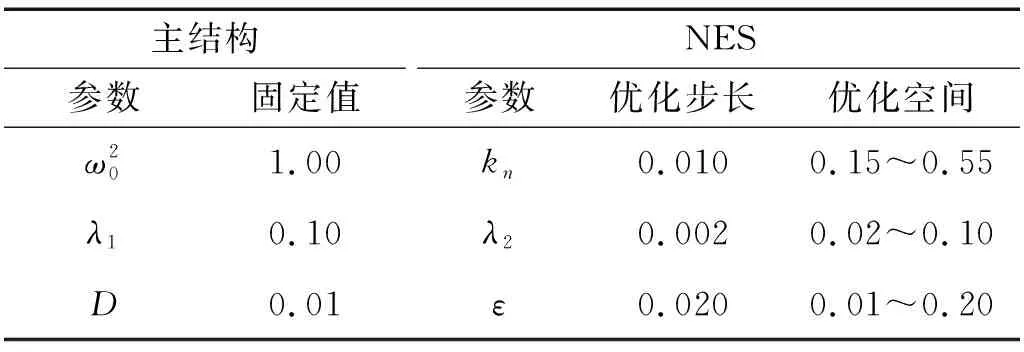
表1 NES参数优化条件Tab.1 Parameters of optimization condition

本节考察了阻尼系数λ2，刚度系数kn和质量比ε对NES减振性能的影响规律。不同质量比ε= 0.01,0.05和0.10时关于主结构位移与速度均方随λ2与kn的变化规律，如图4～图6所示。由图4～图6可知，关于位移均方和速度均方的变化趋势基本一致。λ2的增加能有效地降低主结构响应，即NES的减振性能随λ2的增加而提高。在给定的范围内，最佳值位于给定区间的边界处。增加质量比ε可以显著降低系统的均方响应值,即NES的减振性能会得到有效提高。针对非线性刚度值kn对NES的减振性能影响规律与质量比的取值相关。当质量比较小时，参见图4和图5，主结构均方响应随着非线性刚度值kn的增加，先减小后增加，即存在一个使均方响应保持在最低水平的最优非线性刚度区间。然而，当质量比取0.1时，见图6，主结构均方响应的变化规律与质量比较小情形存在明显差异，随着非线性刚度值kn的增加，主结构均方响应先增加达到一个最大峰值，随后开始衰减。因此，在质量比取较大值时，非线性刚度值kn的设计需谨慎，有可能加剧系统振动，降低NES的减振性能。

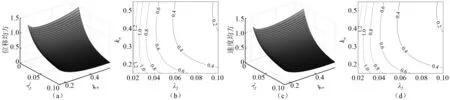
图4 当ε=0.01时主结构的位移与速度均方随λ2与kn的变化规律Fig.4 The change regularity of MS of displacement and velocity with λ2 and kn for ε=0.01

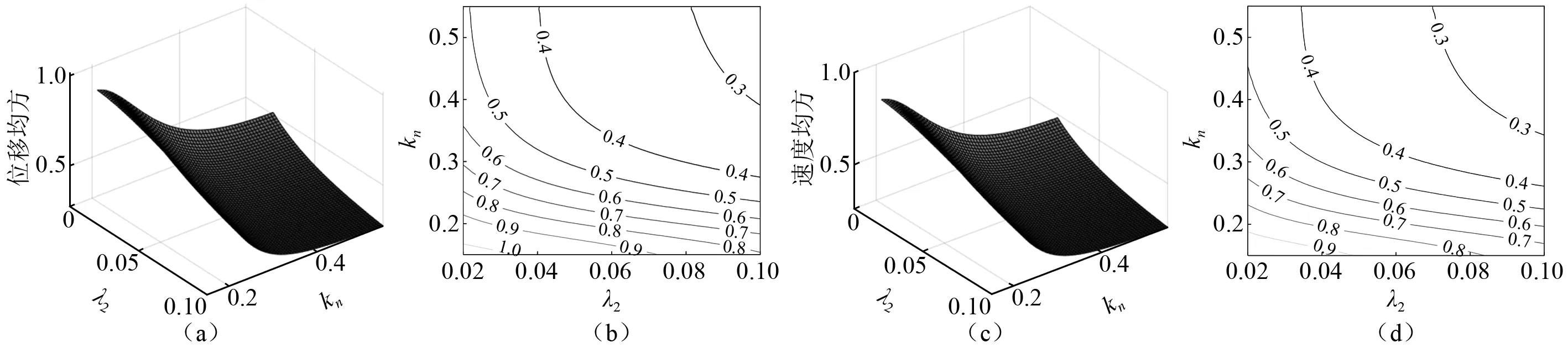
图5 当ε=0.05时主结构的位移与速度均方随λ2与kn的变化规律Fig.5 The change regularity of MS of displacement and velocity with λ2 and kn for ε=0.01

图6 当ε=0.1时主结构的位移与速度均方随λ2与kn的变化规律Fig.6 The change regularity of MS of displacement and velocity with λ2 and kn for ε=0.01

在最优参数NES、偏离参数优化值NES以及未控情形时(未耦合NES)系统主结构位移的瞬态与稳态响应概率密度函数的蒙特卡洛模拟结果，如图7所示。图7中：X1为主结构的位移响应；ρ(X1)为对应位移的概率密度。与无NES情形相比，处于最优NES参数与偏离优化值的NES参数情形下系统响应的概率密度显著降低，即两者均可有效地降低系统的响应，同时包括瞬态与稳态响应，但优化参数下的NES效果更为显著，也进一步表明本文提出的设计方法对于稳态与瞬态响应均有较好的效果。

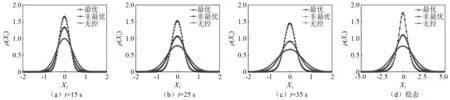
图7 不同时刻主结构位移响应概率密度函数的蒙特卡洛模拟结果Fig.7 The PDF of displacement of main structure at different time obtained with Monte Carlo simulation

4 结 论

本文针对高斯白噪声激励下耦合NES单自由度结构随机振动的参数优化问题提出了一种高效数值方法。应用加权残值法，将原系统等效为具有精确平稳解的随机动力学系统。理论解和蒙特卡洛模拟解在误差允许范围内吻合，显示所提的数值方法有效。在此基础上，利用原系统的平稳响应概率密度函数的近似解来构造主结构位移与速度响应量均方的目标函数，进行NES减振性能参数优化设计。综合分析了随机激励下NES的最优参数及其变化规律，得出以下主要结论：

(1) 在典型的高斯白噪声随机激励下，耦合NES结构的动力响应显著降低，表明NES能够有效实现结构振动控制的性能目标。通过选择有效结构参数能在较大程度上提高NES的减振性能。

(2) 参数研究表明，质量比ε与阻尼系数λ2的增大能有效提高NES的减振性能。非线性刚度kn在质量比较小时存在最优刚度区间，当质量比取到较大值时，kn的增大可能会引起系统振动恶化。

(3) 基于结构性能的NES参数设计方法，以主体结构位移和速度响应量的均方最小为优化目标，来衡量NES减振性能。在充分发挥NES在结构振动控制方面优势的同时，又能满足目标性能的要求。

(4) 本文所涉及的NES并不是唯一形式，根据不同的应用需求，各类型NES的振动控制有待深入研究。