基于多头自注意力机制和卷积神经网络的结构损伤识别研究
2023-01-03张健飞黄朝东王子凡
张健飞, 黄朝东, 王子凡
(河海大学 力学与材料学院,南京 210098)
为了保证工程结构的安全和正常使用,需要及时发现结构损伤并进行维修处理。基于振动的结构损伤识别方法利用结构的振动测试信号进行结构整体损伤状况检测,相较于传统的无损检测方法具有很大的优越性[1],但在实际应用过程中,会不同程度地遇到模型依赖性强、系统容错性差、易受环境影响等问题。人工神经网络由大量相互连接的简单神经处理单元组成,可以不依赖于模型,具有较强的容错性和鲁棒性以及学习联想能力等特征,因而在结构损伤识别领域受到了广泛的关注。人工神经网络用于结构损伤识别的基本原理就是通过建立特征参数与结构损伤状态之间的输入、输出映射关系来实现损伤识别。目前已经构建了许多结构动力特征作为神经网络的输入参数,如:固有频率[2]、振型[3]和模态曲率[4]等,然而这些人为设计的特征参数并不一定是最优的,难以在不同类型的损伤识别中都取得最优效果[5]。
以卷积神经网络(convolutional neural networks, CNN)为代表的深度学习网络可以直接从原始输入数据中挖掘抽象的内在特征,避免了人为主观因素的影响,具有良好的泛化能力。CNN是一类包含卷积计算的深度前馈神经网络,其所具有的局部连接、权值共享及池化操作等特性可以有效地降低网络的复杂度,减少训练参数的数目,从而使模型具有强鲁棒性和容错能力,已经在计算机视觉、语音识别等领域得到了广泛应用[6]。在结构损伤识别领域,近年来CNN也得到了较多的研究。罗雨舟等[7]通过构建CNN模型对有限元数值模拟生成的结构多点加速度信号进行特征提取,实现损伤诊断,并研究了结构在不同激励类型作用下和不同噪声强度下的损伤诊断精度。李雪松等[8]以IASC-ASCE SHM Benchmark结构的数值模拟数据为研究对象,用CNN直接从加速度信号中自动提取特征,并提出混合噪声训练模式,加强特征抗噪能力,取得了良好的识别效果。李书进等[9]以多层框架结构节点损伤位置的识别问题为研究对象,构建了基于原始信号和傅里叶频域信息的一维CNN模型和基于小波变换数据的二维CNN模型。Khodabandehlou等[10]以一座钢筋混凝土公路桥缩尺模型振动台试验测得的加速度信号作为输入数据,采用二维CNN对结构损伤进行识别,取得了很好的识别效果,并检验了网络对微小损伤的鲁棒性和敏感性。Lin等[11]采用CNN从简支梁有限元模拟生成的加速度数据中提取损伤特征,在有噪声情况和多损伤情况下取得了很高的损伤识别精度,同时通过隐层可视化对所提取的特征进行了物理解释。Liu等[12]将传递函数和一维CNN相结合对结构损伤识别方法进行了研究,并以ASCE Benchmark结构动力响应的传递函数作为CNN的输入数据,对方法的有效性进行了验证,通过与时间序列和FFT (fast Fourier transform)数据相比较,显示了传递函数数据中获取的特征具有更高的损伤敏感性。杨建喜等[13]提出一种联合CNN和长短期记忆网络(long-short term memory, LSTM)的桥梁结构损伤识别方法,以结构振动加速度响应为输入,通过 CNN 模型提取多时间窗口内传感器拓扑相关性特征,通过LSTM 模型进一步提取时间维度特征,并以某连续刚构桥缩尺模型的试验数据对方法进行了检验,取得了良好的效果。Yang等[14]将结构振动加速度信号作为多变量时间序列,并行输入CNN和双向门控循环单元提取数据特征,然后将这两种网络获得的特征进行组合后用于结构损伤识别,并通过数值试验和连续刚构桥缩尺模型试验验证了方法相较于CNN和LSTM等方法的优越性。
注意力机制本质上和人类视觉机制类似,其核心目标是从众多信息中选择出对当前任务目标更关键的信息,使得模型在训练过程中关注重点特征,避免非敏感特征的影响。自注意力机制是注意力机制的一种变体,用于捕捉数据或特征自身内部的相关性。多头自注意力机制最初被用于机器翻译,它通过对多次计算得到的自注意力特征的组合,实现不同位置处的数据在不同子空间中的表征,从而使得模型可以在多个不同表征子空间中学习到相关的信息[15]。
本文以结构振动加速度信号作为输入数据,联合多头自注意力机制和CNN,提出了一种基于多头自注意力的CNN模型(multi-head self-attention based CNN,CNN-MA),通过CNN提取加速度信号中的局部特征,通过引入多头自注意力机制,在多个不同表征子空间中抽取出信号中重要的全局信息,提高结构损伤识别的效果。
1 基于多头自注意力的CNN模型
本文构建的基于多头自注意力的CNN模型依次由输入层、若干个卷积和池化层、多头自注意力层、全局池化层和Softmax分类层堆叠组成,如图1所示。模型中输入层输入结构受到动力作用后各个测点上产生的加速度信号;卷积层和池化层提取输入加速度信号中的短期局部特征并实现降维;多头自注意力层通过关注池化层输出序列在不同位置、不同表征子空间中的关键信息,学习长期全局特征;全局池化层对序列各个位置的信息进行汇总并压缩;最后将全局池化层的输出经过全连接层后再通过Softmax进行分类,类别数对应损伤模式的个数,每个神经元输出对应不同损伤模式的发生概率,最大发生概率对应的损伤模式即为预测的损伤模式。为了分析CNN-MA的性能,本文与CNN、CNN-LSTM和CNN-BiLSTM(bidirectional LSTM)等模型进行了比较,各模型结构见图1。
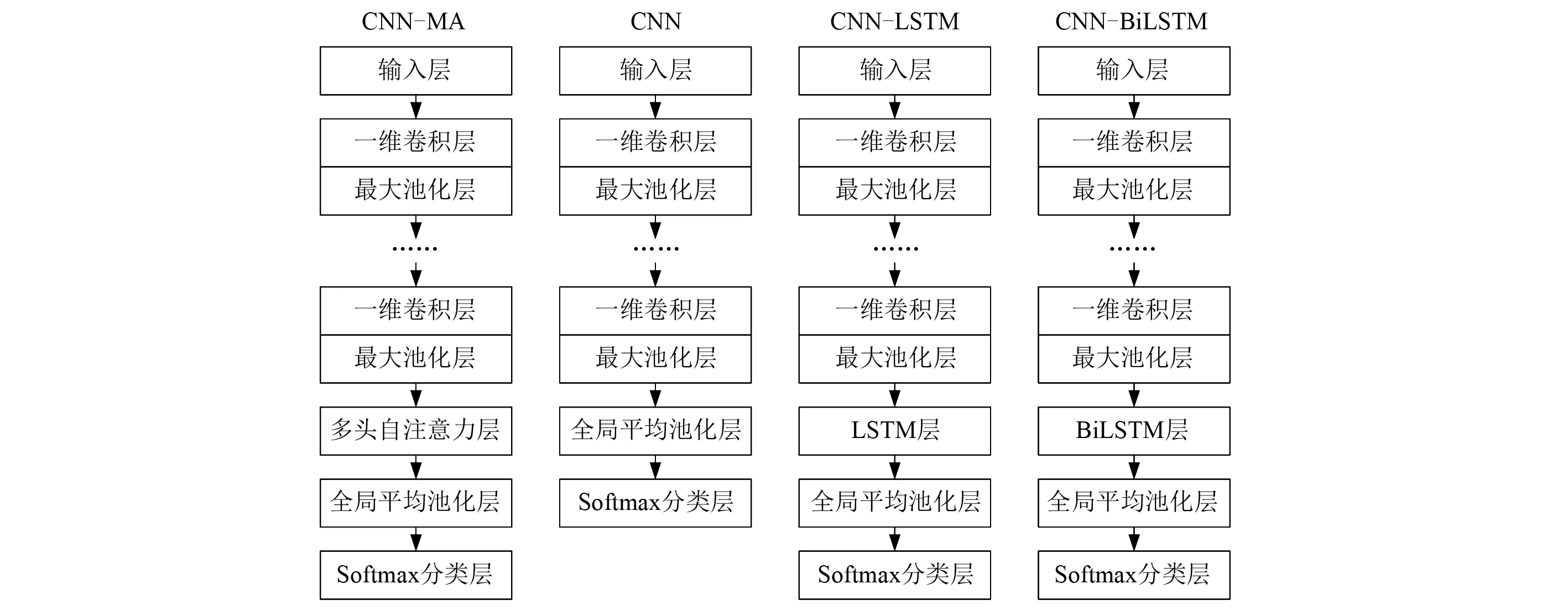
图1 模型结构Fig.1 Structure of the models
1.1 输入层
本文直接以结构在外界动力荷载作用下的测点加速度信号作为输入数据,由于是多测点问题,因此输入数据可以看作向量时间序列fi(i=1,2,…,N)。其中fi=(fi,1,fi,2,…,fi,L)为L个测点在时刻i的加速度值组成的向量,序列长度N=测试时长×采样频率。在输入模型之前,输入的加速度信号需要进行样本化和标准化处理。样本化就是将测点加速度信号序列分割成长度为T的若干段子序列si(i=1,2,…,T),作为模型的训练和测试样本,T的取值一般至少使得样本包含一个结构特征自振周期的加速度采样值。生成样本后,本文对样本进行Z-Score标准化,其计算如式(1)所示。
(1)
式中:μ为时间序列si(i=1,2,…,T)的均值;σ为标准方差。
1.2 卷积层和池化层
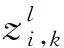
(2)
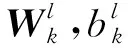
(3)
典型的激活函数有sigmoid、tanh和ReLU等,本文采用ReLU激活函数。

(4)
式中,Ri为第i个位置处数值周边的邻近区域,常见的池化操作有取平均值和取最大值,本文采用最大池化。
通过卷积和池化计算得到的CNN输出序列数据为xi(i=1,2,…,M),其中xi=(xi,1,xi,2,…,xi,P),P为最后一层卷积层的特征图个数,输出序列的长度M由卷积核尺寸、池化尺寸和步长等参数具体确定。
1.3 LSTM层
LSTM是循环神经网络(recurrent neural networks, RNN)的一种变体,主要用于处理序列数据,能够保持数据中的时序依赖关系。它通过引入了门控单元,解决了普通RNN长程依赖、梯度消失或梯度爆炸等问题,已经在自然语言处理等领域得到成功应用。LSTM使用记忆细胞来代替一般网络中的隐藏层细胞,记忆细胞的输入和输出都由一些门控单元来控制,这些门控单元控制流向隐藏层单元的信息。其中:遗忘门决定从上一个细胞状态中遗忘什么信息,输入门将新的信息选择性的记录至细胞状态中,输出门将信息传递出去。本文采用的LSTM网络细胞结构,如图2所示。
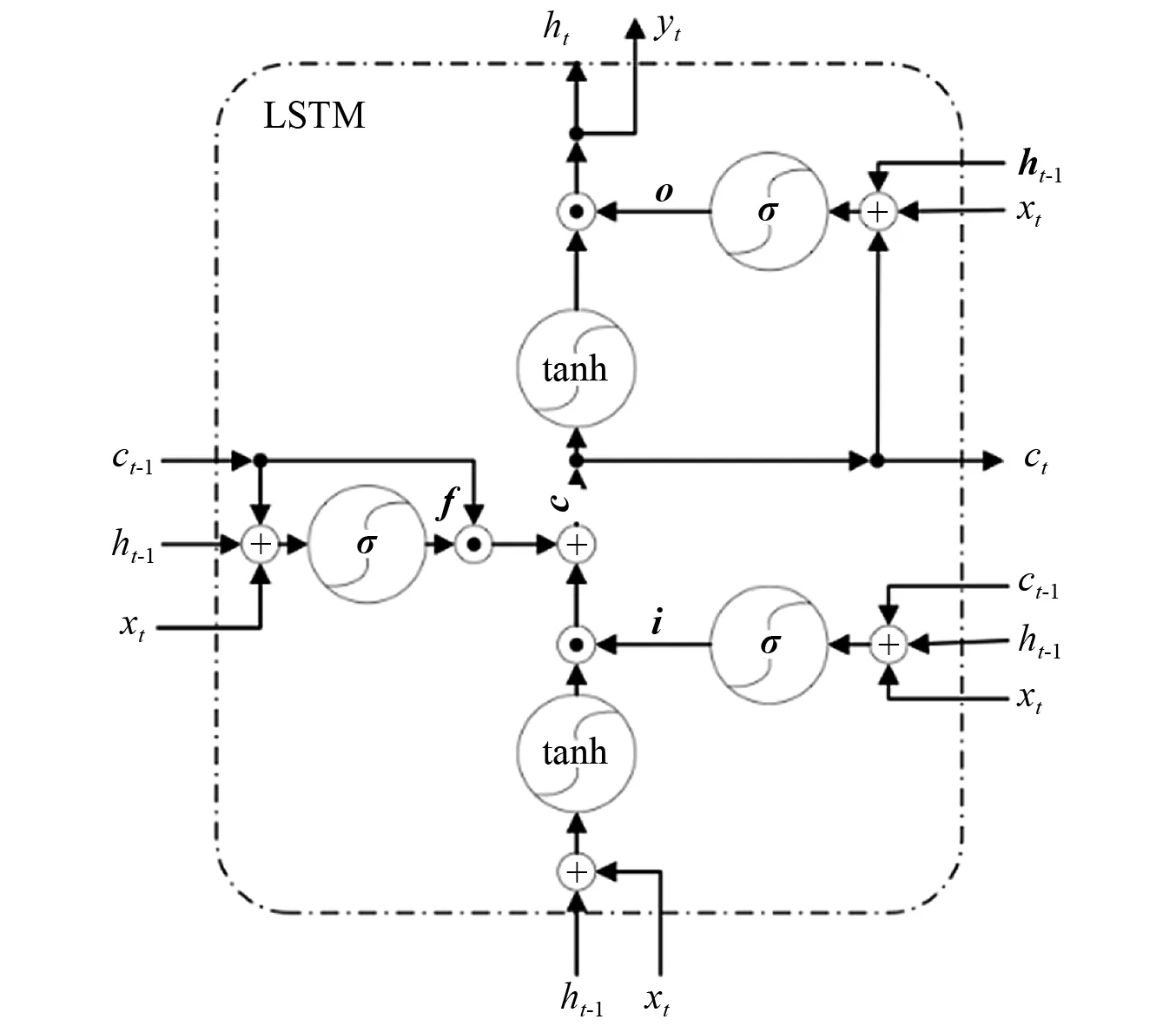
图2 LSTM细胞结构Fig.2 Structure of LSTM cell
图2中的i,f,c,o,h分别为输入门、遗忘门、细胞状态、输出门以及隐藏层的输出向量,其计算方法如式(5)~式(9)所示。
it=σ(Wxixt+Whiht-1+Wcict-1+bi)
(5)
ft=σ(Wxfxt+Whfht-1+Wcfct-1+bf)
(6)
ct=ftct-1+ittanh(Wxcxt+Whcht-1+bc)
(7)
ot=σ(Wxoxt+Whoht-1+Wcoct+bo)
(8)
ht=ottanh(ct)
(9)
式中:下标x,i,f,c,o,h分别为输入层、输入门、遗忘门、细胞状态、输出门以及隐藏层;W和b分别为对应的权重矩阵以及偏置;t为时刻。
通过LSTM层计算得到的输出序列数据为oi(i=1,2,…,M),其中oi=(oi,1,oi,2,…,oi,D),D为输出门维度。
在有些问题中,当前时刻的输出不仅和之前的状态有关,还可能和未来的状态有关系。此时可以采用双向LSTM(bidirectional LSTM, BiLSTM),将输入序列按照正序和反序分别输入LSTM,然后将正向和反向LSTM的输出相结合作为最终的输出,常用的结合方式有求和、求积、平均和拼接等,本文采用拼接的结合方式,此时的输出向量维度为2D。
1.4 多头自注意力层
注意力可以描述为查询向量和一系列键-值向量对与输出向量之间的映射,其中:输出向量通过值向量的加权求和得到,每个值向量的加权系数通过计算查询向量与对应的键向量之间的匹配度而得到,本文中的加权系数通过计算查询向量和键向量之间的尺度化点积得到。当查询向量、键向量和值向量属于相同的序列时称为自注意力。对于一系列查询向量的注意力计算,通常为了提高计算效率将查询向量、键向量和值向量组合成查询矩阵、键矩阵和值矩阵进行运算,如式(10)和图3所示。多头自注意力层首先采用不同的线性投影矩阵将维度为M×d的输入矩阵映射为h组矩阵,每组矩阵包含3个不同的矩阵:查询矩阵Q、键矩阵K和值矩阵V,矩阵Q和K的维度为M×dk,矩阵V的维度为M×dv。然后对这h组矩阵分别按照式(10)进行自注意力运算,最后将自注意力运算得到的h个输出矩阵拼接后投影为一个维度为M×d的输出矩阵R,如式(11)和图4所示。
(10)
R=Multihead(Q,K,V)=
Concat(head1,head2,…,headh)Whr
(11)
式中,线性投影矩阵Whr∈hdv×d。
多头自注意力层输出数据为ri(i=1,2,…,M),其中向量ri=(ri,1,ri,2,…,ri,d)。
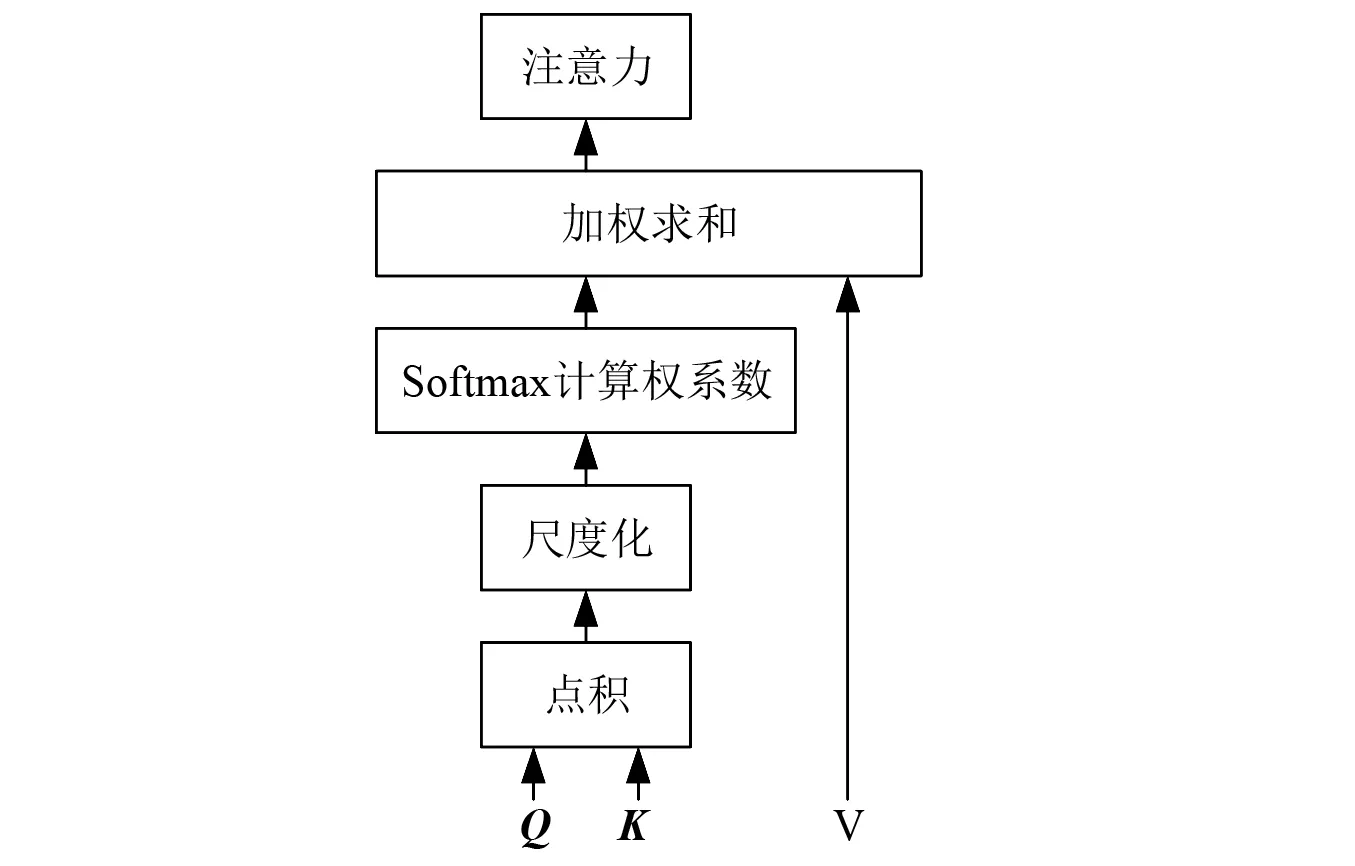
图3 尺度化点积注意力Fig.3 Scaled dot-product attention
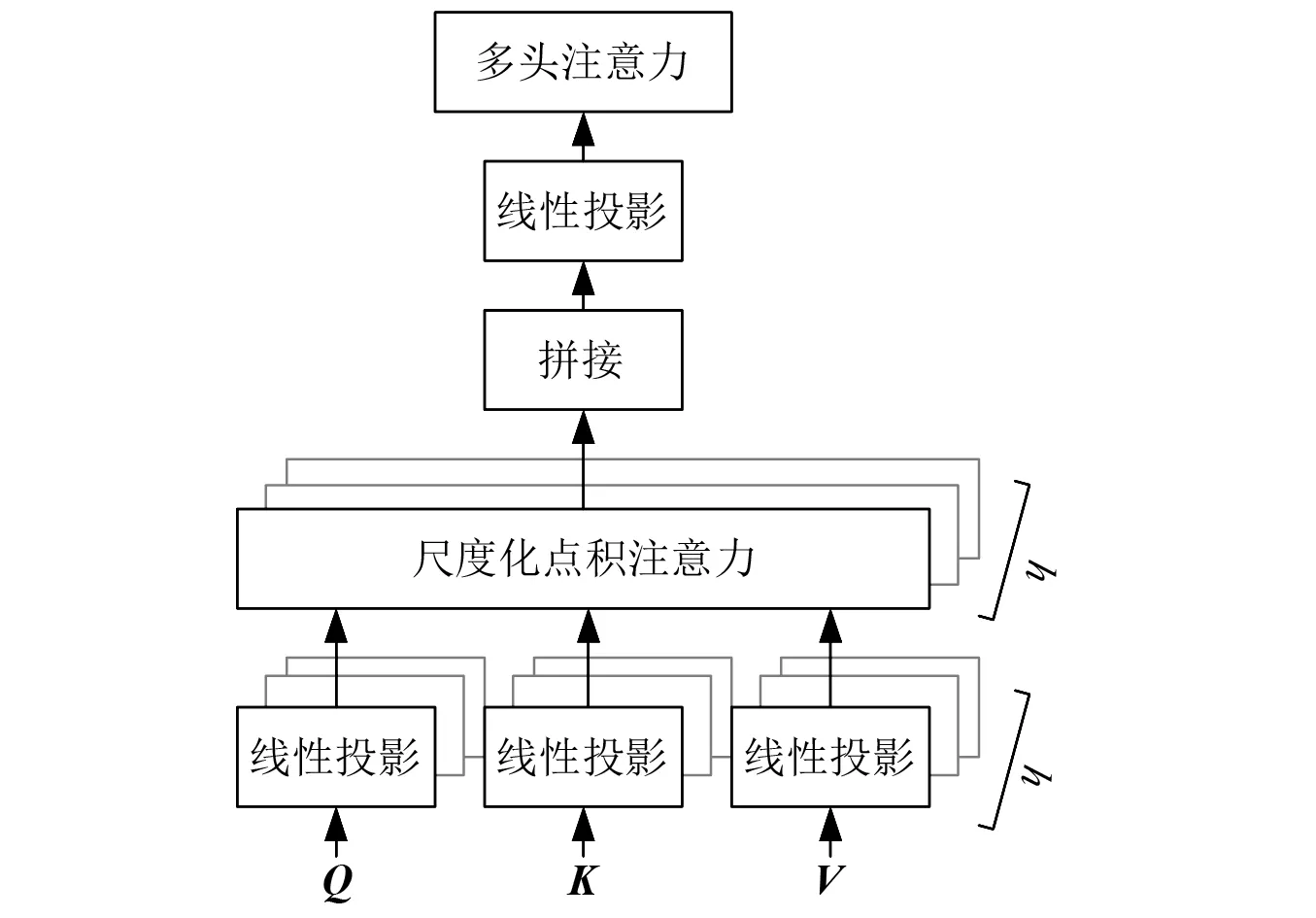
图4 多头注意力Fig.4 Multi-head Attention
1.5 全局池化层
全局池化一般分为全局最大池化和全局平均池化,全局池化可以起到减少参数、防止过拟合的作用。本文采用全局平均池化,即计算向量时间序列中向量各个元素在时间域上的平均值,如式(12)所示,得到输出向量g=(g1,g2,…,gD)。
(12)
1.6 Softmax分类层
最后将全局池化层的输出向量输入全连接层后再通过Softmax进行分类,类别的数量等于损伤模式的个数nd。Softmax分类层将输入数据转化为一个概率分布,其计算如式(14)所示,然后根据概率最大的原则进行模式识别。
g′=Wgg′g
(13)
(14)
式中,全连接层的权重系数矩阵Wgg′∈nd×D。
1.7 基于CNN-MA的结构损伤识别
本文提出的基于CNN-MA的结构损伤识别方法首先采集结构上各个测点的振动加速度信号;然后将这些加速度信号进行预处理,即对其进行标准化后分割成一系列具有一定长度的子信号;再将这些子信号及其对应的损伤状态按照一定的比例划分成训练集、验证集和测试集;采用训练集进行模型的训练,采用验证集进行模型的验证,根据验证结果进行模型结构和超参数的优化;最后将测试集输入训练好的模型进行损伤识别,测试模型泛化性能。整个结构损伤识别的流程如图5所示。本文基于其他模型的结构损伤识别流程与CNN-MA相同。
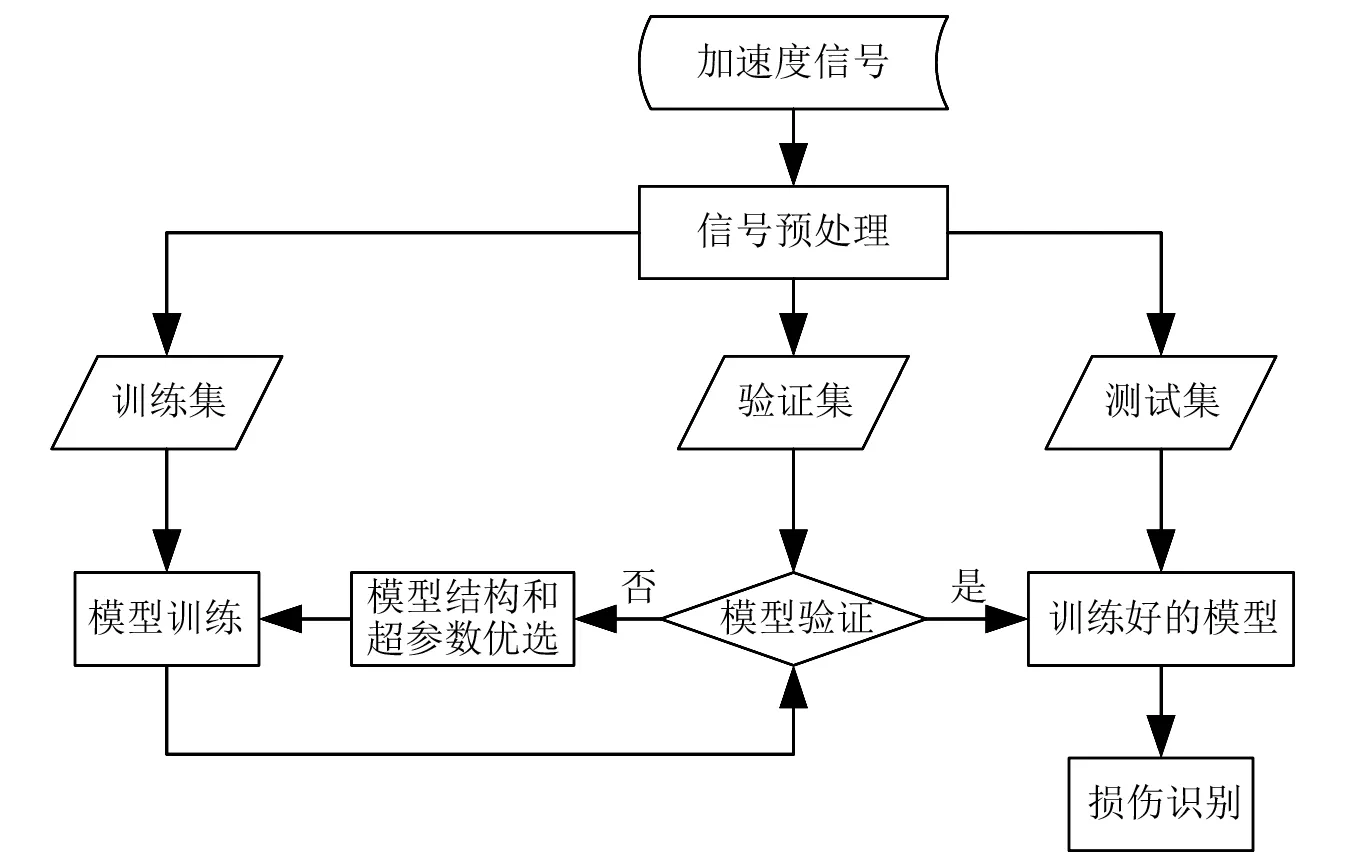
图5 结构损伤识别流程图Fig.5 Flow chart of structural damage identification
由式(2)可知,CNN隐藏层中每一个神经元只与相邻层局部区域的神经元相连,这个局部区域被称为局部感受野,也就是某一个隐藏层中神经元只学习了其局部感受野范围内的特征,而要学习整个序列的全部特征,需要堆叠多个隐藏层,从而使得CNN模型变得复杂,训练难度变大。将CNN与LSTM(BiLSTM)相结合的目的就是通过LSTM(BiLSTM)将当前时刻之前(之后)的信息压缩后传递给当前时刻,从而能够获取全局特征,但是这种信息压缩会一定程度上导致有用信息的丢失。而CNN-MA将卷积池化层输出序列中每一个向量与序列中的全部向量进行自注意力运算,从而使得每个向量中除了包含局部特征也包含全局特征。
2 试验验证
2.1 数值试验
2.1.1 数据生成与预处理
为了测试CNN-MA模型的性能,本文首先建立了一个悬臂梁有限元模型进行数值试验,悬臂梁材质为钢材,长1 200 mm,方形截面尺寸为20 mm×20 mm,底部为固定端,顶部为自由端。在悬臂梁一侧不同高程处设置深2 mm的水平裂缝(记为C1~C6)模拟不同位置的损伤,另一侧设置7个测点(记为m1~m7)记录悬臂梁水平向加速度,悬臂梁裂缝位置和测点位置如图6所示。每种损伤模式为不同位置处的单个裂缝,如表1所示。
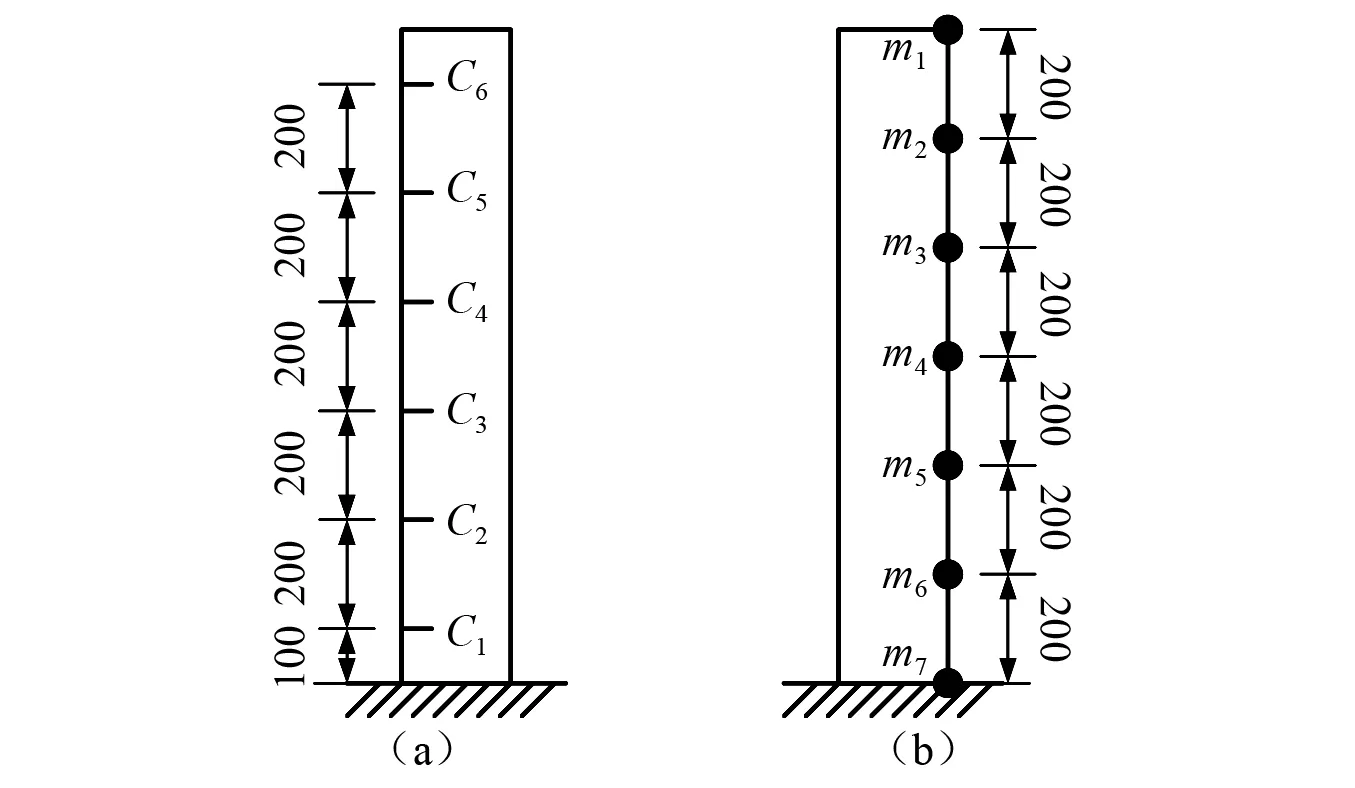
图6 悬臂梁裂缝位置和测点图(mm)Fig.6 Positions of the cracks and accelerometers on the cantilever beam (mm)
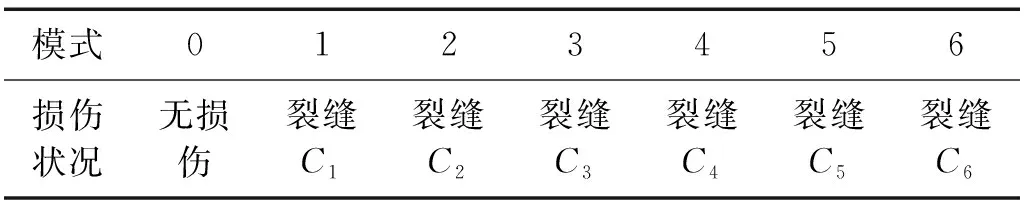
表1 数值试验中悬臂梁的损伤模式Tab.1 Damage patterns of the cantilever beam in numerical test
通过在悬臂梁底部施加水平向白噪声加速度模拟环境激励,按照表2所示的损伤情况,生成7种不同损伤模式下7个测点上时长为30 s的加速度响应信号,有限元计算时间步长取为0.000 1 s,采用Rayleigh阻尼,则每种损伤模式可得到一个长度为300 000、维度为7的加速度信号序列。然后从每个信号序列中随机抽取1 000个长度为1 024、维度为7的子序列作为模型的输入样本序列,共得到7×1 000=7 000个样本序列。
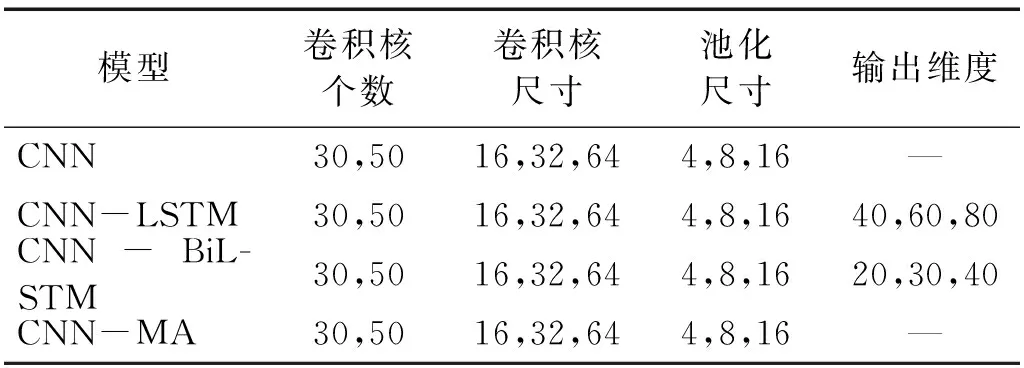
表2 各个模型超参数取值范围Tab.2 Range of the hyper-parameters of the models
在实测信号中,噪声总是存在的,这些噪声一般可以假设为符合高斯分布的白噪声[16]。本文在有限元计算得到的加速度信号中加入白噪声数据来模拟实测信号,即
(15)
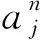
2.1.2 模型结构和参数
神经网络模型的结构和超参数对其性能具有很大的影响,为了获取较优的网络结构和超参数,本文在beam-n00数据集上采用网格搜索的方法比较了各个模型在不同网络结构下多种超参数组合的性能,各模型的超参数取值范围,见表2。模型超参数优选时的性能指标采用5-折交叉验证确定,即将数据集平均分成5组,其中每一组子集数据分别作为验证集,其余的4组子集数据作为训练集,以得到的5组验证集上的损伤识别准确率的平均值作为模型性能评价的指标。
对于CNN模型,比较了包含2个卷积池化层的网络结构(2层结构)和包含3个卷积池化层的网络结构(3层结构)在卷积核数量、卷积核尺寸和池化尺寸3个超参数的不同组合下的损伤识别性能,每种结构共计18种超参数组合,比较结果如表3所示。可以看出:在本例中不同的超参数组合对识别准确率的影响较大,过大的卷积核尺寸会导致识别失败,增加卷积池化层数量反而会降低识别准确率;当CNN模型采用2层结构,卷积核数、卷积尺寸和池化尺寸分别取30,32和4时损伤识别准确率最高。
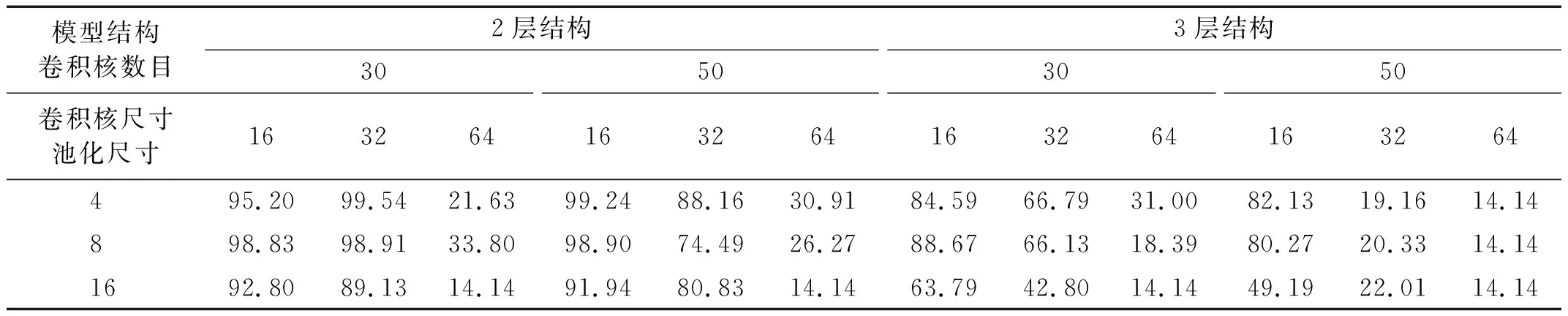
表3 CNN在不同结构和超参数组合下的识别准确率Tab.3 Accuracy of CNN with different structures and hyper-parameters 单位:%
对于CNN-LSTM和CNN-BiLSTM模型,比较了包含一个卷积池化层的网络结构(1层结构)和包含2个卷积池化层的网络结构(2层结构),每一种结构比较了卷积核数量、卷积核尺寸、池化尺寸和LSTM(BiLSTM)输出维度4个超参数不同组合下的损伤识别性能,共计54种超参数组合,比较结果如表4和表5所示。可以看出:1层结构和2层结构在本例中的识别准确率总体上差别不大,但是同种结构在不同超参数组合下差异较大;CNN-LSTM模型采用1层结构,卷积核数量、卷积核尺寸、池化尺寸和输出维度分别取30,64,8和40时识别准确率达到最大;CNN-BiLSTM模型采用1层结构,卷积核数量、卷积核尺寸、池化尺寸和输出维度分别取50,32,8和40时识别准确率达到100%。
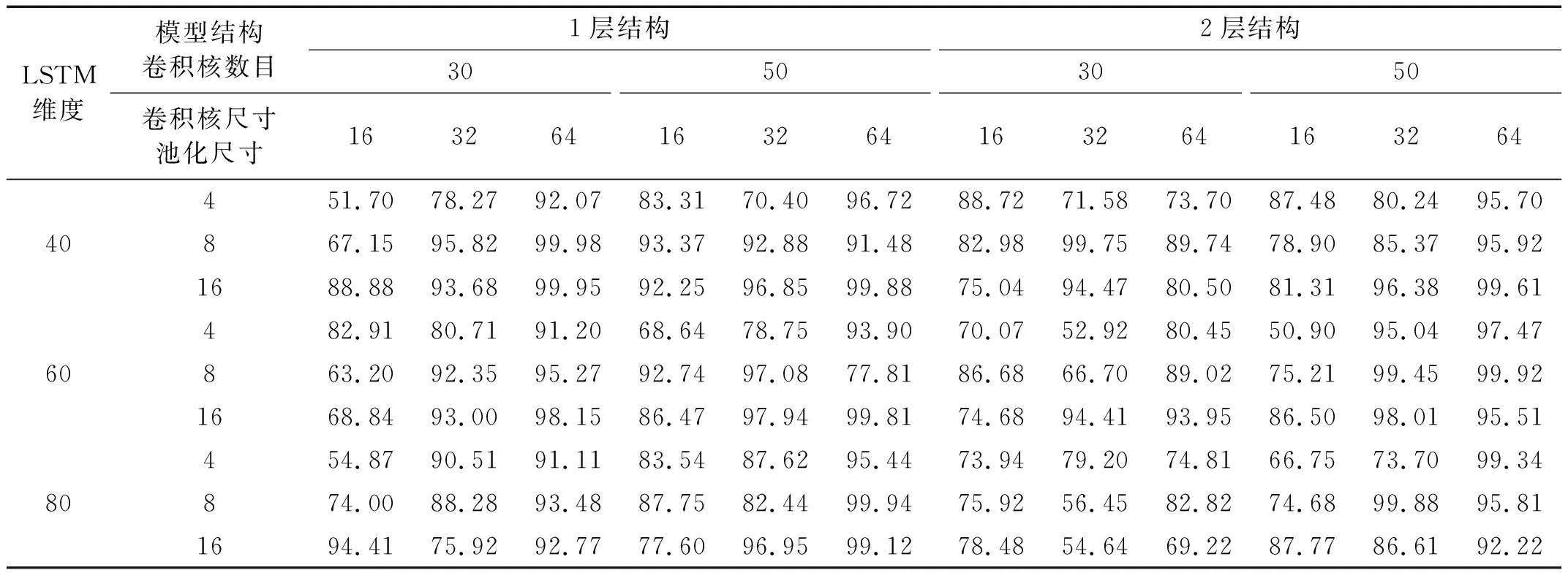
表4 CNN-LSTM在不同结构和超参数组合下的识别准确率Tab.4 Accuracy of CNN-LSTM with different structures and hyper-parameters 单位:%
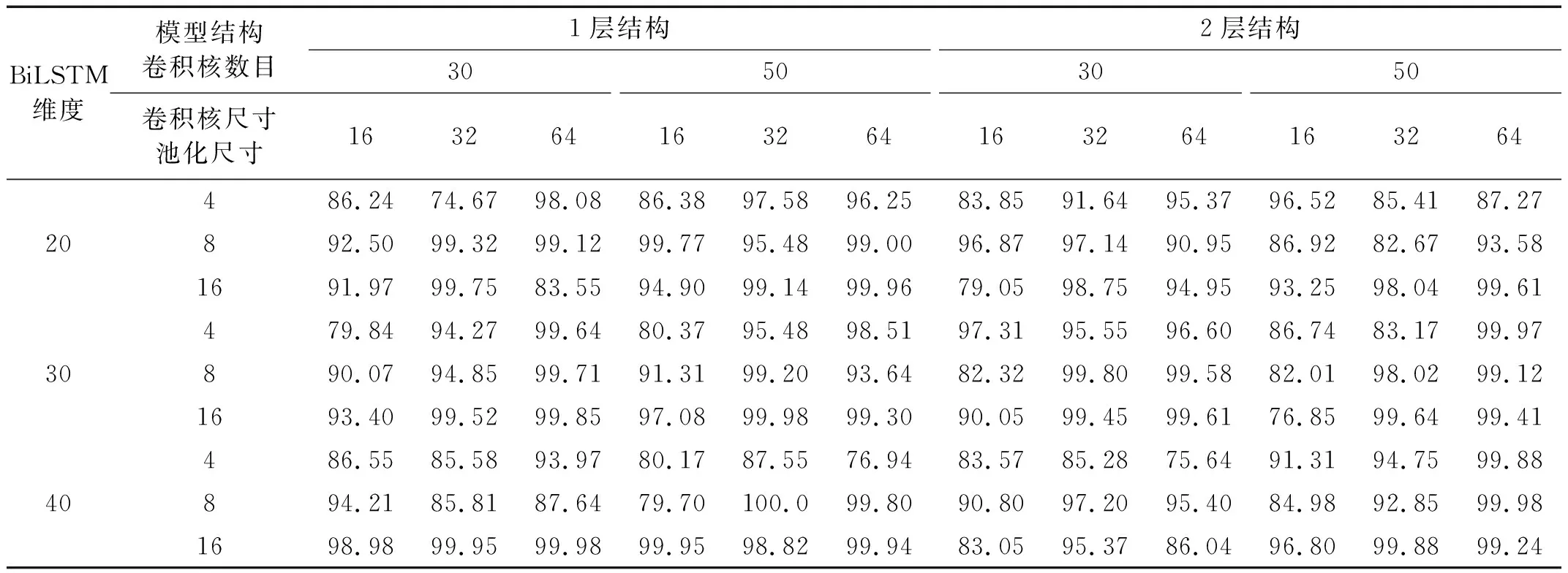
表5 CNN-BiLSTM在不同结构和超参数组合下的识别准确率Tab.5 Accuracy of CNN-BiLSTM with different structures and hyper-parameters 单位:%
对于CNN-MA模型,比较了包含1层卷积池化层的网络结构(1层结构)和包含2层卷积池化层的网络结构(2层结构)在卷积核数量、卷积核尺寸和池化尺寸3个超参数不同组合下的损伤识别性能,共计18种超参数组合,比较结果如表6所示。随后以较优的网络结构和超参数为基础,比较了模型自注意力计算次数分别取1,2,3,5和10时的损伤识别性能,比较结果如表7所示。可以看出:增加卷积池化层在本例中不能提高识别准确率,不同超参数组合对模型性能有较大影响,模型采用1层结构时多个超参数组合的识别准确率达到100%,其中卷积核数量、卷积核尺寸和池化尺寸3个超参数分别取30,32,4时不仅识别准确率达到最大,而且模型最为简单,在此基础上自注意力计算次数取3和5时识别准确率均达到100%。
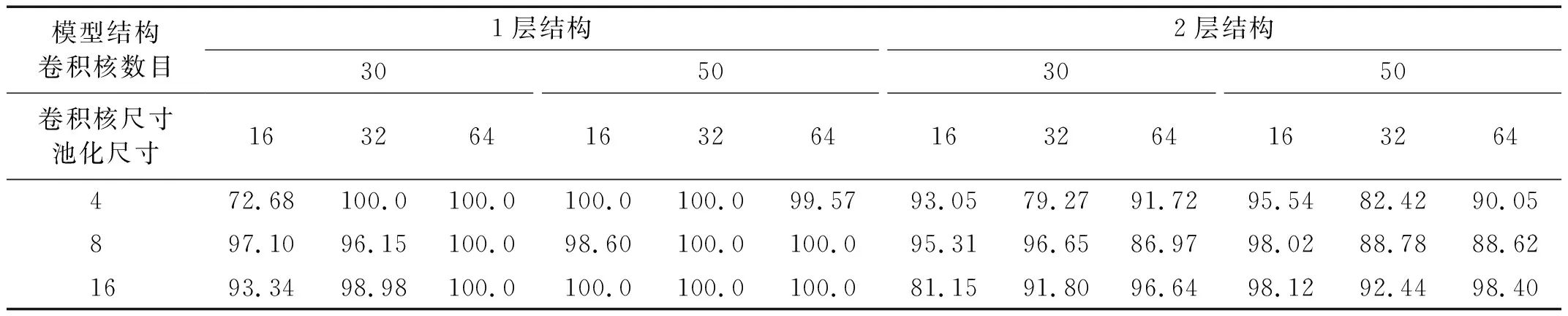
表6 CNN-MA在不同结构和超参数组合下的识别准确率Tab.6 Accuracy of CNN-MA with different structures and hyper-parameters 单位:%

表7 不同自注意力计算次数下的识别准确率Tab.7 Identification accuracy using different number of heads 单位:%
根据以上各个模型结构和超参数的比选结果,综合考虑识别准确率和计算效率选定各个模型较优的结构和超参数。CNN-MA模型的第1层是输入层,对数据进行预处理后输入模型;第2层是一维卷积和池化层,包含30个尺寸为32的卷积核和尺寸为4的最大池化层;第3层是多头自注意力层,其中查询向量、键向量和值向量的维度均为10,自注意力计算次数为3;第4层是全局平均池化层;第5层是Softmax分类层,类别数对应损伤模式的个数,每个输出对应不同损伤模式的发生概率。除了与CNN-MA模型相同的输入层、全局池化层和Softmax分类层外,CNN模型包含2层一维卷积和池化层,每一层包含30个尺寸为32的卷积核和尺寸为4的最大池化层;CNN-LSTM模型包含一层由30个尺寸为64的卷积核和尺寸为8的最大池化层组成的一维卷积池化层以及输出维度为40的LSTM层;CNN-BiLSTM模型包含一层由50个尺寸为32的卷积核和尺寸为8的最大池化层组成的一维卷积池化层以及正反向输出维度为40、拼接后的最终输出维度为80的BiLSTM层。
各模型训练时批尺寸设为64,训练次数设为50次,训练时保存训练过程中的最优模型用于损伤识别。各模型在本例中的需要学习的参数个数,如表8所示,其中MA-CNN模型参数最少。由于模型越复杂、参数越多,越容易过拟合,因此对于复杂的模型需要更多的训练数据或者采用正则化等技术抑制过拟合的发生,本文提出的MA-CNN模型由于参数更少,因此更加容易训练、泛化性能更好。
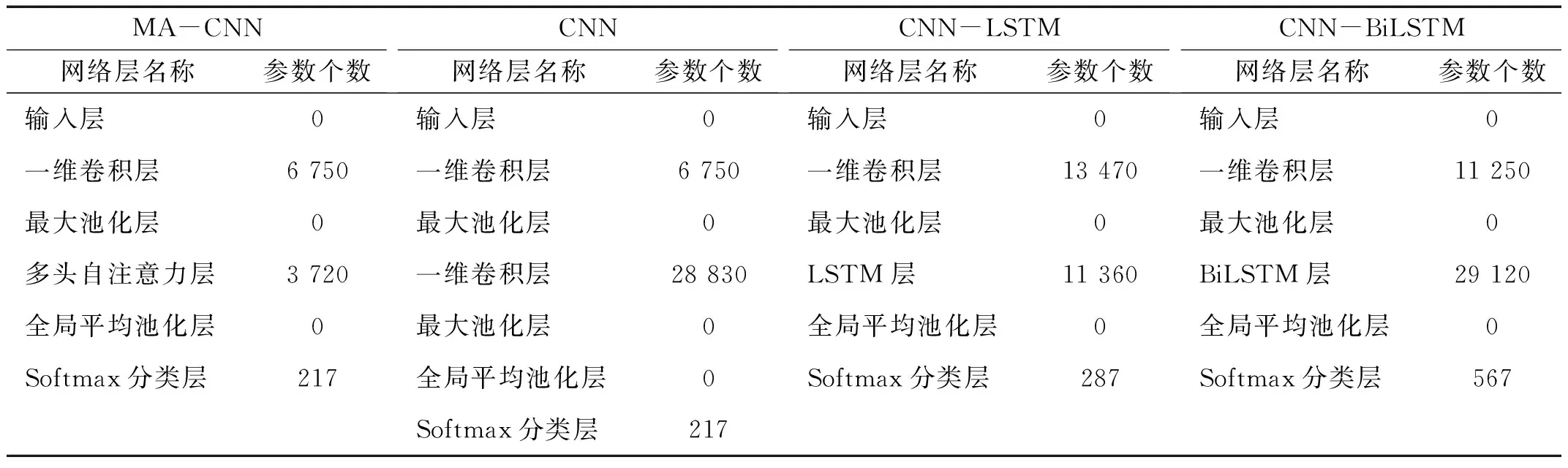
表8 各模型参数数量Tab.8 Number of the parameters of the models
2.1.3 试验结果
将样本按照8∶1∶1的比例划分,分别作为模型的训练集、验证集和测试集,训练集和验证集用于模型的训练,测试集用于测试模型的泛化性能。各个模型在训练集和验证集上的训练曲线,如图7~图9所示,图7~图9中:横坐标epoch为训练次数,纵坐标accuracy为训练准确率。可以看出:各个模型在训练集和验证集上的训练曲线基本吻合,未出现过拟合现象;在无噪声数据上各模型的训练准确率都达到100%,随着噪声的增大,各个模型准确率在训练集、验证集和测试集上仍能保持较高水平,但均有所下降;CNN-MA模型的收敛速度最快,其余模型收敛较慢,各模型都出现了不同程度的震荡现象,但是CNN-MA最稳定,这是因为CNN-MA模型复杂度最小,易于训练。各个模型在不同噪声水平数据集上的准确率,如表9所示。由表9可知:随着噪声水平的提高,CNN-MA的准确率最高,其次是CNN-LSTM和CNN-BiLSTM,CNN的准确率最低。为了进一步检验各模型的泛化性能,本文在测试集的每一种损伤模式下随机抽取了100个样本,用于测试各个模型的损伤识别性能。各个模型在测试集各种损伤模式下的识别性能,如表10所示。由表10可知:根据概率最大损伤判别法则,各个模型在本例数据集上均能准确识别出7种不同的损伤模式,说明各模型均具有较好的抗噪性;随着噪声水平的提高,各个模型的损伤识别精度存在不同程度的下降,CNN-MA模型受噪声影响程度最小,抗噪性最好,其次是CNN-LSTM和CNN-BiLSTM,CNN的识别准确率受到噪声影响最大。

图7 各模型在无噪声数值试验数据上的训练曲线FIg.7 Training curves of the models on numerical test data without noise
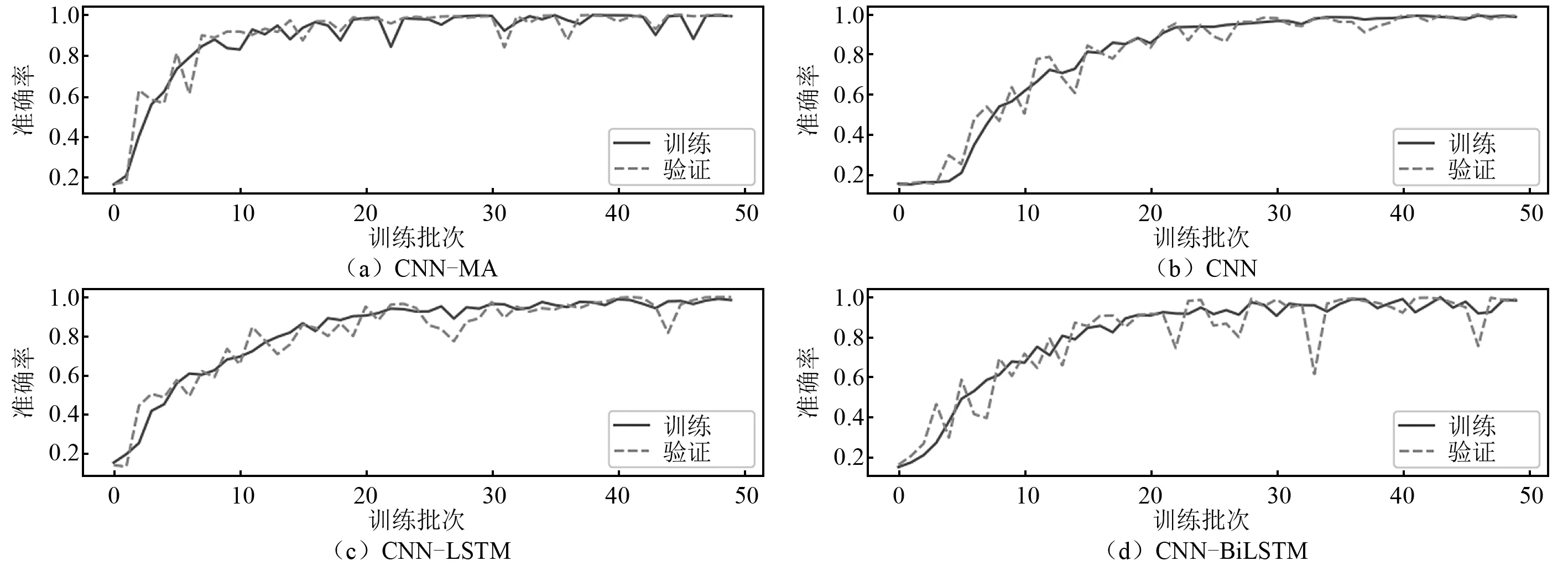
图8 各模型在含2%噪声数值试验数据上的训练曲线FIg.8 Training curves of the models on numerical test data with 2% noise
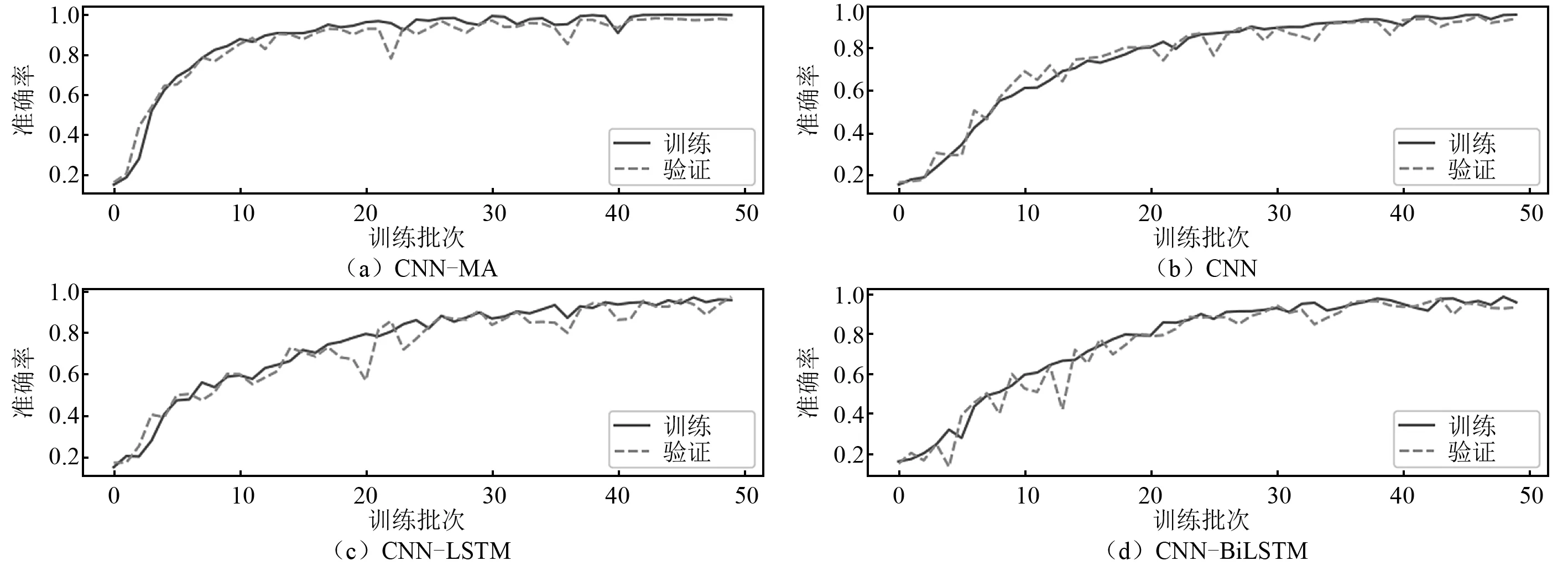
图9 各模型在含5%噪声数值试验数据上的训练曲线FIg.9 Training curves of the models on numerical test data with 5% noise

表9 各模型在悬臂梁数值试验数据上的准确率Tab.9 Accuracy of the Models on numerical test data of cantilever beam 单位:%
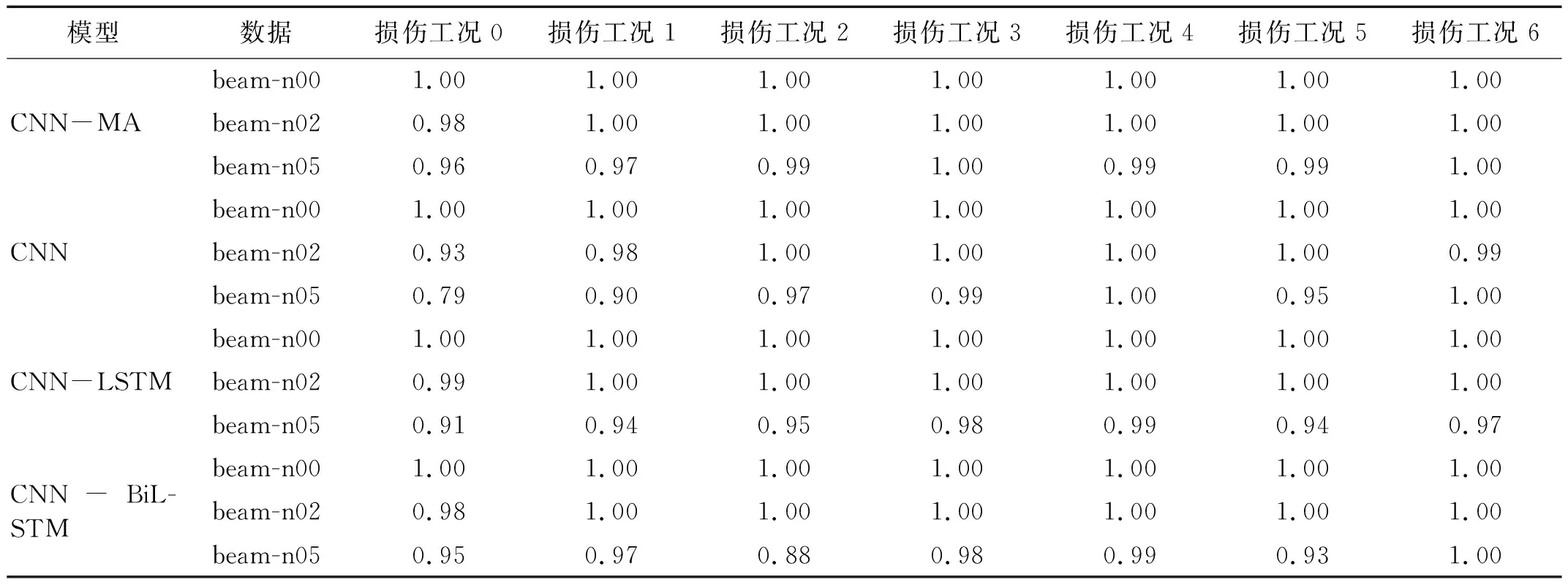
表10 各模型在悬臂梁数值试验测试集上的损伤识别概率Tab.10 Damage identifying probability of the models on numerical test data of cantilever beam
2.2 振动台试验
为了进一步验证方法的有效性,本文利用实验室中的悬臂梁振动台试验数据对模型进行测试和比较。试验所选用的悬臂梁材料和几何参数以及边界约束条件同第2.1节,损伤采用人工切割缝模拟,包括不同裂缝数量和不同裂缝深度等5种损伤模式,如表11所示。试验采用电动振动台产生的随机激励模拟有限带宽白噪声振动,激励的功率谱密度取0.1(m/s2)2/Hz,激振频率带宽为5~1 000 Hz。悬臂梁从自由端到固定端布置7个加速度传感器采集悬臂梁水平加速度,测点布置见图6,试验装置如图10所示。
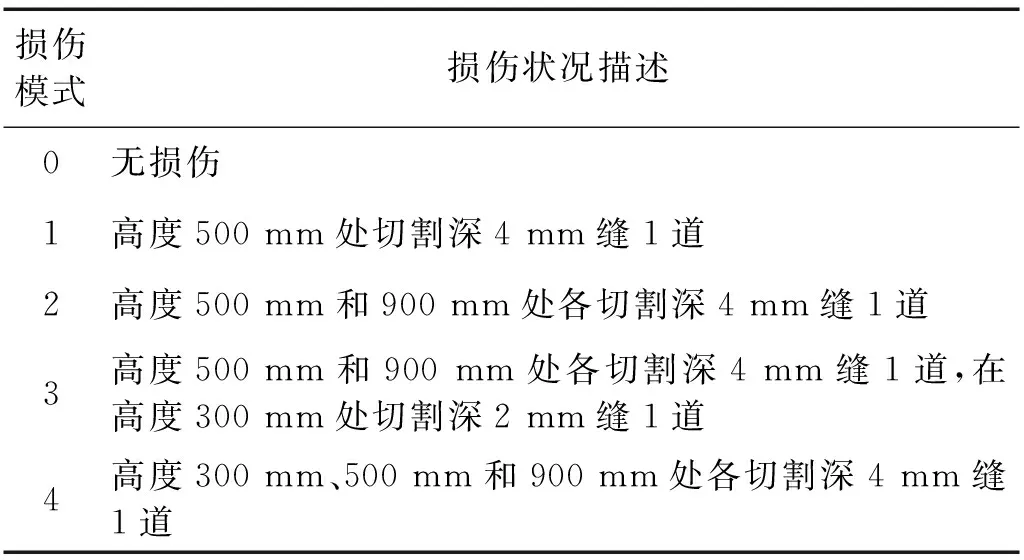
表11 振动台试验悬臂梁损伤模式Tab.11 Damage patterns of cantilever beam in shaking table test

图10 悬臂梁振动台试验装置图Fig.10 Device for shaking table test of cantilever beam
悬臂梁各个测点的加速度信号采样频率为5 000 Hz,每一种损伤模式下采集时长为30 s的加速度信号,即每个测点记录150 000个时刻点的数据,从而每种损伤模式可得到一个长度为150 000、维度为7的加速度信号序列。然后从每个序列中随机抽取1 000个长度为1 024、维度为7的子序列作为样本,共得到5×1 000=5 000个样本,按照8∶1∶1的比例划分成训练集、验证集以及测试集。
各个模型在训练集和验证集上的训练曲线,如图11所示。由图11可知:各个模型在经过一定次数的训练后均能达到较高的训练准确率,训练集和验证集的训练曲线基本一致,没有过拟合现象;CNN-MA收敛速度最快、稳定性好,CNN的收敛速度最慢但是较为稳定,CNN-LSTM和CNN-BiLSTM的稳定性较差,震荡比较严重。各个模型在训练集、验证集和测试集上的准确率,如表12所示。由表12可知:各个模型在本例的试验数据上均取得了较好的训练效果,准确率在90%以上;CNN-MA模型在训练集、验证集和测试集上都达到了100%,CNN-LSTM和CNN-BiLSTM在测试集上的识别准确率均在95%以上,CNN的识别准确率最低。
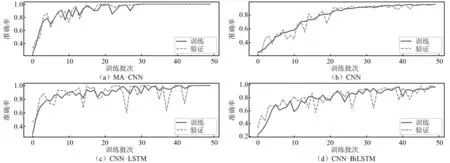
图11 各模型在悬臂梁振动台试验数据上的训练曲线FIg.11 Training curves of the models on shaking table test data of cantilever beam
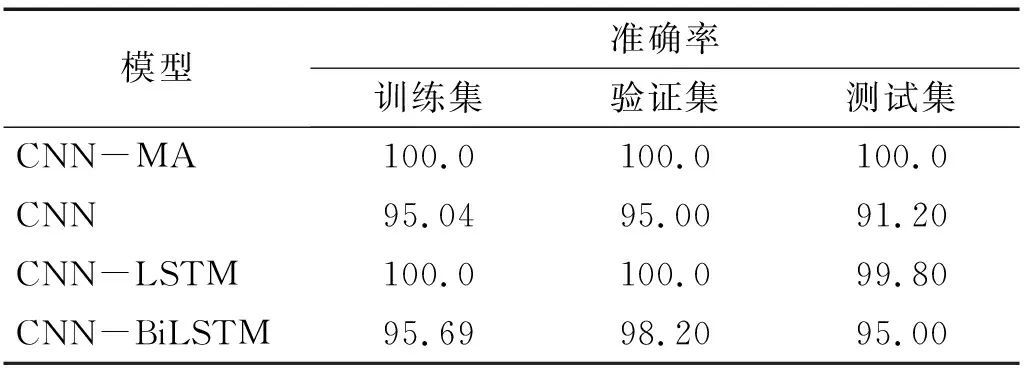
表12 各模型在悬臂梁振动台试验数据上的准确率Tab.12 Accuracy of the models on shaking table test data of cantilever beam 单位:%
训练好的各种模型在测试集上对各种损伤模式的识别精度,如表13所示。由表13可知:CNN-MA和CNN-LSTM模型对于各个损伤模式的识别均达到很高的精度,CNN和CNN-BiLSTM模型识别模式2和模式3时精度相对偏低。各种模型识别各种损伤模式的混淆矩阵,如图12所示。由图12可知:CNN-MA和CNN-LSTM能够不受干扰、非常准确地识别所有的损伤模式,可以准确捕捉到相近模式之间的差别,具有很好的损伤识别性能;其他模型在识别损伤模式2和模式3时会出现一定程度的相互干扰:CNN在识别模式2时,100个样本中90个识别正确,10个被误判成模式3,在识别模式3时69个识别正确,31个误判为模式2;CNN-BiLSTM识别模式2时,100个样本中87个样本识别正确,13个样本误判成模式3,识别模式3时88个识别正确,12个误判为模式2。
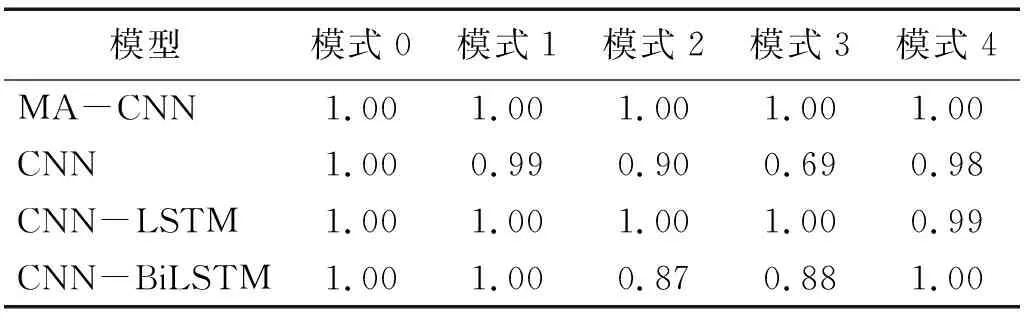
表13 各模型在振动台试验数据测试集上的损伤识别概率Tab.13 Damage identifying probability of the models on test data set from shaking table test
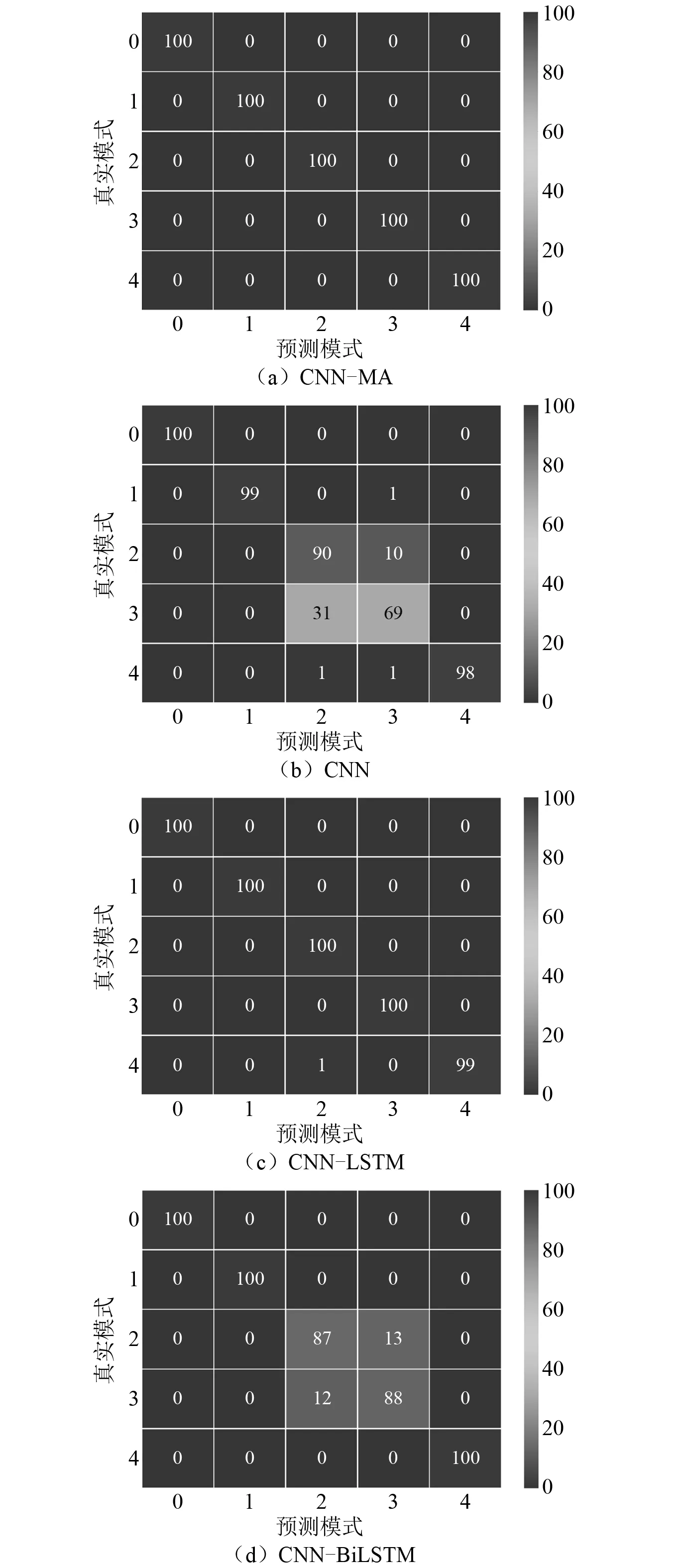
图12 振动台试验数据测试集上的损伤识别混淆矩阵Fig 12 Confusion matrix for damage identification on test data set from shaking table test
3 结 论
本文基于多头自注意力机制和CNN,以结构的振动加速度信号为输入,构建了一种结构损伤识别的CNN-MA模型,并通过网格搜索给出了模型结构和超参数取值的建议。模型通过CNN提取加速度信号中的局部特征,通过多头自注意力机制对信号中不同位置和不同表征空间中的重要信息进行关注,学习信号中的全局特征。在悬臂梁数值试验和振动台试验中,CNN-MA模型由于复杂度低,更加易于训练;由于能够实现对重要信息的关注、减少次要因素的干扰,与CNN,CNN-LSTM和CNN-BiLSTM等其他模型相比,CNN-MA模型具有更高的损伤识别精度和抗噪性以及更强的辨识能力和抗混淆能力。目前,本文仅对简单结构的损伤模式识别进行了研究,对于复杂工程结构的损伤识别以及损伤程度判别等问题需要做进一步研究。此外,CNN-MA模型与其他神经网络模型一样存在模型优化问题,本文仅对有限的网络结构和超参数组合进行了比选,需要进一步研究高效的模型结构和超参数的优选方法。
