基于平均场博弈的超密集5G小蜂窝网络下行功率管理

胡 先 童

(安徽工业大学 计算机科学与技术学院, 安徽 马鞍山 243000)

0 引 言

随着移动互联网和物联网的激增，加上移动智能设备的出现和移动应用的爆炸式增长，5G蜂窝网络被认为是极其密集的[1]。网络致密化被认为是5G最显著的特征之一[2]。在这样的超密集网络环境中，由于网络的规模，UEs数量巨大，功率控制和干扰感知，变得非常具有挑战性[3,4]。此外，网络中的时空流量需求波动、信道条件的动态性以及由于需要协调而增加的开销将进一步加剧用户数据网络中资源管理的挑战。例如，队列状态信息(QSI)的不确定性及其随时间的演变将在资源优化中发挥关键作用。

在5G时代，节点和设备数量巨大，从而导致了经典博弈的计算难度较大。这主要是由特定玩家的策略影响所有其他玩家的策略决定。由于大量设备的参与以及它们的控制参数彼此之间的严重耦合，用经典博弈论的方法不足以研究用户数据网络中的资源优化。如文献[5]设计了信道状态信息不确定的随机波束形成。然而，由于小蜂窝网络数量庞大，集中式干扰管理会遇到沉重的通信开销，并且随机部署和有限的回程容量，都会导致其可扩展性和灵活性变差。

MFG是一种特殊形式的微分博弈，适用于具有大量参与人的系统[6]。传统博弈论模拟了单个玩家与系统中所有其他玩家的互动，而MFG用所有玩家的集体行为的效果来模拟单个玩家的交互，系统中玩家的集体行为由平均场(Mean Field,MF)建模。平均场平衡(Mean field Equilibrium，MFE)是通过求解两个微分方程，即汉密尔顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman,HJB)和福克-普朗克-科尔莫戈罗夫(Fokker-Planck-Kolmogorov,FPK) 方程得到的。单个玩家与平均场的相互作用采用HJB方程来建模，根据玩家的动作，玩家的集体行为被FPK方程建模。MFG特别适合这种超密集的网络，因为玩家的数量可以趋向无穷，且MFG中的代理数量与性能无关。

在最近的大量研究中，MFG被用来解决基于UDN中的功率控制问题和边缘缓存问题。例如：文献[4]研究UDN中干扰问题，为了降低对完全信息的要求，考虑状态动态和成本函数的不确定性，建立了鲁棒功率控制平均场博弈。文献[7]提出了一种新的联合功率控制和用户调度方法，用于优化超密集小蜂窝网络的单位能量比特数的能量效率。文献[8]解决了密集天线接入网络中节能分布式功率和速度控制的问题。控制问题被公式化为一个微分对策，在这个对策中，无线接入网络的剩余电池能量和它们的位置被控制。文献[9]针对与传统宏蜂窝网络共存的密集小蜂窝网络，提出了一种新的分布式功率控制模式。将功率控制问题建模为随机博弈，证明了纳什均衡的存在性。文献[10]研究雾无线接入网的边缘缓存优化问题。考虑时变用户请求和雾接入点的超密集部署，提出了一种分布式边缘缓存方案，以共同最小化请求服务延迟和前端流量负载。文献[11]研究在大量小基站和用户情况下的蜂窝边缘缓存问题。提出了随机几何网络模型下的分布式缓存算法以及表征内容流行动态的时空用户需求模型。

在以上研究的基础上，研究一个拥有大量SBSs和UEs的UDN的下行通信系统，通过控制SBSs的功率提高 SBSs与其服务用户之间成功传输的概率，并考虑了SBSs的能量消耗问题。为了联合最小化数据成功传输速率成本和SBSs的能量消耗，建立了一个动态随机博弈来模拟该问题。DSG捕捉到SBSs之间的相互作用和SBSs状态的动态变化。由于求解的计算复杂度较高，该算法被近似为一个MFG，利用SBSs的超密集特性来解决这一具有挑战性的问题。在MFG中，所有SBSs的单个状态可以用一个统计MF分布来近似。通过求解耦合的HJB和FPK方程获得MFE。每个SBS能够基于其本地状态和平均场分布来确定动态最优功率控制策略。本方法在不需要与其他SBS进行额外信息交换的情况下，可以获得最优功率控制策略，减小了通信开销。同时能根据其最优功率控制策略，有效减小达到最小成功传输速率所消耗的成本。

1 系统模型

1.1 网络模型

考虑超密集5G小蜂窝网络的下行链路，由I个SBSs、K个用户和一个远程5G 基站(Base Station,BS)组成，如图1所示，其SBS被超密集地部署，并通过云端链路与BS连接。SBS集和UE集分别用J={1,2,…,i,…,I}和κ={1,2,…,k,…,K}表示。假设有I个SBS到用户设备的下行链路共享同一个信道。

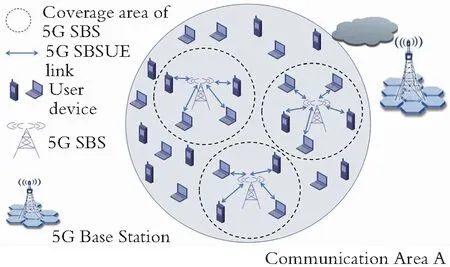
图1 UDN中的多个SBS

根据上述模型定义，SBSi与服务用户k在t时刻的数据传输速率为

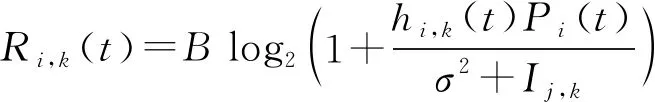
(1)

其中,B为传输带宽，Pi(t)为SBSi在t时间的传输功率,σ2为噪声功率。hi,k(t)表示SBSi和用户k在时间t时的信道增益。Ij,k=∑j≠i,j∈Nhj,k(t)Pj(t)表示其他SBSs造成的干扰。

当Ri,k(t)≥Rth时，下行通信可视为成功连接，其中Rth表示最小成功传输速率阈值。

(2)

hi,k(t)Pi(t)-R′(σ2+Ij,k)

(3)

1.2 队列状态模型和能量使用模型

假设SBSi发送qi,k(t)比特给UEk，第i个SBS队列的时间演化由下式给出[7]:

dqi(t)=ai(t)-Ri(t,Pi(t),h(t))dt

(4)

其中,ai(t)和Ri(·)是SBSi的到达和传输速率的向量，并且h(t)是信道增益的向量。

玩家i在t时刻的剩余能量状态Ei(t)等于可用能量的总量。同时，0≤Ei(t)≤Ei(0) ，其中Ei(0)是0时刻的能量。t时刻的功率控制应是任意Pi(t)∈[0,Pmax]，而Pmax为可能的最大发射功率。不失一般性，将电池剩余能量的演化律定义为[8，15]

dEi(t)=-Pi(t)dt

(5)

即电池能量Ei(t)随着发射功率Pi(t)消耗而减小。

根据介绍的系统模型，SBSi的整体状态可以用式(4)中的队列状态和式(5)中的能量状态表示为si=(qi(t),Ei(t))。

2 成本函数与动态随机博弈

2.1 成本函数

在t时刻SBSi的成本函数由如下两部分组成。第一个组成部分是与满足最小数据成功传输速率相关的成本Rth，用式(3)的平方来表示。考虑的成本函数的第二个组成部分是与SBS传输时消耗的能量。为简单起见，假设SBSs所消耗的功率与传输功率成正比。因此，成本函数可以表示为

Ji(t)=ω1(hi,k(t)Pi(t)-R′(σ2+Ij,k))2+ω2Pi(t)

(6)

ω1和ω2用来平衡成本函数的两个组成部分的单位。

2.2 动态随机博弈

每个SBS的控制策略随着动态方程式(4)和式(5)变化而变化。因此，最小化SBS式(6)的成本可以被建模为DSG。因此，将DSG定义为一个四维的{J，Si，Pi，Ji}。J指的是玩家的集合，它们是SBSs；其中Si和Pi分别是SBSi的状态和控制空间；Ji表示玩家i在有限时间范围内T的累积成本，表示为Ji=

在上述所建立的DSG中，玩家i的控制优化问题可以表述为

其中，s-i(t)={sj,j≠i,i∈J}表示其他I-1参与者的状态。

据动态规划理论，一个问题在整个时间区间[0,T]上的整体最优可以通过在时间反转的方式[12]中依次构造其子问题在时间区间[t,T]上的最优策略得到。相应地，可以将t时段内参与人i的值函数Ui(t,si(t))设为[t,T]时间段内的最小代价:

∂tsi(t)·Ui(t,si(t))]=0

在式(7)中定义哈密顿量:

H(si(t),Pi(t),Ui(t,si(t)))=

(7)

通过求解由于SBS之间的相互作用而耦合的I个 HJB，可以得到每个SBS的最优功率控制。然而，为了求解每个SBS的耦合HJB方程，需要每个SBS获取所有其他接入SBS的状态信息，这需要很高的计算复杂度，并且会导致巨大的额外通信开销。因此，可以通过引入平均场博弈近似来解决这个具有挑战性的问题。

3 平均场功率控制方案

3.1 平均场

由于耦合的偏微分方程而导致的原问题求解的困难性可以通过将原博弈近似为平均场游戏来解决，其中所有玩家的个体状态可以通过单个统计分布来捕获[14]。因此，可以显著减少耦合的PDE的数量，并且玩家能够以分布式方式做出决定。

平均场博弈的建立基于4个条件[15]:(1)参与者的理性;(2)玩家的连续性;(3)玩家状态之间的互换性;(4)平均场型参与者之间的互动。条件(1)是可以保证的，因为每个SBS都会做出逻辑决策。条件(2)是根据SBS的超密集部署来保证的。条件(3)成立，因为个体的影响在大量参与者中变得无穷小，而SBS指数之间的交换并不改变博弈的结果。条件(4)是确定的，因为每个SBS与MF相互作用，而不是游戏中的实际个体。

根据上述性质，原始的DSG可以近似为MFG，其中每个参与者在众多参与者中是无法区分的。因此，可以通过删除SBS指数来考虑一个通用玩家。在MFG中，一般参与者和其他参与者之间的相互作用充分地由其自身的状态和质量状态的统计分布特征。具体来说s=(qT,E)T∈X表示通用玩家的状态，m∈XT,XT=X×[0,T]表示平均场分布。m同时依赖于时间t和状态s(t)，可以表示为

其中，Ⅱ 表示指示器函数，如果给定条件为真，则返回1，否则返回0。注意，平均场分布是博弈中所有参与者状态的概率分布。

3.2 平均场近似(Mean Field Approximation，MFA)

(8)

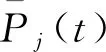
(9)

ω2Pi(t)

m(t,s(t)) 演化对应于FPK PDE为[10,11,17]:

-∂tm(t,s)=(m(t,s)·s(t))

(10)

其中，s是状态。

SBS MFG被定义为导出的HJB和FPK方程的组合，其中HJB方程重新定义为

∂tUi(t,si(t))+

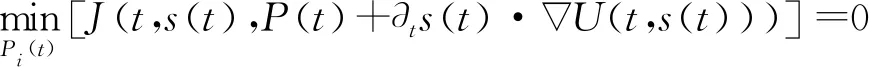
(11)

因此，SBS的MFG函数可以被定义为分别在式(10)和式(11)中给出的HJB和FPK方程的组合。HJB被称为倒向函数，这意味着它的最终值是已知的，需要确定U(t)在时间[0,T]的值。由于这个原因，HJB方程从t=T开始求解，在时间上向后，在t=0结束。FPK方程被称为前向方程，它随时间向前发展。HJB和FPK的互动演变导致了MFE。

4 平均场博弈解

4.1 平均场平衡

为了获得了MFE[9]，本文利用有限差分法。将时间间隔[0,T]，能量使用状态空间[0,Emax]，队列状态空间[0,qmax]离散为X×Y×Z空间。因此，将分别存在X+1、Y+1和Z+1个时间点、能量状态和队列状态。可以保证MF的正定性的Lax-Friedrichs方法[8，9]被用于离散方程。

4.2 FPK方程的解

首先通过使用Lax-Friedrichs方法求解FPK方程:

-∂tm(t,s)=Em(t,s)E(t)+qm(t,s)q(t)

通过使用Lax-Friedrichs方法，得到以下结果:

M(i,j,k-1)+M(i,j,k+1)]+

M(i,j-1,k)P(i,j-1,k)]+

M(i,j,k-1)P(i,j,k-1)Q(i,j,k-1)]

其中,M(i,j,k)、P(i,j,k)和Q(i,j,k)分别表示离散化网格中时刻i、能级j和队列状态k处的MF、功率和队列状态的值。

4.3 HJB方程的解

为了求解HJB方程，使用了有限差分技术。然而，由于哈密顿项的存在，该技术不能直接应用于求解HJB方程。因此，HJB方程被重新定义为以FPK方程为约束的相应的最优控制问题。引入拉格朗日乘子λ(t,s)得到拉格朗日函数。假设终端成本J(T)=0，LangrarianL(m(t,s),p(t,s),λ(t,s))也被离散化。

对于离散化网格中的任意点(i,j,k)，通过计算得到的Langrarian关于M(i,j,k)的一阶导数并使其等于零，可以重新排列以获得更新λ的以下等式:

λ(i,j-1,k)]+δtQ(i,j,k)

其中，

L(m(t,s),p(t,s),λ(t,s))=

λ(t,s)(∂tm(t,s)+E(m(t,s)E(t)+

随着FPK方程可以通过有限差分离散化并且解决，可以根据Karush-Kuhn-Tucker(KKT)条件获得最佳决策变量P*[18]。互动演变最终导致平均场平衡。

5 实验结果与分析

在本节中，提供了与所提出的平均场功率优化控制的超密集5G小蜂窝网络下行链路通信系统的仿真结果。为了简化模拟，假设有300个SBS和150个UE，并且SBS与其服务的UE是随机分布在500 m×500 m的通信区域A，如图2所示。不失一般性，假设信道带宽W=20 MHz，σ2=-70 dBm ,Ei(0)=25 J,Pmax=20 W,ω1=10,ω2=0.001。

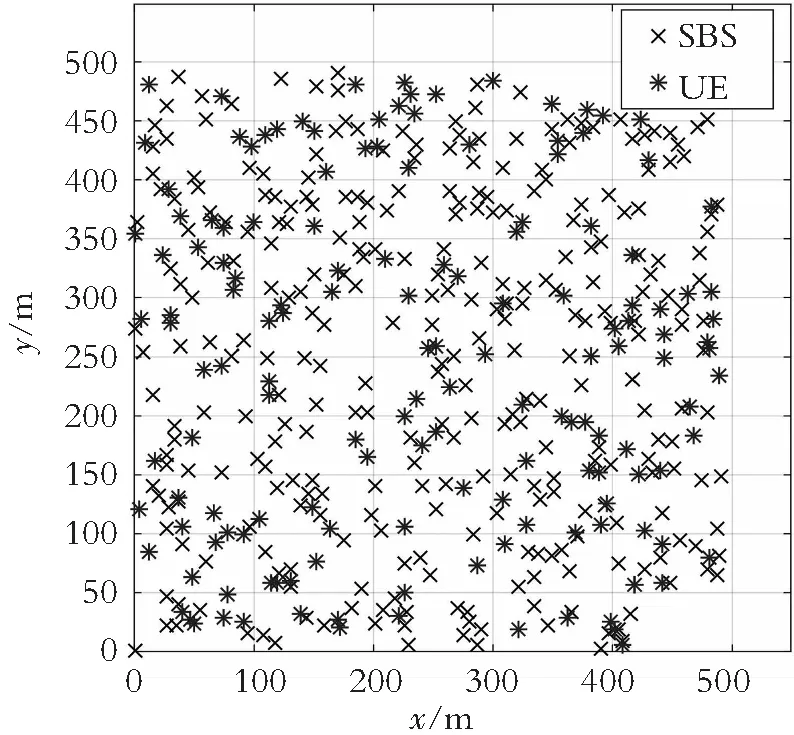
图2 SBS分布图

如图3所示，可以观察到与时间和SBS与匹配用户之间的队列状态有关的平均场的分布。因为初始的MF分布，设置为满足于高斯分布，所以初始平均场的分布主要在0.2到0.8之间。随时间的推进，可以观察到平均场趋向稳定趋势。

图3 MF分布图

如图4所示，可以观察到与时间和SBS与匹配用户之间的队列状态有关的数据率的分布。当把最小成功传输速率阈值设为Rth=0.3的时候，可以观察到数据率的分布会非常接近0.3这个阈值。这是因为，当达到最小成功传输阈值后，为了减小成本，数据率便不会再增加。

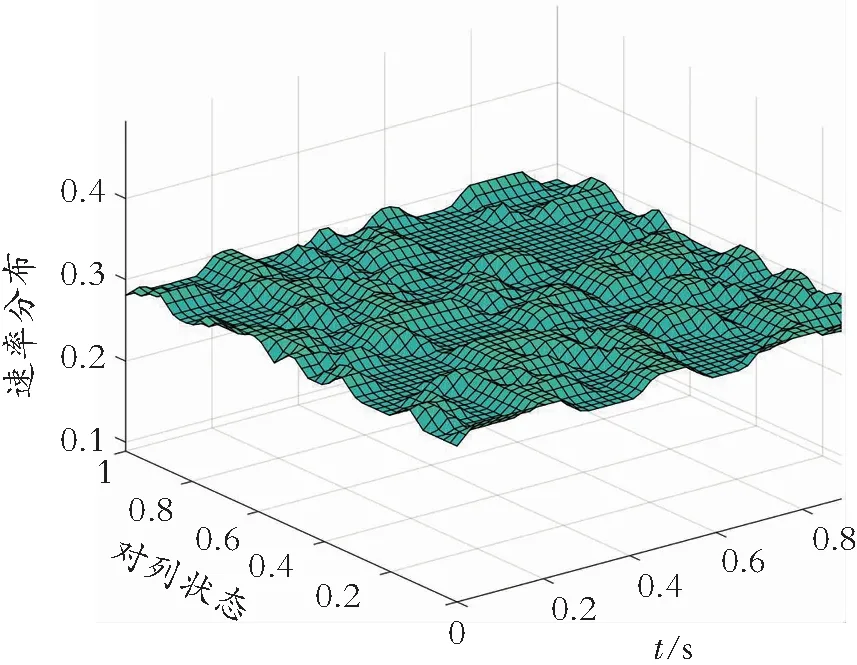
图4 速率分布图

在图5中，使用所提出算法的飞行能耗用蓝色圆曲线表示。而且，每个SBS都在初始时刻找到最优功率控制，导致了较高的成本。但在t=0.3后，该算法的成本降低，且低于均匀功率方式。此外，还给出了完全信息下的平均总成本，这可以称为理论性能，因为每个SBS都是基于局部信息知道其他SBS的信息的。图5中的红色方曲线显示了完全信息的平均总成本，这与所提出的算法类似。

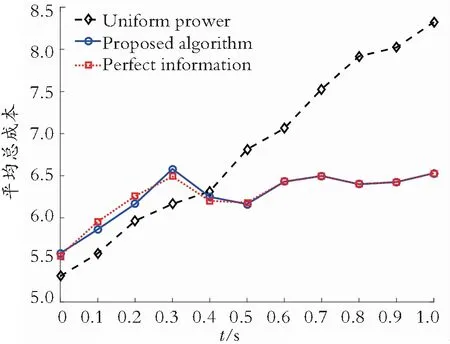
图5 N个SBSs的平均总成本随时间变化

6 结束语

本文研究了在UDN环境下小型基站的功率控制问题，并考虑了其能量消耗和队列状态信息。构造了一个队列状态和能源感知控制策略，称为MFG。基于导出的HJB和FPK耦合偏微分方程，并使用基于Lax-Friedreich和拉格朗日松弛方法的有限差分算法，得到了MFG的解。数值结果显示了SBSs的分布和行为。此外，通过与一些基准的比较，说明了所提出的最优功率控制方案的性能。该方案的一个优点是：在实践中可以分布式执行，以减轻中心管理人员的负担。