城市交叉路口智能控制与协同优化算法

张娟萍，韩 函

（1.山西工程科技职业大学，山西 晋中 030619；2.广西财经学院，广西 南宁 530100）

1 引言

经济的发展使得汽车保有量迅速激增，带来交叉路口的拥堵，使得现有交通道路的流量供给与迅速增加的需求之间产生矛盾，同时传统路口固定的信号控制方式也带来较多行车延误和油耗[1]，随着我国交通信息化技术的发展，根据路口交通实时情况建立车辆速度引导模型以及优化信号控制策略，以在有限的资源下确定确保车辆顺利通行，并减少延误和排放，对减少交通拥堵、缓解交通压力、节能环保以及提高现有道路资源的利用率具有十分重要的意义[2]。

目前已有研究大多基于车速引导优化控制，在不停车情况下通过路口，以达到降耗、减少污染的目的，为此，文献[3]针对网联车的行车时间需要，为减少其在交叉路口等候时间及减少停车与重启引起的额外油耗，设计了基于参数修正卷积的速度最优控制算法；文献[4]针对交叉路口的车道流向、功能平衡及信号相位冲突等复杂因素的相关性和饱和约束关系，建立优化控制模型，以关键流量比作为目标函数，减少模型参数并计算最优解，模型有效降低了车均延误并缓解了信号配时限制；文献[6]采用轨迹串联转向控制策略提高交叉口网联车通行效率，通过纵向分离和横向均衡建立上游车分布与转向信息库，以便于上游车轨迹导向，通过纵横向动力学模型，计算车辆位置演变时间，以精确控制行车轨迹；速度引导对于路口信号的时序较为充足时，引导作用较好，但对于拥堵严重导致配时不足时，连续的车速变化与启停反而加重油耗与时延，为此，车速轨迹引导与配时组合控制方法被展开研究，文献[6]以饱和度为约束，根据停车线后的交通状态实时状态构建延时模型，以优化路口信号参数设置，配合速度规划解决环形交叉口的左转通行问题；文献[7]分析传统信号配时在交通拥堵时的缺陷，以总油耗和总延误建立信号配时控制算法，针对双向冲突通过滚动时域对信号配时与行车轨迹同时进行协同优化；文献[8]将车队的换道行为引入控制模型中，建立轨迹与配时协同优化的混合整数控制模型，模型根据可换车道以及最小间隙判断换道行为；文献［9］建立基于非关键、跨相位和行人通行需求的相位分时优选模型，实现交叉路口相位与配时的同步优化，并顾及行人需求，提高了整体通行效率。

协同控制通过行车轨迹规划和信号相位配时优化有效提高城市交叉路口的通行整体效率，减少延时和污染排放，为此，在已有算法基础上，为实现车辆在城市交叉路口顺利通行的同时，减少行车延误，提出基于交叉口信号配时优化的车辆速度规划协同控制模型，模型将前车避碰引入到速度规划模型，并分不同情况计算车辆速度，然后针对传统信号配时局限，设计了信号配时优化模型，并与速度规划模型组成协同控制模型，通过信号配时优化，确保车辆通行的同时，减少行车平均延误。仿真实验验证了算法的有效性。

2 双目标协同优化模型

2.1 车辆基础模型建立

根据已有文献研究，在分析城市交叉路口通行状况时，车辆的动力学模型可以根据牛顿第二定律构建为［10］：

式中：Ae、Be、Ce－方程参数；u( )t－与车辆加速度相关的控制输入，x=[p，v，a]T－状态变量。这里采用式（4）所示的已有文献中的近似油耗方程作为后续算法性能分析的油耗模型，即

式中：fCruise、fAccel—车辆的巡航油耗和加减速油耗。

2.2 速度规划模型

设车队规模为Ni，所处车道为i，经过交叉路口，速度规划模型的目标函数可设置为：

在车队行进过程中，环境因素具有较为明显的不可控性，因此，在进行智能速度规划过程中，需要将车辆前车突然降速等情况引入到模型中，以避免碰撞。

设预测轨迹离散化后，当前车辆与前车的行车轨迹分别为

当前车的行驶速度比规划所需的最高限速要大时，此时只需根据规划加速度将车速调整为最大速度即可，而当前车速度低于规划的最高限速时，根据模型计算的加速度，可以将模型划分为来同的情况进行计算。

当Vtar≤Vm≤Vi时，车辆需要从当前速度调整到前车速度，得到车辆减速的距离时间和规划距离，即：

式中：L1—加速段结束位置；L2、L3—减速段开始和结束位置，其他两段车辆分别以最高速Vmax和前车速Vtar行驶。

当前车速度低于最大速度，且Vi≤Vm≤Vtar时，此时车辆直接加速会造成两车安全距离不足，需要以原速行驶一段距离后，再加速至前车速度，其速度规划为：

其中，在L1位置之前，车辆以原车速行驶，而在L2位置之后，与前车车速保持一致。

2.3 交通信号配时优化模型

在车辆建模基础上，需要根据车流与行人实时情况，建立信号配时基础模型，然后根据多个相位配时方案作为最优选择。相位基础模型的建立需要进一步考虑通行时间tMi的等式和不等式约束及信号相位的完整周期约束，即：

式中：m∈Ci，Ci—所有车辆集；sm(t0)、sm(th)—规划过程的起始和结束位置，可以由前文的车辆的运动模型计算，则车队总延误为各车延误累加。

2.4 基于优化配时的车速规划模型

基于交叉路口信号配时优化的车速规划模型，通过外部输入u使得式（14）所示目标函数达到最小值，即：

根据速度规划，当前车速通过加速或减速可以避开前车，并顺利通过交叉口时，车辆按速度规划模型进行速度规划，但如果以最大速度行驶，仍不能正常到达交叉口，需要路口通行开始时间较晚时，才能实现最优车速控制，此时，要对信号进行配时优化，此时的通行信号最早开始时间为：

3 实验分析及验证

为验证提出的基于交叉口信号配时优化的车速规划模型的有效性，以Matlab 2016a中搭建仿真场景，限速60km∕h，以式（4）所示模型分析实验过程中文中算法的油耗情况，实验所用的计算机环境为：CPU Intel（R）Core™i7 7820hq@2.9GHz，26G内存。

3.1 信号配时模型测试

车队在不同配时方式下通过交叉路口的延时情况，如图1所示。图中仿真过程的车流到达率分别为东西向3700veh∕h、南北向1500veh∕h，实验采用相同的速度规划模型[9]，并统计28个调整周期内所有车辆因信号配时不合理导致的延误，并计算多次实验的平均值，以消除随机误差影响。

图1 车辆平均延误Fig.1 Average Vehicle Delay

可以看出，这里配时优化模型整体上的平均延时时间要远小于传统固定配时的时间延误码，尤其在第10周期，文中算法的时间延误远小于传统方法，主要因为尽管通过速度调整较为有效的避免了车辆在交叉路口的停止与再启动。

但受传统固定信号配时限制，实验中在第10周期左右，车辆无法正常通行，从而造成额外延误，而文中算法通过合理配时，优化车辆行的起始和结束时间，从而使得车辆尽可能的通过交叉口，而避免产生额外延误。

3.2 协同优化控制模型性能测试

以交叉路口的某一个车道为研究对象，以传统速度规划模型和这里基于信号配时优化的协同控制模型对道路中的车辆进行实时车速调整，车辆的位置轨迹，如图2所示。图中实验结果为多次实验结果的平均值。

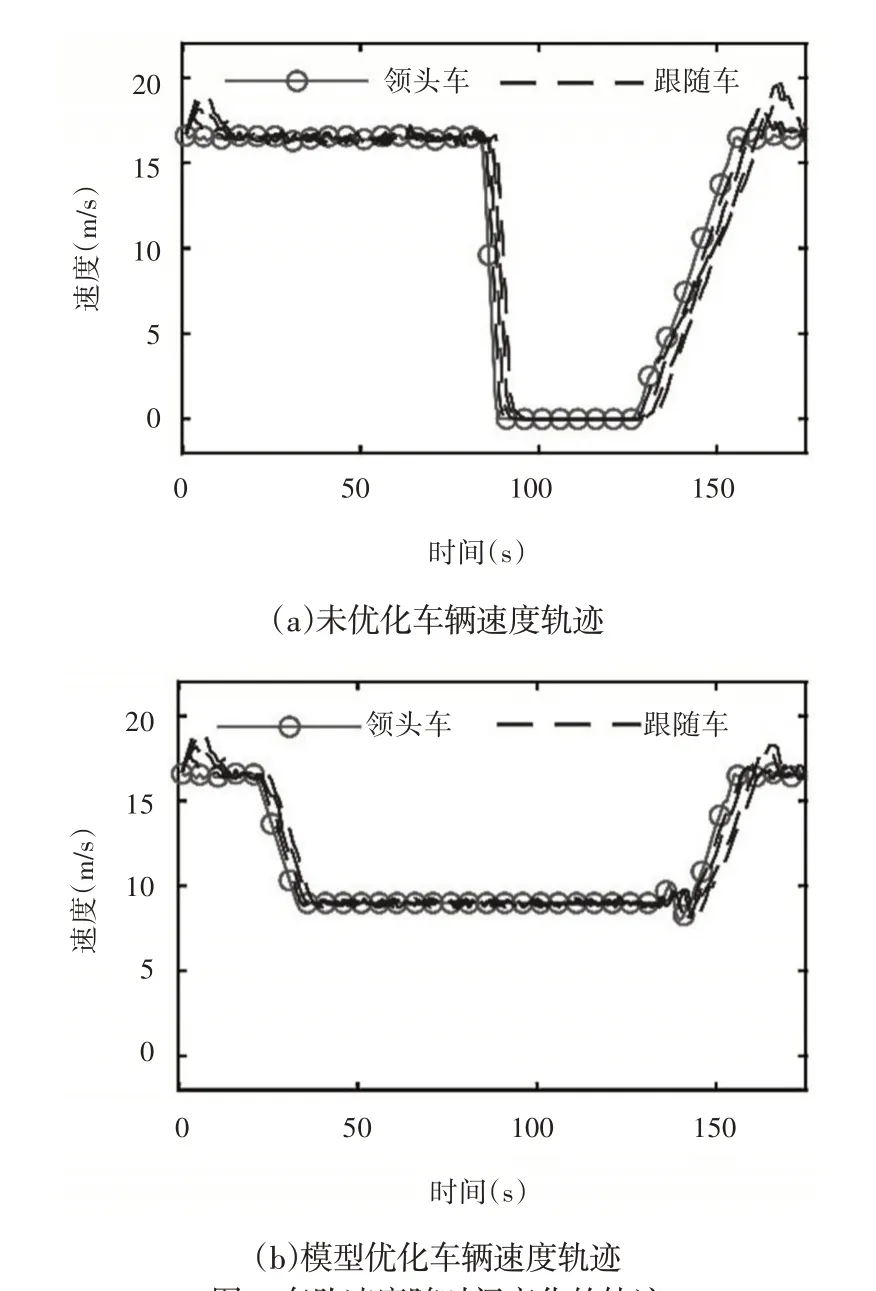
图2 车队速度随时间变化的轨迹Fig.2 Track of Fleet Speed Over Time

从图2（a）可以看出，在传统速度模型下，由于绿灯时间不合适且存在独行车阻挡，车队只能减速停止，然后再启动和加速通行。而如图2（b）所示，在改进速度模型下，在车队速度调整为9m∕s并匀速行进基础上，通过信号配时优化，在四个路口比较后，待车队到达停止线前，信号转为绿灯或适当延长绿灯时间，从而确保车辆完整通过交叉路口。

从总体实验结果可以得出，基于信号配时优化的速度规划模型，通过对交通信号配时的合理优化，在确保车辆顺利通过交叉路口的同时，通过配时优化，可进一步减少速度调整的幅度，从而减少车辆延误，从而验证了模型的有效性。

4 结论

为实现车辆在城市交叉路口顺利通行的同时，减少行车延误，提出基于交叉口信号配时优化的车辆速度规划协同控制模型，模型将前车避碰引入到速度规划模型，并分不同情况计算车辆速度，然后针对传统信号配时局限，设计了信号配时优化模型，并与速度规划模型组成协同控制模型，通过信号配时优化，确保车辆通行的同时，减少行车平均延误。仿真实验验证了算法的有效性。