仿人机械手运动空间范围特性分析

杨智勇，谢 迪，王 君，周红军

（1.湖北工业大学机械工程学院，湖北 武汉 430068；2.现代制造质量工程湖北省重点实验室，湖北 武汉 430068）

1 引言

近年来，机器人技术被广泛运用于建筑、医疗、商品分拣、汽车制造等行业，仿人机械手作为机器人的末端执行器，与人手具有类似活动关节，相比于执行特定任务所设计的传统机械手，具有更高的灵活性、通用性和适应性[1−2]。但由于仿人机械手结构相对紧凑，各运动关节较易出现运动干涉，约束了机械手运动空间范围。在机械手零部件结构尺寸一定的前提下，分析机械手指尖运动空间范围，对于机械手关键零部件结构尺寸及构型优化具有重要意义。

目前，针对仿人机械手运动空间范围特性分析已成为国内外研究热点。文献[3]型机器人手的基础上研制出了文献[4−5]灵巧手，其在外形上与人手极为接近，四指基关节都指向手掌内的一点；文献[6]四指机器人灵巧手的基础上设计了一种可沿锥面旋转的拇指结构，增大了拇指的工作空间尺寸，但未对其余四指进行扩大工作空间的设计[7−10]；文献[11]将手掌分为两部分，并通过齿轮连接，两部分分别安装拇指及其余四指，使得拇指可绕着手掌连接轴进行转动，但其余四指只能进行屈伸运动；文献[12]根据人手拇指运动特征设计了一种仿人机械手，拇指、食指和小指可绕着与手掌连接轴进行侧摆运动，但中指与无名指采用同一电机驱动，只能进行屈伸运动；文献[13−14]设计了一种仿人机械手，拇指不仅可进行屈伸或旋转运动，还能沿手掌上的导轨进行移动，但其余四指的近指节上由于集成了电机，导致近指节过长。综上所述，为保证机械手其运动关节尽可能与人手接近且增大仿人机械手运动空间尺寸，应为每根手指增加一个自由度，使得手指可以实现侧摆或旋转运动。

提出了一种仿人机械手新构型，其五指均能实现屈伸运动，拇指可绕其基关节的中心轴旋转运动，除中指外的其余三指均可实现侧摆运动；通过建立仿人机械手运动学模型，分析各手指运动学特性，求解手指指尖运动空间范围；分析机械手运动空间与手指侧摆摆杆长度、侧摆角度、旋转角度间的映射关系。

2 仿人机械手结构

仿人机械手实体图，如图1所示。该机械手包括手掌和五根结构尺寸相同的手指，依据人手手指分布特征，位于手掌内的手指为拇指，其余四根手指从左至右分别命名为食指、中指、无名指和小指；仿人机械手的各手指均由三个指节组成，即远指节、中指节和近指节，并通过基关节与手掌连接。中指由一个电机驱动，将电机的转矩和运动经由同步带传动机构传递给各指节，使各指节均向靠近手掌的方向运动，完成手指的屈伸运动；其余四指均由两个电机驱动，不仅可以完成屈伸运动，亦可完成侧摆或旋转运动。

图1 仿人机械手的五指结构Fig.1 Five−Finger Structure of Humanoid Robot

仿人机械手侧视图，如图2所示。手指侧摆电机将力和运动经由手指侧摆摆杆传递给基关节，使基关节沿着手掌上的槽口运动，完成手指的侧摆运动；拇指旋转电机将力和运动经由同步带传动机构传递给拇指基关节，使基关节绕其中心轴转动，完成拇指的旋转运动。手指侧摆角度、旋转角度直接影响着手指的工作空间大小，但由于手指各关节之间是耦合关联的，在计算其工作空间时较为复杂，因此可在其侧摆的平面上计算手指的工作空间。

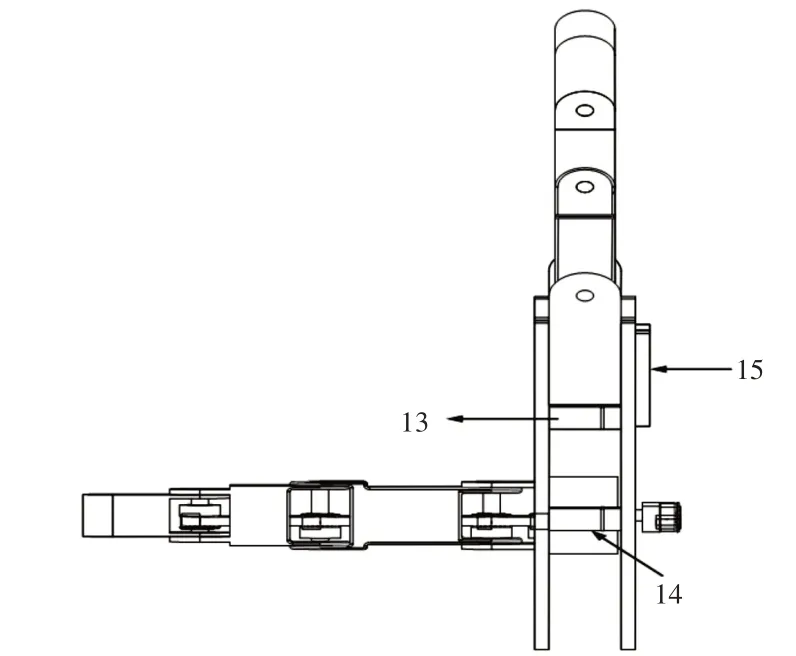
图2 仿人机械手侧视图Fig.2 Side View of Humanoid Robot

3 机械手运动学模型

由机器人机构学可知，机器人末端执行器可达点集合所包含的空间体积大小为机器人工作空间范围。将仿人机械手单根手指作为一个独立的机器人，其手指指尖即为机器人的末端，因此，分析仿人机械手的工作空间即为分析其五指指尖全部可达位置点。通过分析仿人机械手单指的运动学模型，求解单指手指指尖运动过程中全部可达位置点，并根据坐标系变换原则，分析仿人机械手五指运动学模型，求解仿人机械手五指指尖运动过程中的全部可达位置点。

3.1 单手指运动学模型

为描述手指指尖运动过程中全部可达位置点，在手指每根指节上固连一个连杆坐标系，分析手指的D−H参数，建立手指的运动学方程，求解手指指尖可达位置坐标点集合。依据对连杆附加坐标系的规定，Zi轴与关节轴重合，Xi轴沿着连杆的方向由i关节指向i+ 1关节，Yi轴由右手定则确定。以食指为例，食指关节坐标简图，如图3所示。

图3 食指关节坐标简图Fig.3 The Index Finger Joints’Coordinate Diagram

由图可知，在手指侧摆摆杆与手掌连接处建立手指的基坐标x0y0z0，z0轴沿着摆杆轴的方向，x0沿着摆杆指向手指的基关节。手指基关节处建立坐标系x1y1z1，近指节与中指节连接处建立坐标系x2y2z2，中指节与远指节连接处建立坐标系x3y3z3，手指指尖处建立坐标系x4y4z4。

手指的摆杆为连杆1，记为L1，近指节、中指节、远指节分别记为L2、L3、L4。食指的D−H参数，如表1所示。

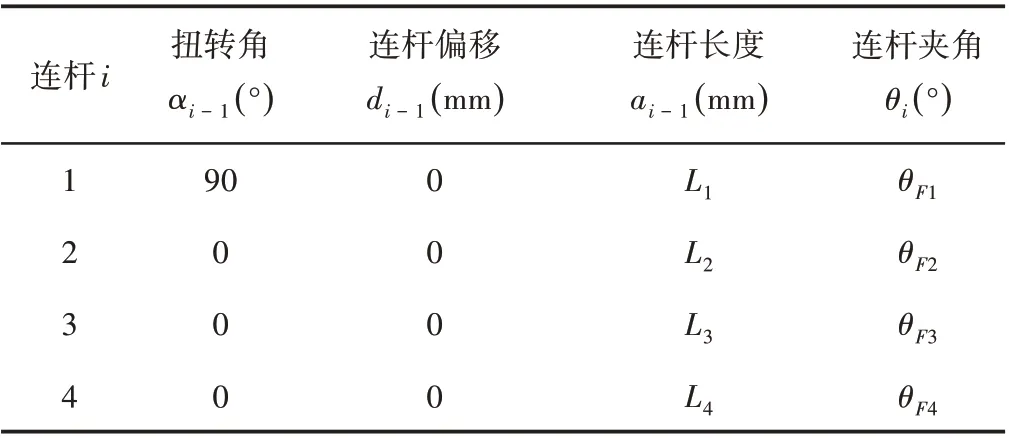
表1 食指D-H参数表Tab.1 The D-H Parameter Table of Index Finger

依据机器人坐标变换的链式法则，坐标系i−1到坐标系i的变换矩阵可写成［9］：

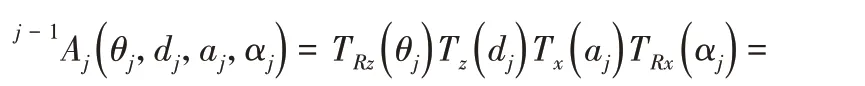
将机械手的各关节尺寸及其关节夹角代入到（3）中，求得机械手食指指尖坐标。参照食指各关节坐标系，机械手的中指、无名指、小指和拇指的D−H参数，如表2～表5所示。

表2 中指D-H参数Tab.2 The D-H Parameter Table of Middle Finger

表3 无名指D-H参数Tab.3 The D-H Parameter Table of Ring Finger

表4 小指D-H参数Tab.4 The D-H Parameter Table of Little Finger

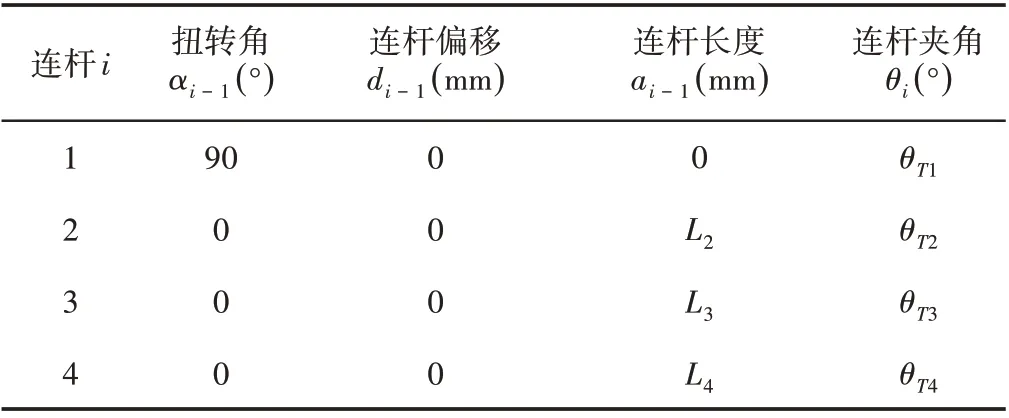
表5 拇指D-H参数Tab.5 The D-H Parameter Table of Thumb

3.2 五指运动学模型

仿人机械手的工作空间由五根手指运动范围确定，分析仿人机械手五根手指的运动范围，求解仿人机械手的工作空间尺寸大小。五指的基坐标系分别为CT0、CF0、CM0、CR0和CL0（其中，T表示拇指，F表示食指，M表示中指，R表示无名指，L表示小指），以中指的基坐标系CM0为全局基坐标系。

将不同手指的结构尺寸和各个关节角的转动角度分别代入式（4）、式（13）～式（16）中，通过计算可以得出运动过程中各个手指指尖在不同位置处的坐标值。

4 手指指尖运动范围分析

分析不同手指指尖位置坐标的表达式，在全局坐标系下手指的侧摆角度、摆杆长度、拇指旋转角度变化均会影响手指指尖坐标的x、y值，但不影响z值。故在全局坐标系的XOY平面对手指指尖位置点坐标集合进行分析，以食指为例，食指指尖可达位置点集合在XOY平面上的投影面积为S1，食指侧摆角度为θF1，食指在X轴方向的投影为LF=L1+L2cL2+L3cL23+L4cL234，其最大值记为LFmax， 则有：

通过仿真软件计算出食指在X轴方向投影的最大值为LFmax、拇指在X轴方向投影的最大值为LTmax，代入到式（17）和式（18），求出食指和拇指指尖可达位置点集合在XOY平面上的投影面积。

由式（17）可知，机械手手指指尖可达位置点集合在XOY平面上的投影面积与机械手侧摆机构的侧摆角度成正比关系。手指在进行屈伸运动时，其侧摆机构需保持静止以免影响手指的抓取性能。以食指为例，建立手指侧摆时的力学模型，其基关节与手指槽口连接处的受力情况，如图4所示。其中，G表示食指的重力，f表示基关节所受摩擦力，FN表示基关节对槽口的压力。

图4 基关节与槽口连接处受力示意图Fig.4 The Schematic Diagram of the Force Between the Finger Base Joint and the Notch

当手指基关节所受摩擦力最小时，为保持手指侧摆机构处于静止状态，侧摆机构与手掌间的摩擦系数记为μ，则有：

其中，θF1—食指侧摆的角度，由式（19）可得：

通过式（20），可确定机械手食指侧摆角度θF1的极限值。当机械手食指的侧摆角大于极限值时，食指侧摆到最大极限角度时侧摆关节与手掌间发生相对滑动，影响食指的屈伸运动。因此，手指侧摆角度大小应根据手指与手掌间的摩擦系数进行设计。

5 仿人机械手运动空间范围仿真分析

参考人手指尺寸和指关节的活动角度范围，保证机械手结构尺寸尽可能与人手接近，选定手指的各关节尺寸：L2=6cm、L3=4.2cm、L4=3cm，各手指的关节角为θM2=θM3=θM4∈[ 0°～90° ]、θF2=θF3=θF4∈[ 0°～90° ]、θR2=θR3=θR4∈[ 0°～90° ]、θL2=θL3=θL4∈[ 0°～90° ]、θT2∈[ 90°～180° ]、θT3=θT4∈[ 0°～90° ]。假定手掌采用3D打印材料制作，则机械手手掌的摩擦系数为0.36，根据式（20），给定手指的侧摆角度为θF1∈[ 0°～20° ]、θR1∈[ −20°～0° ]、θL1∈[ −20°～0° ]，手指旋转角度θT1∈[ −90°～90° ]，将其代入到式（7）、式（13）～式（16）式中，通过matlab里的Robotic toolbox工具箱中的LINK（）函数构建仿人机械手模型，以大拇指近指节关节夹角等于90°、其余四指的近指节关节夹角等于0°为手指的初始位置，仿真分析五指指尖位置坐标运动范围，以手指各个关节角为变量，在全局坐标系计算各手指指尖随关节角变化的所有位置点，仿人机械手指尖运动区间示意图，如图5所示。

图5 机械手指尖运动区间示意图Fig.5 The Motion Interregional Schematic Diagram of Robotic Fingertips

由图可知，中指指尖位置可达点的集合是一条曲线；食指、无名指、小指、拇指的指尖位置可达点集合均为曲面。在全局坐标系中仿人机械手手指的侧摆角度、摆杆长度的变化只影响手指指尖在x、y轴方向上的位置，不影响其在z轴方向上的位置，为研究仿人机械手工作空间范围与侧摆角度、摆杆长度间映射关系，分析在全局坐标系XOY平面内指尖位置坐标集合。手指指尖在XOY平面的投影，如图6所示。由图可知，由于中指未安装侧摆机构，其指尖位置点集合在XOY平面的投影是一条直线，相比之下，安装了侧摆机构的食指、无名指和小指，其指尖可达位置点集合在XOY平面上的投影形状为扇形，投影面积为51.6cm2；大拇指安装了旋转机构，其指尖可达位置点集合在XOY平面的投影形状为扇形，仿真计算可得面积为176.4cm2。

图6 手指指尖位置在平面XOY投影图Fig.6 The Projection of Fingertip Position on XOY Plane

为分析手指指尖可达位置点在XOY平面上投影面积与手指侧摆角度、侧摆摆杆长度间的映射关系，采用控制变量法，以食指为例，将摆杆长度视为变量，侧摆角度范围为定值，研究其投影面积与侧摆摆杆长度间的关系。通过仿真计算可知，当摆杆长度为2cm时，手指可达位置在XOY平面的投影区间面积为51.6cm2；当摆杆长度为4cm时，投影面积为51.6cm2；当摆杆长度为6cm时，投影面积为51.6cm2，不同摆杆长度下食指指尖位置在XOY平面的投影区间，如图7所示。由图可知，摆杆长度变化时，食指指尖可达位置点在XOY平面的投影形状也不同，但面积不变，故仿人机械手的工作空间尺寸大小与侧摆摆杆的尺寸无关。

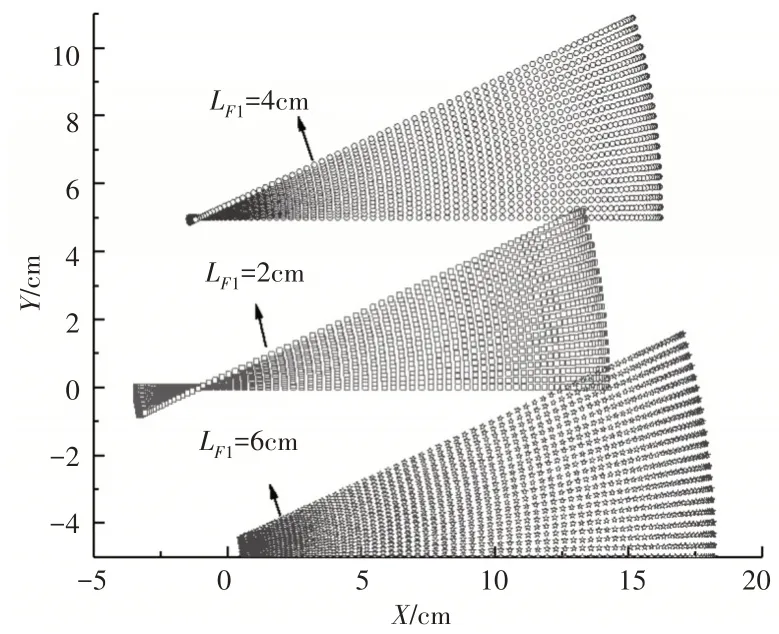
图7 食指指尖运动空间在XOY平面投影Fig.7 The Projection of Index Fingertip Movement Space on XOY Plane

同理，对食指、拇指采用控制变量法，分别将侧摆角度、旋转角度视为变量，分析指尖运动范围位置点集合在XOY平面上的投影区间，求解投影面积与侧摆角度、旋转角度间的映射关系。食指指尖空间位置点集合在XOY平面上投影面积与侧摆角度关系曲线，如图8所示。由图可知，食指指尖可达位置点集合在XOY平面上的投影面积与食指的侧摆角度成正比，故仿人机械手工作空间尺寸大小随侧摆角度的增大而增大。

图8 食指投影面积与侧摆角度关系曲线Fig.8 The Curve of Relationship Between Index Finger Projected Area and Side Swing Angle

拇指指尖运动范围位置点集合在XOY平面上的投影面积与手指旋转角度的关系曲线，如图9所示。由图可知，拇指指尖空间位置点的集合在XOY平面上的投影面积大小与手指旋转角度成正比关系，故仿人机械手工作空间尺寸大小随旋转角度范围的增大而增大。

图9 拇指投影面积与旋转角度关系曲线Fig.9 The Curve of Thumb Projection Area and Rotation Angle

但由于仿人机械手在抓取物体时需要拇指与其余四指的相互配合，才能完成抓取操作，因此，拇指旋转角度范围需根据其是否能与其余四指交互来确定，即拇指指尖位置可达点集合空间范围需与其余四指的指尖空间范围有重叠的部分。过度扩大拇指的旋转角度范围虽能增大拇指的工作空间，但部分工作空间范围无法对机械手抓取提供任何帮助，故拇指的旋转角度需根据四指侧摆角度来确定。

综上所述，仿人机械手工作空间尺寸与手指侧摆机构的摆杆长度无关，与手指的侧摆角度、旋转角度成正比。为了增大仿人机械手的工作空间，只需增大手指侧摆角度和旋转角度，手指侧摆运动角度范围需根据手指与手掌间的摩擦系数确定，手指旋转机构角度范围需根据拇指是否能够与其余四指之间有交互性进行确定。

6 结论

（1）设计了一种仿人机械手，其手指既可实现屈伸运动，也能完成侧摆或旋转运动。

（2）建立了单手指的运动学模型，通过对单指进行运动学分析，得出了指尖位置坐标与手指关节尺寸和手指关节角间的映射关系；并以中指基坐标系为全局坐标系，建立了在全局坐标系下的仿人机械手手指运动学模型和仿人机械手手指指尖数学模型。

（3）采用MATLAB 验证了仿人机械手工作空间尺寸大小与机械手指侧摆角度及旋转角度成正比，与侧摆机构的摆杆长度无关。通过仿真发现，当仿人机械手手指侧摆机构的摆杆长度较小时，仿人机械手的拇指与其余的工作空间均有重叠部分，表明拇指可与这四指进行交互运动，为后续进行仿人机械手的抓取规划提供理论依据。