融合改进鬣狗优化和Tsallis熵的图像分割
2022-12-30温秀平
张 军,温秀平,陈 巍
(南京工程学院 工业中心,江苏 南京 211167)
0 引 言
目前,图像分割方法[1]主要包括:边界分割法、区域分割法、聚类分割法和阈值分割法[2,3]。阈值分割法因为具有性能稳定、计算效率较高的优势,是目前最主流的图像分割方法。该方法的关键任务是基于图像像素点灰度级的比较,确定分割图像的最优阈值。阈值分割法又可分为单阈值分割和多阈值分割。单阈值分割仅通过一个阈值根据图像灰度直方图将图像分割为目标和背景区域。对于噪点较多的图像,该方法分割效果较差。多阈值分割则利用多个阈值将图像分割为若干类别,使各类别间的类间方差或熵值达到最优,分割效果明显优于单阈值分割法。
群体智能优化算法因为启发式的搜索原理可以大幅降低计算代价,已经广泛应用于求解图像分割的多阈值问题中。如:文献[4]结合了鲸鱼优化算法和飞蛾扑火算法的优势,求解了图像分割的多级阈值,但算法的依赖算法较多,计算复杂度较高。文献[5]提出了基于灰狼优化算法的多阈值图像分割算法,并结合Kapur熵和类间方差最优进行了实验对比,但受限于传统灰狼优化算法寻优精度的不足,最终的图像分割效率不高。文献[6]利用改进蜻蜓优化算法求解了彩色图像的最优分割阈值,利用差分进化机制提升了传统蜻蜓算法的求解精度,图像分割效果较为稳定。文献[7]设计了基于改进鲸鱼优化算法的多阈值图像分割模型,算法的全局搜索能力有所提升,适应度更高,阈值求解更加准确。文献[8]设计了基于蜘蛛优化算法的多阈值图像分割方法,在双模和多模阈值分割中有效提升了算法的计算效率和寻优精度。
以上基于不同群体智能优化算法的图像分割方法都具有一定效果,但智能算法本身的寻优过程主要由全局的粗粒度搜索到局部的精细开发过程组成。若算法的寻优效率和寻优精度没有得到根本改善,势必要影响图像分割阈值求解的准确性,甚至存在求解精度低或已得到局部最优的可能。
鬣狗优化算法SHO是目前最新的一种群智能优化算法[9],受启发于非洲地区斑点鬣狗种群的捕食行为。SHO算法因为稳定的寻优性能和高效的操作已经在工程优化[10]、特征选择[11]、资源系统调度[12]和MIMO-OFDM系统资源调度[13]等领域得到了广泛应用。不足的是,SHO算法的全局搜索和局部开采仅利用两个随机参数控制,导致在多峰值问题中易得到局部最优解、求解精度不足的劣势。
基于以上分析,本文将首先提出一种改进的鬣狗优化算法ISHO,然后结合Tsallis熵进行多阈值图像分割。通过利用混沌映射优化初始种群,使初始具备更多的多样性;对算法的收敛因子使用非线性的调节机制,从而均衡算法的全局搜索和局部开采过程;引入邻域重心对立学习机制计算个体的领域重心对立点,并择优保存,提高算法的全局寻优能力。以Tsallis熵为评估标准,利用ISHO算法求解分割最优阈值,并通过实验验证算法的有效性。
1 鬣狗优化算法SHO
鬣狗是一类强悍的中型猛兽,也是动物界有名的“机会主义者”,它们可以集体猎食瞪羚、斑马、角马等大中型食草动物。鬣狗优化算法SHO就是一种模拟了非洲斑点鬣狗种群捕食行为的新型群体智能优化算法。SHO算法对猎物的搜索过程由4步组成:包围猎物、狩猎、攻击猎物和搜索猎物。
(1)包围猎物
鬣狗种群具备判断猎物位置并对其实施包围的能力,其数学模型为
X(t+1)=Xp(t)-E·Dh
(1)
Dh=|F·Xp(t)-X(t)|
(2)
其中,Dh为猎物与鬣狗间的距离,t为当前迭代,F、E分别为摇摆系数和收敛系数,Xp(t)为迭代t时的猎物位置,X(t)为迭代t时鬣狗个体的位置。两个控制系数分别定义为
F=2·r1
(3)
E=2h·r2-h
(4)
h=5-t·5/Tmax
(5)
其中,r1、r2∈[0,1] 为均匀分布随机值,Tmax为最大迭代数,h为收敛因子,随迭代从5线性递减至0。
如图1所示为二维空间中鬣狗种群的捕食模型。鬣狗种群可以通过式(1)和式(2),首先判断并确定猎物(斑马)的位置信息,位置(A,B)上的鬣狗可以向着位置(A*,B*)的鬣狗的方向更新自己的位置以更加接近于猎物。同时,搜索过程中,通过调整两个控制系数F、E,可以使鬣狗遍布在猎物周围不同的位置,以形成包围之势。依此模型,还可以将其扩展至d维空间的搜索中。
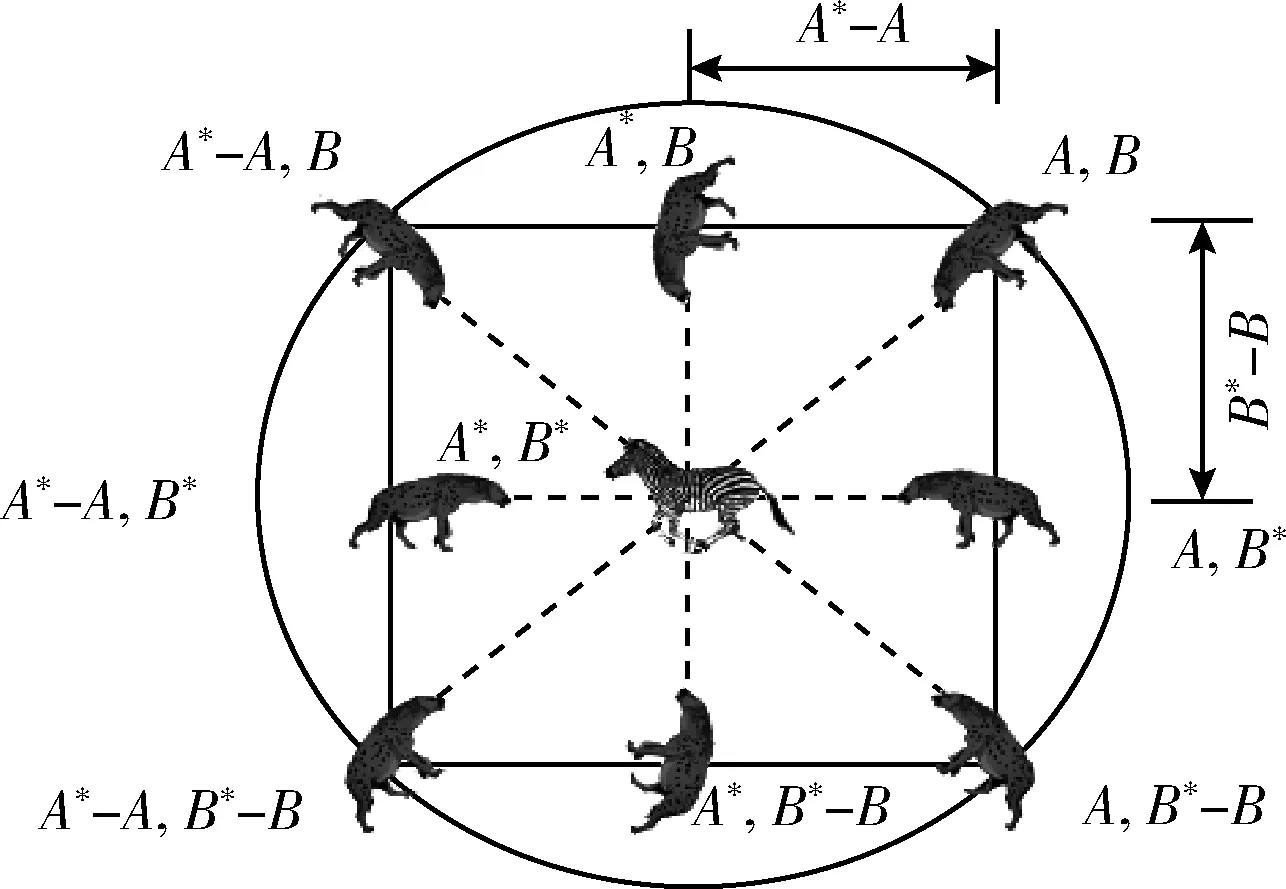
图1 二维空间中的鬣狗种群搜索过程
(2)狩猎
鬣狗可以通过建立可靠的种群网络,并结合猎物位置的判断进行分组猎杀,其数学模型为
Dh=|F·Xh-Xk|
(6)
Xk=Xh-E·Dh
(7)
Gh=Xk+Xk+1+…+Xk+N
(8)
其中,Xh为每一个最优鬣狗个体位置,Xk为其它搜索个体的位置,N为群组中的鬣狗数量,定义为
N=countnos(Xh,Xh+1,Xh+2,…,(Xh+σ))
(9)
式中:σ为[0.5,1]间的随机值,添加σ后,nos为可行解数量并计算所有侯选解,其与给定搜索区域的最优解相似,Gh为N个最优解组成的群组。
(3)攻击猎物
该过程相当于SHO算法的局部开发过程,该过程通过收敛因子h的递减实现。当h减小时,收敛系数E随之减小。而 |E|<1时,鬣狗即会对猎物进行攻击。其位置数学模型为
(10)
式中:X(t+1) 用于保存最优解,同时,其它个体的位置将根据该最优解进行动态更新。
(4)搜索猎物
该过程相当于SHO算法的全局搜索过程。一般情况下,鬣狗将根据Gh中保存的最优解群组的位置来搜索目标猎物。但当 |E|>1时,鬣狗就会随机分散,并远离当前猎物,从远离猎物的方向对其它区域进行搜索,以此避免生成局部最优解。
(5)SHO算法过程
输入:鬣狗种群Xi,i=1,2,…,n
输出:最优个体位置
(1) 参数初始化,包括:h、F、E、N、Tmax,并初始化种群
(2) 计算种群中每个鬣狗个体的适应度
(3) 记录当前最优个体Xh
(4) 根据式(8)、式(9),构建最优个体组成的群组Gh
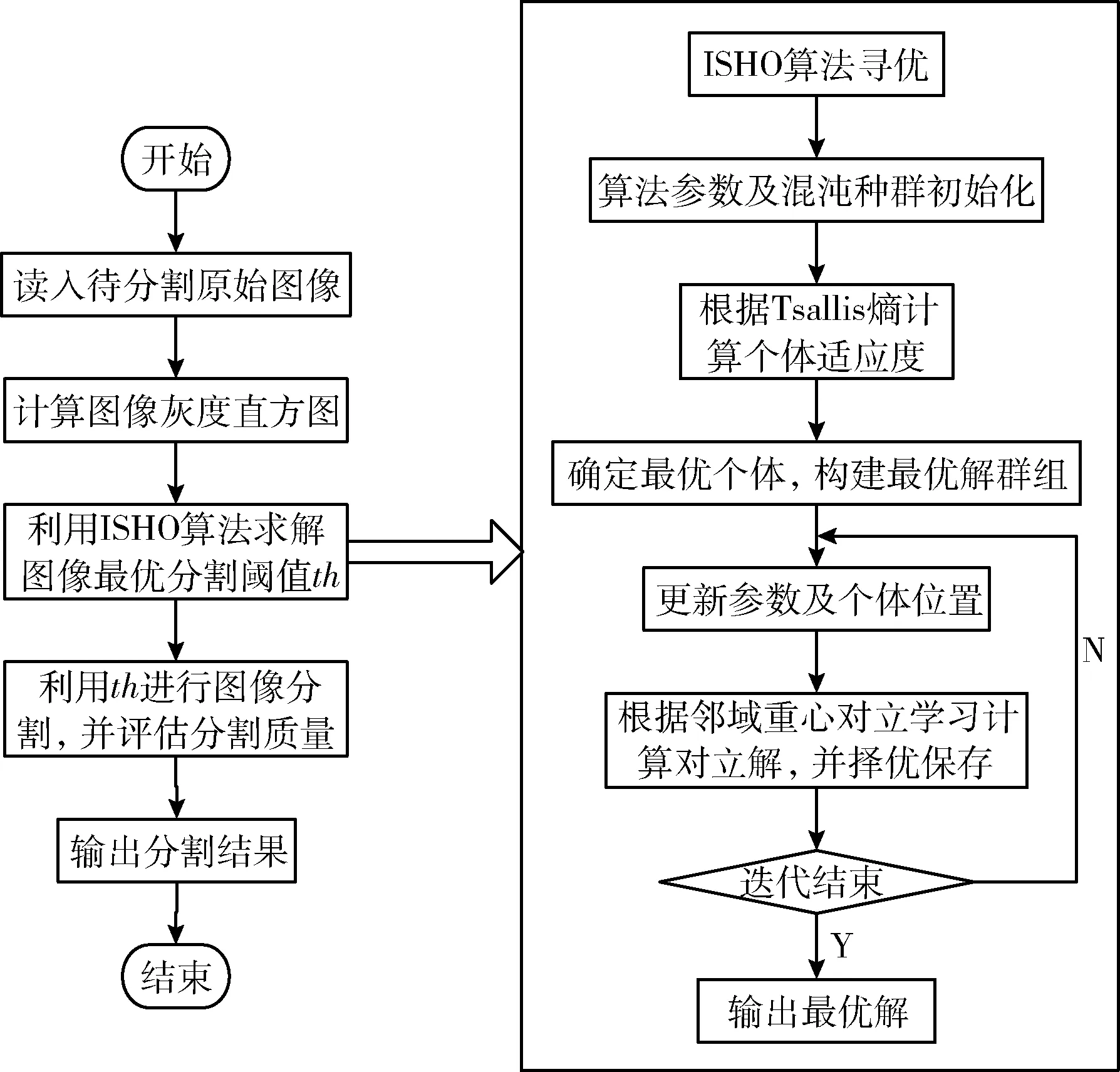
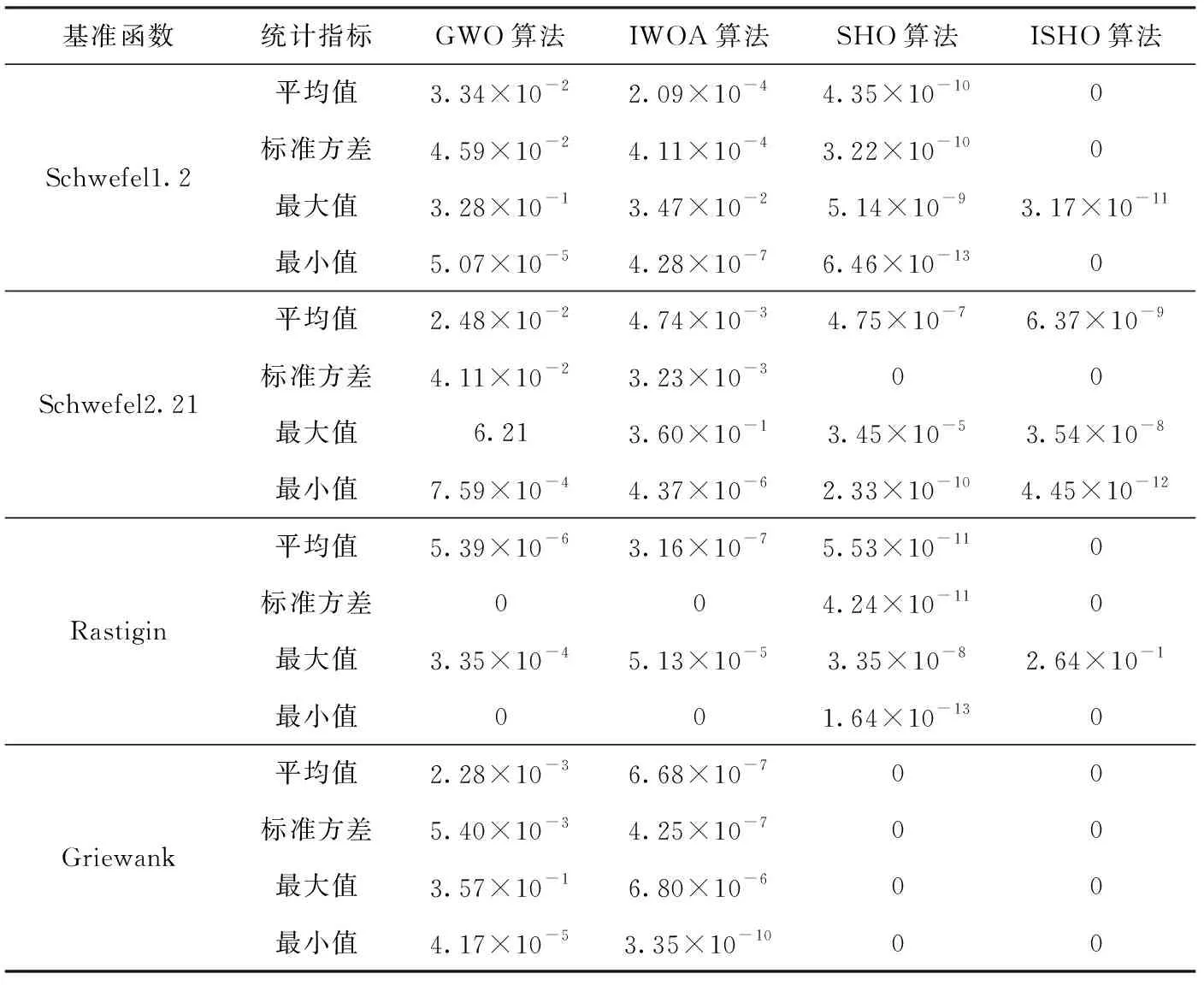
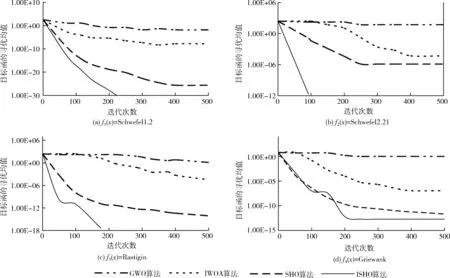
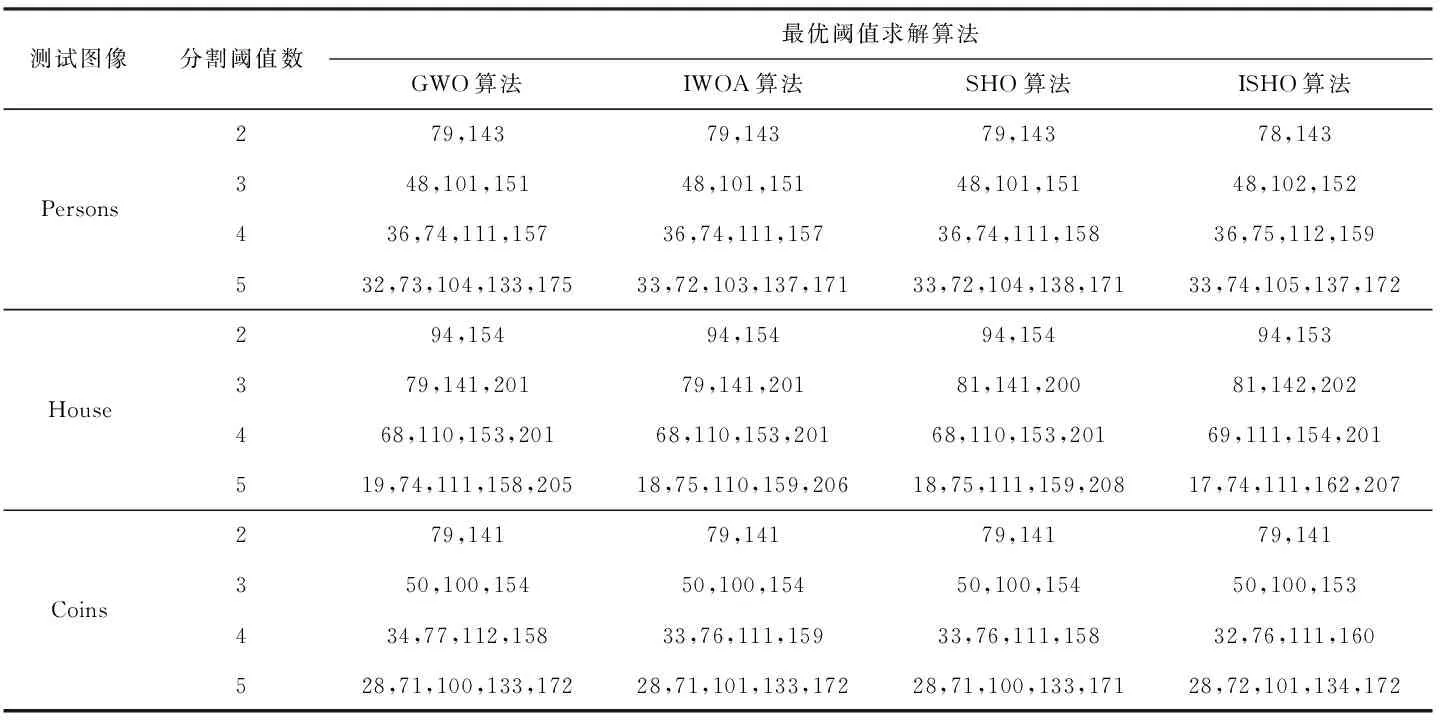
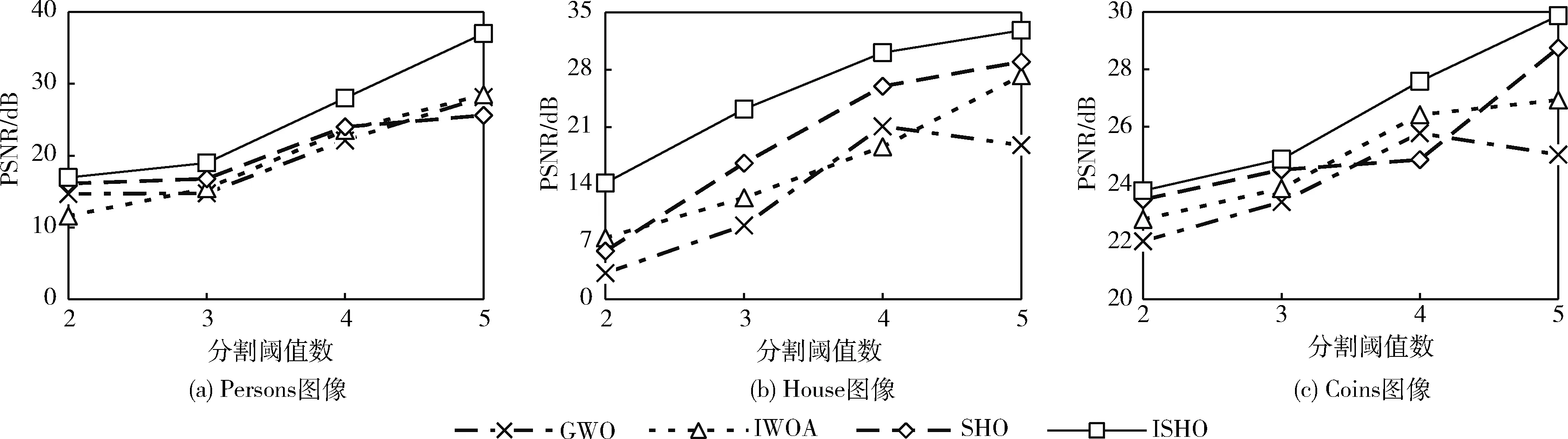
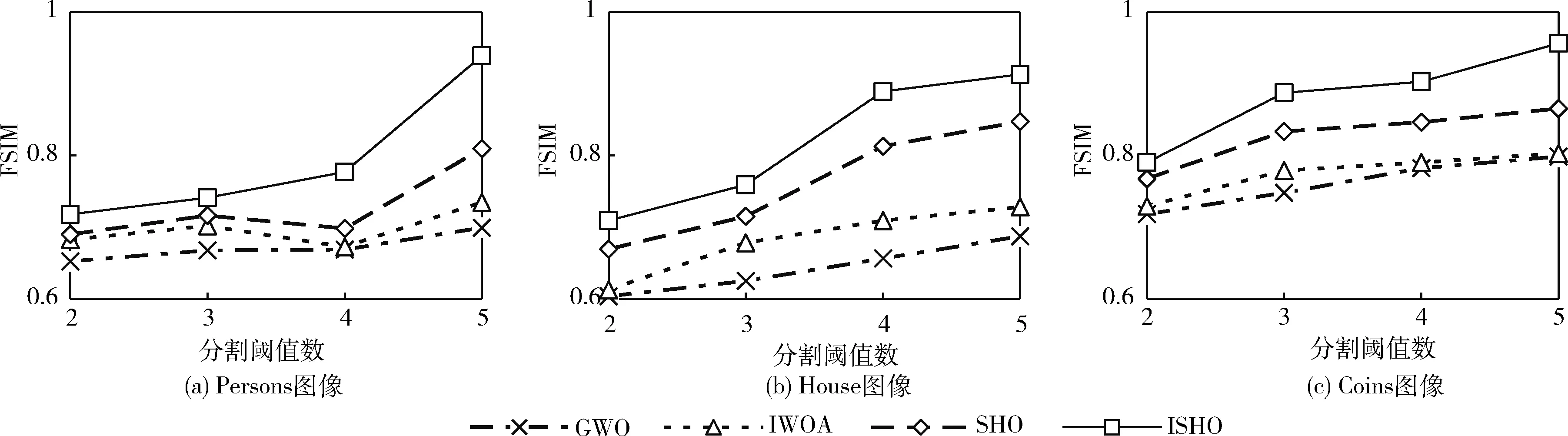
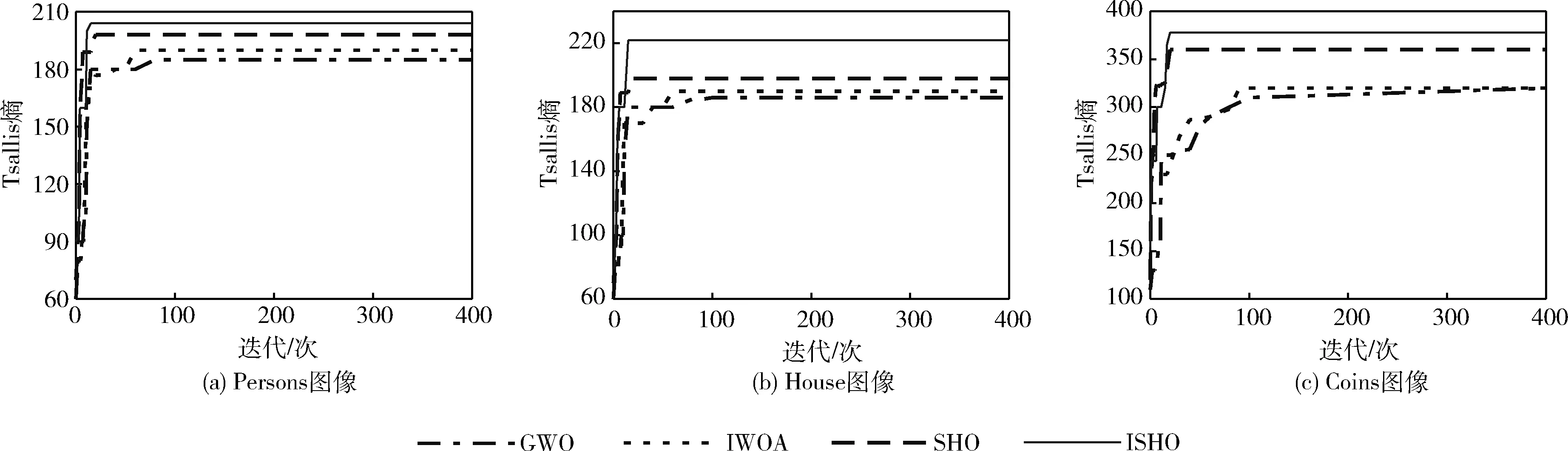
(5) whilet (6) for 每个个体 do (7) 根据式(10)更新个体位置 (8) end for (9) 更新参数h、F、E、N (10) 越界检查 (11) 重新计算个体适应度 (12) 若有更优个体, 则更新Xh (13) 根据Xh更新群组Gh (14)t=t+1 (15) end while (16) 返回Xh 群体智能优化算法具有初值敏感特征,初始种群分布的合理性对算法寻优精度和收敛速度都具有重要影响。如果初始种群邻近最优解所在区域,算法寻优精度会更高,收敛速度也更快;反之亦然。传统的鬣狗优化算法以Rand函数产生随机数的方式随机初始化种群部署,缺乏多样性。混沌系统是非线性环境中的一种普遍现象,看似混乱,实则综合具有规律性、遍历性和随机性,可以不重复遍历到所有状态。通过混沌映射规则将混沌变量映射至混沌空间,在混沌空间内搜索后,再将结果映射回原始问题解空间中,可以克服随机化分布的遍历不足、种群多样性缺失等问题。 目前,Logistic混沌映射比较常见,但根据其分布曲线图可知,其混沌值在边界两端([0,0.1]和[0.9,1]两个区域)取值率过高,遍历过程均匀性缺乏,会降低算法收敛速度。Tent混沌映射证明比Logistic遍历性更好,能够在[0,1]区间生成分布更均匀的初值,且不缺乏遍历性。因此,ISHO算法结合Tent混沌映射生成初始的鬣狗种群位置。Tent映射表达式为 (11) 式中:u为混沌参数,y(t)是迭代t时的Tent混沌值。u=1/2是混沌Tent映射的典型形式,此时生成的混沌序列分布均匀,对不同初值参数可以生成近似一致的分布密度。 确定混沌序列后,通过下式将混沌序列映射为个体位置 X(t)=UL+y(t)×(UB-UL) (12) 式中: [UL,UB] 为个体搜索的区间,对应种群搜索范围。由于混沌序列的生成值取决于初始值,初始值发生微小变化也会带来混沌值的巨大变化,此时生成的初始种群将兼具随机、遍历等特征,多样性更好。 根据SHO算法的包围猎物机制,收敛系数E控制着鬣狗的搜索方向。当 |E|>1时,鬣狗将从远离猎物的方向进行搜索;当 |E|<1时,鬣狗将对确定的目标进行攻击。前者对应于全局搜索过程,后者则对应于局部开采过程。E的变化则由收敛因子h控制。根据h的计算公式(5)可知,其值将随着迭代线性地从5递减至0。对于SHO算法,迭代初期,h值较大可以增大搜索步长,拓展搜索空间,避免寻优过程过快收敛;迭代后期,h值较小可以减小搜索步长,提高算法的局部精细开采能力,加快算法收敛。 然而,全局搜索与局部开采之间并非完全线性切换,尤其在多峰值情形的寻优过程中,极容易出现局部最优解。为此,ISHO算法将基于正切函数引入一种非线性的收敛因子调整方法,具体公式如下 (13) 式中:hinitial、hfinal分别为h的初值和终值,Tmax为最大迭代数,μ为收敛因子的衰减因子,μ>0。根据式(13)可知,h将随迭代次数呈非线性递减,相应E值也将呈非线性递减。迭代初期,h取值较大,但递减缓慢,可以更大步长实现更充分的全局搜索。迭代晚期,h值变小,但递减加快,此时可以较小步长更快的靠近最优解,加速算法收敛。这种以不同速率递减的收敛因子调整策略更加符合鬣狗的搜索行为,将有助于算法的局部开发与全局搜索的协调进行,也可以确保鬣狗种群更高的狩猎成功率。 此外,正切函数只是收敛因子非线性调整的一种方式,指数函数、正余弦函数均可以实现对收敛因子的非线性调整,由于不同函数在曲线上表现出的衰减都有所不同,因此,这就决定了全局搜索与局部开采之间切换时机的不同,选择正切函数是本文改进算法的一种思路,其它几种非线性切换函数能否得到更好的分割效果需要在后续实验中通过对比分析才可以确定。 对立学习OBL可以通过评估当前解及其对立解的方式,以择优形式加速群体智能优化方法的寻优过程。但传统的对立学习机制在计算对立点时仅利用了维度空间的边界值,忽略了群体整体寻优的搜索经验。而重心对立学习则是以群组重心为参考点计算对立点,融合了群体的搜索经验[14]。相关定义如下: 定义1 重心。令 (X1,X2,…,Xn) 为d维空间中的n个点,则其重心为 (14) 则 (15) 定义2 重心对立点。令M为一个群组的重心,则群组中的某位置点Xi的对立点为 X′i=2×M-Xi,i=1,2,…,n (16) 由于对立点位于动态边界的搜索区间,可将其记为Xi,j∈[aj,bj]。 而动态边界可以不断缩小搜索区间,即 aj=min(Xi,j),bj=max(Xi,j) (17) 若对立点超出搜索边界值,则按以下方式重新计算重心对立点 (18) 重心对立点虽然可以借助群体搜索经验,依靠群体重心的方式计算对立点,但由于所考虑的重心仅有一个,导致对立解缺乏多样性。为此,改进算法ISHO进一步将利用邻域重心对立学习的方式计算对立点。令Xi为种群n中的个体i,Mi为个体i所在邻域的重心,则邻域重心对立点定义为 X′i=2×k×Mi-Xi,i=1,2,…,mi (19) 式中:mi为鬣狗i所有邻域中的个体数量,k∈[0,1] 为均匀分布随机数。 ISHO算法在计算邻域重心对立点时,采用的是利用随机拓扑结构进行邻域划分,即:为鬣狗个体随机性地选择其邻居个体。若种群最优解未发生更新,则需要重新选择其邻居。此外,当随机拓扑结构造成邻域个体仅包含自身、或除自身外的另一个鬣狗个体时,若仍按原始重心对立点的计算公式,会出现对立点与自身重合的情况,同时造成重复评估,影响寻优收敛速度。而引入随机值k后,可以避免出现对立点重复,拓展对立点范围,避免个体重合带来的重复评估。 图2是ISHO算法的流程。 图2 ISHO算法流程 ISHO算法的时间复杂度。令鬣狗种群规模为n,搜索空间的位置维度为d。种群初始化过程需要根据搜索个体的数量、搜索位置上下界生成初始种群的初始位置,其时间复杂度为O(n×d)。 接下来,计算种群适应度的时间复杂度为O(n×d×Tmax),Tmax为ISHO算法的最大迭代次数。定义鬣狗群组的时间复杂度为O(N×Tmax),N为组成群组的最优解数量。邻域重心对立学习机制需要遍历n个个体的所有维度位置,且需迭代进行,故该过程的时间复杂度为O(n×d×Tmax)。 综上,ISHO算法的时间复杂度为O(N×n×d×Tmax)。 与标准SHO算法的时间复杂度保持一致,说明改进算法并未增加计算代价。 令图像I拥有L个灰度级,nt个阈值构成的集合th={th1,th2,…,thnt},th将图像I分割为K个类别 {C1,C2,…,CK},nt=1,2,…,K-1, 且th1 Tsallis熵是香农熵的扩展形式,也称非广延熵[15]。该熵值考虑了图像中的非叠加信息,可以实现在噪声图像中的健壮图像分割。在单阈值情形下,阈值th将图像分割为目标区域和背景区域。则Tsallis熵的目标函数为最大化图像类别的信息量,可表示为 f(th)=max[Sq,1(th)+Sq,2(th)+(1-q)Sq,1(th)Sq,2(th)] (20) 式中:q为熵系数,用于衡量熵值的非广延度,Sq,1、Sq,2分别表示目标区域和背景区域的熵值,计算为 (21) 式中:w1(th)、w2(th) 为两个类别的累积分布函数,定义为 (22) 式中:Phi为灰度级i的概率分布。若令H为图像的灰度直方图,NP为图像像素数,Hi为图像灰度级i包含的像素数,则 (23) 对于多阈值图像分割问题,阈值集合为th,则Tsallis熵目标函数为 f(th)=max[Sq,1(th)+Sq,2(th)+…+Sq,K(th)+ (1-q)Sq,1(th)Sq,2(th)…Sq,K(th)] (24) 其中 (25) 各类别的累积分布函数为 (26) ISHO算法以Tsallis熵目标函数(24)作为评估鬣狗个体位置优劣的适应度函数,以迭代寻优的方式求解图像分割的最优阈值。算法的搜索空间为图像的灰度级空间,即灰度级L。若分割阈值为th={th1,th2,…,thn t}, 则阈值thi满足0 且为整数。以Tsallis熵最大为目标评估鬣狗个体的适应度,通过若干次的迭代寻优,求解满足式(24)最大的分割阈值解向量th。基于改进鬣狗优化算法的Tsallis熵多阈值图像分割的过程如图3所示。 图3 图像分割流程 实验验证分两部分进行,第一部分验证ISHO的标准函数上的寻优性能,第二部分以ISHO算法求解Tsallis熵最优的图像分割阈值,再做图像分割。实验平台都在MATLAB 2019a下进行,系统环境为Windows 7操作系统,CPU为Intel Pentium 3.2 G,内存为8 G。实验部分先利用表1的基准函数测试验证ISHO算法的寻优性能,4个基准函数即为需要寻优最优解的目标函数,搜索空间为寻优时个体的寻优范围,fmin为函数理论可达的最优值。前两个基准函数是单峰函数,仅存在一个全局最优值,比较容易搜索;后两个基准函数是多峰函数,存在多个深入内部的极值点,且有一定振荡特征,较单峰函数搜索空间更为复杂,易于陷入局部最优处。 表1 基准函数 再选择伯克利图像库中3幅图像Persons、House、Coins进行图像分割实验(可扩展至其它图像上实验)。如图4所示,Persons图像为室内人物图,且室内背景较为复杂,物品摆设、家具繁多,House图像为近景建筑图,房屋墙面形状及与背景树林的分割是难点,Coins图像为近景相似物图,其硬币表现的纹理分割是其重点。不同类型的图像有助于测试改进算法ISHO的全面分割性能。 图4 测试图像样本 算法参数中,最大迭代数Tmax=400,种群规模n=30,个体搜索空间[UL,UB]为[0,255](对应图像的灰度级范围),混沌参数u=1/2, 收敛因子h的初值hinitial=5,终值hfinal=0,收敛因子的衰减因子μ=2。同时,图像分割阈值数nt分别选取K=2、3、4、5进行计算。选择引言部分提到的改进鲸鱼优化算法IWOA[7]、灰狼优化GWO[5]以及标准鬣狗优化算法SHO[9]进行实验对比分析。对于IWOA算法,收敛因子从2递减至0。对于GWO算法,收敛因子同样从2递减至0。SHO算法的参数与ISHO算法设置基本相同。 为验证算法性能,需要对图像分割质量进行评估。选择峰值信噪比PSNR、特征相似度FSIM进行定量分析。其中 (27) (28) 其中,I(i,j) 表示原始图像,I′(i,j) 为分割图像,ε、ξ分别对应图像像素的行、列数。该指标根据图像分割前后的像素点间的均方差比较图像相似性。可以评估图像失真,值越大,图像失真越小 (29) 式中:Ω为整体图像像素域,SL(x) 为相似度分值,PCm(x) 为相位一致性度量,定义为 PCm(x)=max{PC1(x),PC2(x)} (30) 式中:PC1(x) 和PC2(x) 分别为两个区域的相位一致性,分别为 SL(x)=[SPC(x)]α·[SG(x)]β (31) (32) (33) 其中,SPC(x) 为相位一致性的相似度量,SG(x) 为两个区域G1(x) 和G2(x) 的梯度级,α、β、R1和R2均为常量。该指标根据人的视觉观感与图像的低级特征评估图像特征的相似性。FSIM范围为[0,1],取值越大,说明分割越接近原始图像,质量也越好。 表2统计了在20次实验中GWO算法、IWOA算法、标准SHO算法以及本文的改进算法ISHO在4种基准函数上寻优得到的函数均值、标准方差、最小值和最大值。基准函数中,f1(x)、f2(x) 是单峰函数,f3(x)、f4(x) 是多峰函数。前者在整个搜索区域内仅有一个峰值(最优解),可以测试算法的收敛速度和求解精度;后者在整个搜索区域内存在多个峰值,可以测试算法摆脱局部最优的能力。均值和标准方差结果可以同步观察算法的寻优精度和稳定性。测试结果表明,ISHO算法在两种类型的基准函数测试中的寻优精度和稳定性都是表现最好的,这说明ISHO算法利用混沌映射初始化、收敛因子非线性调整、邻域重心对立学习机制对标准SHO算法的种群多样性改善、搜索与开发能力间的均衡,以及提升收敛速度和寻优精度的改进是切实有效可行的。 表2 算法在基准函数上的统计结果对比 图5是算法在基准函数上的寻优曲线,纵轴是目标函数均值的变化情况。可以看出,ISHO算法在4种基准函数上具有最快的收敛速度,在单峰函数和多峰函数中都取得了很好的性能。最终的寻优精度ISHO算法也是最高的,算法可以以最少的迭代次数使其收敛在最优解处。同时,在多峰函数的测试中可以看到,ISHO算法明显可以跳离局部最优,而对比算法则会收敛在局部最优解处而无法进一步提高寻优精度。 图5 收敛曲线 表3是4种算法计算的最优分割阈值。可见,分割阈值数较少时,3种算法在最优阈值选取上基本是保持一致的,这说明在较少阈值分割时图像分割的精度相差不大,但随着分割阈值数的增加,改进算法ISHO求解的阈值变得有所不同。然而,这无法表明算法所求解的阈值就是更加准确的,还需要进一步通过可量化的评估指标对算法的求解精度进行验证,即需要比较前文中的峰值信噪比PSNR和特征相似度FSIM两个指标。 表3 图像分割阈值 如图6、图7所示是3幅图像分割的PSNR和FSIM结果,为20次实验结果的均值折线图。从图6可以看出,分割阈值数从2~5时,ISHO算法的PSNR均值明显高于另外3种算法,且在不同阈值数下保持着优势,这说明ISHO算法具有较好的稳定性,算法求解的阈值更加准确,分割图像与原始图像具有更高的相似性,失真信息最少,可以更准确实现对目标区域的分割。对于House图和Coins图,GWO算法在选择较大阈值数时,得到的PSNR均值已经出现降低,说明算法的稳定性不足。在Persons图中,SHO算法的较大阈值数时,PSNR均值增长几乎停滞。从图7可以看出,ISHO算法的FSIM均值也明显高于另外3种算法。综合两项指标的统计结果,可以证明本文设计的ISHO算法应用在图像分割中,可以更加准确分割图像的目标区域,分割质量更高。 图6 峰值信噪比PSNR 图7 特征相似度FSIM 图8是3阈值时算法的图像分割效果。可以看出,ISHO算法的图像分割图失真是最少的,保留了原始图像中更多的细节信息,与原始图像的特征最为接近。具体地,在Persons图中,人物与背景中的家具边界分割显得更加清晰,家具的轮廓、边缘更加清晰。在House图中,房屋的砖块纹路更加明显清楚;Coins图中,各个硬币都被清晰的分割出来,且硬币的纹理效果有明显的提升。相比而言,GWO算法对Persons图分割效果较差,人物与背景模糊,Coins图中的部分硬币边界不清,纹理模糊。对于House图中,砖块边缘无法有效分割。IWOA算法和SHO算法在House图中的分割效果接近。而SHO算法对于Coins图的分割更好,硬币纹理比IWOA算法清晰。 图8 阈值数为3时不同算法的图像分割结果 图9是20次求解结果均值的关于Tsallis熵的收敛曲线图。黑实线条为本文的ISHO算法求解的结果。可以看到,在标准SHO算法的基础上,本文的ISHO算法实现了性能改进,同时稳定性较好。ISHO算法也是所有算法中得到的Tsallis熵值最大的,即适应度最大。SHO算法、IWOA算法、GWO算法较大可能会陷入局部优解,无法获取更好的适应度。从收敛曲线趋势观察,ISHO算法用了最小的迭代次数达到最优解,且后期一直保持平滑趋势,说明已经收敛。GWO算法和IWOA算法曲线趋势整体波动较大,部分曲线接近于阶梯形,而非上升式平滑曲线,说明算法性能稳定性欠佳。传统SHO算法多数迭代下处于平滑曲线,更新速度较慢,说明求解已经陷入局部最优。总体来说,ISHO算法不仅求解质量更高,而且收敛速度更快。 图9 Tsallis熵的收敛曲线 为提高图像分割的准度和精度,结合改进的鬣狗优化算法,设计了一种融合Tsallis熵的多阈值图像分割算法。首先,为了提高传统鬣狗优化算法的寻优精度和效率,利用混沌Tent映射生成初始种群,丰富种群多样性;引入非线性收敛因子调节机制,均衡全局搜索和局部开采能力;利用邻域重心对立学习机制计算对立解,以提高算法的全局寻优能力,避免算法陷入局部最优。然后,将设计的改进鬣狗优化算法应用于多阈值图像分割问题上,引用Tsallis熵作为评估搜索个体优劣和质量的适应度函数,通过启发式搜索的迭代寻优得到最优分割阈值。大规模图像分割实验结果表明,改进算法无论在图像分割直观图还是在定量指标上,都取得了预期效果。2 基于邻域重心对立学习的混沌鬣狗优化算法ISHO
2.1 混沌优化初始种群
2.2 收敛因子非线性调整
2.3 邻域重心对立学习
2.4 ISHO算法实现过程
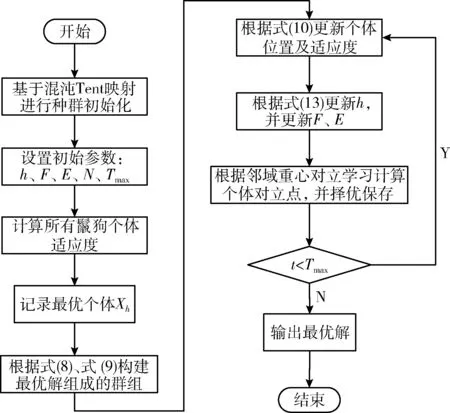
3 基于Tsallis熵的图像分割模型

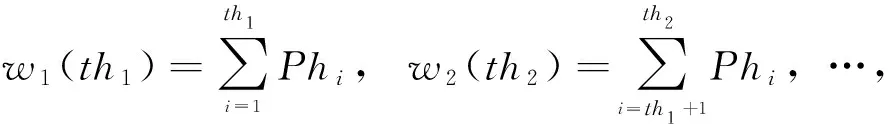
4 融合ISHO算法和Tsallis熵的图像分割
5 实验分析
5.1 实验环境及图像样本


5.2 图像分割指标
5.3 ISHO算法寻优实验结果
5.4 图像分割实验结果

6 结束语
