支持策略隐藏与撤销的属性基加密方案
2022-12-30吴正雪王静宇
吴正雪,王静宇
(内蒙古科技大学 信息工程学院,内蒙古 包头 014010)
0 引 言
云环境中通常使用基于密文策略的属性基加密技术[1](ciphertext-policy attribute-based encryption,CP-ABE),由用户制定访问策略加密明文数据,通过对访问策略的判定,实现一对多的数据安全共享。CP-ABE加密机制中,云服务器存储的密文信息中附带明文的访问策略,而实际应用中恶意用户能够通过公开的访问策略窃取用户的隐私。现有方案通过采用布隆过滤器[2]、双线性映射[3,4]、访问结构转换[5]、隐藏属性值[6]等技术实现访问策略的隐藏。但上述文献都未考虑到实际应用中用户属性动态变化的问题,为此大多方案通过更新属性版本密钥[7]、撤销列表嵌入到密文中[8,9]、更新属性群密钥[10]等方法实现属性撤销。但上述研究都不能确保密文数据的真实性与完整性,区块链技术[11-14]的提出能有效保证交易数据的安全性,具有不可篡改、不可伪造的特性,与加密技术结合能有效解决数据隐私问题。
为设计实现数据可靠性、访问策略隐私性和动态属性撤销,本文结合区块链技术,将对称解密密钥使用CP-ABE加密存储在云服务器中,数据摘要及文件位置等信息存储在区块链上,实现对数据的完整性审计,防止云服务器篡改数据。同时将访问策略转化为访问树结构,策略完全隐藏在密文中。当发生属性撤销时,由授权中心与云服务器进行密钥与密文的更新,减轻用户的计算开销。
1 相关知识
1.1 双线性映射

(1)双线性:对∀g∈G, ∀a,b∈Zp, 都有e(ga,gb)=e(g,g)ab。
(2)非退化性:e(g,g)≠1。
(3)可计算性:对∀g∈G, 存在一个有效的算法可计算e(g,g)。
1.2 密钥加密密钥树
密钥加密密钥树由属性管理器(AM)根据用户属性集合进行构建,其构建形式为一个完全二叉树——KEK树,如图1所示。每一个vj节点存储一个随机值θj,每一个用户uk与叶子节点相关联。通过计算从根节点到用户的路径节点Path(uk) 与最小覆盖集Mincs(Gi) 的交集,得到用户属性群密钥,其中属性群Gi代表拥有属性atti的用户集合。具体构建步骤请参考文献[15]。
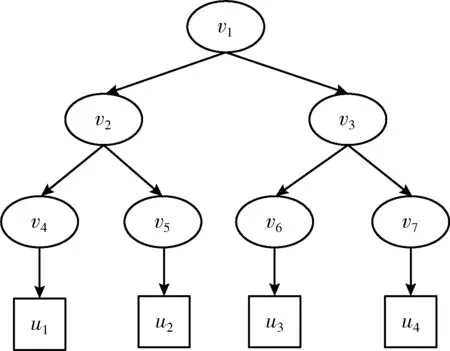
图1 密钥加密密钥树
1.3 实用拜占庭容错算法
本文区块链选取联盟链fabric 0.6版本,其采用的共识算法为实用拜占庭容错算法(practical byzantine fault tole-rance,PBFT)。PBFT共识过程分为4个阶段,首先客户端选取主节点,主节点对交易进行排序,并广播给其它节点,所有节点对交易进行验证,计算并广播其哈希值,节点之间进行哈希值的确认,当客户端收到f+1个节点的确认消息时,则将交易打包到新的区块中。具体共识步骤请参考文献[16]。
2 基本方案
2.1 系统模型
本模型中有6个角色,分别为数据拥有者(DO)、数据用户(DU)、云服务商(CSP)、可信授权中心(TA)以及区块链(BC)和属性管理器(AM)。如图2所示。
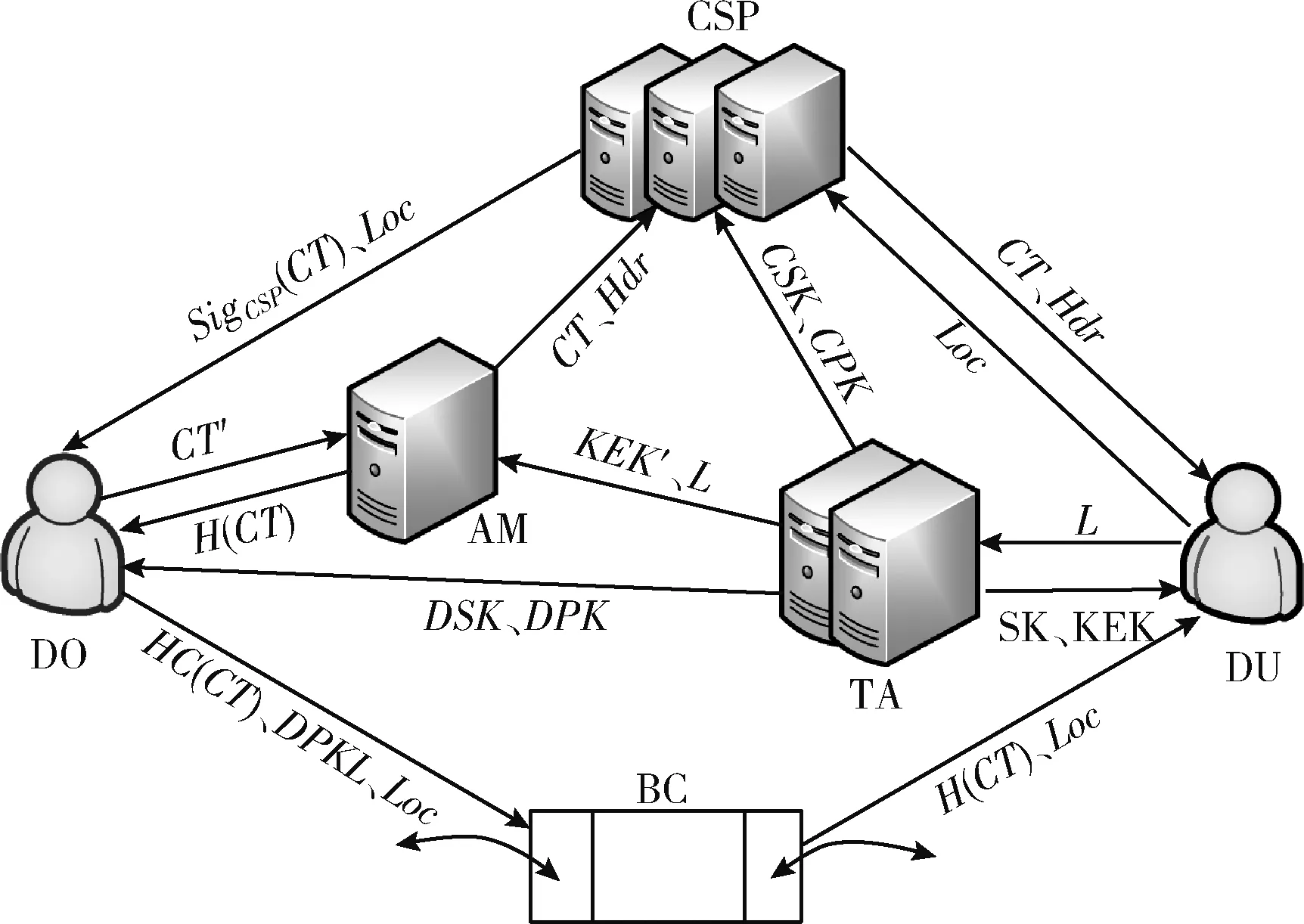
图2 系统模型
各个角色的具体介绍如下:
(1)DO:根据相应的访问策略加密数据,对交易数据进行签名。
(2)DU:请求访问数据,解密阶段可验证数据是否被篡改。
(3)CSP:负责存储加密数据,对密文哈希值进行签名。
(4)TA:负责系统初始化,为DU根据其属性集合生成私钥和属性群初始密钥。当发生属性撤销时,负责更新属性群密钥。
(5)BC:使用联盟区块链,区块链中每个区块包含密文的哈希值和密文存储位置。
(6)AM:负责密文重加密,当发生属性撤销时,AM执行密文更新算法,并且AM与CSP不会共谋。
2.2 算法定义
(1)系统初始化阶段。
TASetup(1λ,U)→(PK,MSK)。 由TA初始化系统。输入安全参数λ和属性集合U,生成系统公钥PK和系统主私钥MSK。
CSPSteup(PK)→(CPK,CSK)。 由TA执行,输入系统公钥PK,输出CSP的公钥CPK和私钥CSK。
DOSteup(PK)→(DPK,DSK)。 由TA执行,输入系统公钥PK,输出DO的公钥DPK和私钥DSK。
(2)密钥生成阶段。
TAKeygen(id,PK,MSK,L)→(SK,KEK′)。 TA执行算法,输入用户身份标志id、系统公钥PK、系统主私钥MSK和用户属性集合L,输出用户私钥SK和属性群初始密钥KEK′。
AMKekgen(KEK′,L)→KEK。 算法由AM执行,输入属性群初始密钥KEK′和用户属性集合L,输出属性群密钥KEK。
(3)数据文件加密阶段。
DOEnc(PK,Data,W)→CT′。 DO执行该算法,算法以系统公钥PK、明文数据文件Data和用户访问策略W作为输入,输出中间密文CT′。
AMRenc(PK,CT′)→(CT,Hdr)。 算法由AM执行。输入系统公钥PK和中间密文CT′,输出最终密文CT和密文头Hdr。
SignatureGen(CT)→(SigCSP(CT),Loc)。 CSP收到 (CT,Hdr) 之后,对CT进行签名,输出SigCSP(CT), 并将存储位置Loc发给DO。
(4)交易产生阶段。
TransGen(SigCSP(CT))→transaction。 DO根据CSP发送的SigCSP(CT), 进行密文的验证,验证成功则创建交易,将密文哈希值H(CT)、密文存储位置Loc和DO公钥DPK保存在交易,计算交易的哈希值H(trans),并向其它节点进行广播。
(5)解密阶段。
Decrypt(PK,SK,CT,Hdr,KEK)→Data。 由DU执行该算法,算法输入系统公钥PK、用户私钥SK、密文CT、密文头Hdr和属性群密钥KEK,输出明文信息Data。
(6)用户属性撤销阶段。
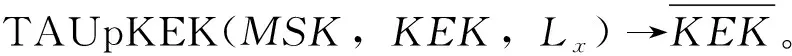

3 具体方案构造
(1)系统初始化阶段。

(1)
CSPSteup(PK)→(CPK,CSK)。 TA选择两个大素数p,q,并且计算n=p·q,φ(n) 表示n的欧拉函数。TA选择随机数E∈[1,φ(n)],E与φ(n) 互素。CSP计算 (D·E)modφ(n)≡1, 则输出CSP的公钥CPK={E,n} 和私钥CSK=D。
DOSteup(PK)→(DPK,DSK)。 与CSP公私钥生成方法相同,可以得到DO的公钥为DPK={E′,n′} 和私钥DSK=D′。
(2)密钥生成阶段。

AMKekgen(KEK′,L)→KEK。 算法根据1.2节中的方法为用户生成属性群密钥,对于Li=atti,bi, AM计算φi,bi=Path(uid)∩Mincs(Gi,bi), 若φi,bi=∅, 则停止计算;反之,计算KEKi,bi=(keki,bi)1/θj=gzi,bi·λi/θj,θj代表对应节点vj∈φi,bi, 输出KEK
KEK={Li,vj,keki,bi,KEKi,bi}Li∈L
(3)数据文件加密阶段。


2)如果孩子节点为未读状态,且非叶子节点为“或”门,则所有孩子节点值设置为s,并设置节点为已读状态。DO则计算
(2)
输出中间密文为CT′={W,C′,C′1,C′2,C′3,C′4}。
AMRenc(PK,CT′)→(CT,Hdr)。 AM得到DO发送的中间密文CT′,AM随机选择ki∈Zp, 并运行Mincs(Gi,bi) 算法,计算C4=C′4·∏i∈IWe(g,g)ki,C3=C′3,C2=C′2,C1=C′1,C=C′, 则密文与密文头为
(3)
AM计算密文CT的哈希值H(CT),并发送给DO,并将(CT,Hdr)发送给CSP存储。
SignatureGen(CT)→(SigCSP(CT),Loc)。 CSP收到(CT,Hdr)之后,计算CT的哈希值,得到H(CT),并且产生签名SigCSP(CT)=H(CT)Dmodn, CSP将SigCSP(CT) 和密文的存储位置Loc发送给DO。
(4)交易产生阶段。
TransGen(SigCSP(CT))→transaction。 首先DO得到CSP发送的SigCSP(CT), 验证SigCSP(CT)E=H(CT) 是否成立,如果成立,则CSP正确存储密文,DO创建交易,并将H(CT)、密文存储位置Loc和DO的公钥DPK保存在交易中,计算交易的哈希值H(trans),计算SigDO(trans)=H(trans)D′modn′。
DO提交交易,并向其它节点进行广播,区块链节点根据DO的公钥验证SigDO(trans)E′=H(trans) 是否与交易单存储的H(trans)相等,一样则说明交易数据没有问题,并发送给其它节点进行验证;否则,返回交易单。
(5)解密阶段。
Decrypt(PK,SK,CT,Hdr,KEK)→Data。
DU向区块链请求交易信息,区块链节点将交易单返回给DU,同时DU根据密文存储位置Loc向CSP请求密文,得到密文信息后,DU根据云服务器返回的密文,计算密文哈希值是否与区块链存储的哈希值H(CT)相等,相等则说明CSP返回结果是正确的。则DU按照如下过程进行解密
(4)
DU利用解密得到的对称密钥k,可得到明文文档,即Data=Dec(k,C)。
(6)用户属性撤销阶段。
当用户属性发生撤销时,TA对系统公钥、系统主私钥和属性密钥树进行更新,AM对密文进行更新。操作步骤如下:
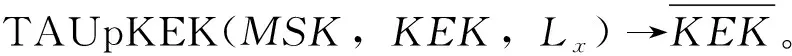


(5)
(6)
4 方案分析
4.1 安全性证明
定理:假设DBDH问题在群 (G,GT,g,p,e) 成立,至少存在多项式时间算法内以一个不能忽略的优势解决DBDH。
证明:假设敌手A攻破本方案的优势为ζ,则模拟器B就能以ζ/2的优势来解决问题,其中ζ是不可忽略的。
挑战者C在随机选取a,b,c∈Zp, 设θ∈{0,1}, 当θ=0时,计算Z=e(g,g)abc;θ=1时,则Z代表群GT上的一个随机值r。挑战者C将 (g,A=ga,B=gb,C=gc,Z) 发送给模拟器B。模拟器B充当挑战者C的角色,并执行以下过程。
(1)系统建立。敌手A将挑战访问树R、挑选的质询属性i*发送给模拟器B。
(2)初始化阶段。B定义系统属性集U,并且为每个属性atti∈Ux, 随机选取zi,bi∈Zp, 并计算Zi,bi=gzi,bi,Ti,bj=g1/zi,bi, 令α=ab, 则系统公钥为:PK={e,g,e(g,g)α,{Zi,bi,Ti,bi}1≤i≤n,1≤j≤ni}, 并发送给C,并创建列表K表示用户id存储的密钥查询。
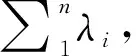


设置c为根节点的值,并标记为已读,所有的孩子节点设置为未读状态,则每个未读的非叶子节点进行如下递归运算:

2)如果孩子节点为未读状态,且非叶子节点为“或”门,则其所有孩子节点值设置为c,并设置节点为已读状态。模拟器B随机选择ki∈Zp, 计算
(7)
则CT={C1,C2,C3,C4}, 模拟器B生成密文头
(8)
模拟器B执行AMUpCT算法更新CT和Hdr
(9)
(10)
并将作为挑战密文的密文CT′={C′1,C′2,C′3,C′4} 和密文头Hdr′发送给敌手A。
(5)阶段2。同阶段1,但查询不到正确的密文解密私钥。
(6)猜测。敌手A输出关于θ的猜想为θ′。如果θ′=θ,则B输出0,则对应Z=e(g,g)abc, 密文CT有效,则敌手优势

(11)
反之,输出1,对应Z=r,密文CT对A来说是完全随机的,则
(12)
即选择明文攻击的游戏中,计算出模拟器B的优势为
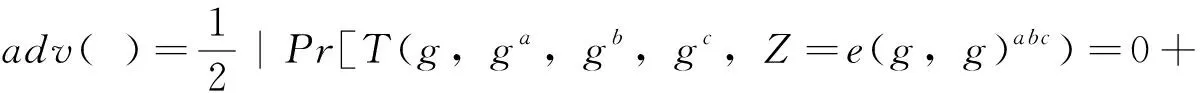
(13)
则模拟器B解决DBDH问题优势为ξ/2,基于上述过程证明系统的安全性。证毕。
4.2 性能分析
4.2.1 不同方案功能对比
如表1所示,本文与文献[5,9,10,14]的方案进行功能特征对比。文献[5]方案实现了策略隐藏,但在属性动态变化的场景里并不适用。文献[9,10,14]都支持属性撤销,但访问策略对所有用户可见,隐私安全性得不到保证,其中文献[14]方案通过结合区块链技术实现管理用户撤销列表,无需可信中心就能执行密钥的生成与更新。文献[9]和文献[14]支持LSSS访问策略,策略表达更灵活,但策略复杂,计算开销较大。虽然本文方案访问结构为树形,但在实际应用中是可以接受的。

表1 不同方案功能对比
综上所述,本文方案结合区块链技术,实现用户对数据完整性的可验证,保证了云服务器返回结果的正确性。方案不仅实现策略隐藏,并且实现了属性撤销功能,功能性较强。
4.2.2 不同方案存储开销对比
本文与文献[5,9,10,14]方案在存储开销进行对比分析,如表2所示。 |G1|、 |G2|、 |Zp| 分别表示群G、群GT、域Zp上的一个元素的长度,nu、na、nk分别代表系统、DO访问策略(LSSS和访问树)和DU的属性个数,|CK|、|KK|分别代表密文头、属性群密钥的长度,r代表撤销用户的数量。

表2 不同方案存储开销对比
TA存储开销主要是系统主私钥的长度。文献[5,9]方案系统主私钥长度为常数级别,文献[10]和本文方案存储代价随着系统属性数量线性变化。
DO存储开销主要取决于系统公钥长度。文献[10,14]方案使用较少的存储开销,文献[5,9]和本文方案系统公钥存储长度与系统属性数量有关。
CSP存储开销主要来自于密文和密文头。文献[5,9,10,14]方案密文长度与用户访问策略属性个数呈线性正相关,文献[10]与本文方案不仅存储密文,还要存储密文头,但本文方案中密文长度恒定,密文头长度随访问策略属性数量线性增长。
DU存储开销主要为密钥长度。由表看出,文献[5,9,10]和本文方案私钥存储与用户属性有关,并且文献[10]和本文方案需要额外存储属性群密钥,文献[14]方案采用外包解密技术,用户只需要存储最后的私钥就可,因此存储代价最小。
4.2.3 不同方案计算开销对比
基于CP-ABE的数据共享方案中,双线性配对和指数运算用来表示其计算性能,因此忽略哈希运算所消耗的时间,与文献[5,9,10,14]方案在加密和解密阶段的计算开销进行对比,如表3所示。其中,EG、EGT、p分别表示群G上的指数运算、群GT上的指数运算和1次双线性对操作,ns、nd分别代表DO访问策略和DU解密时需要的属性个数。

表3 不同方案计算开销对比
数据加密阶段,DO首先加密数据得到中间密文,其子项C′1和C′2计算开销为EG+EGT,C′3和C′4计算开销为ns(EG+p), 则总开销为: (ns+1)EG+EGT+nsp。 文献[5,9,10,14]与本文方案中DO加密计算开销都为线性变换,但文献[9,14]方案中变化的斜率较大。
用户解密过程中,数据使用者需要进行较多的双线性运算,其计算代价为: (nd+3)p+EGT。 其中,文献[14]方案中采用外包解密技术,计算开销最低。
从表3可以看出,本文与文献[5,9,10]方案加密计算代价都与用户访问策略属性个数相关,但本文方案解密效率较高。
4.3 性能测试
4.3.1 加解密时间消耗
本文与文献[5]和文献[10]方案在加密、解密阶段的时间消耗进行实验对比,方案采用JAVA中基于配对的密码学(JPBC)库进行仿真实验,具体的实验环境为Intel Core i7-8700 CPU处理器,内存为16 GB,操作系统为Windows10 64位。
实验使用Type A型的素数阶椭圆曲线,椭圆曲线为y2=x3+x,代码基于JPBC-FAME与ConstantSizeCPABESE进行修改编写。
本文方案主要是对用户的加解密时间消耗进行仿真。实验中,设置5种不同的访问策略,以10为属性增量,从10增加到50。不同的访问策略,数据取10次实验的平均值作为实验结果。
如图3所示,文献[5]和文献[10]方案加密消耗时间在相同属性数量下相似,但本文方案加密时间较长一些,因为在保证密文长度恒定时需要额外的双线性运算,计算开销较大,但存储开销较低。
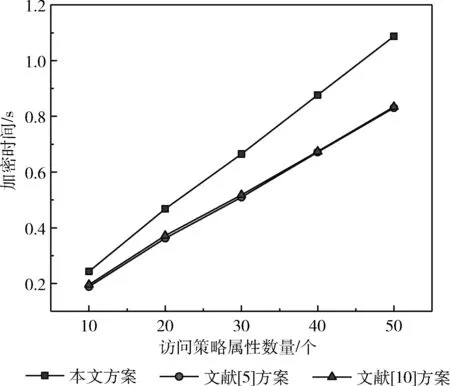
图3 加密时间对比
解密时间消耗对比如图4所示,解密消耗时间都随着解密属性数量增加而增加,但文献[5]和文献[10]方案中解密消耗时间变化的斜率较大,相同解密属性数量下本文解密消耗时间是最低的。
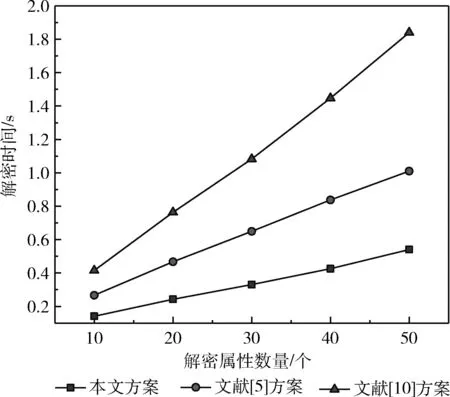
图4 解密时间对比
综上,本文方案属性撤销时密钥更新与密文更新由TA和AM执行,DO只参与加解密阶段,并且具有较高的解密效率。因此,方案对于属性频繁变动的场景是适用的。
4.3.2 PBFT算法通信次数分析
本文使用PBFT算法实现共识,当系统节点为n个时,在客户端请求阶段,通信次数为n次;预准备阶段,主节点与其它节点通信,次数为(n-1)次;准备阶段,每个节点都与其它节点进行通信,则通信次数为 (n-1)(n-1) 次;确认阶段需要n(n-1) 次;回复给客户端阶段需要n次,总通信次数为2n2次。通信次数图像如图5所示,并对函数进行取对数运算。可以看出,当节点达到一定数量时,通信次数会随着节点数量的增加缓慢上升。
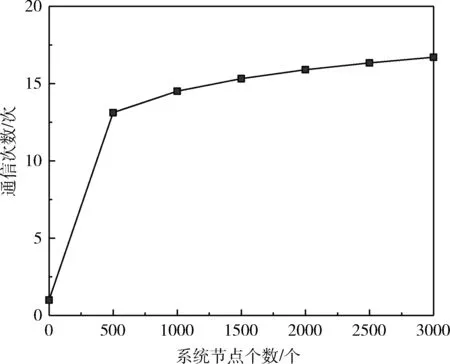
图5 PBFT算法通信次数
5 结束语
本文通过结合区块链技术,提出了支持策略隐藏与撤销的CP-ABE方案,用户不仅实现数据自主权,并且确保数据具有完整性、真实性。首先,明文形式的访问策略存在信息泄露的问题,因此实现策略隐藏是有必要的。其次,属性的即时撤销保证被撤销的用户无法获得数据的访问权。同时方案中恒定的密文长度,减轻了云服务器的存储负担。最后,在标准模型下,基于DBDH假设完成安全性证明。与同类方案对比,加解密效率较高,并且方案功能性较强,更符合当前云环境的需求。
