基于Spark的并行反向k最近邻查询
2022-12-30杨泽雪刘伟东
杨泽雪,张 毅,李 陆,刘伟东,蒋 超
(1.东北林业大学 信息与计算机工程学院,黑龙江 哈尔滨 150040;2.黑龙江省政务大数据中心 合作交流与创新发展处,黑龙江 哈尔滨 150028;3.黑龙江工程学院 计算机科学与技术系,黑龙江 哈尔滨 150050)
0 引 言
随着数据量的爆炸式增长,研究分布式环境下的并行反向k最近邻(reverseknearest neighbor,RkNN)查询[1]受到研究人员的关注。
目前流行的并行处理框架主要包括MapReduce和Spark。而当前的并行RkNN查询算法大多数都是基于Map-Reduce[2-5]框架。文献[6]介绍了基于倒排网格索引(inver-ted grid index)的分布式RkNN查询处理方法。文献[7]在Hadoop的空间扩展框架SpatialHadoop上进行了分布式RkNN查询研究,给出了基于SpatialHadoop的RkNN查询算法,并在真实数据集上实现了该算法。文献[8]提出了基于SpatialHadoop的RkNN查询MRSLICE算法。基于Spark框架的分布式空间查询研究,近年来国内外学者提出了GeoSpark[9]、SpatialSpark[10]、LocationSpark[11]等框架,这些框架可实现基于Spark的分布式空间范围查询、kNN查询和空间连接查询,并且通过实验验证基于Spark框架的查询处理优于MapReduce框架。除以上典型空间查询之外,学者们扩展了基于Spark框架的变体查询研究,包括距离连接查询[12,13]、时空连接查询[14,15]、top-k空间连接查询[16]、轨迹k近邻查询[17]、空间范围查询[18]、k近邻连接查询[19]、组k近邻查询[20]等。
以上研究均展示了Spark框架处理并行空间查询的优越性。但是,基于Spark框架的RkNN查询研究较少,文献[7]提出了基于LocationSpark的并行RkNN查询算法,并将该算法与基于SpatialHadoop的RkNN查询算法进行了比较,结果显示基于LocationSpark的并行RkNN算法明显优于SpatialHadoop。为此本文基于Spark框架研究并行RkNN查询,基于Voronoi图在空间邻近性方面的优良特性,在Spark框架上扩展基于Voronoi图的并行索引结构Grid-Voronoi-Index,在该索引结构上给出基于Spark的RkNN查询处理算法SV_RkNN,进一步提高并行RkNN的查询效率。
1 相关定义


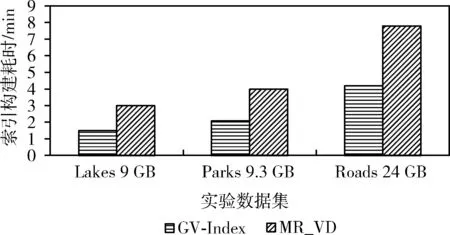
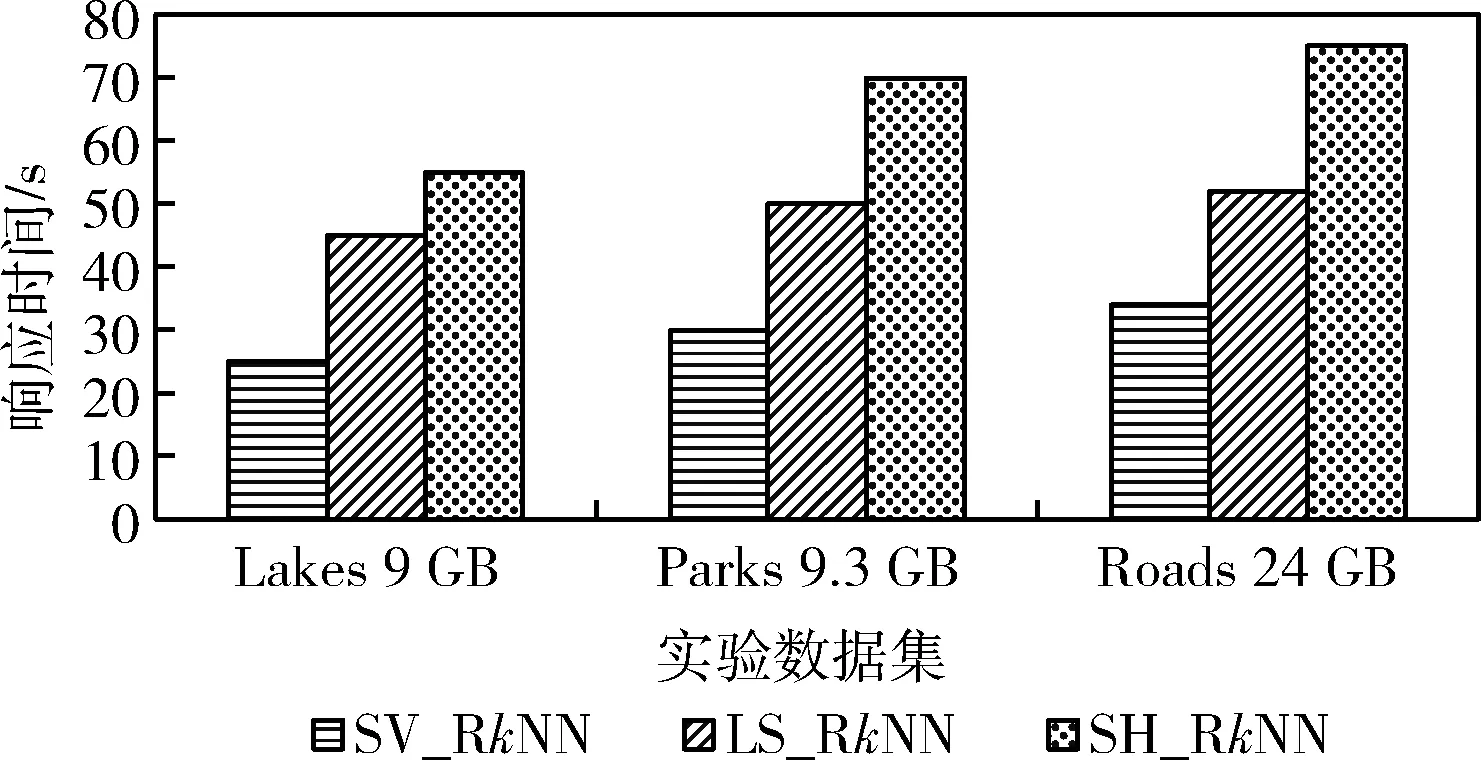
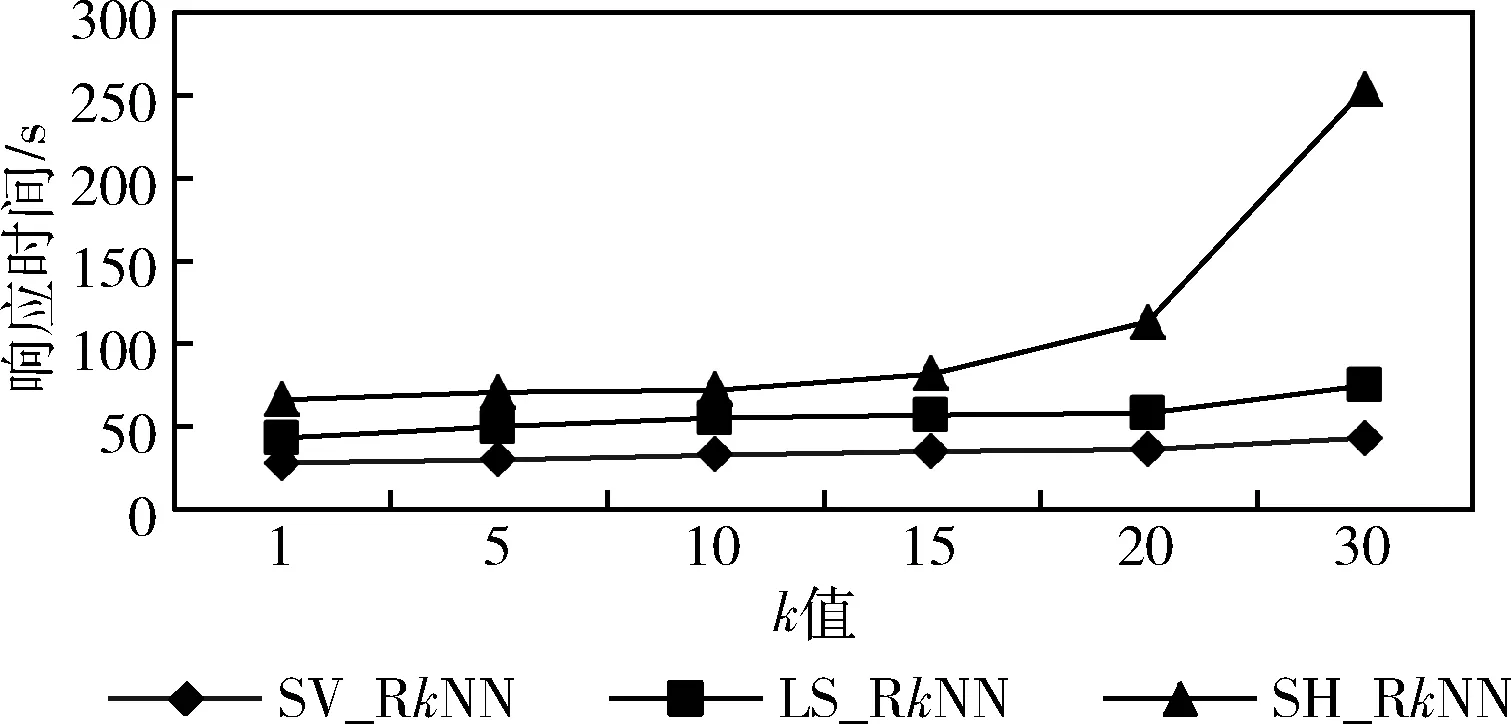
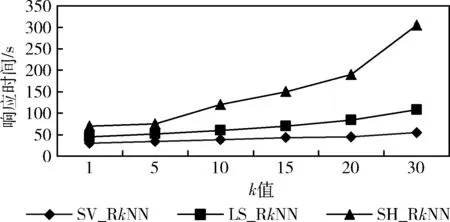
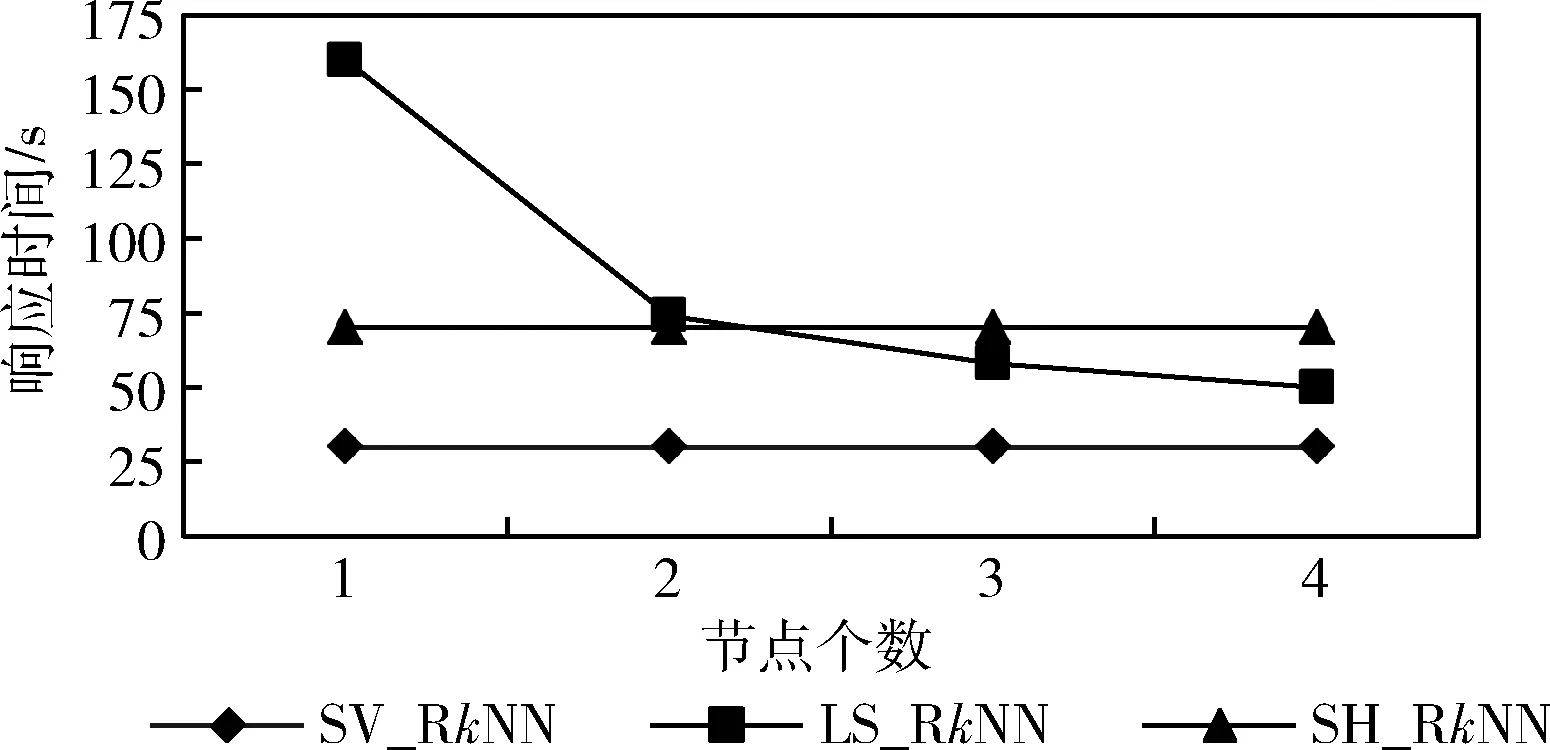
定义3[2]Voronoi图:给定一个点集P={p1,…,pn}, 其中2 定义4[2]k级邻接生成点:给定一组生成点P={p1,…,pn} 生成的Voronoi图中,其中2 AGk(pi)={pj|VP(p) 与VP(pj) 有公共边,p∈AGk-1(pi)} 定理1[21]给定数据集P的Voronoi图VD(P)和查询点q,其中q∈P, 查询点q的R1NN在其1级邻接生成点中。 推论1 给定数据集P的Voronoi图VD(P)和查询点q,其中q∈P,查询点q的RkNN在其前k级邻接生成点中。 定理2[22]给定数据集P和查询点q,在点q处将空间区域6等分(每个部分60°),则每个区域中查询点q的RkNN只能在其k近邻中。 为了完成并行反向k最近邻查询,构建双层索引结构,即全局索引和局部索引,全局索引采取网格索引,存放在master节点中,全局索引通过网格的划分将数据切分成各个数据块,然后在各个数据块上建立局部索引,局部索引采用Voronoi图索引结构,存储在各个worker结点中。基于Spark的网格-Voronoi图双层索引构建过程如图1所示。 图1 基于Spark的网格-Voronoi图双层索引结构 给定大规模数据集dataset,读取数据文件生成dataRDD并分配到各个分区中,此时的数据分区并没有考虑到空间数据的邻近性,而分区的数据关系直接影响到后续查询的性能。为此,将dataRDD重新分区,以保证数据的邻近关系。为此建立双层索引结构,首先对于dataRDD每个分区的数据进行采样,这里选取1%的数据,将这些数据传送到主结点生成网格索引GridIndex,然后利用网格索引将每个分区中的数据分配到对应的网格中,对于每个分区中的数据点,如果该数据点包含在某个网格中,就将其分到该网格中,分配结果生成新的网格分区RDD即GridPartitionRdd,然后将GridPartitionRdd中具有相同grid_id的数据重新分配到新的分区中,也就是进行再分区,对于每一个新的分区中的对象,分别建立Voronoi索引,形成VoronoiIndexRdd。 基于Spark的网格-Voronoi 图双层索引构建算法如算法1所示。 算法1:Grid-Voronoi-Index-Construct 输入:数据集dataset; 输出:局部Voronoi图索引,全局网格索引; begin sc←new SparkContext(conf); dataRDD←sc.textfile(dataset); //加载原始数据 SampleData←dataRDD.sample;//对原始数据进行并行采样 GridIndex←SampleData.CreateGridIndex; //基于采样数据,在master结点构建网格索引 for each partition do for each point in dataRDD do for each grid do If point∈grid then GridPartitionRdd← GridPartitionRdd∪(grid_id,point); //将dataRDD中的点分配到对应网格中 endif endfor endfor endfor rePartitionRdd←GridPartitionRdd.partitionBy (GridPartitionRdd(grid_id,point) ⟹rePartitionRdd(grid_id,point) //将具有相同grid_id的数据混洗到同一个分区中 for each partition do VoronoiIndexRdd←rePartitionRdd.map (rePartitionRdd(grid_id,point)⟹ VoronoiIndexRdd(grid_id,PVDi)); endfor VoronoiIndexRdd.merge(); VoronoiIndexRdd.cache(); GridIndex.cache(); return GridIndexRdd; return VoronoiIndexRdd; end 基于Spark的并行反向k最近邻查询处理过程如图2所示。 图2 基于Spark并行空间反向k最近邻查询处理流程 该查询方法首先载入数据集的全局网格索引,通过网格索引的检索,查找出包含查询点q的局部Voronoi图索引,加载局部Voronoi图索引,并启动任务开始执行。然后在每个分区中执行在基于Voronoi图的RkNN过滤-精炼算法,找到查询点q的RkNN,形成结果存储在HDFS中。 给定数据集P的Voronoi图VD(P)和查询点q,基于Voronoi图的RkNN过滤-精炼算法包含过滤和精炼两个步骤。首先,由过滤步骤获得可能成为结果的候选,在Voronoi图VD(P)中定位查询点q,在q处将空间划分为6等分区域,由推论1可知,查询点q的RkNN一定在其前k级邻接生成点中,再由定理2可知,每个6等分区域的RkNN结果只能在其k近邻中,因此对于每个区域,将q的前k级邻接生成点放入候选集中;然后,由精炼步骤去除候选集中不能成为结果的候选,计算候选集中每个点p的第k个最近邻k-thNN,如果p与k-thNN之间的距离小于p与q之间的距离,则从候选集中删掉p,最后将6个区域的候选集合并即为最终结果。 基于Voronoi图的RkNN过滤、精炼算法如算法2、算法3所示。 算法2: VRkNN-Filter(P,q,k) 输入: 查询点q, 数据点集P的Voronoi图VD(P), RkNN的k值; 输出: RkNN的候选集Scnd(i); begin fori=1 to 6 do Scnd(i)←∅; endfor 在VD(P)中定位查询点q; SixRegionPartition(P); for eachScnd(i) do for i=1 tokdo Scnd(i)←Scnd(i)+AGi(q); //将q的第i级邻接生成点加入候选集中 endfor returnScnd(i); end 算法3: VRkNN-Verification(P,q,k) 输入: 查询点q, 数据点集Voronoi图VD(P), RkNN的k值; 输出: RkNN结果集result; begin Scnd(i)←VRkNN-Filter(P,q,k); Scnd←∅; result←∅; for each pointpinScnd(i) do pk=k-th NN ofp; if dist(p,q)>dist(p,pk) then Scnd(i)←Scnd(i)-p; endif endfor Scnd←Scnd∪Scnd(i); result←Scnd; returnresult; end 定理3 算法VRkNN-Filter(P,q,k) 和VRkNN-Verification(P,q,k) 可以正确地查找查询点q的反向k最近邻,算法VRkNN-Filter(P,q,k) 和VRkNN-Verification(P,q,k) 是可以终止的,算法的时间复杂度是O(nlogn)。 证明:(正确性)算法VRkNN-Filter(P,q,k) 首先将空间区域以查询点q为中心进行6等分,然后在每个区域中查找q的k个最近邻,将这些结果放入候选集中,由推论1和定理2可知,算法VRkNN-Filter(P,q,k) 中的结果是正确的。算法VRkNN-Verification(P,q,k) 对候选集中的每个数据点进行处理,用该点的第k个最近邻与之对比,如果满足该点与查询点的距离大于该点与其第k个最近邻的距离,则去掉该候选,逐个去除错误的候选,得到正确的结果。 (可终止性)算法VRkNN-Filter(P,q,k) 对6个空间区域分别进行for循环,循环次数为k,是有限的,为此算法2是可终止的,算法VRkNN-Verification(P,q,k) 中的for循环是针对候选集中的对象的,数据也是有限的,所以循环是可以终止的,为此算法3也是可终止的。 (时间复杂度分析)算法VRkNN-Filter(P,q,k) 计算Voronoi图的时间复杂度为O(nlogn),在VD(P)中定位查询点q时间是O(logn),查找k个最近邻时间为O(klogn), 为此算法2的时间复杂度为O(nlogn+klogn); 算法VRkNN-Verification(P,q,k) 针对候选集中对象进行查询,假设候选集中对象个数为m,则查询时间为O(mlogn),为此算法3的时间复杂度为O(mlogn),综上,基于Voronoi图的RkNN过滤-精炼算法总的时间复杂度为O(nlogn+klogn+mlogn)。 证毕。 基于Spark的并行反向k最近邻查询算法SV_RkNN基本思想如下:算法包括两个步骤,第一个步骤为过滤,第二个步骤为精炼。给定双层索引结构的RDD,算法首先查询全局网格索引,定位查询点q所在网格,确定对应局部索引,在局部索引RDD所在分区执行过滤精炼步骤。过滤步骤执行VRkNN-Filter过滤算法,执行过程中如果出现候选集中的点在相邻的其它分区时,如图1的点p1的某些最近邻p2、p3在其相邻的分区中,需要对相应分区进行并行处理,再次执行VRkNN-Filter过滤算法,并将候选集进行合并,得到最终候选集;然后在候选集所在分区中执行VRkNN-Verification精炼算法,得到最终的并行反向k最近邻查询结果。算法SV_RkNN的数据流如图3所示。 图3 SV_RkNN的数据流 由图3可知,SV_RkNN查询处理算法包括Filter、Flatmap、Merge、Flatmap这4次转换,其中Filter转换可由全局网格索引定位查询点缩小查询范围,从而缩小中间生成的RDD大小,接下来的Flatmap转换完成过滤操作,产生窄依赖,而Merge转换完成再次过滤操作,产生宽依赖,会发生数据的混洗,但此时数据经过过滤已经极大缩小当前的RDD,最后的Flatmap转换完成精炼操作。此过程产生的中间RDD会在每次执行后删除,但索引RDD仍驻留在内存中,重复使用的索引RDD可大幅度加速迭代的执行。 基于Spark并行反向k最近邻查询算法如算法4所示。 算法4: SV_RkNN 输入: 网格索引GridIndex, Voronoi图索引VoronoiIndexRdd, 查询点集q, RkNN的k值; 输出: 查询集q的RkNN结果集合result; begin Grid_idArray←GridIndexQuery(q); //查询网格索引,确定查询点q所在网格,将对应grid_id记录在Grid_idArray中 VoronoiIndexRdd← VoronoiIndexRdd.Filter(grid_id); //根据Grid_idArray中的值确定相应局部索引 //过滤步骤 for the partition of VoronoiIndexRdd do CandidateSetRDD← VoronoiIndexRdd.flatmap(array⟹ VoronoiIndexRdd.VRkNN-Filter(P,qi,k)); Flag=0; for each pointpin CandidateSetRDD do ifpis in the neighboring partition do flag=1; partition←FINDPartition(P,p) endif endfor endfor if flag=1 do for each partition do CandidateSetRDD← VoronoiIndexRdd.Flatmap(array⟹ VoronoiIndexRdd.VRkNN-Filter(P,q,k)); endfor CandidateSetRDD.Merge(); endif //精炼步骤 for the partition of CandidateSetRDD do VerificationSetRDD← CandidateSetRDD.Flatmap(array⟹ CandidateSetRDD.VRkNN-Verification (P,q,k)); result.Initialize; result←VerificationSetRDD.reduce(); endfor returnresult; end 定理4 算法SV_RkNN的过滤步骤可以返回所有的结果(完备性),且算法SV_RkNN的精炼步骤返回的结果是正确的(正确性)。 证明:(完备性)SV_RkNN算法的过滤步骤可以产生所有的候选。因为算法的过滤步骤分成两个阶段,第一个阶段确定包含查询点所在的分区,执行一次VRkNN-Filter过滤算法,过滤掉不可能成为候选的对象,根据定理3可知,过滤掉的对象不可能成为候选。第二个阶段根据对象是否在其它的分区中,确定并行处理的分区,并再次进行VRkNN-Filter过滤处理,得到其它分区中的所有候选,并将所有候选合并为候选集,根据定理3可知,过滤掉的对象不可能成为候选,由此可知候选集中的对象包含了所有的结果,算法是完备的。 (正确性)SV_RkNN算法的精炼步骤不会删掉真正的结果并且不会返回的不是实际RkNN的结果。首先,算法对候选集中对象所在分区进行处理,执行VRkNN-Verification精炼算法,对候选集中的所有对象进行处理,删除错误的候选,根据定理3可知,删除的候选是不可能成为真正的结果,保证了结果的正确性。可以利用反证法来证明结果集中不会返回不是实际RkNN的结果。假设结果集中返回的点p不是实际RkNN的结果,则p的kNN中一定不包含查询点q,即p与q之间的距离一定大于p与其第k最近邻之间的距离,而这样的点在算法中一定会被删除,不能成为结果,所以与假设相矛盾,由此证明结果集中不会返回不是实际RkNN的结果。证毕。 实验是在一个包含4个节点的Spark分布式集群上进行,它由1个master节点和3个worker节点组成,每台机器的硬件配置都是:CPU型号为Intel CORE i5-104002.9 GHz六核处理器,内存为8 GB,硬盘1 TB。操作系统是64 位 Ubuntu16.04,Hadoop版本为2.7.1,JDK版本为1.7,Spark版本为2.0.1。 实验中使用二维点数据来测试所提出的SV_RkNN算法,实验数据来自于OpenStreetMap的3个数据集,这些数据集可以在SpatialHadoop官网[23]下载。数据集具体包括:Lakes、Parks和Roads。数据集详情见表1。 表1 实验数据集 实验测试构建索引性能,实验在不同分布数据集上分别比较本文创建索引算法GV-Index和文献[2]中基于Map-Reduce的Voronoi-based算法(称为MR_VD)的性能。 采用上述3个真实数据集进行实验,对比GV-Index算法和MR_VD算法构建索引耗时,实验结果如图4所示。由图4可知,对于每个数据集来说,GV-Index算法的构建索引耗时明显少于MR_VD算法的耗时,这是因为Spark基于内存计算的特点,可以在内存中进行数据缓存,节省了时间。 图4 数据集大小对索引构建耗时的影响 实验测试算法总的执行时间,即算法响应时间。实验在不同分布数据集上分别比较SV_RkNN算法和文献[7]中基于LocationSpark的RkNN算法(称为LS_RkNN)和文献[7]中的基于Spatial Hadoop的RkNN算法(称为SH_RkNN)的性能。 首先采用上述3个真实数据集进行实验,取k=5,分析数据集规模对算法的查询时间的影响。图5给出了SV_RkNN算法、LS_RkNN算法和SH_RkNN算法的响应时间随数据集大小的变化关系。由图5可知,数据集的大小对3种算法的响应时间的影响不大,算法具有较好的稳定性。这是因为,两种算法均采用了索引结构,而索引能够使得数据的查询范围缩小在限定的范围内,为此数据量的大小对响应时间的影响不大。但是,SV_RkNN算法的响应时间明显少于LS_RkNN算法和SH_RkNN算法,这主要是因SV_RkNN方法进行RkNN查询时,基于双层索引结构,通过全局索引的过滤确定局部分区,可以避免访问不必要的数据分区,只需在相关的数据分区内执行VRkNN查找,基于Voronoi图的性质3,一个点的Voronoi近邻最多为6,因此VRkNN中的kNN及每个候选点的第k个NN的查询分别只需访问6k个数据点,明显缩短了响应时间,效果较好。 图5 数据集大小对响应时间的影响 然后采用真实数据集Parks 和Roads进行实验,分析k值的变化对SV_RkNN算法、LS_RkNN算法和SH_RkNN算法响应时间的影响。实验选取k=1、5、10、15、20和30,实验结果分别如图6和图7所示。由图6和图7可知,k值的变化对SV_RkNN算法和LS_RkNN算法的影响明显小于k值的变化对LS_RkNN算法的影响。这是因为,随着k值的增大,候选数量明显增加,每一个分节点处理的数据量变大,SH_RkNN算法基于Spatial Hadoop,采取磁盘存储策略,读取大量的候选集需要多次的磁盘访问,增加了输入输出操作的代价。而SV_RkNN算法和LS_RkNN算法基于Spark,采用基于内存计算的策略,减少了磁盘访问的时间,查询过程中使用的数据直接可用,因此相对于k值的增大而言相应的执行时间变化不大。而对比SV_RkNN算法和LS_RkNN算法,由于LS_RkNN需要执行KNN查询(K远大于k),随着k值的增大,候选数量明显增加,而对于SV_RkNN算法,kNN及每个候选点的第k个NN的查询访问的数量分别为6k,因此随着k值的增大,SV_RkNN算法的性能优于LS_RkNN算法。 图6 Parks数据集k值变化对响应时间的影响 图7 Roads数据集k值变化对响应时间的影响 最后采用真实数据集Parks进行实验,取k=5,分析不同的计算节点数量对SV_RkNN算法、LS_RkNN算法和SH_RkNN算法响应时间的影响。实验选取节点个数分别为1、2、3、4,实验结果如图8所示。由图8可知,LS_RkNN算法的响应时间随着节点个数的增加而减少,并且随着节点数量越来越多,响应时间的减少幅度变小,这是因为节点数量的增加会增加节点之间的通信和调度时间,而且随着节点数量的增加,响应时间的减小幅度逐渐降低。但是,随着节点数量的增加,SV_RkNN算法和SH_RkNN算法的响应时间基本没有改变,而SV_RkNN算法的性能优于SH_RkNN算法,这是因为,通过全局索引确定分区后,RkNN的查找只在确定的分区进行,也就是说,由查询q的位置和k的值,可确定RkNN的查找通常在一个分区中进行,响应时间与节点的个数无关。 图8 节点个数的变化对响应时间的影响 本文对基于Spark框架的并行反向k最近邻查询进行研究,基于Voronoi图的良好特性,构建了基于网格-Voronoi图的双层索引机构,给出了索引构建算法,并在此索引结构上实现了基于Spark的并行反向k近邻查询,提出SV_RkNN算法,并通过真实数据集进行了实验,将SV_RkNN与基于LocationSpark的RkNN算法和基于SpatialHadoop的RkNN算法进行了比较,实验结果验证了SV_RkNN相对比较算法具有更好的查询性能和较好的稳定性。下一步计划研究基于Spark框架的空间连接查询,通过索引结构的改进,提高查询的性能。2 基于Spark的索引构建
2.1 基于Spark的索引构建过程
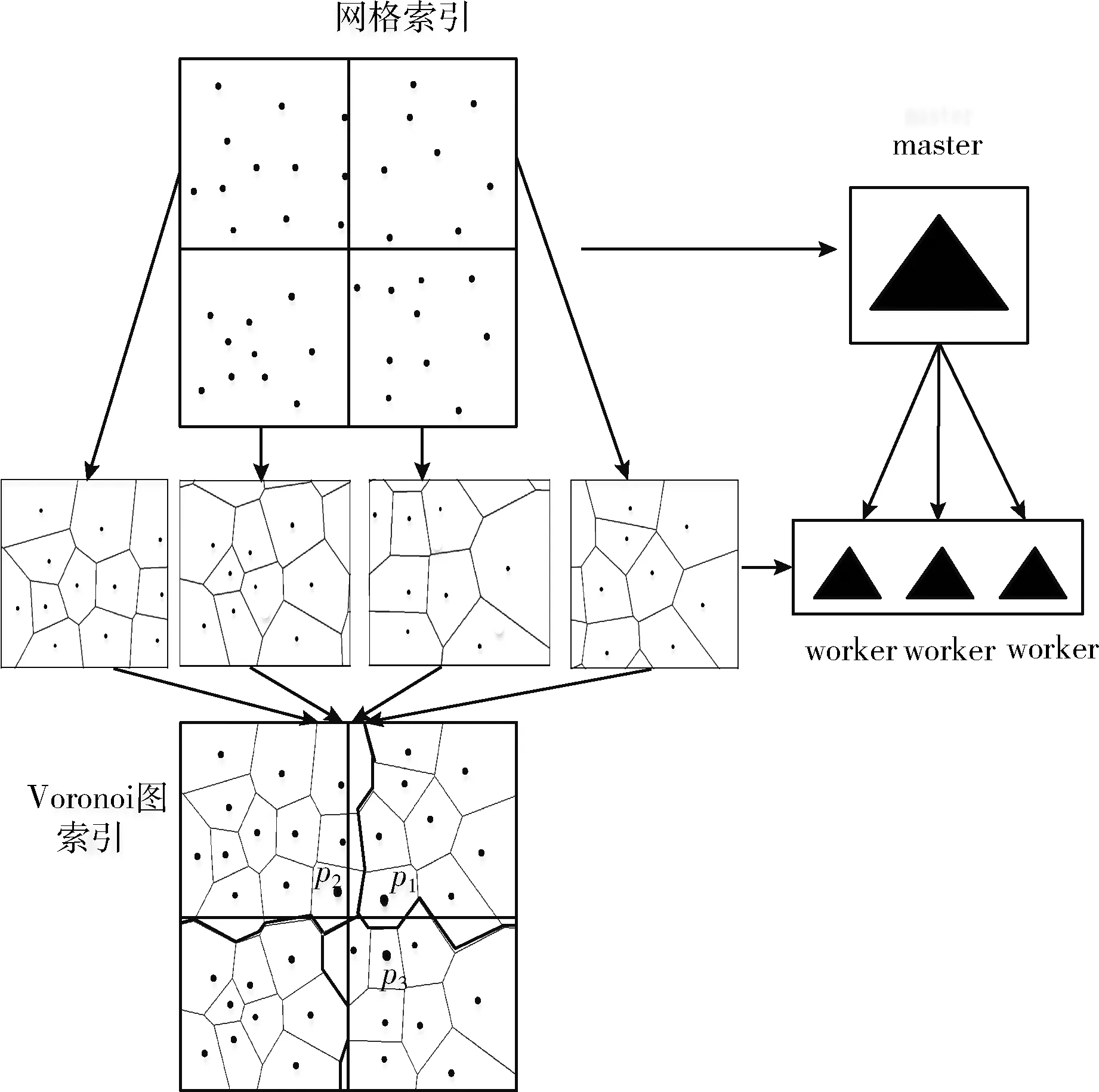
2.2 基于Spark的双层索引构建算法
3 基于Spark的并行反向k最近邻查询
3.1 基于Spark的并行反向k最近邻查询过程
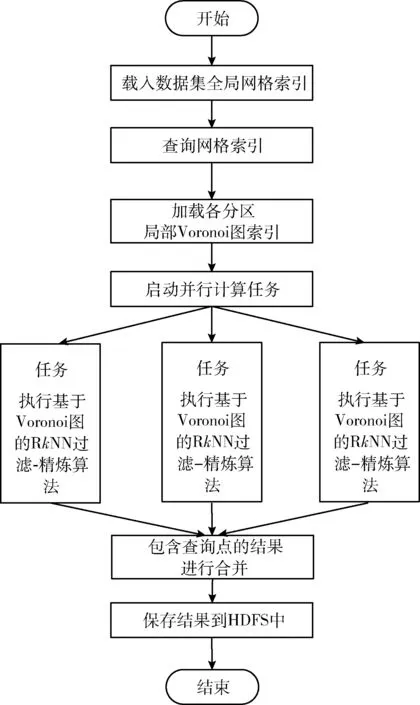
3.2 基于Voronoi图的RkNN过滤-精炼算法
3.3 基于Spark并行反向k最近邻查询算法
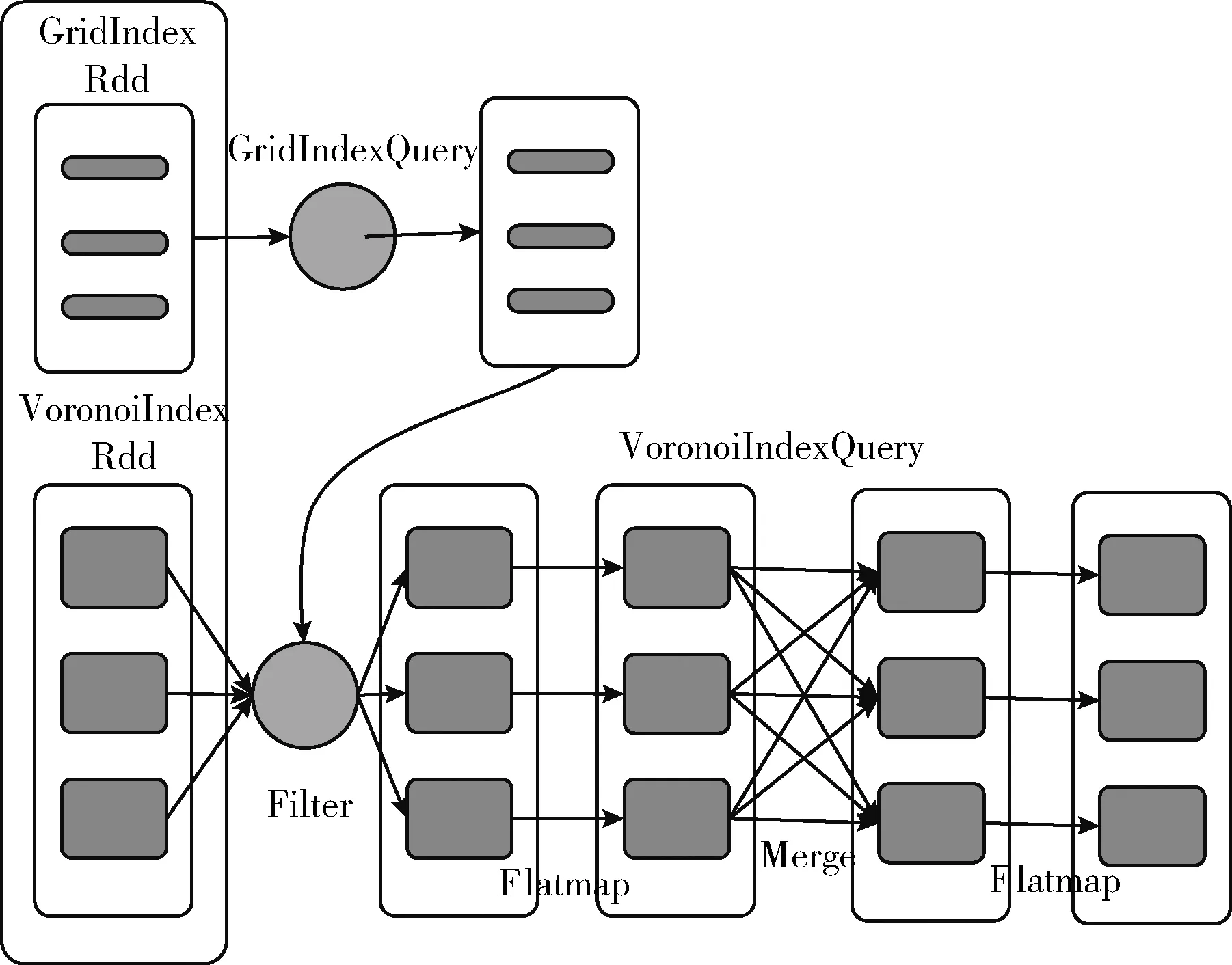
4 实验结果及分析

5 结束语
