基于马尔可夫理论的舰炮装备使用可用度预测方法

程文鑫，王寄明，郝兆钧

(1.海装装备项目管理中心，北京 100036；2.中国船舶工业系统工程研究院 武器系统研究所，北京 100191)

使用可用度是指某一武器系统或单个设备，在某种作战使用环境下，在任一随机时刻应召时，可以备便和满意地投入使用的预期时间百分比(是产品的能工作时间与能工作时间、不能工作时间的和之比[1])。因此，使用可用度是装备战备完好性的一个重要度量指标，表征了装备系统接收到作战命令时具备作战条件的能力。

对于使用可用度的分解，国内曾提出一种基于大量统计分析结果之上的模型，该分解方法属于解析法的一种[2]；而文献[3]则借鉴了传统可靠性模型理论，以可靠性公式相似的简化模型，对复杂系统的可用度进行分析，一般用于辅助制定保障决策，其精度难以保证。

对于舰炮装备，其作战使用具备以下几个特点：

1)产品组成复杂。现代化舰炮武器系统往往具有机电液系统耦合、多专业技术综合、多源信息融合等特点。

2)使用场景多样。即在厂家、岸边码头、近海区域、远海区域均有使用或维护场景。

3)多种维修体制。不仅可由舰员实施舰上的维修保障，亦可由相关维修保障部门在岸上实施维修，或返厂维修。

因此，对于舰炮装备，想要提前预知其在未来一段时间内的作战能力，需要考虑多种因素，较为困难。国内曾研究了一种基于备件库存的舰炮使用可用度建模与仿真方法，从三级备件库存结构和使用可用度着手，建立了使用可用度和备件保障度的关系模型，并进行了蒙特卡洛仿真[4]。

1 舰炮装备可用度评估方法概述

目前，国内关于可用度的评估，一部分学者从仿真的角度进行了大量的研究[5-7]。但这些研究尚未反映装备在执行任务中真实的使用场景和维修保障活动特点，以及保障资源之间的协作行为[8-9]。对于舰炮装备而言，目前可用度的预测主要是通过对使用数据进行统计、分析，计算其不同时间段的可用度估计值，然后采用线性拟合或者非线性拟合的方式给出其可用度的分布，从而实现对未来某时刻可用度的预测。此种方法需要事先约定以下假设：

1)装备的使用数据真实、有效，且满足一定的样本量要求；

2)在规定的时间内，装备维修保障活动符合一定的规律；

3)针对不同平台，其维修保障活动互相独立，不存在交互关系。

然而按照目前的装备维修保障现状，往往存在以下问题：一是装备的使用数据不满足要求，不仅装备的使用频次和强度较低，且使用者对数据的记录缺乏及时性；二是装备的修复性维修活动难以预测，因此无法在给定的时间段内对保障因素进行线性的分析；三是针对不同的装载平台，存在大量的保障资源借调使用的情况，这使得装备的保障活动分析难度大大增加，传统的可用度评估方法已经无法针对多种状态、多层次下的装备开展预测。

综上，现代化舰炮装备的可用度评估，必须紧密结合装备的多状态、多层次以及维修保障复杂的特点，研究更加贴合装备实际特点的方法开展可用度的预测。

2 舰炮装备的马尔可夫转移过程

马尔可夫过程(Markov process)是一类随机过程，通过表征已知系统的开始状态，以确定任意时刻系统所处状态的概率[10]。

考虑由L种不可修部件串联组成的多部件系统，每类部件的安装数量为Zi，每种部件的初始库存数为Si。不可修部件的备件需求产生时间与供应时间相互独立且服从指数分布，第i类部件的备件需求到达间隔时间服从参数为λi的指数分布，备件供应时间服从参数为τi的指数分布。

从系统级对多部件串联系统建模，因为是串联系统，只要有一个部件故障，系统便会立即停止工作。所以有L种部件，系统的故障状态便有L个。假设系统从正常工作到发生故障会经历L+1个典型的状态。系统的状态转移过程用随机过程{Y(t)=D(t);t≥0}表示，其中，D(t)表示t时刻系统处于的状态，D(t)∈{D0,D1,…,DL}，D0表示系统处于初始的完好状态(正常工作状态)；Di(1≤j≤L)表示系统因部件j故障导致的故障状态。多部件系统的状态转移过程如图1所示。αj表示系统从D0状态转移到Dj状态的转移率，βj表示系统从故障的Dj状态转移到D0状态的转移率，其中αj与βj需要进行库存充足过程状态归并处理之后计算得出，此部分将在下文分情况讨论。

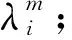
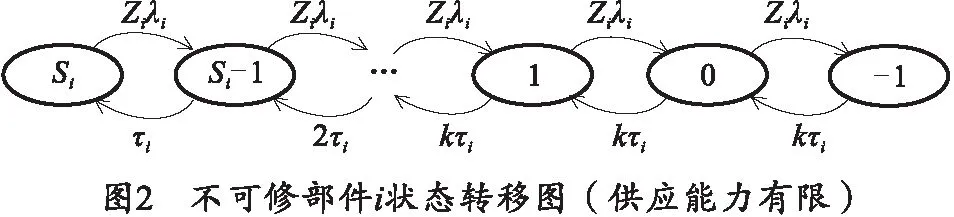
部件i在m状态的转移率表达式为

(1)

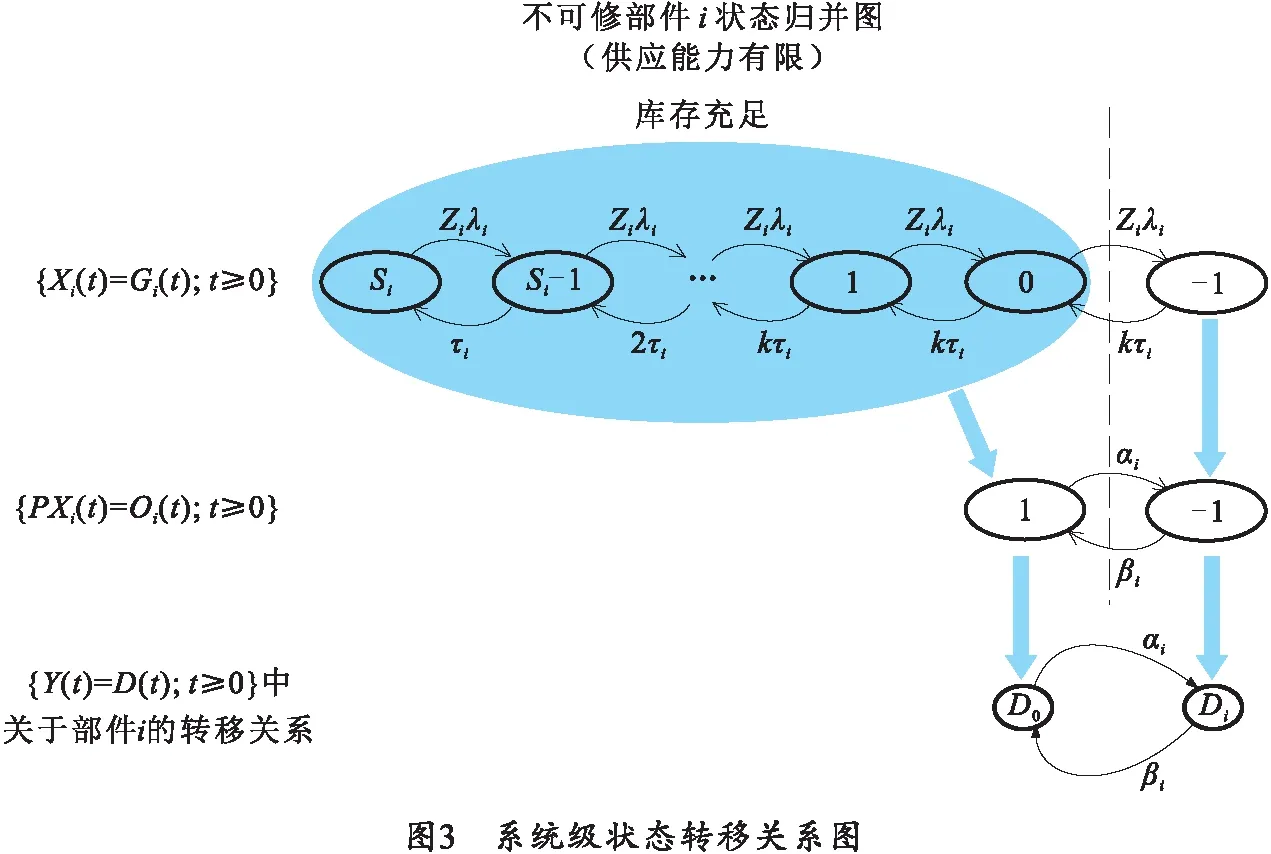
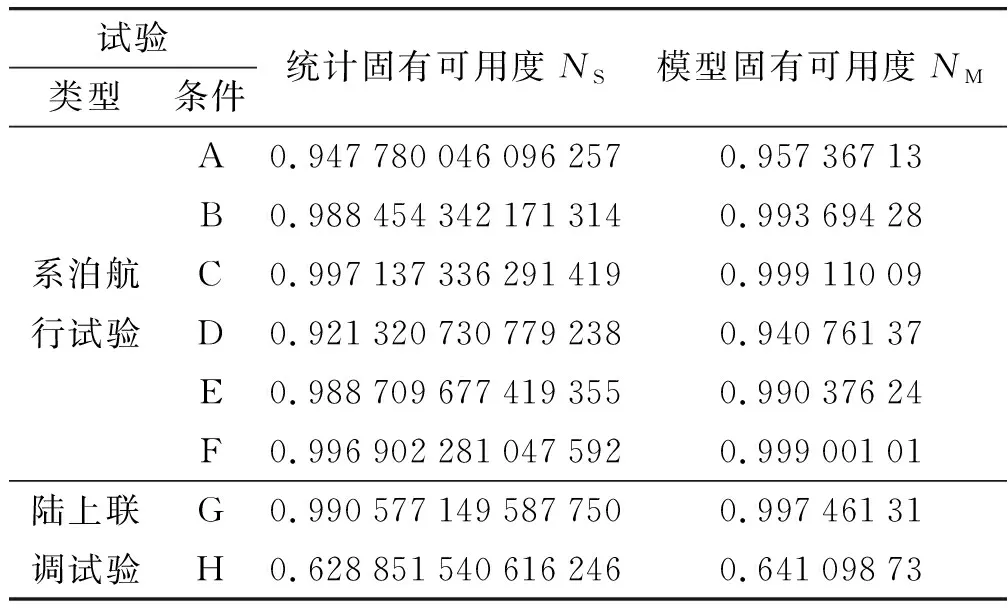
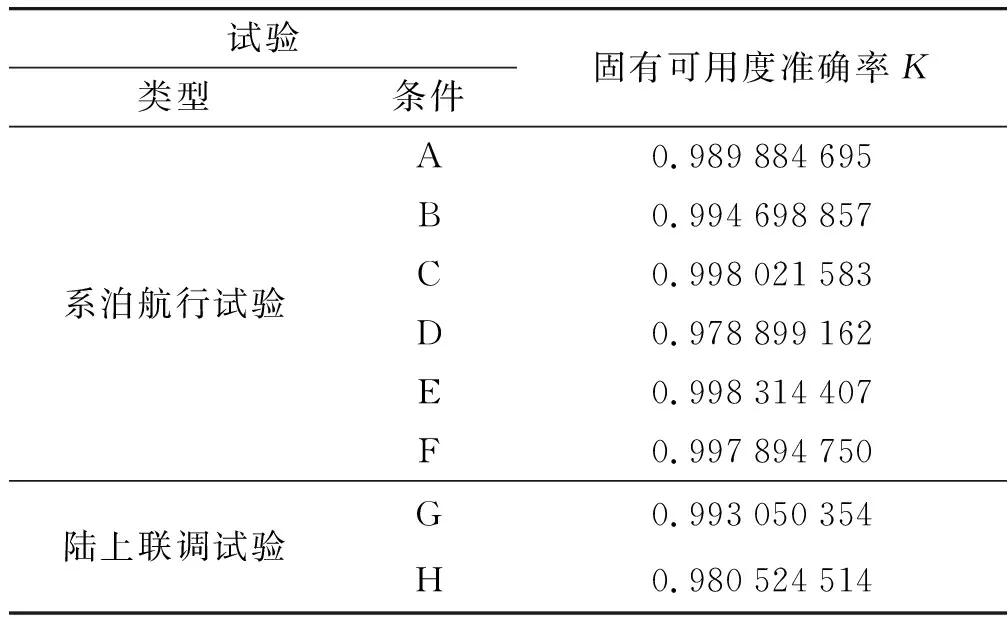
当0

(2)

(3)

需要对以上不可修部件i在供应能力有限的情况下的状态转移过程进行库存充足过程状态归并处理，即对随机过程{Xi(t)=Gi(t);t≥0}进行状态归并：将没有出现备件短缺(即备件库存数大于等于0)的状态归并为一个状态，这些状态的Si(t)≥0。对于其他状态，即出现备件短缺(即备件库存数小于0，导致系统不可用)的状态，则不进行任何操作。

将归并后的状态转移过程用一组新的连续时间马尔科夫链{PXi(t)=Oi(t);t≥0}来表示，其中，PXi(t)表示随机过程Xi(t)的马尔可夫链，Oi(t)表示系统可用数，因为此时研究对象为一个系统，所以此时Oi(t)也表示系统是否可用，当系统可用时，Oi(t)取值为1；否则为-1。归并后，3组马尔科夫链之间存在一定的转化关系，如图3所示。

3 舰炮装备可用度预测方法设计

基于前文的分析，可利用基于马尔可夫转移过程理论，对系统级的可用度预测方法进行设计。

步骤1给出其假设条件：

1)系统中各部件是串联结构，即只要有一个部件发生故障，系统就会立即停止工作；

2)可修件的故障间隔时间与维修时间相互独立且服从指数分布，第i类部件的故障间隔时间服从参数为λi的指数分布，维修时间服从参数为μi的指数分布；

3)不可修件的备件需求产生时间与供应时间相互独立且服从指数分布，第i类部件的备件需求到达间隔时间服从参数为λi的指数分布(部件因故障而产生需求，所以不可修件的备件需求到达时间等价于可修件的故障间隔时间)，备件供应时间服从参数为τi的指数分布；

4)采用的库存策略为及时送修策略，即(s-1,s)策略，只要部件发生故障，便立即送修或进行更换；

5)故障件的更换时间远小于备件的供应时间，忽略不计备件的更换时间；

6)系统工作时间连续；

7)部件的状态转移过程相互独立，互不影响。

步骤2用D(t)定义系统的状态，建立系统的马尔科夫状态转移过程。

步骤3用Di(t)定义部件i的状态，建立部件i的状态转移过程，并确定转移率矩阵Qi。

步骤4根据分析过程确定{Xi(t)=Gi(t);t≥0}、{PXi(t)=Oi(t);t≥0}以及{Y(t)=D(t);t≥0}这3组随机过程的转化关系。

步骤5利用3组的转化关系以及Qi，求解{Y(t)=D(t);t≥0}的转移率矩阵Q。

步骤6计算系统的瞬时概率矩阵P(t)，其中Ci表示部件i的马尔科夫模型状态集中的状态数。

(4)

步骤7通过方程组(5)计算系统的稳态概率矩阵π：

(5)

步骤8计算系统的瞬时可用度A(t)：

A(t)=p0(t).

(6)

步骤9计算系统的稳态可用度A：

A=π0.

(7)

4 可用度预测方法验证

为了验证笔者提出方法的准确性，收集了若干型舰炮装备的外场实装数据，分别通过统计学方法以及基于马尔可夫模型的预测方法，给出了各个装载平台下的可用度值。

对于统计固有可用度，即按照固有可用度的定义，对实装数据进行统计分析，计算得到系统的MTBF、MTTR后，根据固有可用度的计算公式Ao=MTBF/(MTBF+MTTR)进行计算，得到统计固有可用度的值，并作为真值，记为NS；对于模型固有可用度，即按照式(7)给出的稳态可用度公式，计算系统的模型固有可用度，并作为评估值，记为NM。

通过收集某使用方的实装数据，在系统级下计算了22个系统的统计固有可用度以及模型固有可用度，并以各试验类型进行统计分析，计算结果如表1所示。表中A～F代表不同试验条件下的系泊航行试验，G、H代表不同试验条件下的陆上联调试验。

表1 基于装备试验数据可用度计算结果

为了评估马尔可夫方法计算出的可靠性指标是否具有准确性，引入公式来对指标进行评估。准确率K的评估公式为

(8)

如果K>80%，则表明马尔可夫方法计算得出的可靠性指标是可信的。

按照式(8)计算基于试验数据的可用度的准确率K值，其结果如表2所示。

表2 基于试验数据可用度计算结果的K值对比

统计模型可用度比模型固有可用度计算出的数值稍低，但准确率K均超过80%；统计使用可用度比模型的使用可用度计算出的数值也稍低，准确率K也仍然超过80%。通过表2的结果可以看出，马尔可夫计算出的可靠度是可信的，在传统的统计学基础上做出了一定的变化，从而用另外的角度对舰队系统的可靠性、维修性等数据进行了评估预测，为今后的可靠性预测提供了理论基础和计算方法。

5 结束语

笔者以构建舰炮武器系统多部件状态转移过程为主体，构建不可修多部件系统的马尔可夫转移过程，然后基于马尔可夫状态转移过程，提出了系统可用度的预测方法，给出了其瞬时可用度和稳态可用度的求解方法。为了验证该方法的准确性，收集了某使用方的实装数据，并通过统计学方法计算了稳态可用度的真值，验证了模型可用度的求解准确率。

通过固有可用度评估的验证，舰炮武器系统多部件马尔可夫过程模型能够有效地反映舰炮武器系统在不同环境、任务剖面上的系统内各类部件及备件库存状态变化过程，更加准确地反映了舰炮武器系统使用可用度的动态变化情况，可为更完善地开展舰炮武器系统使用可用度评估工作中的数据收集、处理环节提供工程性指导。

笔者提出的基于马尔可夫理论的舰炮装备使用可用度预测方法为近似计算方法，且需要事先针对任务剖面进行重新拟定。如何充分利用系统任务过程中各单机的工作信息，精确地折算为系统任务信息，是未来对于系统可靠度评估工作研究的重点与热点内容。