基于非线性有限元的某车辆板簧系统失效分析
2022-12-30程瑞鹏刘丹杨雕郭旻李佳兴
程瑞鹏,刘丹,杨雕,郭旻,李佳兴
(1.陕西国防工业职业技术学院,陕西 西安 710300;2.内蒙古第一机械集团有限公司,内蒙古 包头 014033;3.西北机电工程研究所,陕西 咸阳 712099)
板簧是轮式车辆悬架的重要组成部分,在工作中主要通过承受轴向载荷作用而变形。变形时板簧各片之间由于相对滑动而产生摩擦,可以衰减车架振动,因此主要有减振和导向的作用,其不仅可以传递车轮与车架间的各种力和力矩,同时还可缓和因路面不平引起的冲击,对车辆的行驶有着重要的影响。
某轮式装甲车辆板簧系统由9个簧片组成,在野外跑车过程中经常因最底部和最顶部簧片出现裂纹或断裂而失效的问题,从而影响整个车辆的可靠性。目前对于多片板簧系统结构的受力分析主要有以下两种:一种是将其简化为悬臂梁,通过集中载荷法或共同曲率法等建立力学模型来进行计算板簧的受力及刚度;另一种是对板簧进行大量简化,并将其视为以中心螺栓孔左右对称结构,假设其前簧和后簧刚度相同,然后采用有限元的方法对其进行分析。以上几种方法都无法考虑板簧的真实工作受载情况,且某些板簧结构前后簧结构并不对称,实际受载变形过程中前簧与后簧会相互协调[1-4]。
笔者基于非线性有限元的方法,综合考虑其真实受载过程及边界条件,建立板簧系统非线性有限元模型,采用动静态耦合的方法,解决模型难以收敛的问题。首先计算U形螺栓预紧下板簧系统的变形及应力,在此基础上再考虑真实受载情况,获得板簧系统的整体变形及应力,以对其失效原因进行分析。计算结果表明,板簧刚度与实测值接近,最大应力出现的位置与实际工作中板簧出现裂纹及断裂位置相同,且应力值超过材料屈服极限,是板簧产生失效的主要原因。
1 板簧材料力学性能试验
由于板簧系统的工作环境为常温状态,且受载时应变率较低,因此根据国家标准GB/T 228.1—2010,在电子万能试验机上对板簧材料进行常温状态下的准静态拉伸试验,以测试其应力应变曲线,为板簧系统的失效分析提供材料参数。
试样选择原始直径为10 mm的圆截面比例试样,原始标距50 mm,试样总长100 mm,试样夹持方式为楔形夹具[5]。材料试样原始图如图1所示,试验后断裂图如图2所示,应力-应变曲线如图3所示。


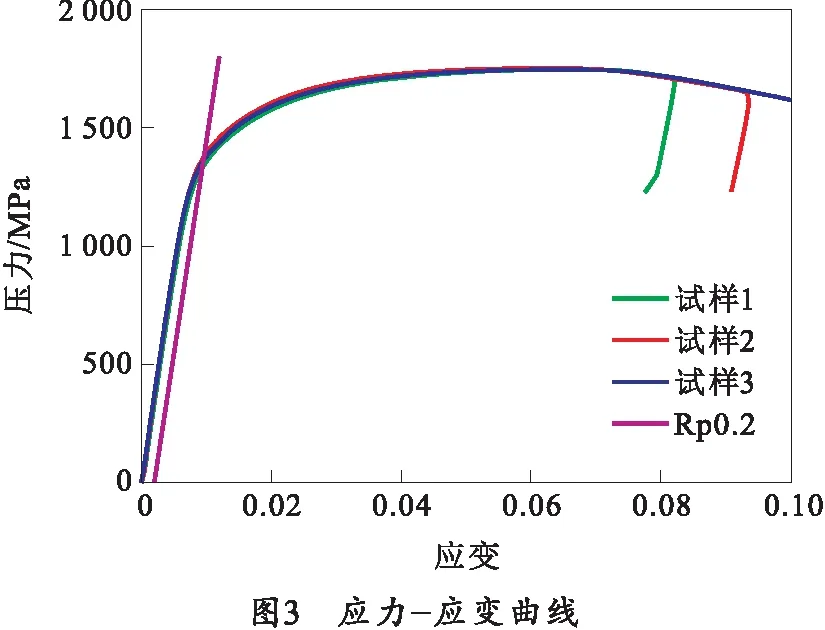
从图3中可以看出,3次试验应力-应变曲线一致性较好。取Rp0.2,即规定塑性延伸率0.2%时的应力为材料的屈服极限,3次试验材料的屈服极限及强度极限如表1所示。
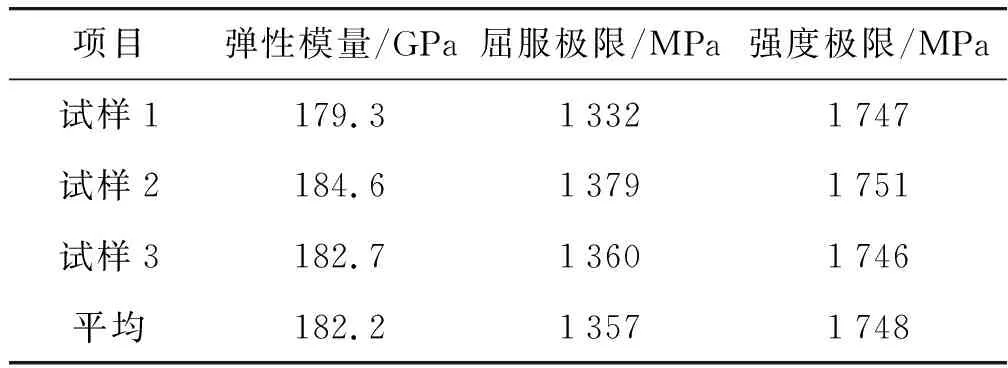
表1 材料弹性模量、屈服及强度极限
2 板簧非线性有限元模型
板簧的三维结构图如图4所示,板簧由前卷耳、后卷耳、吊耳、卡箍、U形螺栓、中心螺栓以及钢板弹簧片组成,该板簧共9个弹簧片。
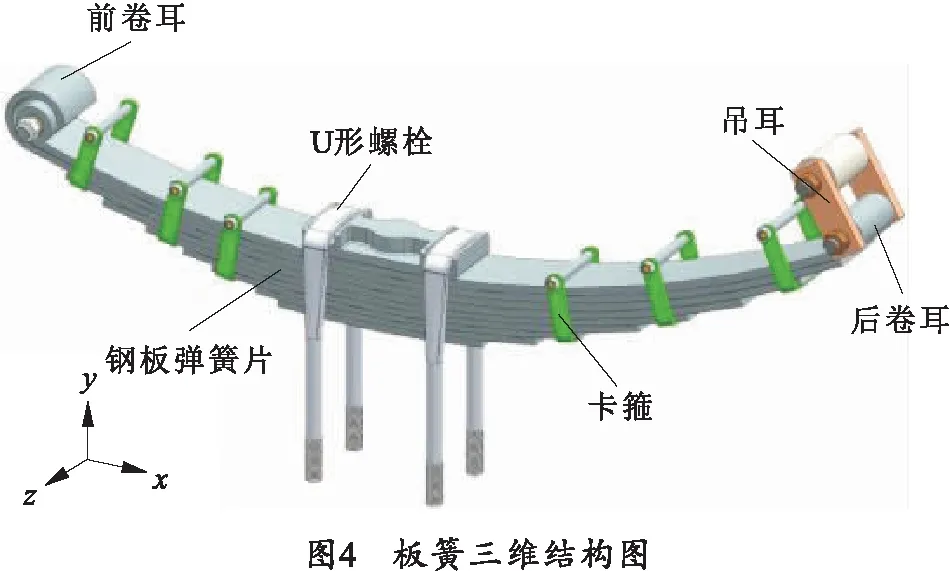
卡箍的作用在于限制板簧片的张开和其侧向滑移。中心螺栓位于板簧中心,用于固定各弹簧片。板簧在受载过程中,后卷耳可绕吊耳销钉转动。取板簧前卷耳到后卷耳水平方向为x轴正方向,板簧垂直方向向上为y轴正方向,如图4中所示。
2.1 有限元模型
板簧系统工作是变形较大、各板簧之间存在复杂的接触,属于强边界和几何非线性的问题,在计算中需对模型进行相应的简化,在减小模型的计算量的同时,应能确保计算结果不受影响。考虑板簧在簧片厚度方向上的对称性,取模型的一半进行计算。将板簧安装位置处以相同尺寸大小的垫块代替;并忽略吊耳的结构以等效的边界条件进行处理。由于模型在簧片厚度方向上对称处理,且整个计算过程均受压,忽略卡箍对板簧计算的影响。
考虑到模型计算过程的收敛问题,因此板簧结构的网格划分应该尽可能的规则,并对于可能发生接触的位置网格应该进行加密处理。故除了压板采用四面体网格外,其余结构全部采用六面体减缩积分单元,网格尺寸约6 mm,网格数约130 000,可进一步保证结构求解的精度。图5为板簧系统有限元网格图[6-7]。


2.2 材料参数
整个板簧系统材料相同,均为钢材料,计算时依据该材料实测参数将其简化为双线性模型,具体计算参数如表2所示。

表2 板簧材料参数
2.3 边界条件
板簧系统在使用过程中,经历了簧片的装配、装车及工作载荷3个过程。为了反映板簧的真实受力特性,在计算过程中也需要对其进行分步求解,分别为:
1)板簧簧片组装过程预应力分析;
2)存在装配预应力基础上进行装车及工作载荷加载。
在板簧对称面设置对称约束;在前、后卷耳中心建立耦合点将前、后卷耳上下位移进行耦合;在后卷耳与吊环之间施加耦合约束,约束除转动外的其余5个自由度,使后卷耳可绕吊耳转动;在板簧安装垫块底面施加固定约束;在板簧系统中有可能发生接触的地方定义标准接触[8]。
重力载荷以重力加速度进行施加大小为9 810 mm/s2;每个U形螺栓的预紧载荷为200 kN,分别施加到螺栓的中心轴线上;装车及工作载荷的极限值为48 kN,由于对模型进行对称简化,故载荷施加一半(24 kN)于前、后卷耳中心耦合点。
3 模型计算及验证
为解决仿真过程中板簧系统有限元模型的强边界非线性特性而导致计算不收敛的问题,在对模型进行U形螺栓预紧计算前,先施加一个较小的预紧载荷,并将该分析步设为隐式动力学计算。使得板簧系统各接触对在该分析步下逐步产生接触,然后再增加预紧载荷到实际值,进行U形螺栓预紧计算。
在隐式动力学计算中,施加的载荷不应太大且计算时间不能太短。太大的载荷会导致系统整体振幅较大,从而影响后续U形螺栓预紧计算时的结果,笔者施加的载荷为1 kN。较短的计算时间会导致由于动态载荷的施加而产生的动态效应无法衰减到稳定,具体计算时长应根据系统的固有频率、振型、阻尼决定[9],约为固有周期的10~20倍,笔者经过调试计算,时间取1 s。该分析步计算时,前、后卷耳中心处y方向位移曲线如图6所示。从曲线看出,在1 s左右,板簧卷耳中心位移趋于稳定,载荷的动态特性可忽略不计。
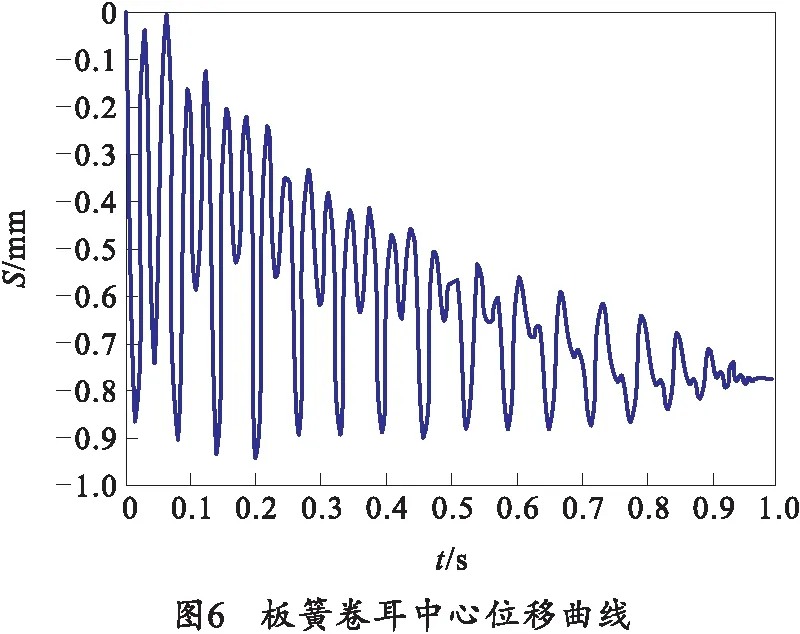
3.1 U形螺栓预紧计算
在上述隐式动力学计算的结果上,将U形螺栓预紧的载荷施加到实际大小,计算螺栓预紧后板簧系统的变形及应力状况,如图7、8所示。从计算结果可以看出,板簧系统在U形螺栓预紧载荷下前、后卷耳垂直方向(y方向)位移为24.3 mm,最大等效应力为1 280 MPa。

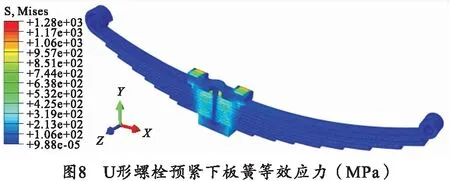
3.2 板簧受载计算
在U形螺栓预紧的基础上,对板簧系统进行受载计算。所受载荷为板簧系统装车时所受簧上结构的质量以及车辆行驶过程中其所受的工作载荷(取极限值)。由于两种载荷作用于板簧的位置相同,方向在同一直线上,故将两种载荷等效为一种,对板簧进行受载计算。板簧受载后y方向位移如图9所示,力-位移曲线如图10所示。
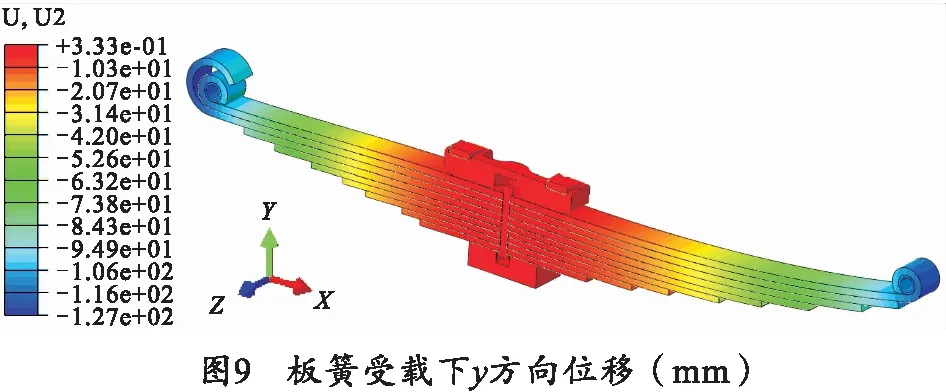
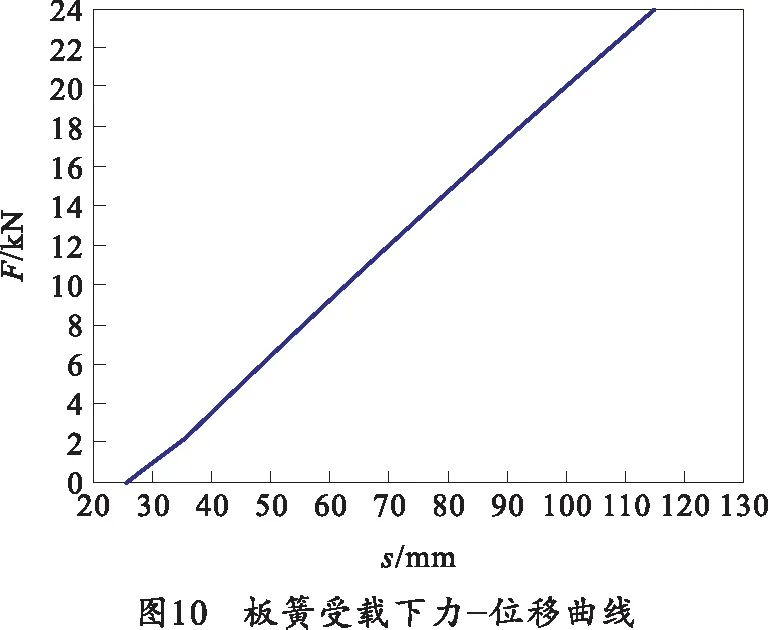
通过图9可以看出,板簧受载后前、后卷耳的y向最大位移为127.0 mm,受载前后的变化量为102.7 mm,与实测板簧系统最大行程103 mm基本相同。由图10可得板簧等效刚度为0.467 kN/mm。
3.3 模型验证
在试验台架上对U形螺栓预紧后的板簧施加48 kN的工作载荷,采用四分之一桥路,测量板簧第1块簧片不同位置处沿板簧长度方向的应变值[10]。应变片测试位置如图11所示。
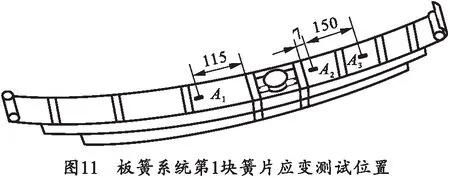
对板簧进行5次冲压,应变测试曲线如12所示,其中每一个冲压周期,波峰代表板簧基本上恢复到自由状态时的应变示值,波谷代表板簧的最大压伸应变。
对5次测试应变值取平均,与计算结果进行对比。由于试验是以预紧后的板簧为初始状态进行试验,因此仿真计算结果应取受载后的应变减去预紧应变,如表3所示,最大误差为8.7%。
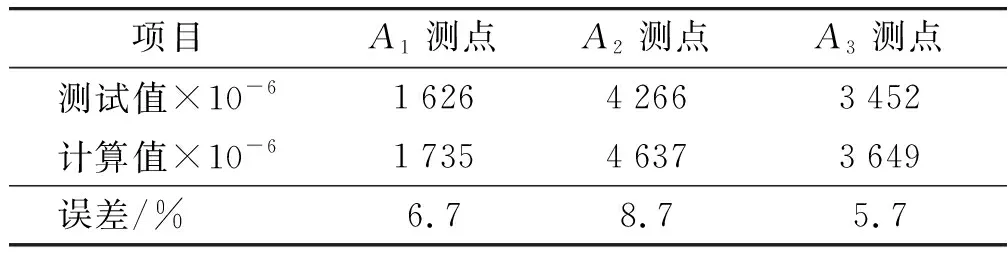
表3 仿真与测试结果对比
4 板簧计算结果分析
设板簧各簧片从上自下依次为第1到第9块簧片,应力超过材料屈服极限的簧片计算结果如图13~15所示。
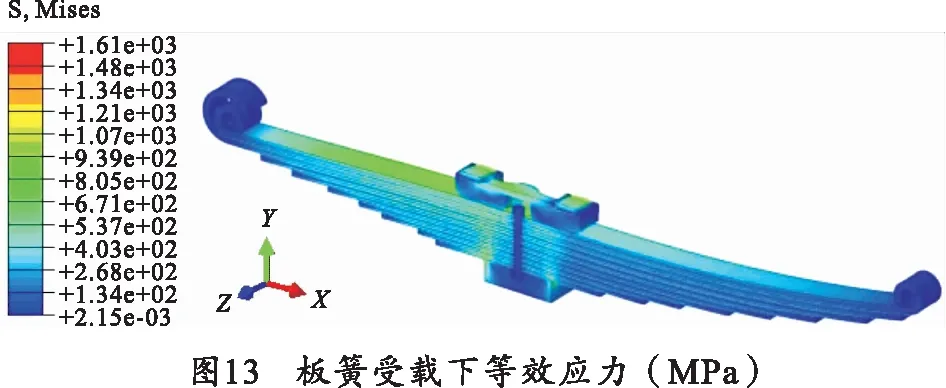
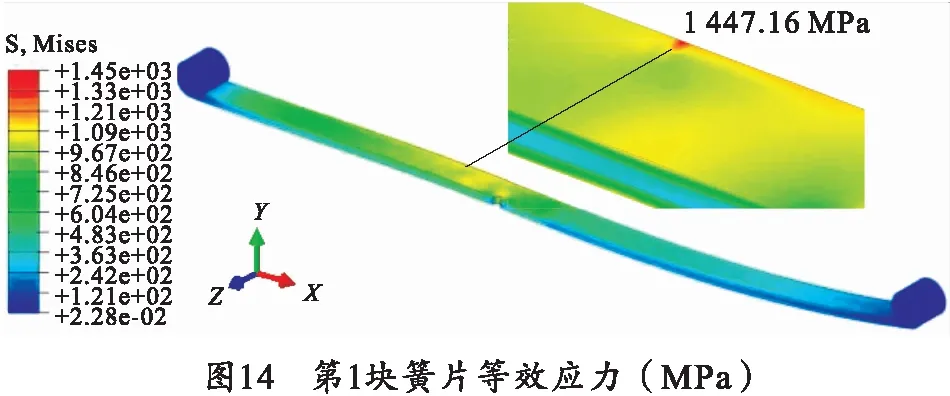
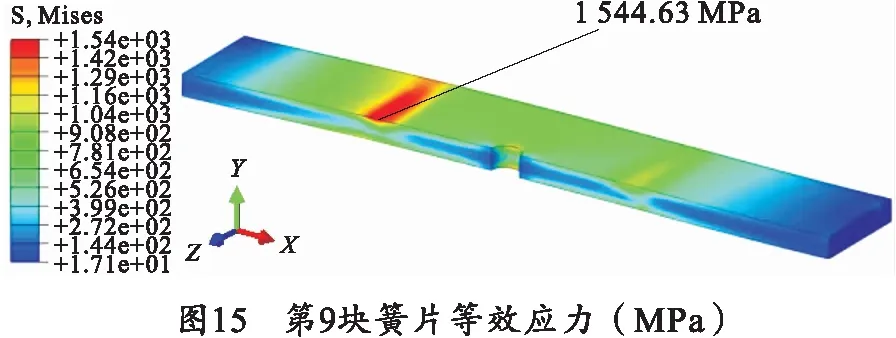
从计算结果可以看出,板簧在U形螺栓预紧和受载后最大等效应力为1 610 MPa。其各簧片中第1块簧片和第9块簧片的最大等效应力超出材料屈服极限,分别为1 447.16 MPa和1 544.63 MPa;且应力超出屈服极限的位置与板簧实际出现裂纹位置接近,如图16所示。

5 结论
笔者针对某车辆板簧系统在使用过程中簧片出现裂纹及断裂问题,建立了板簧系统非线性有限元模型,考虑了板簧预紧、安装及实际工作等过程,解决了模型收敛困难的问题,获得了其应力分布规律,通过试验测试验证了计算模型的精度,对其失效原因进行了准确定位。主要结论如下:
1)采用瞬态与稳态计算结合的方法,解决了板簧系统在U形螺栓预紧下的收敛计算问题,预紧后前后卷耳垂直位移为24.3 mm,最大等效应力为1 280 MPa。
2)板簧系统实际受载下最大垂直位移为102.7 mm,与实测103.0 mm基本相同;应变测试及计算最大误差为8.7%。
3)实际工作中板簧系统第1块簧片和第9块簧片的最大等效应力分别为1 447.16 MPa和1 544.63 MPa,超出材料屈服极限,是出现裂纹及断裂的主要原因。应力超出屈服极限的位置与板簧实际出现裂纹位置基本相同。
