基于小位移旋量公差建模和蒙特卡洛模拟的装配体公差优化设计方法

李晓晓，吴昊荣，孙付春，赵永鑫

(1.成都大学机械工程学院，四川成都 610106；2.成都大学电子信息与电气工程学院，四川成都 610106)

0 前言

工程图纸上大量的几何信息，一直缺乏标准化和规范化的分析手段[1]，传统的尺寸链计算方法已不能适应现代产品设计的要求。国内外学者对于装配公差分析进行了诸多研究，提出了多种分析模型。KENNETH等[2]提出了一种考虑几何偏差和装配偏差的非线性隐式装配关系的直接线性方法模型，通过二/三维公差分析方法，给出了三维公差分析方法的优势。MUJEZINOVIC等[3]提出了T-Map模型，可将特征公差带用多维参数空间来表示，但只能处理简单的公差链。GHIE等[4]将小位移旋量(Small Displacement Torsors, SDT)模型与雅克比模型结合起来，提出了用区间算法确定误差分析的雅克比旋量模型。ZUO等[5]提出一种多操作单步安装和多操作多步安装在工件固定装配中的基于约束的公差分析方法，对不同的误差源进行SDT建模，然后得到误差累计模型，进而确定最终的误差累计模型对加工特征在位置和方向上的影响。LI等[6]提出了基于SDT和偏差传播理论的机械装配公差分析方法，给出了集公差偏差建模、特征偏差建模和质量描述分析为一体的公差分析方案。ZHOU等[7]考虑以制造、运动、力方向和振动引起的偏差来模拟产品的运动学性能，基于偏差传播和小位移旋量的动态精度分析技术，同时提出两种新算法，用于解决力的方向和振动对偏差的影响以及描述运动位移产生的偏差。SUN等[8]为实现高精度和低成本的装配，建立基于三维统计公差的装配精度成本模型。

已有的公差分析方法缺乏对装配综合误差形成机制方面的研究。考虑到加工误差和装配误差均会影响装配体的装配精度，以装配结合面为研究对象，利用SDT理论和蒙特卡洛模拟法建立公差模型，再利用齐次变换理论建立结合面误差模型和装配精度模型，进而推导出机床静态几何精度与结合面公差相关的映射模型，最后结合公差制造成本、装配精度可靠度和公差原则，提出装配体静态几何精度优化的公差模型。具体工作流程如图1所示。

图1 基于SDT公差建模和蒙特卡洛模拟的装配体公差优化设计方法工作流程

1 装配体几何精度优化设计方法

装配体几何精度设计过程中包含三个重要因素：装配精度链、重要结合面和结合面公差[9]，可根据公差、结合面和装配链之间的传递关系，构建装配体装配精度与结合面公差相关的映射模型，以量化分析结合面公差对装配精度的影响程度。下面对SDT公差模型、结合面误差模型和装配精度模型的形成机制和建模过程进行说明。

1.1 基于SDT理论和蒙特卡洛模拟的公差建模

产品几何技术规范中将物体表面抽象为点、线、面等基本要素，其相对于名义位置的变动量均可用小位移旋量表示，即使用D=(α,β,γ,u,v,w)表示几何特征公差实际表面相对于名义位置的偏差[10]。此节以工程中常用的第I类平面定位尺寸公差为例，给出基于SDT理论和蒙特卡洛模拟的公差建模过程，主要内容包括公差域描述、SDT参数表达、约束方程推导和蒙特卡洛模拟求解。

(1)SDT参数表达以及约束不等式推导。第I类平面定位尺寸公差带如图2所示，图中局部坐标系原点位于平面中心，其z轴平行于平面法向；D为基本尺寸；TU、TL分别表示公差带的上、下偏差；变动平面z(x,y)对应的SDT形式[11]为(α,β,0,0,0,w)。根据公差域边界条件，变动平面的约束方程和位置变动方程如下：

(1)

式中：Δz(x,y)为任意两点在变动平面z(x,y)上的z值之差。

如图2所示，z的极值必位于矩阵平面的4个顶点上，故只需考虑变动平面的4个顶点A、B、C、D的z值是否在公差域内即可。由式(1)可得第I类平面定位尺寸公差的SDT旋量参数的变动不等式和约束不等式：

图2 第I类平面定位尺寸公差带

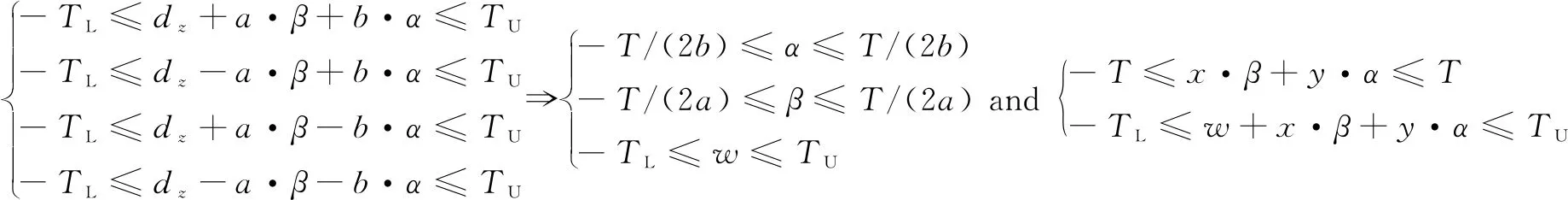
(2)

(2)利用蒙特卡洛模拟求解尺寸公差的SDT旋量参数

根据尺寸公差的SDT旋量参数变动不等式和约束不等式，可利用蒙特卡洛模拟得到足够数量且满足条件的随机样本。求解步骤如下：(1)考虑到尺寸误差的加工条件和产生机制，设定尺寸公差SDT参数符合正态分布规律，正态分布曲线的有效分布范围为6σ，分布中心与变动区间的中心重合，那么尺寸公差SDT参数α、β、w的理想分布均值和标准差分别为(0，T/(6b))、(0，T/(6a))、((TU-TL)/2，T/6)；(2)对旋量参数抽样进行模拟试验，抽样过程如图3所示(图中K表示最大抽样次数，k表示当前抽样次数，当k达到最大抽样次数时，程序结束)；(3)利用χ2拟合检验法检验旋量参数的实际分布类型，详细计算过程可参考文献[12]。

图3 尺寸公差SDT参数α、β、w的抽样试验过程

1.2 装配平面的结合面误差建模

在产品装配时，若能掌握每个零件在组装过程中偏差传递的累积规律，就可以定量地分析零件精度对装配精度的影响[13]，因此需建立装配过程中偏差传递的数学模型。以平面结合面为例说明装配过程中结合面误差的形成机制，参考图4，装配误差为理想装配平面PB相对于理想基准装配平面PA之间的位姿变化，误差传递关系为PA→PA′→PB′→PB。

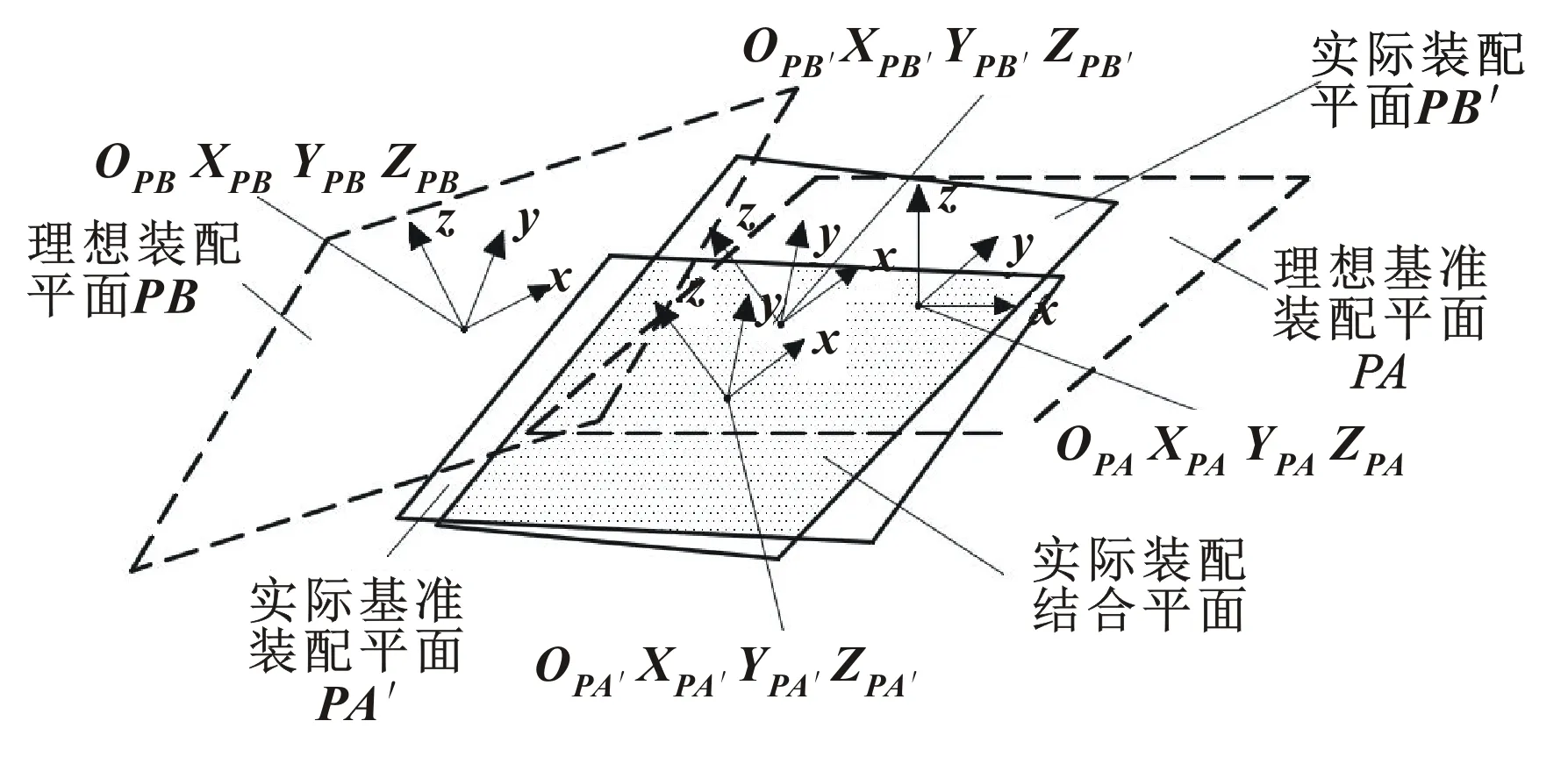
图4 装配结合面的位姿变化

设MAA′为平面PA到平面PA′的位姿误差变换矩阵，MA′B′为平面PA′到平面PB′的位姿误差变换矩阵，MB′B为平面PB到平面PB′的位姿误差变换矩阵。假设平面度是装配平面的主要公差项，则MAA′、MB′B可写作：

(3)

在理想状态下，实际装配基准面PA′完全贴合实际装配平面PB′，则可视为MA′B′=I。从刚体运动齐次变换原理可知，理想装配平面PB相对于理想基准装配平面PA的位姿误差变换矩阵，即为装配平面的结合面误差模型，可表示为

(4)

1.3 装配精度模型

装配体的误差传递过程与刚体运动的齐次变换类似，因此可通过类似于运动副的齐次变换原理，计算出机床整体的总装配误差。首先，建立零部件各结合面的误差模型；然后，依据装配拓扑结构中参与装配的顺序依次编号；最后，建立从基准装配零件到最终装配零件的几何误差传递模型，也称为装配精度模型。图5所示为n个零件以平面结合面的形式装配的装配误差传递关系。

图5 装配体几何误差传递示意

以零件Pn右侧平面为精度输出平面，零件P1左侧为基准装配平面，精度输出平面相对于基准装配平面的位姿误差变换矩阵Mall为

Mall=E1·M1,12·E12·M2,12·E23·…·

Mi,12·…·Mn,12·En

(5)

式中：E1为基准装配平面与零件P1的结合面位姿变换矩阵；Eij为零件Pi与零件Pj的结合面位姿变换矩阵；En为精度输出平面的误差变换矩阵；M1,12、M2,12、M3,12、Mi,12、Mn,12分别为理想状态下，在零件P1到零件Pn的装配方向上，实际装配平面相对于理想装配平面的位姿变换矩阵。

理想状态下，精度输出平面相对于基准装配平面的位姿误差矩阵M0可表示为

M0=M1,12·M2,12·…·Mi,12·…·Mn,12

(6)

则装配体的几何误差传递矩阵，也称为装配精度模型，可表示为

Eall=Mall-M0

(7)

1.4 装配精度公差优化分配模型

公差优化分配是在保证产品精度要求的前提下，通过选用适当的优化准则和约束条件，实现公差的优化分配[14]。在实现装配体精度优化设计时，将零部件结合面包含的公差作为优化变量，优化目标为满足精度要求下的最小加工成本，约束条件为装配体末端输出精度可靠度与公差选用原则。

(1)公差-成本数学模型。公差-成本模型[11]采用倒数平方模型，假设机床零部件尺寸链由n个待决定公差组成，则总成本C可表示为

(8)

(2)装配体末端输出精度可靠性约束。将装配体末端输出精度可靠度也看做是公差的函数，可用Ri(T)表示。假设装配体末端输出精度需满足的可靠度为ri，则装配体末端输出精度可靠度约束不等式可表示为ri-Ri(T)≤0，i=1,2,…,m。

(3)与公差原则相关的约束。对于同一功能要素，按照公差设计的重要程度，尺寸公差TD>位置公差TP>形状公差TS。

综合可得装配体装配精度的公差优化模型：

(9)

通过求解装配精度的公差优化模型，可在满足装配精度可靠性和公差设计原则的前提下，实现公差优化设计和成本控制[15]，并采用顶尖装配体验证所提方法的有效性。

2 顶尖装配体的公差建模与静态精度设计实例

图6 顶尖装配体结构及其零件图

图6中，a为圆柱面A的理想轴线，b为圆柱面B的理想轴线。平面C、D共同构成平面结合面S1；圆柱面A、B共同构成圆柱结合面S2。分别在平面C、D和轴线a、b上设置参考坐标系O1、O2、O3、O4，轴的位姿取决于实际结合面轴线的位姿[11]。顶尖装配体的结合面及所含公差项如表1所示。

表1 顶尖装配体结合面公差项

2.1 建立装配精度模型与精度可靠性状态函数

假定平面C为基准装配平面，C′为实际装配平面，C与C′的位姿误差变换矩阵为ECC′；平面D为基准装配平面，D′为实际装配平面，D与D′的位姿误差变换矩阵为EDD′；a′为圆柱面A的实际轴线，a与a′的位姿误差变换矩阵为Eaa′；b′为圆柱面B的实际轴线，b与b′的位姿误差变换矩阵为Ebb′；b与C的位置变换矩阵为MCb；顶尖顶点P与理想轴线a的位置变换矩阵为MaP，可写作：

平面C、D在装配过程中会定位，孔和轴过盈配合，所以实际变动平面C′和D′、实际轴线a′和b′均可视为完全重合。由式(6)—(18)可知，顶尖装配体精度模型可表示为

(10)

(11)

2.2 旋量参数与实际变动区间带宽的响应模型求解

利用蒙特卡洛模拟法分别建立顶尖装配体平面的位姿误差变换矩阵EDD′、EC′C中各SDT参数的响应面函数，和圆柱面结合面的位姿误差变换矩阵Ebb′、Ea′a中各SDT参数的响应面函数，分别写作

(12)

(13)

2.3 确定公差优化模型

顶尖装配体包含4个平面特征的尺寸公差和形状公差(t1、t2、t3、t4)，2个内孔特征的尺寸公差及位置公差(t5、t6)，1个轴特征的尺寸公差(t7)和直线度公差(t8)。由文献[12]中不同加工特征的公差-成本模型和零部件公差制造总成本模型，设定成本系数λ=15，则顶尖装配体的成本目标函数可表示为

(14)

顶尖装配体公差优化模型为

(15)

2.4 结果分析

在MATLAB运行环境中使用模拟退火遗传算法求解式(15)，得到如表2所示的公差优化值。因孔、轴的公差均为标准值，故按《机械设计手册》修正公差优化值，以《机械设计手册》中与公差优化值最相近的公差值作为顶尖装配体的最佳公差值。

表2 顶尖装配体公差优化结果

为验证公差优化的效果，分别给出公差初始值、公差优化值对应的装配精度可靠度和加工成本。可以看出：优化后的装配体加工成本为414.58元，相较于优化前装配体加工成本下降9.02%，装配精度可靠性提高到97.81%。由此可知：顶尖装配体的初始公差设计不能满足装配精度要求，需要进行公差优化，采用文中提出的精度设计方法可在保证装配精度可靠性的前提下，实现公差优化和加工成本控制。

3 结论

基于SDT公差建模和蒙特卡洛模拟的装配体公差优化设计方法，能够解决现有精度设计方法无法直接指导公差设计的问题。通过分析装配体装配误差累计传播路径上的公差变动、结合面误差和装配误差之间的关系，建立了SDT公差模型、结合面误差模型和装配精度模型，从而进一步建立了结合面公差与装配精度的映射模型。另外，结合公差制造成本和公差设计原则，建立了装配精度公差优化模型。利用所提方法对顶尖装配重要结合面公差进行优化设计，在满足装配精度可靠性的前提下，可使其加工成本降低9.02%，装配精度可靠性提高到97.81%，验证了该方法的有效性。