巧用“r2”求圆或圆内组合图形的面积

林贺密

为了帮助学生探索以圆半径为边长的正方形面积和圆面积的联系，巧用“r²”求圆和圆内组合图形的面积，可设计如下教学活动。

一、借助基本图形，探明基本规律

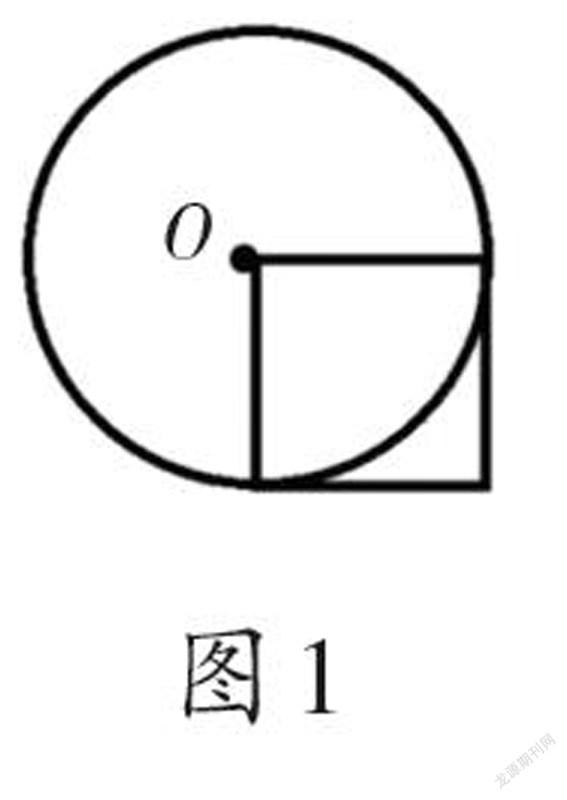
教师出示任务：如图1，已知正方形的面积是40cm²，你能求圆的面积吗？

学生独立完成，再重点讨论：“圆的半径是多少？怎样求圓的面积？”教师引导学生发现这个组合图形是由正方形和圆组成，因为正方形的边长ɑ=圆的半径r，S_正方形=ɑ²=r²=40（cm²），所以S_圆=πr²=40π（cm²）。小结：S_圆=S_正方形×π。

二、巧用转化思想，沟通解决方法

1.教师出示任务。图2～图4如果每幅图中阴影部分面积都是40cm²，那么请求出图2、图3中整圆的面积和图4中半圆的面积。并引导学生思考：“与图1相比，这3幅图发生了怎样的变化？阴影部分的图形和圆有什么联系？怎么求圆或半圆的面积？”

2.转化图形。学生独立尝试后小组交流，选派学生代表上台汇报。

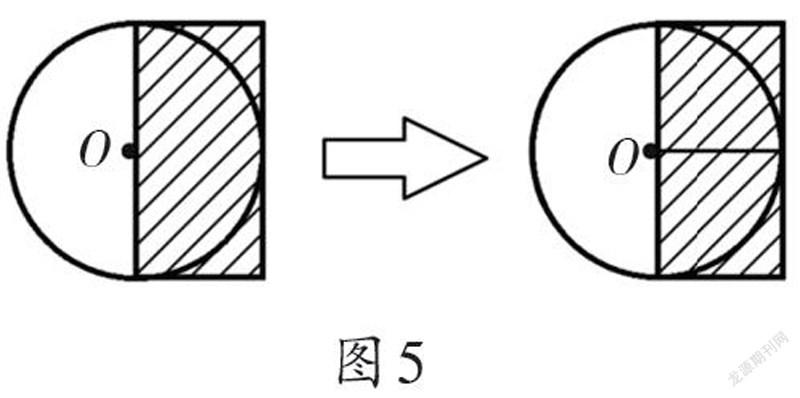
预设：（1）对折法。通过对折，可把长方形平均分成两个小正方形（如图5），正方形的边长ɑ=圆的半径r；小正方形的面积为长方形面积的一半；S_正方形=ɑ²=r²=40÷2=20（cm²）。得出：S_圆=S_正方形×π=20π（cm²）。

（2）轴对称法。以图3中线段AB为对称轴画三角形OAB的轴对称图形O′AB，由此得到正方形OAO′B，它绕点O旋转45°后，与基本图形形状一致（如图6）。三角形OAB的面积为正方形OAO′B面积的一半。根据基本图形正方形的边长ɑ=圆的半径r；S_正方形=ɑ²=r²=40×2=80（cm²），得出：S_圆=S_正方形×π=80π（cm²）。

（3）分割旋转法。将图4中三角形ABC沿半径OB分割，分割后的图形经旋转得到基本图形（如图7），S_三角形=S_正方形=r²=40（cm²），得出：S_半圆=S_正方形×π÷2=20π（cm²）。

3.沟通联系。教师引导学生进行比较：“这三道题有什么相同点和不同点？你有什么发现？”

预设：学生通过比较发现，三个图形都能转化为基本图形（如图1）。这些图形都无法通过直接求r值来计算圆的面积。这时，可以利用对称、旋转等方法将复杂图形变为基本图形，直接用“r²”的值来求圆或半圆的面积。

三、适当变式拓展，明晰解题模型

教师出示练习题：图8中，已知平行四边形ABCD的面积是50cm²，求阴影部分的面积。

学生尝试解决后，进行全班交流。教学反馈：在图8中，从D点出发作线段AB的垂线，得到的正方形的面积等于平行四边形面积的一半（如图9），即正方形EBOD的面积是25cm²，则圆的面积为25πcm²，而阴影部分面积为圆面积的1/4，即25/4πcm²。

以上教学，学生把以圆的半径为边长的正方形作为基本图形，探索圆面积与正方形面积之间的关系，并运用对称、分割、旋转等方法，总结出了用“r2”求圆内有关组合图形面积的方法，发展了空间观念和推理能力。

（浙江省宁波市海曙外国语学校   315175）