电缆硅橡胶附件温度和热老化对接头界面压力的影响

杜光旭，方春华，夏 荣，丁 璨，吴 田

（1. 三峡大学 电气与新能源学院，湖北 宜昌 443002；2. 中国电力科学研究院有限公司，湖北 武汉 430074）

0 引言

电缆接头是电缆事故发生的薄弱环节，电缆附件与交联聚乙烯界面压力不足是引发接头绝缘击穿故障的重要原因之一。已有研究表明，电缆附件与主绝缘界面压力在0.10～0.25 MPa 时，能够满足电气强度的要求[1-2]。电缆线芯发热会导致附件绝缘材料温度升高，影响附件硅橡胶材料的力学性能，同时附件长时间在高温下运行会导致附件硅橡胶老化，力学性能出现衰退[3-4]。因此，研究电缆附件温升和老化后的界面压力具有重要意义。

目前，国内外对电缆附件界面压力影响因素开展了许多研究。柳松等[5]对电缆附件的过盈配合进行ANSYS 仿真，研究了过盈量、厚度和面压的关系；谢强等[6]通过建立电缆接头仿真模型，研究了橡胶本构模型和附件结构对接头界面压力的影响；包淑珍等[7]研究了退役电缆绝缘层在变温环境中的弹性模量与界面压力的关系，但附件在变温和老化环境中的力学性能缺少研究；柳松等[8]通过测量不同温度下附件的弹性模量计算界面压力，但该方法存在一定误差，采用橡胶本构模型计算界面压力更能体现材料的非线性力学性能。鲁中亚等[9]研究了预制型电缆终端应力锥在变温环境下的应力应变关系，拟合出Mooney-Rivlin 本构模型参数，但没有对高温环境中的界面压力变化进行研究。

综上所述，现有研究主要集中在电缆附件常温环境下的界面压力，缺乏高温环境下和老化后附件硅橡胶材料的拉伸应力应变数据和本构模型参数，对变温环境中电缆接头界面压力变化的研究也较少。为此，本文以10 kV 冷缩电缆中间接头为例，采用单轴拉伸试验测定附件硅橡胶材料在高温环境和不同热老化时长后的应力应变数据，根据试验数据拟合硅橡胶的超弹性Yeoh本构模型，建立简化的中间接头二维轴对称有限元模型，利用仿真分析温度及热老化对附件硅橡胶界面压力的影响。

1 电缆接头附件拉伸试验

1.1 试验制作及试验工况

按照HG/T 2645—2011《橡胶专用裁刀技术条件》，将高温硫化形成的半导电硅橡胶和绝缘硅橡胶裁剪成哑铃Ⅱ型试样，如图1 所示。试样的窄部分平均宽度为4 mm，平均厚度为2 mm，试样标距为25 mm，试样平均长度为75 mm。

图1 哑铃型硅橡胶试样Fig.1 Dumbbell-shaped silicone rubber specimens

由于三芯电缆附件外部是由铠装带绕包而成，接头内部环境密闭，对流换热系数小，导致附件外表面和内表面温差小于7℃[10]，故本文在计算界面压力时认为附件各处温度相等。为了提高试验准确性，模拟电缆附件所处环境温度，硅橡胶试样在常温25℃，高温50、75、100℃进行拉伸试验，每组拉伸试验重复3次。

按照GB/T 3512—2001，采用上海一恒科学仪器有限公司生产的DHG-9425A 型鼓风干燥箱在130、150、170℃对试样进行加速热老化试验。因为10 kV 电缆接头产生的位移形变为1～2 mm，附件厚度为10～20 mm，位移变形约为附件厚度的10%，所以老化时将哑铃型试样预拉伸10%。老化完成后，取出试样，室温下放置30 min 后进行拉伸。依据GB/T 528—2009[11]，采用馥勒仪器科技有限公司生产的FL-GD 型拉伸试验机进行单轴拉伸试验，拉伸速率为500 mm/min。

1.2 拉伸应力应变曲线

图2、图3分别为附件绝缘硅橡胶和半导电硅橡胶在不同温度下的应力应变曲线。从图2～3 可以看出，绝缘硅橡胶和半导电硅橡胶的力学性能受温度影响较大，对温度比较敏感。在相同伸长率下，两种材料在常温25℃时的应力最小，随着温度升高，绝缘硅橡胶和半导电硅橡胶的拉伸应力呈先增大后减小的趋势，在75℃时拉伸应力最大。附件硅橡胶拉伸变形时，分子链变成伸展状态，有序度增加，熵变小，由于分子热运动，分子会自发地恢复到原来状态，使熵增大，由此产生弹性恢复力。当温度升高时，使熵恢复趋势更加强烈，因此温度升高，弹性模量会随之增加。当温度高于75℃，考虑到热效应和体积膨胀，同时温度过高使有效交联密度降低，导致分子间作用和链段间作用削弱，应力会减小。

图2 不同温度下绝缘硅橡胶的应力应变曲线Fig.2 Stress-strain curves of insulating silicone rubber under different temperatures

图3 不同温度下半导电硅橡胶的应力应变曲线Fig.3 Stress-strain curves of semi-conductive silicone rubber under different temperatures

由于在130、150、170℃热老化条件下硅橡胶的应力应变曲线变化趋势相同，只列出绝缘硅橡胶和半导电硅橡胶在130℃热老化48、96、144、192、360、528、720 h 时测量得到的应力应变曲线，结果如图4～5所示。由图4～5可以看出，随老化时间的增加，在相同伸长率下，拉伸应力不断下降，力学性能降低。两种材料的应力应变响应均为非线性弹性特征，随着材料温度升高和老化时间增加，这种非线性特征的趋势没有发生改变。

图4 130℃不同老化时长绝缘硅橡胶的老化应力应变曲线Fig.4 Stress-strain curves of insulating silicone rubber after ageing for different time at 130℃

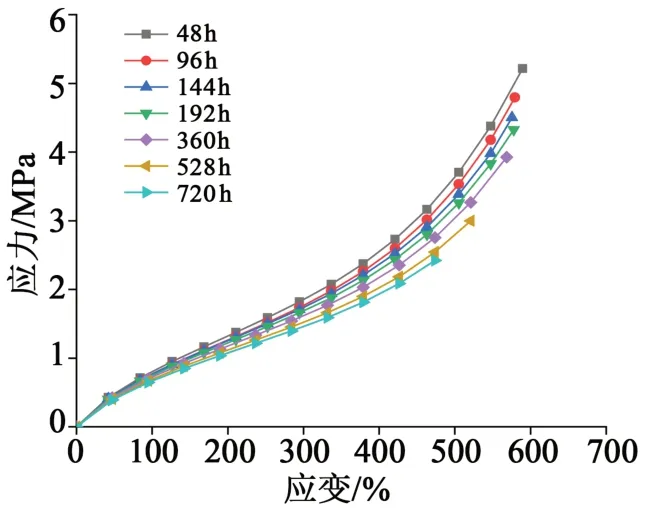
图5 130℃不同老化时长半导电硅橡胶的应力应变曲线Fig.5 Stress-strain curves of semi-conductive silicone rubber after ageing for different time at 130℃

2 界面压力仿真分析

2.1 仿真模型

以10 kV 冷缩型电缆中间接头为研究对象，建立二维轴对称接头模型，其仿真模型结构如图6 所示。为减少计算量，简化后的电缆接头模型由铜芯、交联聚乙烯、应力锥、高压屏蔽管、电缆附件绝缘、绝缘胶带、压接管组成。应力锥和高压屏蔽管由半导电硅橡胶组成，附件绝缘由绝缘硅橡胶组成。应力锥、高压屏蔽管和绝缘橡胶通过高温硫化成附件整体。电缆冷缩附件与电缆主绝缘XLPE 冷装配，形成不同介质复合界面，附件硅橡胶以一定的过盈量压缩变形在复合界面产生压力。

图6 10 kV电缆接头仿真模型结构示意Fig.6 Schematic structure of 10 kV cable joint simulation model

在有限元仿真分析中，采用罚函数分析方法来解决硅橡胶的几何非线性问题。当两个边界相互挤压时，在两接触面的各节点间建立一个虚拟单元模拟面与面接触。对模型定义装配体，创建接触对，设置硅橡胶为接触体，交联聚乙烯为目标体，接触表面从几何目标表面偏移的量即为过盈量。模型两端边界设置为辊支承约束条件。在二维模型网格划分中，研究的是硅橡胶在过盈面的变形及受力，故硅橡胶划分较细，交联聚乙烯及铜芯模型中网格较少。电缆中间接头附件的硅橡胶材料在压缩变形过程中体积变化很小，通常被视为近似不可压缩和各向同性的超弹性材料，变化过程复杂且高度非线性，因此本文基于橡胶超弹性Yeoh 本构模型，利用与材料应变能偏量部分有关的3个材料参数C10、C20和C30来计算界面压力。

2.2 应力-应变关系确定硅橡胶本构模型

Yeoh 本构模型的弹性应变能函数关系如式（1）所示[12]。

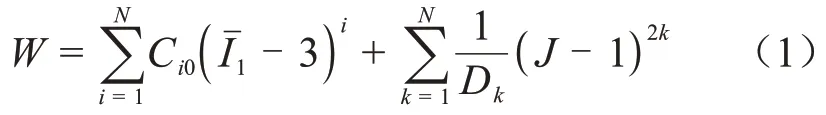
式（1）中：J为硅橡胶变形前后的体积比；Iˉ1为第一应变张量不变量；N、Ci0和Dk为输入参数。由于硅橡胶近似为不可压缩材料，取J=1。实际应用中，取N=3，代入式（1）得到式（2）。

式（2）中：W为应变能密度；I1为第一格林应变不变量；C10、C20、C30为Revlin 系数，其中C10为小应变时的初始剪切模量，在小应变时，橡胶填料网格没有被破坏，只有C10初始剪切模量起作用；负值的C20体现中等变形时材料的软化过程；正值的C30体现大变形时材料的硬化。

Yeoh 本构模型拟合精度高，拟合曲线与硅橡胶单轴拉伸力学行为符合。本文利用试验得到的应力应变数据，将数据导入COMSOL 软件中，然后拟合出材料本构模型常数，得到常温25℃，高温50、75、100℃温度下绝缘硅橡胶和半导电硅橡胶的本构模型参数分别如表1、表2 所示，可以看出绝缘硅橡胶和半导电硅橡胶在75℃时的初始剪切模量最大。在130℃下老化48、96、144、192、360、528、720 h 的绝缘硅橡胶和半导电硅橡胶拟合本构模型参数分别如表3、表4 所示，可以看出，随老化时间增加，初始剪切模量C10不断减小。

表1 不同温度下绝缘硅橡胶Yeoh模型参数Tab.1 Fitting results based on Yeoh model for insulating silicone rubber at different temperatures

表2 不同温度下半导电硅橡胶Yeoh模型参数Tab.2 Fitting results based on Yeoh model for semi-conductive silicone rubber at different temperatures

表3 130℃老化下绝缘硅橡胶Yeoh模型参数Tab.3 Fitting results based on Yeoh model for insulating silicone rubber after ageing at 130℃

表4 130℃老化下半导电硅橡胶Yeoh模型参数Tab.4 Fitting results based on Yeoh model for semi-conductive silicone rubber after ageing at 130℃

2.3 界面压力理论计算

橡胶本构关系由应变能密度函数定义，如式（3）所示[13-14]。

式（3）中：σ′为Cauchy 应力偏量；DEV[▪]表示张量[▪]的偏量；W为变压缩前单位体积的应变能密度函数；1与2为应变第一与第二不变量；J是硅橡胶变形前、后的体积比；左Canchy-Green 张量B=F∙FT，F为硅橡胶的变形梯度张量。

轴对称平面应变的3个主伸长量λi(i=r, θ, z)如

式（4）所示。

式（4）中：R为硅橡胶变形前的半径；r为硅橡胶变形后的半径。结合式（3），计算可得式（5）。

式（5）中：σr为径向应力；σθ为环向应力。

半导电材料受压平衡方程为式（6）。

联立式（2）、式（5）和式（6），可得式（7）。

考虑橡胶近似不可压缩，可得式（8）。

式（8）中：ub表示半导电层在Rb处受到的径向变形；R1、r1表示绝缘硅橡胶变形前、后的半径。

对于绝缘层，绝缘硅橡胶外表面径向应力为0，联立式（7）和式（8）可以计算得到绝缘层内径为Rb处的径向应力（Pb）表达式，如式（9）所示，其中Ra为接头外径。

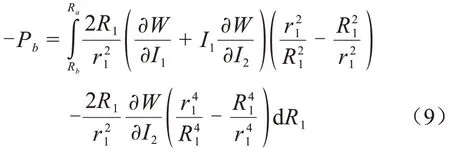
对于半导电层，以Pc和uc分别表示半导电硅橡胶在Rc处的径向应力和发生的径向变形，R2、r2表示半导电硅橡胶变形前、后的半径，则有式（10）。

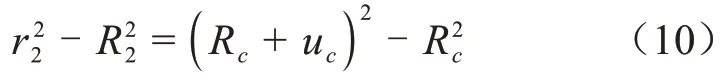
根据式（7）和式（10）可以计算得到电缆接头内径处的径向应力表达式，如式（11）所示。

以uc′表示电缆层在Rc处发生的变形，则由纵向应力和接触界面变形连续性，可得式（12）；电缆层在Rc处径向应力为Pc，Ec为XLPE 的弹性模量，vc为XLPE的泊松比。过盈配合界面变形关系为式（13）。

由半导电层橡胶的近似不可压缩性可得式（14）。

联立式（9）～（14）可解出电缆接头与电缆绝缘XLPE 间的界面压力以及电缆绝缘XLPE 的径向应力及变形。

2.4 界面压力分布规律

为了研究电缆中间接头界面压力分布规律，将25、50、75、100℃温度下的附件硅橡胶本构模型参数代入仿真模型，取过盈量为1.5 mm，得到电缆接头应力云图如图7所示，应力锥截面、绝缘硅橡胶截面径向应力分布和位移形变图如图8所示。

图7 电缆接头应力分布云图Fig.7 Stress distribution map of cable joints

图8 应力分布和位移场Fig.8 Stress distribution and displacement field

分析图7～8 得到：电缆接头为轴对称结构，中间接头界面压力对称分布，相同半径圆周上的应力大小相等。附件最大形变出现在附件与交联聚乙烯XLPE 过盈配合处，其特点是位移形变从接头内侧到外侧逐渐减小；附件最大应力出现在附件与交联聚乙烯XLPE 接触面，其特点是应力从接头内侧到外侧逐渐减小。

图9为绝缘硅橡胶和半导电硅橡胶根部界面压力与过盈量的关系图。从图9 可以看出，界面压力随过盈量线性增加，过盈量每增加0.5 mm，绝缘硅橡胶根部界面压力增加0.045 5 MPa，半导电绝缘硅橡胶根部界面压力增加0.057 7 MPa。

图9 界面压力与过盈量Fig.9 Interfacial pressure and interference volume

为了更直观地研究电缆接头轴向界面压力大小，定义接头应力锥左端为原点，向右为正方向，沿接头复合界面采集轴向的压力数据，得到接头界面压力分布如图10所示。

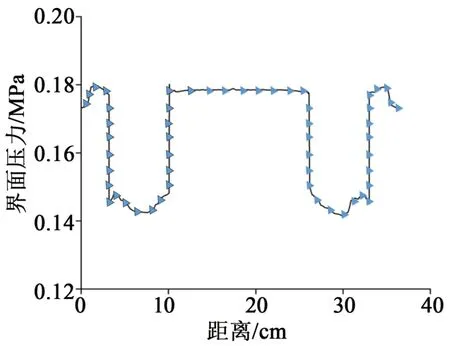
图10 电缆接头轴向界面压力分布Fig.10 Pressure distribution at the axial interface of cable joints

10 kV 电缆冷缩附件两端为应力锥结构，应力锥界面压力由半导电硅橡胶压缩形变产生，由图10可知，附件外端口压力为0.173 MPa，在1.1 cm 处上升到0.180 MPa，在3.2 cm 处，界面压力显著下降到0.146 MPa。这是因为应力锥厚度减小，绝缘硅橡胶厚度增加，绝缘硅橡胶弹性模量小于应力锥硅橡胶模量，弹性模量对力学性能的计算影响较大。绝缘硅橡胶根部最小界面压力为0.143 MPa，在10.1 cm处，附件内侧材料为高压屏蔽管，压力显著上升到0.179 MPa。由于电缆中间接头为轴对称结构，故两端压力变化趋势一样。

针对电缆接头的薄弱点，对接头绝缘与XLPE接触面、应力锥根部与XLPE 接触面及高压屏蔽管与XLPE 接触面的界面压力展开理论求解和有限元数值仿真计算，对比理论求解和有限元数值仿真计算结果，结果如表5 所示。从表5 可以看出，理论计算与仿真结果差异较小，偏差在2%以内，二者的吻合度高。

表5 电缆接头复合界面压力的计算结果Tab.5 Calculation results of composite interface pressure for cable joints

3 附件高温对界面压力的影响

为研究不同温度下界面压力对电缆XLPE 形变的影响，设10 kV 电缆铜芯为刚体，电缆铜芯直径为15 mm，绝缘厚度为6 mm。根据文献[7]测量的交联聚乙烯弹性模量随温度变化的数值，计算得到XLPE径向位移量随压力的变化关系，如图11所示。

从图11可以看出，在界面压力作用下，XLPE发生一定的径向位移，当温度升高时，XLPE 的弹性模量降低，径向位移量增大。当界面压力为0.2 MPa时，XLPE在20℃的形变量为2.3 μm，在80℃的形变量为12 μm，形变率分别约为0.15%和0.80%。温度升高，电缆XLPE的压缩形变可忽略。

图11 不同界面压力下的XLPE径向位移Fig.11 Radial displacement of XLPE at different interface pressures

为了研究温度对电缆中间接头界面压力的影响，将50、75、100℃温度下的附件硅橡胶本构模型参数代入仿真模型，计算得到过盈量为1.5 mm时不同温度下电缆接头的应力分布云如图12所示，可以看出在75℃时，界面压力最大。

图12 不同温度下接头应力分布云图Fig.12 Stress distribution maps of cable joints at different temperatures

过盈量为1.5 mm 和2.0 mm 时，应力锥和绝缘硅橡胶根部界面压力随温度的变化关系如图13 所示。从图13 可见，温度为50、75、100℃时绝缘硅橡胶根部界面压力增加了9.1%、12.3%、6.4%，半导电硅橡胶根部界面压力增加了9.2%、16.3%、5.6%，电缆接头在75℃时界面压力最大。电缆附件硅橡胶为柔顺大分子链段组成的高聚物，大分子链在外力拉伸作用下构象发生改变产生高弹性。由于大分子链段对温度有很强的依赖性，根据交联橡胶弹性体的弹性模量公式可知弹性模量大小与温度和弹性体有效交联密度成比例关系[15-19]。当绝缘硅橡胶和半导电硅橡胶在25～75℃时，随温度升高，弹性模量增加，此时构象熵增加占主导因数。当绝缘硅橡胶和半导电硅橡胶在75～100℃时，随温度升高，体积发生膨胀，分子链间的自由空间加大，分子链的热运动活性变高，运动加剧，有效交联密度降低，导致分子间作用和链段间作用削弱，宏观表现为橡胶弹性模量降低，说明当硅橡胶温度超过75℃时，有效交联密度对橡胶弹性模量起主要贡献作用。

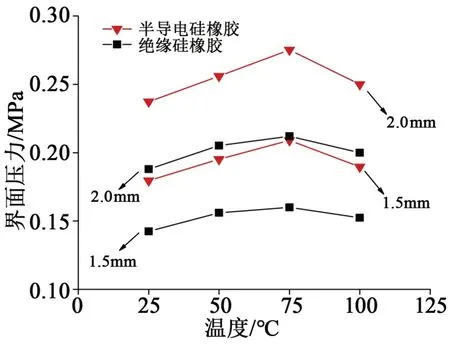
图13 不同温度下硅橡胶根部界面压力Fig.13 Interfacial pressure at the root of silicone rubber at different temperatures

4 附件老化对界面压力的影响

4.1 界面压力下降程度

电缆附件在与电缆本体过盈配合时，硅橡胶压缩产生形变，在硅橡胶单位体积内储存应变能。为研究热老化对应力集中单元处应变能密度的影响，选取130℃热老化的数据计算，结果如图14所示。

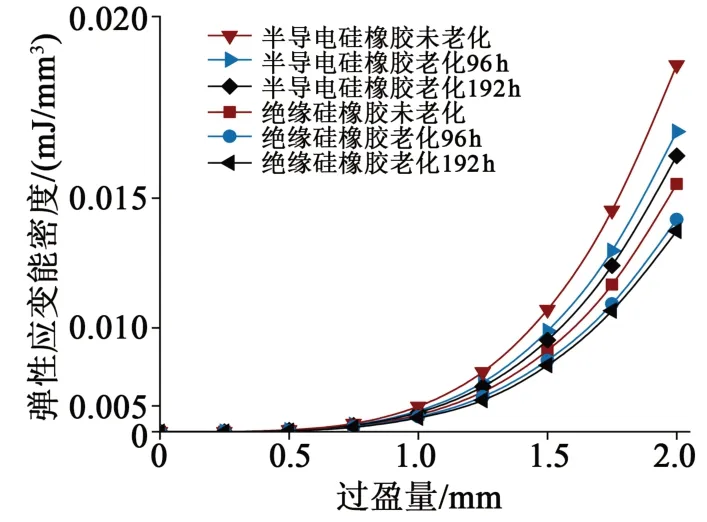
图14 不同老化时长硅橡胶弹性应变能密度曲线Fig.14 Elastic strain energy density curves of silicone rubber with different ageing time

从图14可以看出，两种硅橡胶的弹性应变能密度随过盈量的增加而增加。在相同过盈量下，半导电硅橡胶的弹性应变能密度大于绝缘硅橡胶的弹性应变能密度。老化后，两种硅橡胶的应变能密度都减小，在老化192 h，过盈量为2.0 mm 时，半导电硅橡胶的应变能密度减小了13.3%，绝缘硅橡胶的弹性应变能密度减小了10.0%。随老化时间增加，应变能密度函数斜率变小，反映硅橡胶单位体积积蓄的能量减少，硅橡胶的力学性能降低，从而产生的界面压力减小。

为研究电缆附件热老化后的界面压力变化，通过热老化实验获得在130、150、170℃温度下老化48、96、192、360、528、720 h 的半导电硅橡胶应力应变曲线，计算在相同过盈量下各老化时间节点的界面压力下降程度，结果如图15 所示。从图15 可以看出，在相同过盈量条件下，随着老化时间的增加，电缆附件界面压力减小，且随着老化的进行呈现出先快后慢的变化规律，在130℃下老化192 h，应力锥根部界面压力下降了13.6%；而在相同老化时间内，热老化温度为150℃时，根部界面压力下降了24.5%。通过对比不同热老化温度下的界面压力变化率可以看出，温度对热老化速率至关重要，热老化温度越高，硅橡胶根部界面压力受到的影响越明显。

图15 界面压力下降程度随老化时间的变化曲线Fig.15 Curves of the decrease degree in interfacial pressure with ageing time

由于硅橡胶试样在热老化初期发生了交联反应，使得硅橡胶内部形成了更加紧密的网格结构，而交联度的增加会抑制聚合物链间的滑动，降低聚合物的柔顺性，破坏硅橡胶原有的高弹性，从而导致绝缘硅橡胶的根部界面压力降低。当绝缘硅橡胶受到长时间高温的作用时，分子链的运动加剧，当超过化学键的离解能时，就会引起高分子链的热降解，且随着老化时间的增加，热降解反应逐渐占据主导地位，造成硅橡胶材料大分子链断裂严重，导致其力学性能下降，最终使硅橡胶弹性减小，甚至失去弹性[20-22]。

4.2 老化预测模型

硅橡胶的老化性能降低率又被称为老化程度（P），在本研究中采用老化前后硅橡胶根部界面压力的下降程度表示。

在一定温度T下老化，橡胶形变产生的界面压力随时间减小，采用文献[23]提出的修正公式对界面压力下降程度P和老化时间t进行拟合，如式（15）所示。

式（15）中：P为任意时刻t的界面压力Pt与初始压力P0的比值；α为与T无关的常数；k为与T有关的速度常数。在一定温度下，速率常数k与老化温度T之间的关系服从Arrhenius公式，如式（16）所示。

式（16）中：A为碰撞因子；E为表观活化能；R为气体常数；T为老化温度。采用逐次逼近的方法求解待定参数，逼近准则为使式（17）中I值最小。

式（17）中：I为逼近准则；pij为第i个温度下第j个测试点性能的试验值；̂ij为第i个老化温度下第j个试验点性能的计算值。通过计算得到在α=0.43 时，I值最小。

根据式（15）拟合lnP和tα的直线关系式，得到各温度下的速率常数，分别为k130=0.053，k150=0.114，k170=0.219。对式（16）进行对数变换，将速率常数公式变换为式（18）的直线关系式，将k130、k150、k170值取对数，对lgk和T-1进行线性拟合。

式（18）中，Y=lgk，C=lgA，D=E/(2.303R)，Z=T-1。运用最小二乘法计算线性方程的系数C和D，利用r检验计算线性相关系数，相关系数r的值都大于0.95，说明相关性显著，预测值可信。得到速率常数k与老化温度T的关系式为式（19）。

综上，得到老化预测模型如式（20）所示。

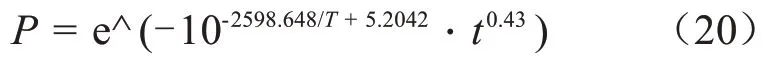
已知冷缩附件的最小初始界面压力为0.18 MPa，电缆运行的最高温度为90℃（363 K），满足电气要求的最小界面压力为0.1 MPa，因此界面压力应保持在P大于0.55 以上，结果如图16 所示，使用寿命约为28.9年。

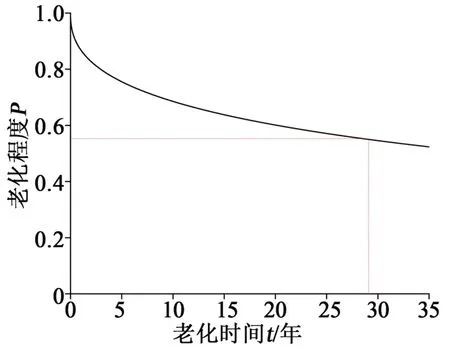
图16 90℃下老化程度随老化时间的变化曲线Fig.16 Ageing degree at 90℃changes with ageing time

5 结论

（1）电缆附件最大位移形变出现在附件与交联聚乙烯过盈配合处，且从附件内侧到外侧位移形变逐渐减小；附件最大应力出现在与交联聚乙烯接触面上，且从附件内侧到外侧应力逐渐减小。

（2）温度对附件硅橡胶材料的影响较大，随温度升高，两种材料出现了力学性能改变，通过建立有限元仿真模型分析不同温度和不同老化时间点的界面压力变化，在相同过盈量下，与常温相比，温度为50、75、100℃时绝缘硅橡胶根部界面压力增加了9.1%、12.3%、6.4%，半导电硅橡胶根部界面压力增加了9.2%、16.3%、5.6%，电缆接头在75℃时界面压力最大。

（3）附件硅橡胶材料的初始剪切模量随老化时间的增加而减小，在复合界面水平路径上，相同节点处，老化前的界面压力和弹性应变能密度均大于老化后，且界面压力下降程度随着老化的进行呈现出先快后慢的变化规律。建立了半导电硅橡胶使用寿命的预测模型，通过预测模型计算，当附件使用温度为90℃、界面压力大于初始界面压力55%时，使用寿命为28.9年。