振动诱发金属微粒弹跳对圆盘绝缘子表面电荷积聚的影响

2022-12-27王文渠赵慧存苑晓晨

绝缘材料 2022年11期

王文渠，高宇，赵慧存，苑晓晨，王欢

（天津大学电气自动化与信息工程学院，天津 300072）

0 引言

气体绝缘开关设备（gas insulated switchgear，GIS）与气体绝缘输电线路（gas insulated transmis‐sion line，GIL）在大容量、长距离电能输送与区域联网工程建设中应用日益广泛，这归功于其占地面积小、传输损耗少、运行可靠性高、环境适应性强等优点[1]。GIS/GIL 因其良好的灵活性、适应性和互动性，成为可代替架空线路、电力电缆、敞开式变电站等传统输变电方式的更优解决方案。但相比于交流气体绝缘设备的推广应用，直流领域中GIS/GIL的研发工作仍面临许多技术问题。

目前普遍认为，GIS/GIL 中绝缘子表面电荷的积聚是制约其在直流电压作用下绝缘性能的关键因素。此外，在GIS/GIL 的安装和长期运行过程中引入的金属微粒对表面电荷的积聚也有促进作用。金属微粒会引起电场的严重畸变，在绝缘子附近诱发微放电，引起绝缘表面电荷密度的激增[2-3]，甚至导致绝缘失效。在GIS/GIL 的运行过程中，高压断路器或隔离开关动作形成的强烈冲击、短路故障、外部撞击等因素均会导致设备发生机械振动[4-6]。振动不仅会导致设备内部元件磨损，材料变形，还会造成绝缘材料的加速劣化和气室泄漏[7]，同时有可能引起金属微粒弹跳运动，影响表面电荷的积聚特性，威胁设备的绝缘安全。为提高直流GIS/GIL的运行可靠性，有必要针对振动诱发金属微粒弹跳对表面电荷积聚的影响开展系统性研究。

目前，国内外学者对金属微粒的动态行为和危害性给予了高度关注。研究发现，线形金属微粒的运动往往伴随着气体放电的现象[8]。S OKABE 等[9]研究了金属微粒在同轴电极模型中的运动行为，发现金属微粒在导体与外壳之间往复运动过程中会产生局部放电，其出现的频率与微粒往复运动的频率几乎相同。律方成等[10]采用仿真软件，基于楔形电极建立了电-力瞬态耦合模型，精确预测了金属微粒的运动轨迹，对比了不同直径与材料的金属微粒轨迹的差异，将球形金属微粒的运动分为3个阶段，并对金属微粒的污染问题提出了相关治理方法[11]。对于初始位置在外壳上的金属微粒，王健等[12]建立了同轴电极模型，在考虑金属微粒碰撞的随机性与SF6混合气体阻力的基础上研究了其运动规律。M M MORCOS 等[13]发现线形金属微粒由于其端部电场更加集中，易引起气体电离，从而对设备产生更大的危害。K SAKAI等[14-15]通过对比球形和线形微粒引发空气击穿时的位置，发现线形微粒引发气体击穿的时间更早。P WENGER 等[16]在同轴电极模型下采用高速摄像机观察了金属微粒的运动过程，归纳了金属微粒运动3种典型模式。综上所述，此前关于金属微粒的研究主要关注其在直流电场中的运动，而对实际工况中设备振动诱发的金属微粒弹跳及表面电荷积聚现象却鲜有报道。

本文以126 kV 圆盘绝缘子为试样，搭建非周期性振动发生装置，测量振动条件下线形金属微粒的运动轨迹及绝缘子表面电荷积聚情况，总结金属微粒在不同初始位置下受到振动后的运动模式，讨论启举方式和微粒最终位置对绝缘子表面电荷积聚的影响。

1 实验

1.1 实验样品

本实验采用的126 kV 圆盘绝缘子由山东泰开电器绝缘有限公司提供。为模拟真实GIS/GIL运行工况下绝缘子所处电场条件，设计了同轴圆柱电极结构，绝缘子及同轴圆柱电极实物如图1(a)所示。绝缘子以及电极的具体尺寸如图1(b)所示。环氧绝缘子表面从外部至中心分为3个区域，分别为：与地电极接触区（x=123～172.5 mm）、平面区（x=83～123 mm）以及非平面区（x=44～83 mm），其中非平面区从外部至中心分为3 段，分别为圆弧段A1、直线段L1 以及圆弧段A2。其中，A1 为非平面区和平面区的交界区。在GIS/GIL 中，线形和球形金属微粒最为典型。研究表明，线形金属微粒由于其端部电场更加集中，更容易引起电离，从而对设备的绝缘性能影响更大。线形微粒的长度大多在mm 量级，直径在100 μm量级[17-18]。故本实验所采用的铝制线形金属微粒长度为5 mm，截面半径为0.5 mm。

图1 绝缘子以及电极设置Fig.1 Spacer and electrode setting

1.2 实验平台设计

实验装置示意图如图2 所示，根据圆盘绝缘子轴对称的结构特点，设计了一套探头及绝缘子运动单元，主要由三组平移台和两组旋转台组成，可以测量得到绝缘子上表面的电位[19]。

为模拟GIS/GIL 受到的振动，设计了非周期振动发生装置，其在实验腔体中的位置如图2 所示。该装置放置于地电极的外侧，输出的最大加速度为338.9 m/s2，振动频率为1.1 Hz，实验前调整其高度使撞击点位于地电极中央。研究表明，GIS 中高压断路器动作或发生具有幅值高、阻尼强的操作过电压时，其产生的瞬时冲击引发的金属外壳振动的加速度在9.8×10-5～980 m/s2[20]。本文选取的加速度338.9 m/s2在此范围之内，振动加速度的时域曲线如图3所示。该振动装置通过无线继电器（型号为JYDAM0404D，北京聚英翱翔电子有限公司）与计算机进行通信，由上位机来控制振动装置的启动与停止。

图2 实验装置Fig.2 Experimental device

图3 绝缘子振动加速度时域曲线Fig.3 Time domain curve of insulator vibration acceleration

1.3 实验方法

实验前，在60℃下对圆盘绝缘子进行24 h 的干燥处理，保证无电荷残留后，将无水乙醇清洁过的线形金属微粒放置于初始位置。实验在空气氛围中进行，温度控制在（25±1）℃，相对湿度为（20±2）%。本文旨在揭示偶发振动诱导的金属微粒运动导致的表面电荷积聚机理，考虑到空气比SF6更易电离，一旦由于微粒畸变电场诱发微放电，可以更为清晰地观察到电荷积聚现象，从而为理解和揭示表面电荷积聚的机理提供便利条件。因此，采用空气作为介质进行实验，这种方法也被此前的研究人员所采用[21-23]。

为对比说明振动引起金属微粒跳动对表面电荷积聚的影响，分别开展了I 和II 两类实验。在第I类中，无金属微粒，电极间施加-30 kV 直流电压1 h后，测量表面电荷密度分布。在第II类中，施加电压后立刻启动振动发生装置，振动施加时间控制在5 s以内。采用高帧率摄像机记录金属微粒从开始运动到静止的全过程，加压1 h 后，测量表面电荷密度的分布。对比I、II两类实验结果中电荷积聚特征的差异，分析振动诱导金属微粒弹跳的影响。

2 实验结果

2.1 第I类实验的典型结果

当绝缘子与电极上均未放置金属微粒时，测得的表面电荷典型分布特征如图4 所示。由图4 可见，绝缘子非平面区（虚线内）的负极性表面电荷呈环状分布，正极性电荷主要积聚在平面区与非平面区的交界处。正、负极性电荷密度的最大值分别为0.3 pC/mm2和-0.2 pC/mm2。总体来说，表面电荷的积聚情况并不显著。

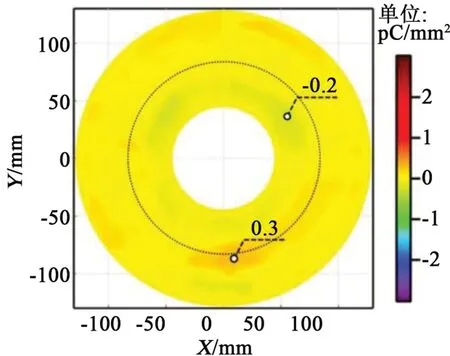
图4 第I类实验中表面电荷典型分布特征Fig.4 Surface charge distribution of group I

2.2 第II类实验的典型结果

在第II 类实验中，为了更为细致地研究振动对金属微粒弹跳和表面电荷积聚的影响，将金属微粒的初始位置分为绝缘子平面区、高压电极和地电极3种情况。当微粒初始位置在绝缘子平面区时，振动并未造成微粒产生位移，因此仅展示在有振动与无振动条件下，平面区存在金属微粒时的电荷积聚情况，如图5 所示。由图5(a)可见，未施加振动时，绝缘子非平面区被环形的负极性电荷覆盖，正极性电荷斑出现在交界处，最大正、负电荷密度分别为0.7 pC/mm2和-0.7 pC/mm2。由图5(b)可见，施加振动时，最大正、负电荷密度分别为0.8 pC/mm2和-0.7 pC/mm2。结果表明，初始位置位于平面区的金属微粒无论振动与否，均不会对电荷积聚特性产生明显影响。

图5 微粒初始位置在平面区的电荷测量结果Fig.5 Charge measurement results of particle initial position in plane region

当金属微粒的初始位置位于高压电极时，实验发现，振动诱发金属微粒离开电极的方式有两种，方式1：直接从起始静止位置启举；方式2：向电极边缘滚动一段距离后启举。

当微粒以方式1 离开高压电极时，经过多次碰撞停留在绝缘子平面区，如图6(a)所示，对应的表面电荷分布特性如图6(b)所示，最大正、负电荷密度分别为0.5 pC/mm2和-0.8 pC/mm2。可见，当微粒直接从高压电极飞出，最终停留在平面区时，对表面电荷积聚的影响较小。当微粒以方式2离开高压电极时，如图7(a)所示，其在运动过程中，多次与绝缘子表面发生碰撞并停留在平面区。仅当微粒与交界区发生过碰撞时，非平面区才会存在明显的正电荷斑，最大电荷密度为4.5 pC/mm2，如图7(b)所示，在微粒最终静止的位置则未观察到电荷斑的存在。

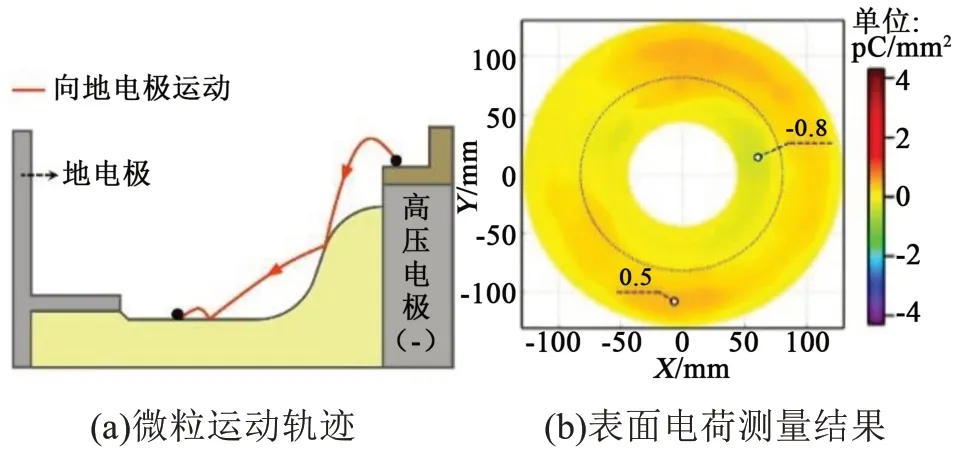
图6 金属微粒通过方式1运动最终静止在平面区Fig.6 Metal particles move through mode 1 and finally rest in the plane region

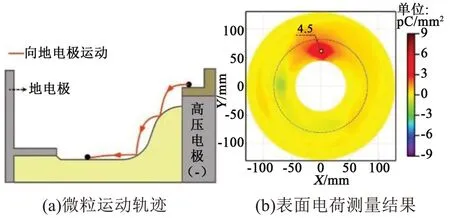
图7 金属微粒通过方式2运动最终静止在平面区Fig.7 Metal particles move through mode 2 and finally rest in the plane region

此外，还存在两种特殊的情况，即金属微粒最终停留在交界区处，如图8(a)和9(a)所示。此时，无论微粒以方式1 或2 离开高压电极，绝缘子表面都会出现明显的正电荷积聚。当微粒以方式1离开电极时，非平面区内出现了面积较大的正电荷斑，最大电荷密度为5.5 pC/mm2，如图8(b)所示。当微粒以方式2 离开电极时，非平面区形成了最大电荷密度为11.6 pC/mm2的正极性电荷斑，如图9(b)所示。与方式1相比，其电荷密度幅值更大，表明微粒以先滚动后启举的方式离开高压电极对表面电荷积聚特性的影响更明显。

图8 金属微粒通过方式1运动最终静止在交界区Fig.8 Metal particles move through mode 1 and finally rest in the junction area

图9 金属微粒通过方式2运动最终静止在交界区Fig.9 Metal particles move through mode 2 and finally rest in the junction area

综上所述，当初始位置在高压电极的金属微粒在振动作用下发生运动，且微粒最终静止在交界区或微粒以方式2 弹出且在碰撞到交界区时，均可能在绝缘子非平面区形成正极性的电荷斑。

当金属微粒的初始位置位于地电极时，同样观察到如前所述的两种离开电极的方式。微粒以方式1 和2 弹出，并最终静止在交界区时的运行轨迹如图10(a)和11(a)所示，可见两种情形下微粒的运行轨迹相似。此外，这两种情形下，均导致绝缘子非平面区形成了较大的正极性电荷斑，如图10(b)和11(b)所示，最大电荷密度分别为5.2 pC/mm2和12.1 pC/mm2。显然，以方式2 离开电极的微粒诱发了更为明显的电荷积聚现象。若微粒离开地电极后，最终静止在绝缘子的平面区，其能否引发明显的电荷积聚与微粒的运动方式有关。当微粒以方式1离开接地电极时，并不会引起表面电荷的明显积聚，电荷分布特征与图6(b)类似，最大电荷密度小于1 pC/mm2，故未示于文中。而当微粒以方式2 离开地电极时，如图12(a)所示，微粒与交界处碰撞，使非平面区形成了幅值为9.0 pC/mm2的正极性电荷斑。此外，也可能出现如图13 所示的特殊情况，即微粒从交界处反弹后最终静止在地电极附近，其端部与地电极的距离小于3 mm，最大电荷密度为4.4 pC/mm2。可见，当初始位置在地电极的金属微粒受振动作用向绝缘子运动时，在交界处静止或滚动-启举-碰撞交界处会导致非平面出现电荷积聚，若微粒静止位置与地电极的距离较小时，在微粒附近的平面区也会出现明显的电荷积聚现象。

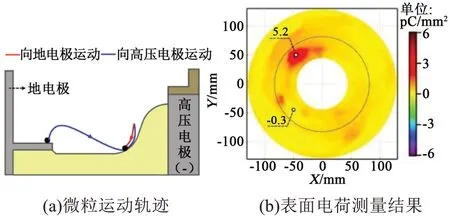
图10 金属微粒通过方式1运动最终静止在交界区Fig.10 Metal particles move through mode 1 and finally rest in the junction area

图11 金属微粒通过方式2运动最终静止在交界区Fig.11 Metal particles move through mode 2 and finally rest in the junction area

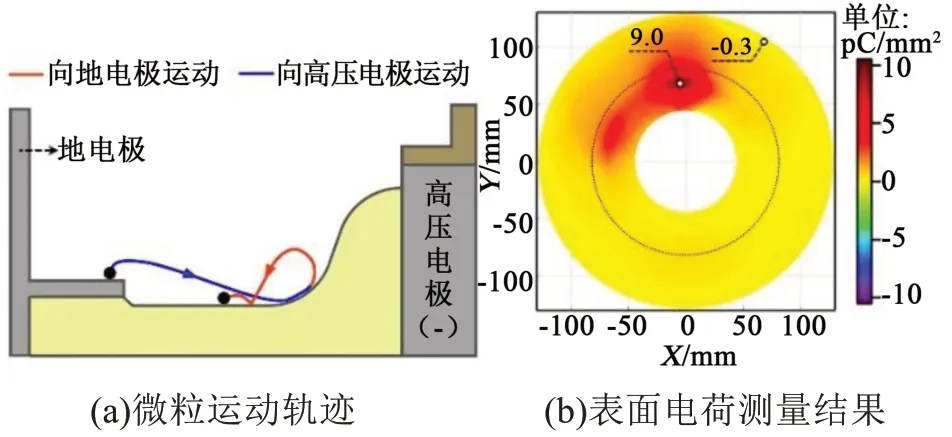
图12 金属微粒通过方式2运动最终静止在平面区Fig.12 Metal particles move through mode 2 and finally rest in the plane region

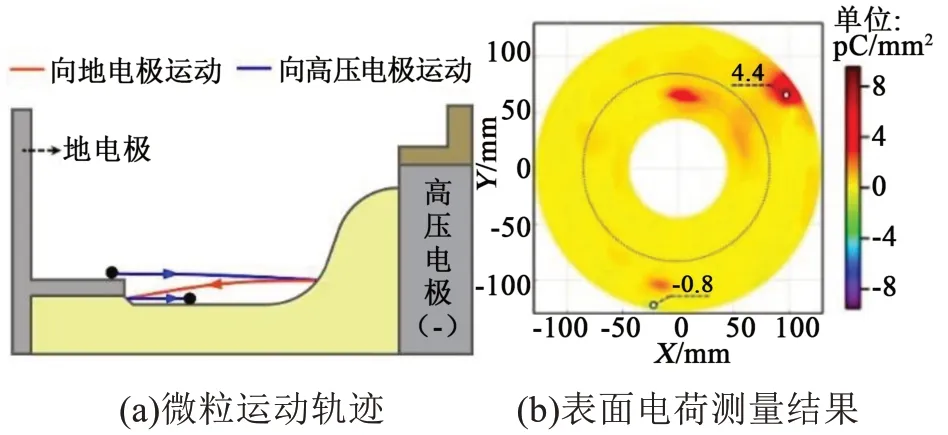
图13 以方式2运动的金属微粒最终静止在地电极附近Fig.13 Metal particles finally rest near the ground electrode by mode 2

3 振动诱发金属微粒弹跳对表面电荷积聚的影响机理分析

当GIS/GIL 中存在金属微粒时，振动可能导致原本静止的微粒产生运动，降低微粒的启举电压，同时也会改变微粒的启举方式[24]。故振动将通过改变金属微粒的带电荷量和运动轨迹来影响表面电荷的积聚特性。需要注意的是，金属微粒的启举、迁移等动态过程与其所处的气体氛围有关，空气介质和SF6中金属微粒的启举电压等参数存在差异。但本文研究的重点并非金属微粒的启举及运动的机理，而是微粒运动前后的位置变化导致的电场畸变、诱发气体电离和电荷积聚的过程。因此，采用更易电离的空气介质将有助于分析电荷积聚的机理。

3.1 启举方式对表面电荷的影响

金属微粒的带电荷量对表面电荷积聚的影响，在实验中体现在微粒启举方式的差异上。采用COMSOL 软件建立圆盘绝缘子三维模型，在-30 kV下开展有、无金属微粒时的电场仿真。振动前，线形微粒平置于电极表面并带有与电极极性相同的电荷，其带电量q为式（1）。

式（1）中：a和l分别为微粒的半径和长度；E为微粒所在位置的电场强度。以距电极边缘的距离为横坐标，无金属微粒时，高压和地电极表面电场强度的仿真结果如图14 所示。由图14 可见，电极边缘的电场强度最高，且场强随距电极边缘的距离增加而迅速降低，距离地电极x=5 mm 处的电场强度仅为边缘处的21.9%，距离高压电极x=5 mm 处的电场强度仅为边缘处的34.6%。因此，当微粒以直接在初始位置启举的方式（即方式1）离开电极时，其带电量低于方式2中微粒的带电量。故金属微粒以方式2 运动比以方式1 对绝缘子表面电荷积聚的影响更大。

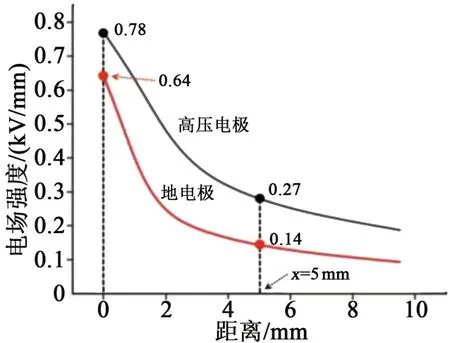
图14 高压电极与地电极表面电场分布曲线Fig.14 Surface electric field distribution curves of high voltage electrode and ground electrode

3.2 静止位置对表面电荷的影响

研究表明，当金属微粒处于绝缘子表面的不同位置时，其对电场畸变的影响存在差异。微粒距绝缘子表面越远，其对表面电荷积聚的影响越弱[25-26]。本文针对金属微粒位于绝缘子表面不同位置时的电场分布进行分析，共选取7个点，其中4个点位于非平面区，3个点位于平面区。依次将不带电微粒和金属微粒A～D 放置在所选取的碰撞点进行仿真，根据3.1 节的分析，以方式1 离开电极的微粒带电量要低于以方式2 离开电极的微粒，同时两电极的电位和结构的差异也会导致微粒带电量不同。令微粒A 初始位置在地电极，以方式1离开电极，其带电量为9.8×10-12C；微粒B 初始位置在地电极，以方式2 离开电极，其带电量为4.5×10-11C；微粒C 初始位置在高压电极，以方式1 离开电极，其带电量为-1.9×10-11C；微粒D初始位置在高压电极，以方式2 离开电极，其带电量为-5.5×10-11C。微粒中心的横坐标与所选取点的横坐标重合，提取仿真结果中的最大场强模值，可得如图15所示的电场分布。由图15 可见，当微粒从高压或地电极弹出时，电场畸变最严重的位置均在A1 区。未带电的金属微粒也可使其附近的电场发生不同程度的畸变，以从地电极弹出的微粒为例，当微粒在交界区A1 时畸变程度最高，最大场强为2.6 kV/mm，为无微粒存在时的5.9倍。

图15 微粒位置与带电量对绝缘子表面电场分布的影响Fig.15 Influence of metal particle position and charge on the surface electric field distribution of spacer

当金属微粒带电时，根据静电感应原理，靠近带负电的高压电极的微粒尖端积聚正电荷，其附近的电场方向为从空气指向绝缘子；微粒的另一端积聚负电荷，其附近的电场方向为从绝缘子指向空气。微粒所带净电荷极性为正，且同轴圆柱电极下的电场存在梯度，因此靠近高压电极的微粒端部对电场畸变更严重，易引发气体电离。如图15(a)中所示，带电微粒A 对交界区电场畸变的影响比不带电微粒更加严重，当其仅碰撞但未静止在交界区时，最大场强为3.3 kV/mm，达到了空气电离场强3 kV/mm[27]，但电场强度幅值不高，电离程度较弱，且电场被加强的时间较短，因此难以在绝缘子表面观察到明显电荷积聚。当微粒静止于交界区附近时，非平面区正电荷积聚机理示意图如图16所示，微粒周围的气体中会持续产生大量自由电荷，其中的正电荷会在法向电场的作用下向非平面区迁移，使气体侧传导在与体传导的竞争中占据优势，因此在非平面区积聚正极性电荷斑[26]。电离产生的负电荷在平面区较强的切向电场的作用下，向地电极迁移并泄入大地。当微粒经过或静止在绝缘子表面其他区域时，其引起的最大场强均未超过3 kV/mm，不会发生气体电离，故未静止在交界处的金属微粒不会导致明显的电荷积聚。带电金属微粒B在交界区附近的电场高达4.0 kV/mm，相比于微粒A，其畸变电场的程度以及带电量都较高。当微粒B仅碰撞但未静止到交界区时，虽然气体电离的时间短，但很剧烈，故在非平面区有电荷斑出现。当微粒B 最终静止在交界处时，微粒周围的气体电离剧烈且时间长，导致空气中正电荷密度较高，故图11(b)中非平面区的最大电荷密度高于图10(b)。