深入探讨化繁为简 一题多解浸润素养——以一道高考函数题的多解为例

重庆市第八中学校 (401120) 毛 闰 谢 强 胡 艺

一、引言

函数是高中数学的主要内容，也是一个教学难点，其内容广泛，考查形式丰富，具有较强的综合性.导数作为兼具代数运算和几何意义的一个重要概念，是研究函数性质和解决有关函数问题的有力工具，所以函数和导数的结合能够很好地考察学生思维的严谨性、综合性等特点，同时它也是逻辑推理、数学运算等数学核心素养的重要载体.运用导数解决不等式含参恒成立问题是高考的一个常考点，也是学生学习导数章节时必须掌握的题型之一.本文对2010年高考新课标数学理科21题第(2)问的多解进行探讨，践行此类题求解“有法可循、有法可依、有法可试”的理念，由此提升学生解决此类问题的信心和眼界，发展学生的数学核心素养.

二、问题求解研究

题目(2010年高考新课标数学理科21题)设函数f(x)=ex-1-x-ax2.

(1)若a=0，求f(x)的单调区间；

(2)当x≥0时，f(x)≥0，求a的取值范围.

解析：(1)当a=0时，f(x)=ex-1-x，f′(x)=ex-1.当x∈(-∞,0)时，f′(x)<0；当x∈(0,+∞)时，f′(x)>0.故f(x)的单调减区间为(-∞,0)，单调增区间为(0,+∞).现着重探讨与研究第二问的解法与思路，开拓学生思维，增强学生的数学能力.

(一)直接处理，分类讨论

第(2)问是一个不等式含参的恒成立问题，并且由于求导后导函数依然是超越函数，不容易判断零点，需考虑再对导数求导.因此，不确定性以及要想到求二阶导是本题的难点.所以需要对参数进行分类讨论，将不确定性问题转化为确定性问题来解决.

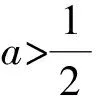
评注：本解法思路相对简单，主要是想求出f(x)的最小值，为此需要判断单调性，自然而然就想到了求导，但求导后依然判断不了导函数的正负性，由于二阶导是可以研究一阶导的性质，所以笔者尝试着求二阶导，然后通过分类讨论解决此问题.但解法一的不足之处在于通过多次求导才解决此问题，能否只求一阶导就可解决此问题？

评注：为了减少求导次数，解法中想到对函数y=φ(x)ex+n(其中n为常数)求导后正负性与ex无关，故对f(x)≥0进行变形.虽然本解法只求一阶导就可以把问题解决，但不足之处在于讨论的情况变得复杂了.

(二)紧扣“上文”，巧妙放缩

很多学生在处理问题时，不会“瞻前顾后”，联系上下文.实际上，本题的第一问有命题者的意图，这也间接考察到逻辑推理的数学核心素养.f′(x)=ex-1-2ax不好处理的原因在于ex-1-2ax=0是超越方程，不易求解，但通过第一问易知ex-1≥x，由此想借助这个不等式进行放缩处理.

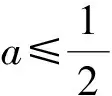
评注：放缩法是高中数学证明不等式的一种非常重要的方法，适当放缩可以简化问题.本解法通过借助第一问巧妙放缩后，明显比前两种解法简化了许多，不仅只需求一次导即可解决问题，而且减少了讨论情况.

(三)分参处理，避免讨论

处理含参恒成立问题一般两种办法，一是直接法，另一个就是分离参数.但是分参也需要注意，一是要证明的式子能否分参？二是分参处理真的会使问题简化吗？只有通过实践，大胆的尝试、小心的求证后才能下结论.

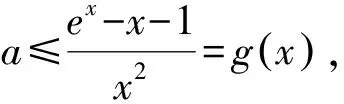
评注：虽然通过分参避免了讨论，但有几个难点，一是最后g(x)在x=0处无意义，需通过极限来求其下界，且用到了洛必达法则；二是求导后依然不好判断g′(x)的符号，以至于还需进一步处理，解法中想到g′(x)正负性只和g′(x)的分子有关，此时要么对g′(x)的分子求导，但求导之后的超越函数依然不好判断正负，还需再求导，这也是此法的一个难点.

(四)数形结合，妙用相切

数形结合可以让我们很直观的感知函数的变化趋势，直观的理解抽象的数学问题.因此，在解决不等式恒成立求参数范围问题时，可以将不等式拆成两个容易做出图像的函数，通过函数图象确定两式大小关系，或借助ex-1≥x，x-1≥lnx等常见不等式，通过函数图像的切线进行放缩，放缩时要关注函数图象在某处的切线，大胆猜想，小心求证.

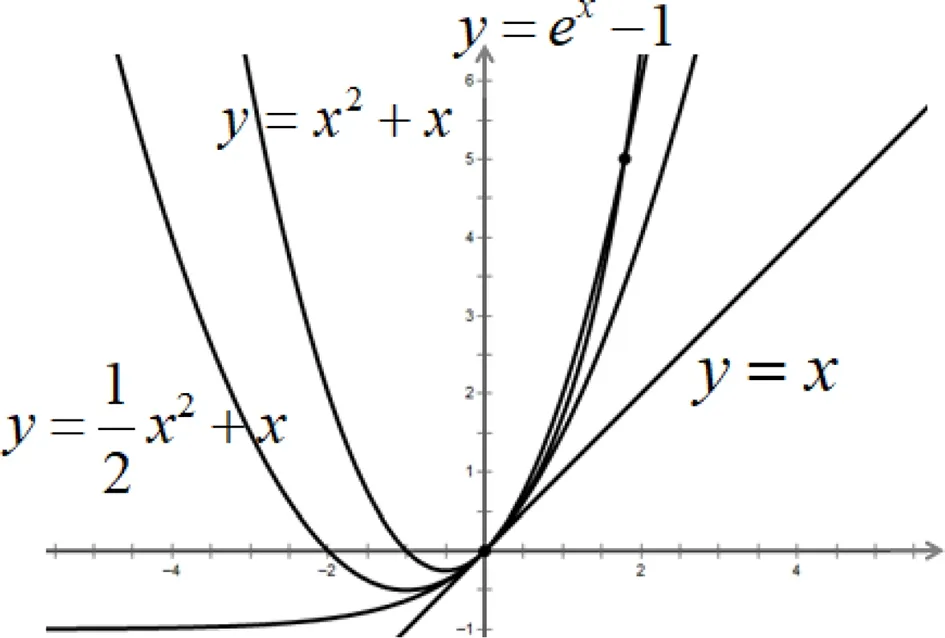
图1

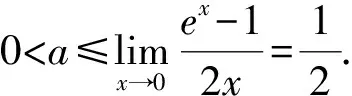
评注：本解法虽然能通过适当变形后，转化为熟悉的二次函数和指数型函数，同时关注切线位置，快速解决问题.但此法有几点不足之处：一是图形只能直观感知，但并不严谨，所以只适用于解决小题以及对大题起到辅助作用；二是虽然拆分的两个函数图象容易画，但是由于两个函数图象均为曲线，并不能很好的解释说明和直观感知.

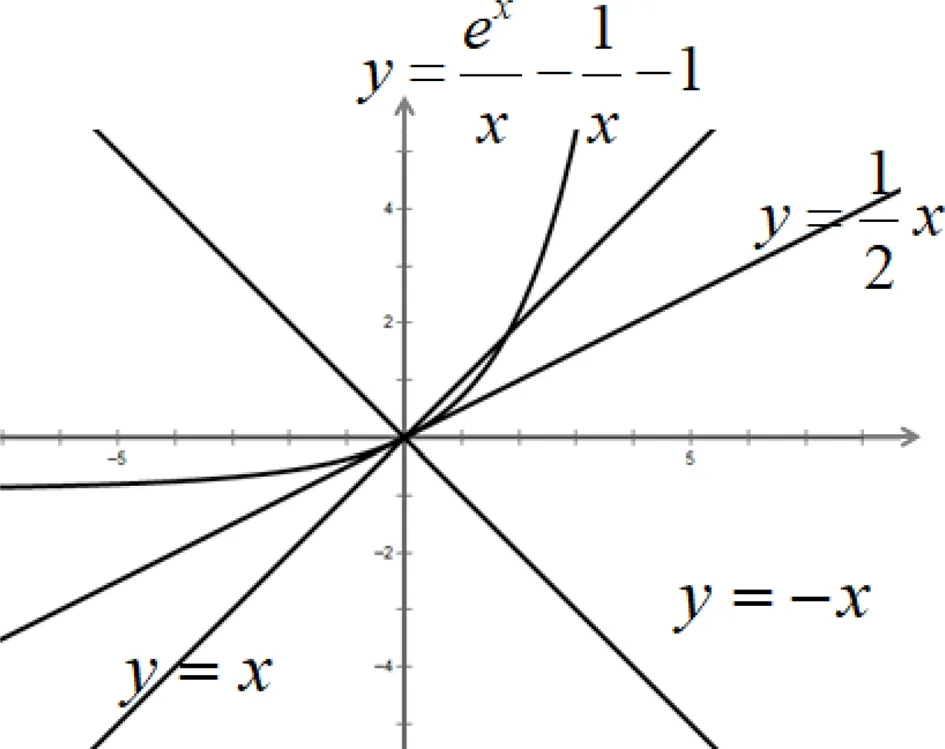
图2

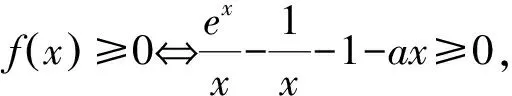
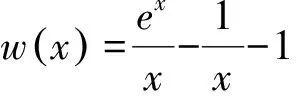
评注：此法与解法五对比，明显可以通过函数图象更加直观感受到a的取值范围变化时两函数之间的大小关系.

(五)大学视觉，拓展思路

对于此题，我们还可以从微元角度来探讨，给出以下解法.

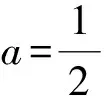
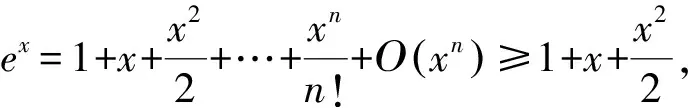
评注：“站得高，看得远”，我们应该站在一个更高的角度来看待问题，这样既可以拓展思路，发散思维，提升素养，同时又能看清事物的本质.数学知识不只局限于中学知识，也不只局限于大学知识，还有很多未知的数学知识和方法，都值得我们去探寻.

三、反思总结

在抽象的意义下，一切科学都会是数学的应用；数学这样美妙的学科，揭示无形的灵魂，赋予真理以生命，为思想增添光辉.数学的重要性不言而喻，解题又是学习数学环节的重要环节，罗增儒教授对数学解题水平做了划分，其中第4水平为：能自觉通过解题分析增强数学理解、提高数学素养.进行自觉的解题反思，通过分析“怎样解题”而领悟“怎样学会解题”.数学问题的迅速识别，解题思路的主动设计，知识资源的理性配置，解题方法的灵活运用，解题策略的适宜调控，解题过程的自觉反思，努力通过解题获得数学的理解，使认识进入深层结构.能从数学操作和正确答案中看到数学知识和数学方法的应用，能从数学思想和思维策略中提炼数学核心素养.对于一题多解的探寻与研究，正是朝着这“第4水平”的方向前行.