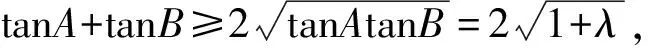对一道质检题错解的剖析及探究

福建师范大学附属福清德旺中学 (350319) 杨 吉 周 宁

2022月5月福州进行高三质检，其中第20题为解三角形问题.该题以三角形为载体考查正弦定理、余弦定理等知识，该题推陈出新，脱离常规的边角转换思路，需要学生结合图形进行条件转化，是很好的试题.遗憾的是，命题者对条件的理解不够，导致解答出错.本文展现其错解，并对该题进行一些延伸拓展.

一、试题呈现

记△ABC的内角A，B，C的对边分别为a，b，c，已知sinC=2sinAsinB，点D在边AB上，且CD⊥AB.

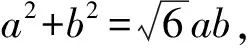
二、解法赏析

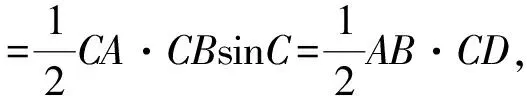
厦门叶超杰老师在上述解法的基础上对角C的两解进一步判断：

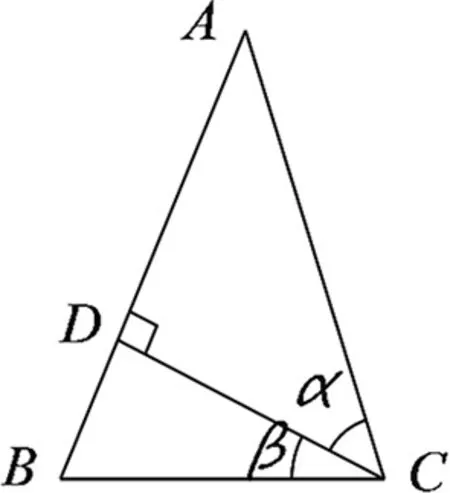
图1

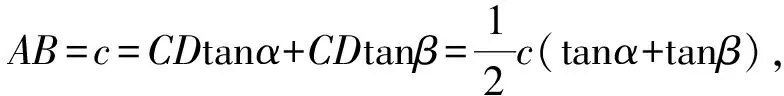
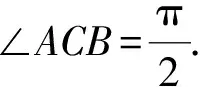
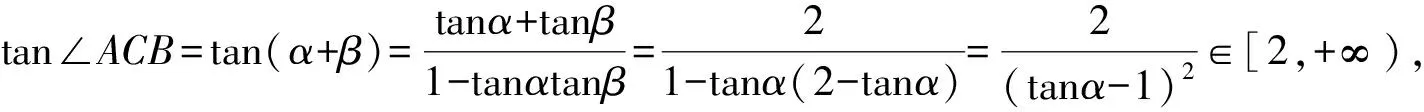
三、问题剖析

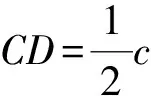
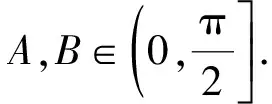
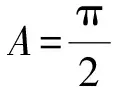
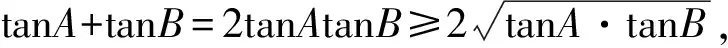
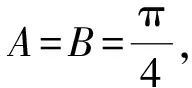
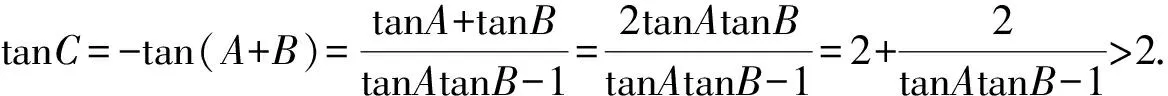
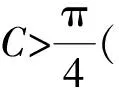
四、拓展延伸

从上述问题的辨析我们看出，命题者的解答出错的原因在于对sinC=2sinAsinB条件认识不够充分导致未对多解进行检验排除.也就是说，在锐角△ABC中，形如sinC=2sinAsinB结构就蕴含角C的范围限制.因此笔者对该条件作一些改变，进行拓展探究.

探究一在锐角△ABC中，sinC=λsinAsinB，求tanC的取值范围.

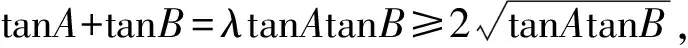
探究二在锐角△ABC中，sinC=λcosAcosB，求tanC的取值范围.

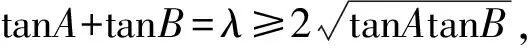
探究三在锐角△ABC中，cosC=λsinAsinB，求tanC的取值范围.

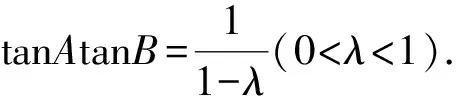
探究四在锐角△ABC中，cosC=λcosAcosB，求tanC的取值范围.