约束阻尼板双线性材料插值法拓扑动力学优化

2022-12-25贺红林赵伟鹏余志豪龙玉繁鄢殷期

中国机械工程 2022年23期

贺红林赵伟鹏余志豪龙玉繁鄢殷期李冀

南昌航空大学航空制造工程学院，南昌，330063

0 引言

板壳结构在航空航天、船舶工程、车辆运载等众多领域中应用非常广泛，如何抑制其有害振动一直是板壳设计非常关注的问题[1]。现有的各种板壳结构控振方法中，基于黏弹材料的表面处理方法因具高阻尼性，既能有效控制结构的宽频振动，又能最大限度地减少对结构动力学特性的影响，而成为普适性的板壳抗振方法[1]。在板壳表面的全域敷设阻尼材料必使质量大增，有悖于轻量化设计原则，故如何有效发挥阻尼材料的效能，一直为该领域的热点问题。文献[2]将微结构引入阻尼板并采用均匀化法进行优化，但该方法涉及的优化变量过多、计算量巨大，故不实用；文献[3]研究了移动渐近法阻尼板优化；文献[4]探讨了飞机进气道壁板变密度法黏弹减振优化；文献[5]引入指数函数材料插值模型并利用变密度法解算阻尼板优化构形；文献[6]采用水平集法优化阻尼板并探讨了阻尼层厚度对模态损耗因子和最优构形的影响；文献[7]以声压为目标实现阻尼板优化；文献[8]基于结构能耗目标求得压电振动板的最优压电布局；文献[9]引入LOG插值模型求解阻尼板构形；文献[10]研究了合理近似插值(RAMP)意义下的圆柱壳振动优化；文献[11]利用伴随变量瞬态响应灵敏度分析法实现阻尼板优化。

上述文献除[2]、[3]、[6]外，其他以变密度为优化思路且优化目标函数取定优化目标之倒数，从而使迭代计算量大，且采用的材料插值模型不仅无法抑制灰度单元出现而且征罚单元时带有明显偏惠性。为此，本文构建差值型目标函数，并引入双线性材料插值模型，有效实现无偏性惩罚，较好地解决灰度单元问题。

1 拓扑动力学优化模型

为获取理想阻尼材料布局，须先建立便于有限元法解算的阻尼板优化模型。为此，构建以移动常数与模态损耗因子之差值为目标函数、阻尼材料用量以及模态频率变化量为约束的阻尼板差值型优化数学模型，表达为

(1)

考虑到板振动时，各模态的振动贡献度不同，故在优化目标函数中引入权值以便突出对主要模态的振动抑制。可根据模态参与度确定各权值的大小。

2 单元灵敏度分析

有限元法适于阻尼板拓扑动力学优化中的力学参数求解，用它解算结构模态应变能时，不仅可避免复特征值及其特征向量的推导，且具较高计算精度，而模态损耗因子与模态应变能间的关系为

(2)

为推进阻尼板优化迭代，须确定优化目标函数对拓扑变量的灵敏度。拓扑迭代中，基于该灵敏度构成的方向矢量可为拓扑构形演进指明方向，而目标函数对拓扑变量的灵敏度为

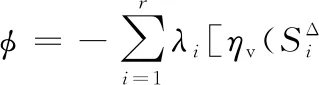
(3)

为便于书写，这里引入微分算子∇=∂(·)/∂xl。根据振动理论，对于线弹性力学行为主导的阻尼板，其振动参数满足以下关系及振型正交条件：

(4)

对式(4)进行求导、变换及整理后，可得

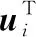
(5)

进而可推演出阻尼层、约束层模态应变能灵敏度：

(6)

式中，下标v、c分别对应阻尼层和约束层；Mv、Mc为阻尼、约束层质量矩阵；Kv、Kc为相应的刚度矩阵。

将式(3)、式(5)、式(6)联立求解，可得

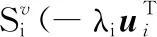
(7)

3 双线性材料插值模型

拓扑动力学优化的一个突出问题是灰度单元问题。若迭代中不能避免大量灰度单元出现，则优化结果难以实施。为解决该问题并避免拓扑迭代中的偏惠性单元惩罚，本文从数学意义出发，构造具对称极化特征的双线性材料插值模型：

En(xi)={ep(xi-t)/[1+ep(xi-t)]}E00≤t≤1

(8)

式中，E0、En分别为插值前后的弹性模量；t、p分别为分界因子和惩罚因子。

图1展示了t、p对惩罚函数的影响，p值越大则曲线斜率越大，惩罚效果越强；若固定p值，则不同t值对应的曲线存在不同的中间密度分界点。这表明，可视情形取定t值，以微调密度分界点而使密度向0、1等概率极化。尽管迭代时惩罚施加于弹性模量，但其效果却在单元刚度矩阵和质量矩阵上得到反映，如下：

(a)惩罚因子的影响(t=0.5)

(9)

式中，k0，i、ki分别为迭代前后的单元的刚度矩阵；m0，i、mi为相应的单元质量矩阵；q为适当取定大于1的系数。

根据结构总刚度矩阵构筑理论并考虑基层的拓扑不必迭代，可得双线性插值时的刚度矩阵与质量矩阵：

(10)

式中，Kb、Kv0、Kc0分别为基层刚度矩阵、阻尼层初始刚度矩阵、约束层初始刚度矩阵；Mb、Mv0、Mc0为对应的质量矩阵。

式(10)对设计变量求导可得

(11)

将式(7)、式(11)联立求解，可得双线性插值模型时的阻尼板目标函数灵敏度：

(12)

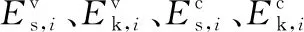
4 优化模型的求解

4.1 拉格朗日乘子法迭代

变密度拓扑优化的基本前提是目标函数的凸性，模态损耗因子型函数不满足该条件，若用常规优化准则法寻优会陷入局部优化，故根据序列凸规划理论，引入移动参数构造目标函数的凸性逼近函数，对逼近函数寻优可求取全域优化构形。为此，基于式(1)构造拉格朗日函数：

(13)

式中，Λ、βi、γi为拉格朗日乘子。

引入移动参变量c并构造φ=φ*+cV、Λ=Λ*-c，且将这两个式子代入式(13)，再利用K-T条件，可得

∇φ*+Λ*∇V-βi+γi=0i=1，2，…，ne

(14)

(15)

式中，ξ>0；φ0为常数。

式(15)对yi求导，有

(16)

将式(16)的两边对xi求偏导并进行整理，可得

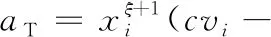
(17)

式(16)表明，只要aT>0，则φ*具凸性。明确了此凸性条件后，便可对式(13)中的拓扑变量迭代域进行细分，并设定自变量极小值集Ωmin、中间值集Ωmid、极大值集Ωmax，则式(13)变为

(18)

对式(18)运用K-T条件进行计算，得到动态逼近凸性函数的拉格朗日乘子法的迭代格式：

(19)

式中，ϑ为移动更新极限值；k为迭代步数。

4.2 数值不稳定问题的处理

阻尼板拓扑优化可能存在棋盘格、振型紊乱及网格依赖等问题，在此引入绕单元均值法解决这些问题，即针对当前处理单元求取围绕它的各单元灵敏度的加权均值，并以该值作为当前单元的灵敏度。当前单元的灵敏度为

(20)

Hi=rmin-dist(i，j)

式中，Hi为权值；rmin为单元围绕半径；dist(i，j)为单元i、j间距离；nT为处于围绕半径内的围绕单元i的单元总数。

通过振型跟踪，可以防止优化模态的振型异形化，避免因模态阶次跃迁而造成优化目标模态混乱。为此，针对每次迭代后的阻尼板优化模态与迭代前的初始目标模态做模态置信度(MAC)计算，相应的计算式为

(21)

其中，φi，0、φi，k分别为阻尼板在优化前及在当前迭代步之内的归一化模态振型，并且当A=1时，φi，k与φi，0振型形态完全相同；当0.9≤A<1时，φi，k与φi，0存在较小差别；当A<0.9时，φi，k与φi，0存在明显差别。模态置信度A值越小则φi，k、φi，0振型相差越大。另外，考虑在阻尼板优化过程中，一旦拓扑变量在相邻两迭代步内的取值相差非常大，则会造成不合理单元刚度，引起模态振型畸变。为此，还需对接续两个迭代步内优化出的模态振型计算置信度Ak，并在迭代中通过微调移动更新值以保证Ak≥0.95。Ak计算式为

(22)

5 算例分析与验证

5.1 算例分析

为了明确差值型优化数学模型及双线性材料插值优化法的效能，利用ANSYS APDL分别编写了基于双线性、各向同性惩罚微结构法(SIMP)及RAMP材料插值模型的悬臂式阻尼板的拓扑动力学优化程序。该板的位移边界条件是左端固支、右端自由，如图2所示，相关的几何和物理特性参数如表1所示。

图2 阻尼板的位移约束模式

表1 约束阻尼板的基本参数

为求解阻尼板的结构动力学特性参数，利用八节点六面体单元Solid185对该板进行网格划分，基层、阻尼层、约束层采用同相的网格划分，且各层均划分出30×15个单元。

图3所示为基于不同材料插值模型求得的阻尼板优化布局，深红色区域为阻尼材料贴附区，深蓝色表示挖空区，其他区域为灰度单元区。可以看出，3种插值模型得到的密度云图大体一致，但是相较而言，双线性插值所得的密度云图颜色更分明、灰度单元极少，密度不稳定问题基本得以解决，更有利于优化构形重构及工程实施。这也表明，双线性材料插值不仅是可行的，而且具有更佳的密度极化效果。

(a)SIMP法1阶 (b)RAMP法1阶 (c)双线性法1阶

为进一步验证本文算法的性能，对模态损耗因子、模态频率的迭代情况进行了动态观测。图4所示为双线性插值时模态损耗因子的演进情况。可见，在迭代初期不管是针对单阶还是多阶模态优化，双线性插值均使模态损耗因子快速增大，当迭代至第6步时优化进程趋于平缓且模态损耗因子的变化趋稳；从密度云更迭来看，迭代中的灰度单元不断减小并在迭代末期消失殆尽，验证了本文优化模型及其解法的正确性；迭代前阻尼板的一阶损耗因子为0.158，经单模态与多模态优化后分别提高44.30%和52.59%。

图4 1阶模态损耗因子迭代历程

图5所示为双线性插值时的频率迭代情况。可见，在迭代的初期，各阶次频率均呈大幅度下降，在第5步时频率变化趋缓。就频变量大小来看，1阶频率降幅最大、3阶频率降幅最小，且单一模态的优化比多阶模态优化时降幅稍大。但总体上，频变量未超过10 Hz，这说明优化构形的频率处于允许范围内。图6所示为MAC值的更迭情况，可见，针对前3阶模态优化时，MAC值均在0.99～1间变化，未出现模态阶次逆转。

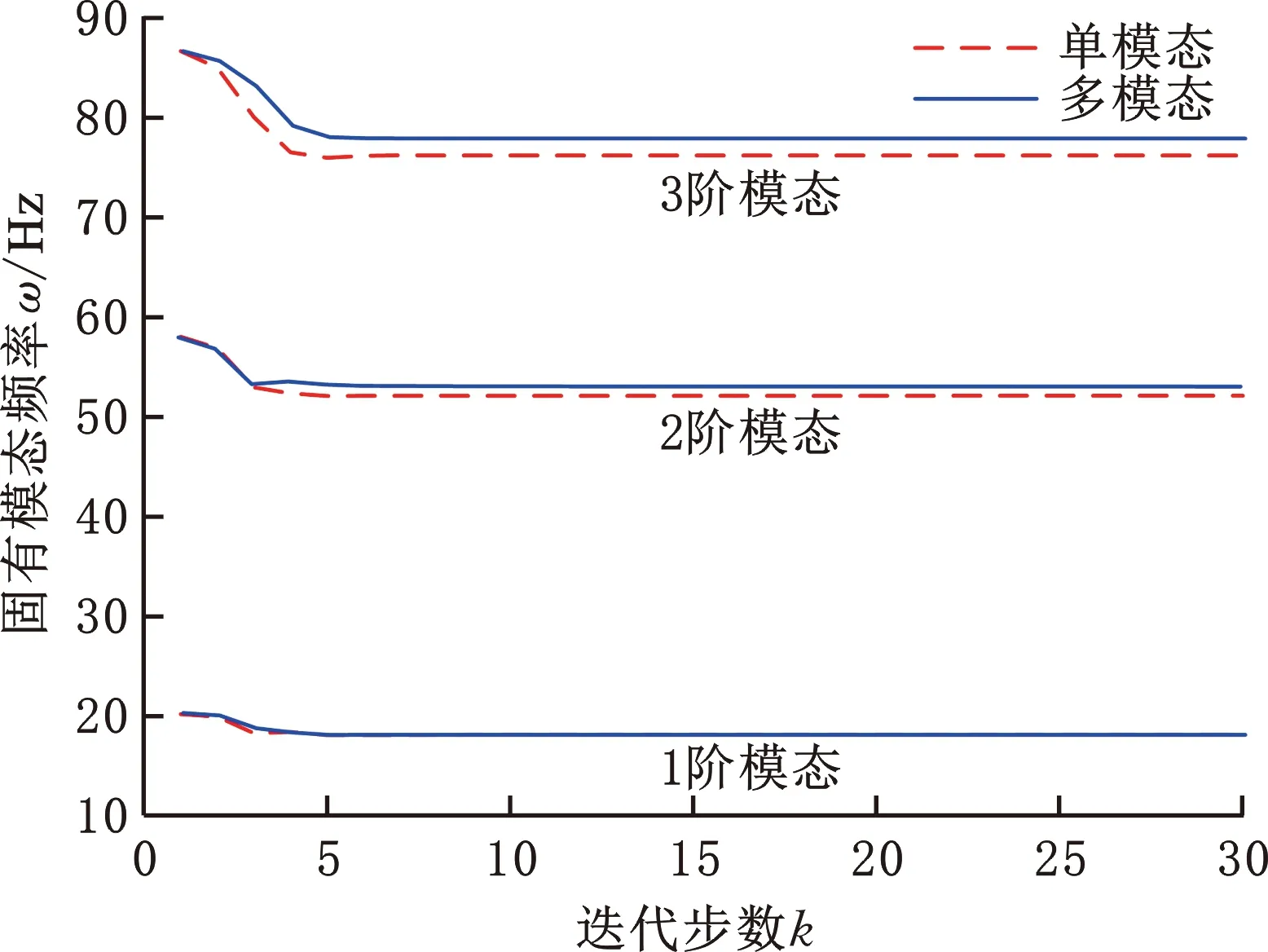
图5 模态频率的迭代进程

图6 优化迭代中的模态置信度变化

图7所示为不同体积约束比(材料删除率)条件下的模态损耗因子变化情况，当阻尼层从全覆盖到删除率达50%时，随着阻尼材料删除率的增大，模态损耗因子增大且多模态优化比单模态优化时模态损耗因子略大。图8所示为不同体积约束比下的优化构形中灰度单元占比，可见多模态优化时的灰度单元较单模态优化时的少，这表明，双线性插值的多模态优化能得到更清晰的优化构形。还可看到，双线性插值对灰度单元的确产生了明显极化效应，优化构形灰度单元占比很小，且该占比随删除率增大呈先降后增之势；模态损耗因子则随体积约束比减小而增大，当体积约束比为50%时达0.2284；体积约束比为70%时，则1阶优化密度云图中灰度单元几乎消失。不同体积约束比条件下的双线性插值模型优化结果如表2所示。

图7 不同体积约束比下的优化模态损耗因子值

图8 不同体积约束比下优化构形的灰度单元占比

表2 不同体积约束比下的双线性插值模型优化结果

为更充分地说明双线性插值对中间密度单元的极化效应，将双线性插值的灰度单元占比与SIMP、RAMP的灰度单元占比进行对比，结果如表3所示。可见，当采用双线性插值时，虽然1阶模态优化构形的灰度单元较2阶、3阶模态稍多，但也未超过1.78%。相反，SIMP、RAMP法的优化构形灰度单元占比高达12.44%，比双线性法大得多。可见，双线性插值优化构形的减振效果总体上优于SIMP和RAMP，这也说明双线性插值能较大程度实现中间密度值两向均匀极化。

表3 3种材料插值优化法的中间密度单元占比

时间复杂度是衡量算法性能的重要指标，为了体现本文优化算法的计算效率，对双线性法、SIMP、RAMP插值优化过程的计算耗时进行跟踪，结果如表4所示。由表4可看出，虽然这3种算法的计算耗时总体上比较接近，但是相对而言双线性法的耗时却更短一些，这充分说明双线性法在实现及执行效率上不存在问题。

表4 3种材料插值优化法的计算耗时

为了评判本文算法对阻尼板轻量化方面的贡献度，对于优化目标模态特定的模态损耗因子优化值，采用不同优化方法求取阻尼板迭代至该值时的优化构形，进而计算各种各构形的阻尼层材料体积删除率，结果如表5所示。本文在此对前3阶模态进行优化，3阶模态的损耗因子值依序设定为0.224、0.188、0.225。由表5可看出，不管针对哪个阶次模态的优化，双线性法的体积删除率均是最大的，这说明双线性法轻量化效果是比较理想的。需说明的是，考虑到优化构形实施时常将灰度单元做留存处理，故在计算删除率时将灰度单元排除在删除体积之外，这也是导致不同算法的删除率相差较大的又一原因。

表5 3种材料插值优化法的阻尼材料体积删除率

5.2 仿真结果验证

为了更好地印证本文方法的有效性，采用本文优化方法解算文献[5]中的阻尼板样例，该文献是以模态损耗因子倒数为优化目标并用SIMP求解。图9所示为本文方法得到的结果，将该结果与文献[5]进行对比可发现：本文的阻尼层构形与文献[5]中的密度云图大致相同，这意味着二者的黏弹阻尼材料敷设方式及敷设位置是吻合的，也就从另一个层面说明了本文方法的有效性。特别是，本文的密度云图中灰度单元较文献中少得多，这也说明双线性插值极化法是比较理想的。

(a)1阶 (b)2阶

从振动幅值随激励频率变化的关系中可以更直观地发现结构的减振效果，因此本文分别对优化前后的阻尼板进行有限元动力学建模和频率响应计算，幅频特性曲线如图10所示。由图10可见，优化后的阻尼板在各阶优化目标模态上的振幅较未优化时小得多，且1阶模态振幅下降幅度为13.1%，多阶复合模态振幅下降幅度为43.3%，表明了本文方法的有效性。