含自重载荷的功能梯度材料结构时域动力学拓扑优化设计

文桂林 陈高锡 王洪鑫 薛 亮 魏 鹏 刘 杰，

1.燕山大学机械工程学院，秦皇岛，066004

2.广州大学机械与电气工程学院，广州，510006

3.湖南大学机械与运载工程学院，长沙，410082

4.华南理工大学土木与交通学院，广州，510641

0 引言

具有良好力学性能的轻质结构设计近年来得到学术界和工程界越来越多的关注[1-3]，其中，功能梯度材料(functionally gradient materials，FGM)的力学性能可沿着一个或多个方向逐渐变化，具有相对于传统均一材料更多的设计自由度和更优异的力学性能，近年来被广泛应用于机械工程和航空航天等领域[1]。然而，传统经验设计方法很难最大程度地发挥FGM结构的最优机械性能。

结构拓扑优化方法通过寻求材料的最优分布可以设计出具有优良机械性能的FGM结构。NELLI等[4]首次提出了利用连续体结构拓扑优化来设计FGM结构，根据固体各向同性材料惩罚插值(solid isotropic material with penalization，SIMP)材料模型，提出一种新的材料模型FGM-SIMP来表示一个完全连续的FGM材料。在水平集方法框架下，XIA等[5]提出一种功能梯度结构拓扑优化设计新方法，实现了材料属性和机械性能的同时优化。采用凸规划求解策略以及周长控制方法，LI等[6]对具有拉胀特性的新型功能梯度蜂窝复合材料进行了拓扑优化设计。邱克鹏等[7]利用SIMP法实现了功能梯度MBB梁和功能梯度夹层结构夹芯的拓扑构型设计，并揭示了材料性能和材料插值模型对结构优化中材料分布的影响规律。李信卿等[8]对周期性功能梯度结构进行拓扑优化设计，获得了具有较好散热性能的FGM结构。虽然上述方法可以很好地提高FGM结构的机械性能，但都忽略了自重载荷和动力学特性，而面向重型机械装置、船舶和航空航天装备领域中FGM结构的设计时，自重载荷和动力学特性往往无法忽视。

已有研究对均一化材料组成的机械结构进行了考虑自重载荷的拓扑优化设计。CHEN等[9]提出了一种基于设计相关载荷的线弹性结构拓扑优化方法。BRUYNEEL等[10]研究了体积约束下柔顺度最小化结构拓扑优化问题，发现当结构自重占主导地位时，会出现柔顺度非单调性行为、最优结果无约束行为等，针对这些缺陷，张晖等[11]利用材料属性的有理近似(rational approximation of material properties，RAMP)材料插值模型和平均敏度过滤技术很好地解决了该问题。还有学者利用双线渐进结构优化方法和基于非均匀有理B样条基函数插值的拓扑描述函数方法，成功解决了考虑自重载荷的拓扑优化设计问题[12-13]。然而，上述研究大多针对均一材料的结构拓扑优化设计，而FGM的材料密度不均匀分布时，自重载荷对拓扑优化设计结果影响更大。

此外，考虑动力学特性的拓扑优化设计方法在机械工程领域得到了广泛的关注。OLIVER等[14]提出了一种增广拉格朗日法，以解决一般动态载荷作用下具有应力约束的结构拓扑优化设计问题。基于一种新的凝聚函数策略和时域求解结构动态响应的思路，ZHAO等[15]提出了一种新的拓扑优化方法，可以有效降低结构整个振动阶段最大动态响应。基于一种逐次迭代分析策略，KANG等[16]研究了考虑自然频率的动态大规模拓扑优化问题。综上研究发现，关于FGM结构的动力学拓扑优化设计研究较少。

基于此，本文提出了一种含自重载荷的功能梯度材料结构时域动力学拓扑优化方法。给出了针对FGM结构的自重载荷分配策略，研究了有/无自重载荷作用下，均一材料和功能梯度材料结构的优化构型差异性，并利用数值仿真和实验方法研究了均一材料组成结构在考虑自重载荷和无自重载荷作用下优化结构的动力学性能。

1 功能梯度材料结构的材料模型

在SIMP材料插值模型框架下，建立相对单元密度和功能梯度材料弹性模量、功能梯度材料密度之间的关系[4，7]：

(1)

式中，EH、ρH分别为FGM的弹性模量和密度；E0、ρ0分别为初始设定的弹性模量和密度；a、b为FGM材料梯度变化的相关设计参数；x、y为设定在FGM区域的坐标方向值；α为小于1的正实数，通常令α=15/16[15]；η为单元密度即设计变量；p为惩罚系数，通常令p=3，该惩罚系数可以有效地消除中间密度单元并推动拓扑优化趋向离散0-1解。

当a和b等于0时，FGM没有发生梯度变化，即相当于传统的均一材料，为功能梯度材料的特例。

如图1所示，FGM结构设计域离散后，单元弹性模量和单元密度分别为该单元中每个节点处弹性模量和密度值的平均值，即

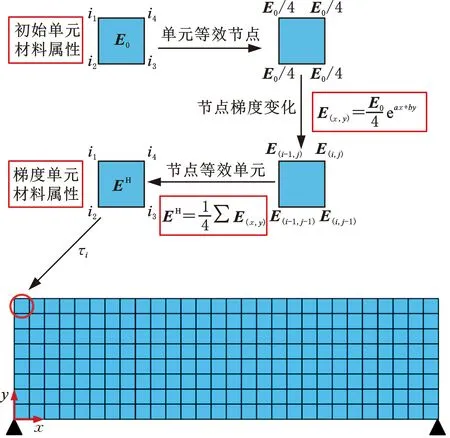
图1 二维功能梯度材料结构的材料分配策略

(2)

2 功能梯度材料结构自重载荷的分配策略

如图2所示，考虑4节点的四边形有限元网格和沿垂直y方向施加重力载荷，每个单元质量的四分之一分布在4个节点上，相邻单元质量在共同节点上叠加。由于功能梯度材料结构的材料属性呈梯度变化，所以功能梯度材料结构单元的自重载荷也呈梯度变化。因此，功能梯度材料结构受自重作用的单元载荷矢量为

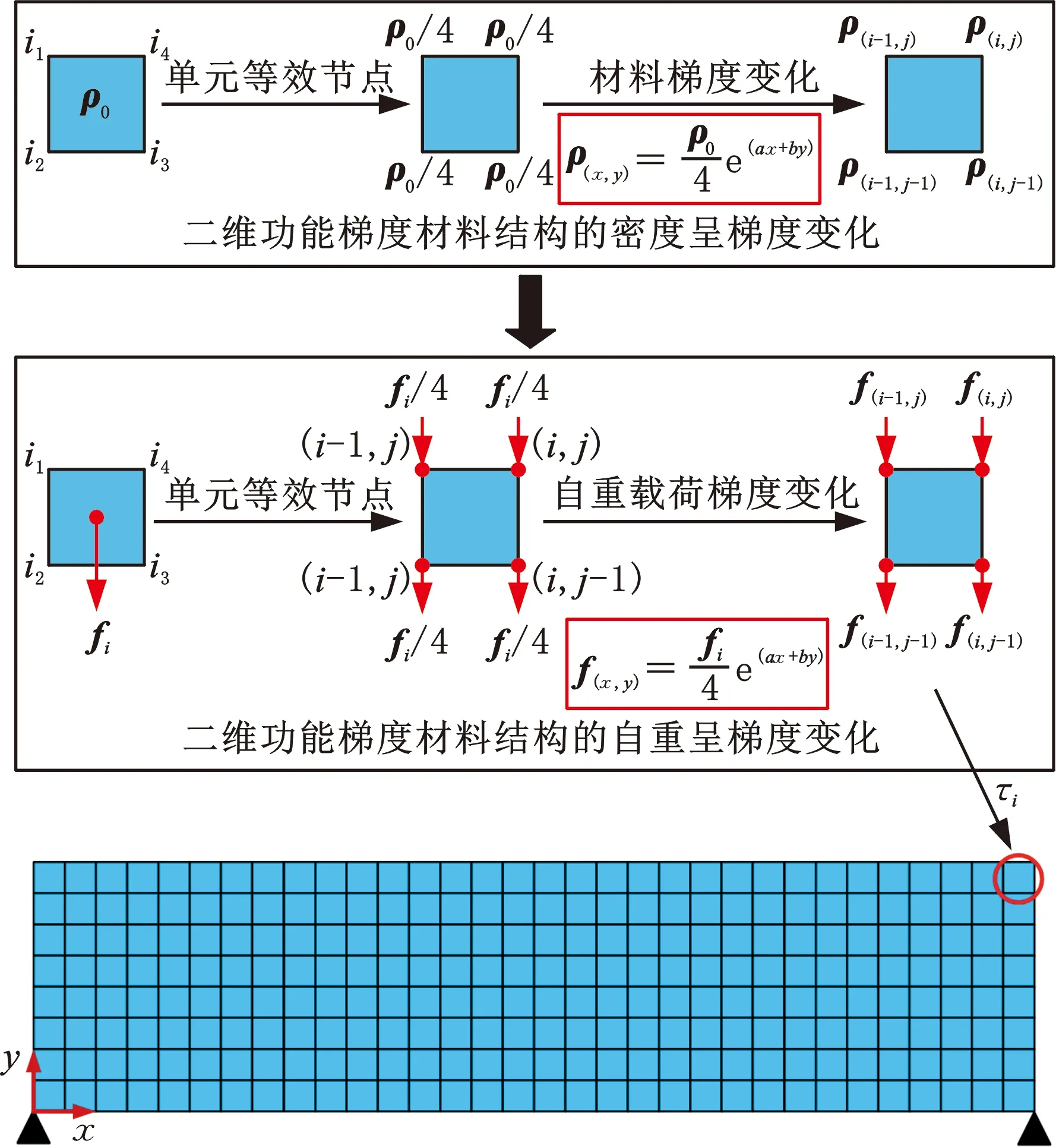
图2 二维功能梯度材料结构的自重载荷分配策略

(3)

式中，g为重力加速度；Vi为单元体积。

自重载荷相对于一个单元的变化可表示为

(4)

3 功能梯度材料结构动力学拓扑优化

3.1 拓扑优化模型

在上述材料插值模型和自重载荷分配策略的基础上，以动柔度最小为优化目标，以结构整体的体积为约束，建立FGM结构拓扑优化列式：

(5)

式中，MH、ZH、KH分别为全局质量、阻尼和刚度矩阵；N为单元数量；Ve为单元e的体积；Vmax为期望的总材料体积；为了避免有限元方程在求解过程刚度矩阵的奇异性，单元最小密度不取零，而是小的正数，ηmin=0.001；F(t)包括了自重载荷和外载荷；u(t)为在t时刻的结构位移响应；tf为外载荷加载时长；η为设计变量向量。

目标函数表达为

(6)

式中，C为结构柔度。

3.2 灵敏度分析

(7)

外载荷与设计变量无关，将∂f/∂ηe表示为自重载荷对设计变量求导，进一步可得

(8)

式(7)中引入伴随变量λ的微分方程为

(9)

(10)

s∈[0，tf]

Λ(s)=λ(tf-t)

求解出伴随变量，式(8)可进一步写为

(11)

设瑞利阻尼Z=αrM+βrK，且系数αr和βr相互独立，则

(12)

(13)

(14)

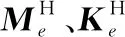
体积约束对设计变量的导数为

(15)

求得目标函数和体积约束对设计变量的灵敏度信息后，利用移动渐近线方法(the method of moving asymptotes，MMA)[17]可以对式(5)中的优化问题进行求解。

4 算例

算例中使用的参数如下：弹性模量E0=200 GPa，泊松比υ=0.3，密度ρ=7800 kg/m3，重力加速度g=9.81 m/s2，结构自重G=体积×密度×重力加速度×体积分数。多项插值模型中的惩罚系数p=3，α=15/16。动态载荷的单元时间步长Δt=0.005 s。瑞利阻尼系数αr=10、βr=10-5，动柔度单位为N·m。为了便于描述，将无自重载荷和考虑自重载荷的动力学拓扑优化设计分别简写为W/oSL(without self-weight load)和WSL(with self-weight load)。

4.1 均一材料二维结构算例

图3 二维两端固定梁结构和外载荷

图4所示为二维两端固定梁结构施加静态和动态载荷对优化结果的影响。其中，图4a所示是考虑自重的静力学拓扑优化结果；图4b～图4d所示分别为使外载荷激励时间tf为0.1 s、0.03 s和0.01 s时的WSL结果。表1所示为二维两端固定梁结构在加载时长tf=0.01 s时，不同外载荷(以与自重的比值量化)的优化结果，以及WSL和W/oSL的目标函数比值γ(γ=JWSL/JW/oSL)。

(a)静力学，J=7.602 N·m (b)tf=0.1 s，J=2.879 N·m

表1 加载时长tf=0.01 s，不同外载荷对优化结果的影响

由图4可知，动力学优化结果的目标函数值均小于静力学优化结果，且当加载时长较大时(如tf=0.1 s)，动力学优化构型与静力学优化构型近似，这与预期的一致；当加载时长较小时(如tf=0.03 s)，动力学优化构型明显异于静力学优化构型，加载时间越短(角频率越大)，构型差异越明显。由表1可知，受自重载荷的影响，优化结构的材料从固定端到外载荷施加点呈递减分布，这是由于重力使简支梁中间位置动态挠度变大，需要更多的材料分布到固定端以增加整体结构的动刚度。此外，当外载荷占自重比值逐渐变小时，动力学拓扑优化问题由自重载荷和外载荷共同作用变为自重载荷占主导，此时会有更多的材料向两侧固定端分布，且目标函数由2.291 N·m逐渐减小为0.339 N·m。此外，相同外载荷作用下，以WSL和W/oSL目标函数比值γ作为自重载荷对优化结构的影响程度指标，当外载荷占自重比值逐渐变小时，目标函数比值逐渐增大，与预期的结果一致。图5是在加载时长tf=0.01 s、外载荷F0=100%G时WSL和W/oSL的目标函数和体积约束的迭代过程图，可以发现，这两种情况目标函数均收敛良好，体积分数均收敛至50%。

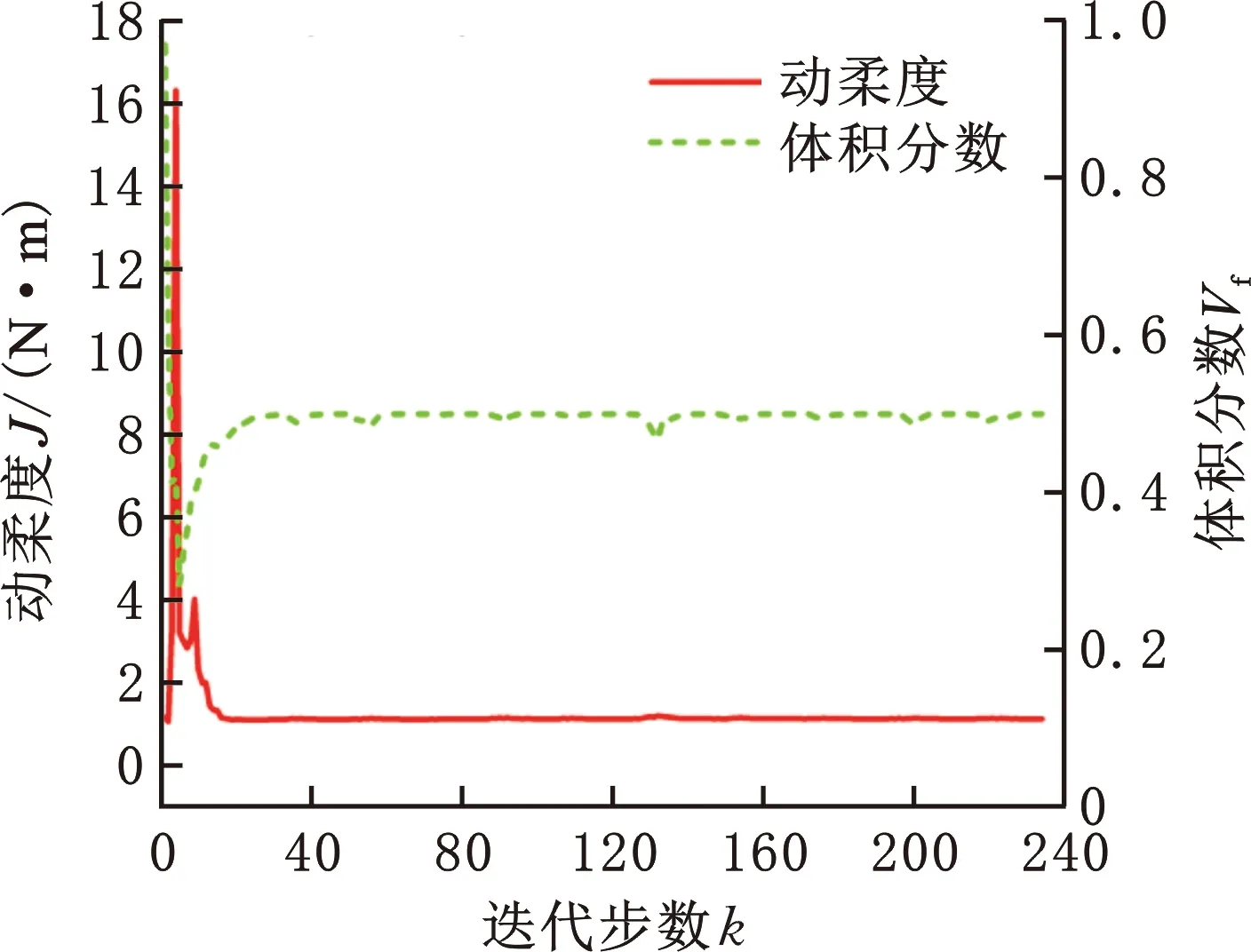
(a)WSL

4.2 功能梯度材料二维结构算例

初始设计域和边界条件均与4.1节一致，进行功能梯度材料算例分析。表2所示为两端固定二维梁结构在加载时间tf=0.01 s和外载荷F0=100%G时，不同类型功能梯度材料的WSL和W/oSL结果。

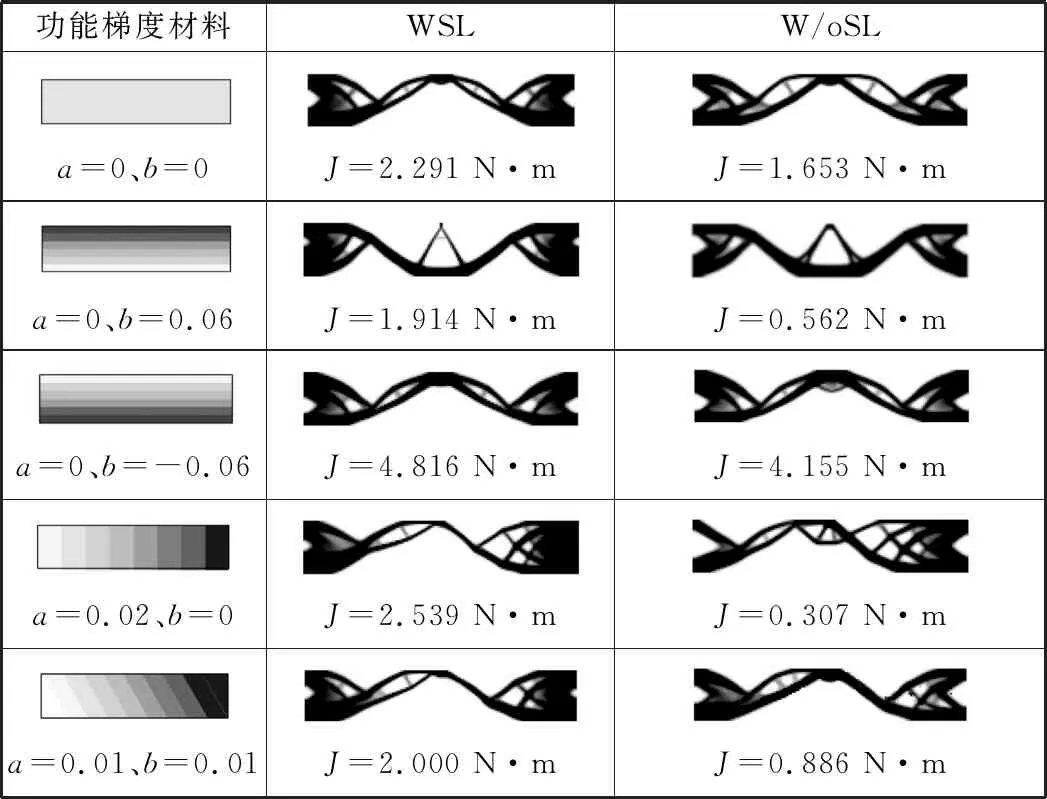
表2 不同二维功能梯度材料结构的优化结果对比

(1)当a=0、b=0时，二维功能梯度材料是均一材料。WSL和W/oSL的优化目标函数值分别为2.291 N·m和1.653 N·m，两者目标函数比值为1.39。

(2)当a=0、b=0.06时，材料密度从下往上递增且每层相同，FGM梯度方向与载荷施加方向一致。受FGM梯度方向的影响，优化最终构型的材料分布与均一材料有明显不同，即有大量材料移动到结构下半部分的密度较低区域，以提供更大的结构动刚度。此外，FGM结构WSL和W/oSL的目标函数值分别为1.914 N·m和0.562 N·m，两者目标函数比值为3.41，考虑自重情况下，有更多的材料向两端约束位置分布，以抵抗自重载荷对FGM材料变形的影响。

(3)a=0、b=-0.06时，材料密度从上往下递增且每层相同。材料梯度方向正好与a=0、b=0.06时的情况相反，FGM结构的最优材料分布规律也与之相反，即大量材料移动到结构上部分密度较低区域，以提高结构整体动刚度。WSL和W/oSL的目标函数值相差较小，分别为4.816 N·m和4.155 N·m，但是最终优化构型上有较明显的差异，即为了抵抗自重载荷的影响，前者的材料更多地向两侧约束处移动。

(4)当a=0.02、b=0时，材料性能从左往右递增且每列相同，梯度方向与载荷施加方向垂直，此时FGM结构产生挠度的方向和材料梯度方向垂直。对比WSL和W/oSL，重力载荷会增大FGM结构在垂直梯度方向的挠度，需要更多的材料分布到结构左侧低密度区域以增加整体结构的动刚度；此外，由于FGM材料不对称，最终的拓扑优化构型存在明显的不对称，且WSL的目标函数是W/oSL的8倍左右，说明了材料梯度方向对FGM结构动力学拓扑优化结果具有很大影响。

(5)当a=0.01、b=0.01时，材料性能从左往右递增，梯度方向与载荷施加方向相交45°。此时，FGM结构变形方向与材料梯度方向相交45°，优化结构的材料部分向FGM结构左下角位置分布。同时，材料梯度分布不对称导致最终的优化构型材料分布不对称。

4.3 功能梯度材料三维结构算例

基于二维的FGM材料模型，三维FGM材料模型在z方向(厚度方向)梯度变化的相关设计参数设为q，则三维FGM的弹性模量和密度为

(16)

一个两端固定三维梁结构，在其上表面中心位置施加矩形载荷F0=G，其几何尺寸、边界条件和外载荷如图6所示。初始设计区域的长度、宽度和厚度分别为15 m、3 m和1 m，网格单元个数为150×30×10，最终设计体积为初始设计区域的40%，过滤半径rmin=2.5，结构自重G=1 375 920 N。为了简化问题且不失一般性，这里假设FGM材料模型在厚度方向不发生变化，即q=0。不过，对本文方法进行适当修改，可以很容易解决三个方向都有梯度变化的情况。

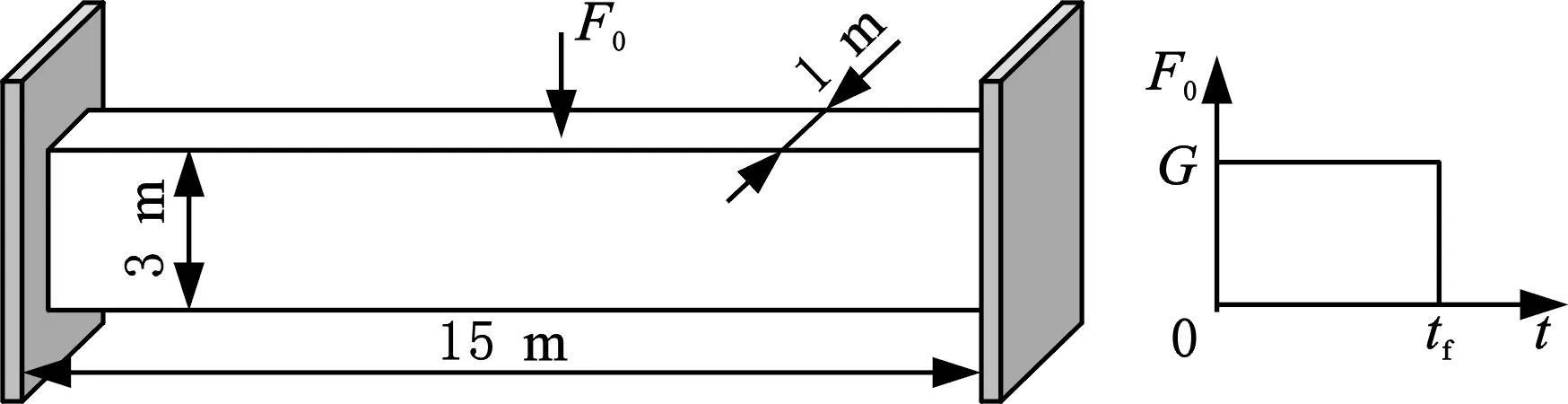
图6 三维两端固定梁结构和外载荷

图7所示为自重载荷作用下，三维FGM结构在加载时间tf=0.1 s、外载荷F0=100%G情况下，不同类型的功能梯度材料的优化结果。可以看出，三维优化结构的边界清晰，优化结果的规律与二维情况类似，表明该方法可以有效应用到三维功能梯度材料结构优化设计中，并进一步验证所提方法的有效性和良好的工程应用潜力。

(a)WSL，F0=100%G，J=5.224 N·m

5 实验与数值仿真研究

5.1 二维悬臂梁结构优化设计

图8 悬臂梁结构初始设计域和边界条件

(a)W/oSL (b)WSL

5.2 悬臂梁结构动力学数值仿真分析

对上述优化结构进行CAD几何重建模，然后利用ABAQUS稳态动力学模块进行动力学仿真分析。采用4节点壳单元(S4)对仿真结构进行网格划分，全局单元网格尺寸为1 mm。图10a和图10b分别表示W/oSL和WSL前4阶模态振型图。注意到，悬臂梁优化结构在oxz平面的弯曲模态时，结构末端点在z方向的挠度最大，因此着重研究在oxz平面的弯曲模态。由图10a可知，W/oSL优化结构的前4阶固有频率分别为129.41，504.33，633.39，715.39 Hz，其oxz平面弯曲模态是第3阶模态，固有频率为633 Hz；由图10b可知，WSL优化结构的前4阶固有频率分别为152.94，558.25，728.56，768.95 Hz，其oxz平面弯曲模态是第4阶模态，固有频率为769 Hz。可见，WSL优化结构的每阶固有频率均有所提高，特别地，在工程中提高结构的第1阶固有频率可以在一定程度上避免结构发生共振。

(a)W/oSL

5.3 动力学测试实验设置

动力学测试实验系统如图11所示，包括数据采集分析仪(型号AVANT-MI-6008)、功率放大器(型号HEA-200C)、激振器(型号JZK-10)、力传感器(型号PCB-208C02)和加速度传感器(型号KISTLER-8776A50M3)；实验平台采用欧标3030铝型材进行搭建；实验样品采用三维打印机(型号JGMAKER-A6)制备，所用材料为PLA，打印层分辨力为0.1 mm，打印方向平行于结构的长度(图12)。

图11 实验装置

(a)W/oSL优化结构

5.4 实验与数值仿真结果对比分析

由上述数值仿真结果可知，W/oSL优化结构的oxz平面弯曲模态为第3阶模态，固有频率为633 Hz；WSL优化结构的oxz平面弯曲模态为第4阶模态，固有频率为769 Hz。为了激发悬臂梁结构在oxz平面的弯曲共振，对W/oSL和WSL优化结构分别施加频率为633 Hz和769 Hz、幅值均为0.42 N的正弦激励。图13和图14所示为W/oSL和WSL优化结构的实验和数值仿真对比结果。图15从实验上对比了WSL和W/oSL优化结构的位移响应。

(a)加速度-时间曲线

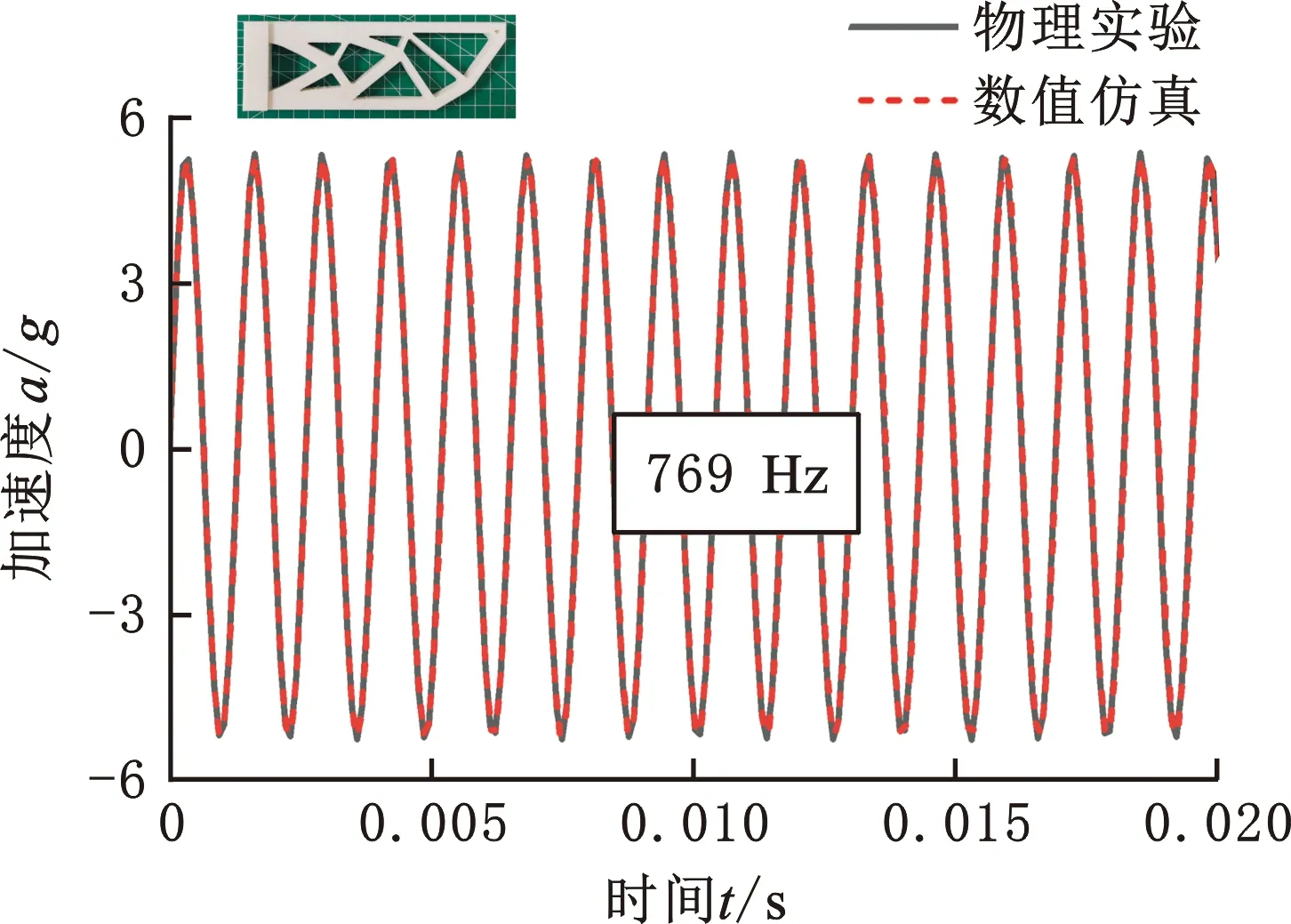
(a)加速度-时间曲线

图15 WSL和W/oSL优化结构的位移-时间曲线实验结果对比

可以发现，W/oSL优化结构的实验和数值仿真的加速度幅值均为7.1g左右，而WSL优化结构均为5.3g左右。此外，两种方法得到的位移幅值都十分相近(W/oSL为0.0039 mm和0.0045 mm；WSL为0.0021 mm和0.0022 mm)，表明实验结果和仿真结果具有良好的一致性。通过实验对比WSL和W/oSL优化结构的位移可以发现，WSL比W/oSL的位移幅值减小了近46%，说明本文所提方法得到的WSL结构具有更大的动刚度。这些结果均证实了所提方法的有效性。

6 结论

本文提出了一种含自重载荷的功能梯度材料结构时域动力学拓扑优化方法，系统研究了自重载荷和材料梯度方向对动力学拓扑优化设计结果的影响，并用实验和数值方法验证了所提方法的有效性。研究发现：①自重载荷和材料梯度分布形式对FGM结构的拓扑优化构型和动刚度具有较大的影响，且为了抵抗自重载荷对FGM结构变形的影响，拓扑优化构型的材料分布会向材料低密度区域移动；②考虑自重载荷的拓扑优化设计可以提高结构固有频率和结构动刚度，在实际工程服役中具有更高的可靠度。需要指出的是，实际工程机械结构会受到不同的载荷激励，针对不同的具体载荷激励特征进行拓扑优化设计和分析十分有必要，笔者将在后续工作中进一步解决该问题。