聚焦问题结构 揭示数学本质

【摘 要】 数学习题课是数学教学中不可或缺的环节，是对概念或定理法则等知识的巩固和深化．在数学习题课中重视开展变式教学，有助于促进学生的数学思考和对学习的迁移，形成完善的知识与方法体系．研究以一道数学中考题为例，以变式教学理论为指导开展初中数学习题课教学，探讨变式的过程和策略．【关键词】 变式教学；初中数学；习题课

2021年7月13日，第14届国际数学教育大会在上海举行，华东师范大学顾泠沅教授受邀作主题为《45年：一项数学教改实验》的大会报告，向国际同行介绍了基于“青浦实验”的数学教育变式理论．所谓变式是指教师在教学中有目的有计划地变换材料的形式，对命题进行适当的转化，在变换过程中探究不变的规律和性质，从而掌握数学对象的本质属性.顾泠沅教授及其研究团队将变式教学分为概念性变式和过程性变式两类［1-4］，其中过程性变式主要聚焦于数学活动和问题解决的有层次地推进，从而构建起联系紧密有逻辑的数学知识体系．

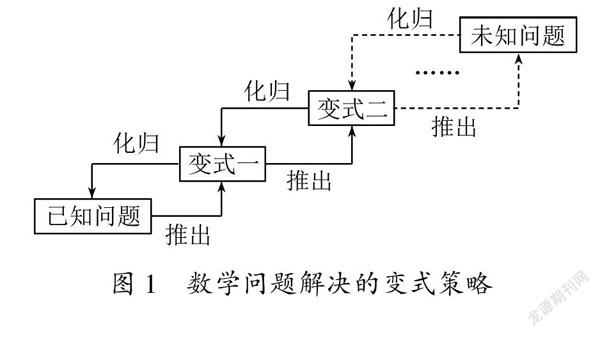
文［4］提出了数学问题解决的思路，指出基本路径与策略是从一般到特殊、化未知为已知、化繁为简，通过一步步的化归变式不断向已知的、熟悉的问题靠拢；在深入解决某个问题后可通过特殊到一般、类比联想等方式变换问题，对问题进行拓展延伸，而要解决新的问题又回到了前面所说的化归思想，如图1．

运用变式教学理论，教师可以更好地开展习题课的有效教学，并启发引导学生对问题展开探究讨论，在解决问题的过程中“学会数学地思考”．下面以一道中考题为例，探讨如何运用变式教学理论指导数学习题课教学，并将师生的教学活动与教师的教研活动有机融为一体．

1 试题呈现

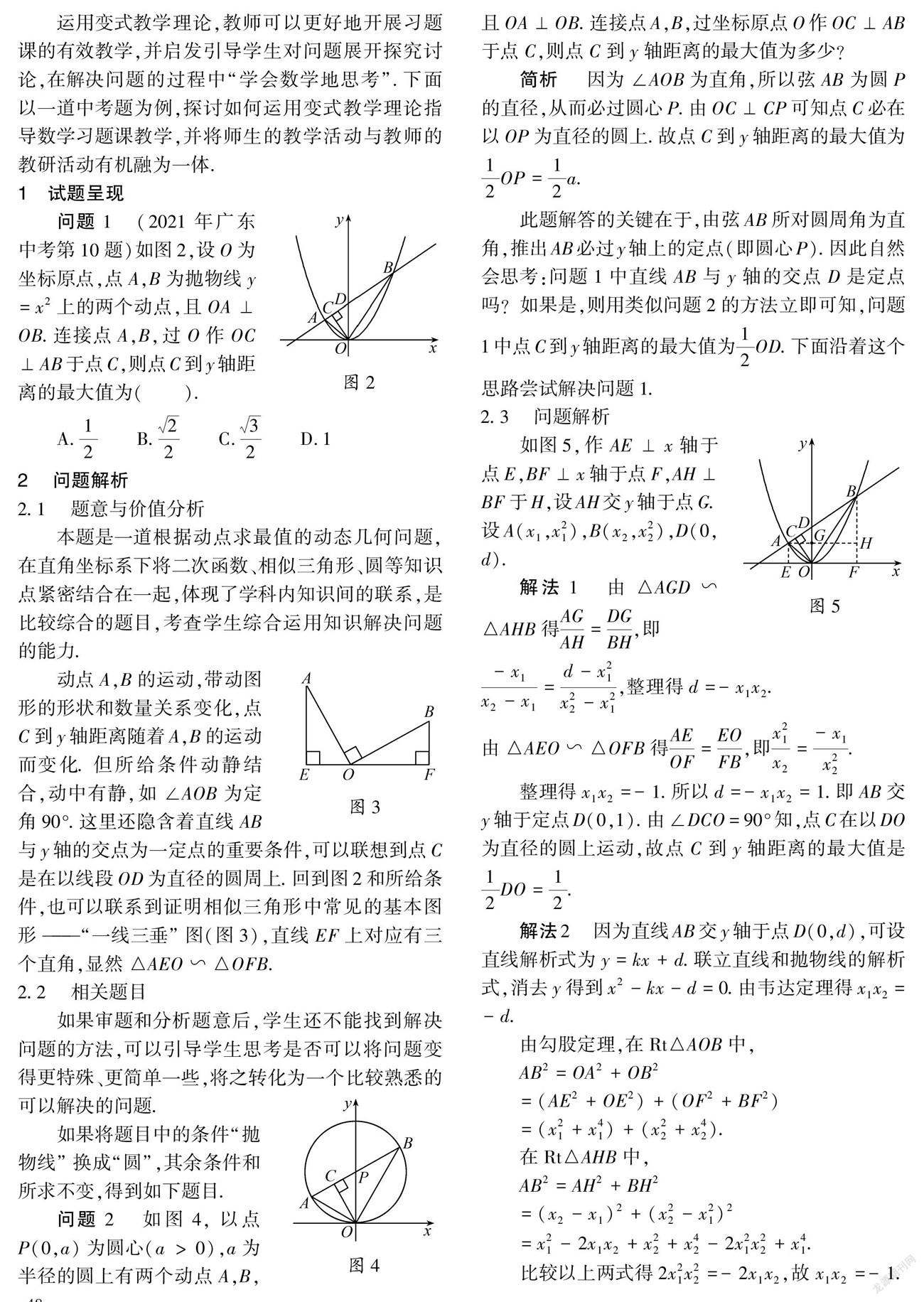
问题1 （2021年广东中考第10题）如图2，设O为坐标原点，点A，B为抛物线y=x2上的两个动点，且OA⊥OB．连接点A，B，过O作OC⊥AB于点C，则点C到y轴距离的最大值为（  ）．

A．12  B．22  C．32  D．1

2 问题解析

2.1 题意与价值分析

本题是一道根据动点求最值的动态几何问题，在直角坐标系下将二次函数、相似三角形、圆等知识点紧密结合在一起，体现了学科内知识间的联系，是比较综合的题目，考查学生综合运用知识解决问题的能力．

动点A，B的运动，带动图形的形状和数量关系变化，点C到y轴距离随着A，B的运动而变化．但所给条件动静结合，动中有静，如∠AOB为定角90°．这里还隐含着直线AB与y轴的交点为一定点的重要条件，可以联想到点C是在以线段OD为直径的圆周上．回到图2和所给条件，也可以联系到证明相似三角形中常见的基本图形——“一线三垂”图（图3），直线EF上对应有三个直角，显然△AEO∽△OFB．2.2 相关题目

如果审题和分析题意后，学生还不能找到解決问题的方法，可以引导学生思考是否可以将问题变得更特殊、更简单一些，将之转化为一个比较熟悉的可以解决的问题.

如果将题目中的条件“抛物线”换成“圆”，其余条件和所求不变，得到如下题目．

问题2 如图4，以点P（0，a）为圆心（a>0），a为半径的圆上有两个动点A，B，且OA⊥OB．连接点A，B，过坐标原点O作OC⊥AB于点C，则点C到y轴距离的最大值为多少？

简析 因为∠AOB为直角，所以弦AB为圆P的直径，从而必过圆心P．由OC⊥CP可知点C必在以OP为直径的圆上．故点C到y轴距离的最大值为12OP=12a．

此题解答的关键在于，由弦AB所对圆周角为直角，推出AB必过y轴上的定点（即圆心P）．因此自然会思考：问题1中直线AB与y轴的交点D是定点吗？如果是，则用类似问题2的方法立即可知，问题1中点C到y轴距离的最大值为12OD．下面沿着这个思路尝试解决问题1．2.3 问题解析

如图5，作AE⊥x轴于 点E，BF⊥x轴于点F，AH⊥BF于H，设AH交y轴于点G．设A（x1，x21），B（x2，x22），D（0，d）．

解法1 由△AGD∽△AHB得AGAH=DGBH，即

－x1x2－x1=d－x21x22－x21，整理得d=－x1x2.

由△AEO∽△OFB得AEOF=EOFB，即

x21x2=－x1x22．

整理得x1x2=－1．所以d=－x1x2=1．即AB交y轴于定点D（0，1）．由∠DCO=90°知，点C在以DO为直径的圆上运动，故点C到y轴距离的最大值是12DO=12.

解法2 因为直线AB交y轴于点D（0，d），可设直线解析式为y=kx+d．联立直线和抛物线的解析式，消去y得到x2－kx－d=0．由韦达定理得x1x2=－d.

由勾股定理，在Rt△AOB中，

AB2=OA2+OB2

=（AE2+OE2）+（OF2+BF2）

=（x21+x41）+（x22+x42）.

在Rt△AHB中，

AB2=AH2+BH2

=（x2－x1）2+（x22－x21）2

=x21－2x1x2+x22+x42－2x21x22+x41.

比较以上两式得2x21x22=－2x1x2，故x1x2=－1.以下同解法1．

两种解法的关键都在于求出点D的坐标，判定其为定点（即不随A，B的运动而变化）．其中解法1中两次运用相似三角形，更侧重于几何直观，而解法2运用勾股定理和韦达定理，更强调代数推理．2.4 方法迁移

得到问题1的解答后，能在别的题目中运用这个结果或者方法吗？可以看到以下这道题也可以运用这个方法完成．

问题3 （2014年四川宜宾市中考第24题）已知抛物线y=x2+bx+c的顶点的坐标为M（0，-1），与x轴交于A，B两点．（图略）

（1）求抛物线的解析式；

（2）判断△MAB的形状，并说明理由；

（3）过原点的任意直线（不与y轴重合）交抛物线于C，D两点，连接MC，MD，试判断MC，MD是否垂直，并说明理由．

3 变式与拓展

3.1 条件一般化

将问题1中的条件一般化，可得如下变式题．

问题4 设O为坐标原点，点A，B为抛物线y=ax2上的两个动点，且OA⊥OB．连接点A，B，过点O作OC⊥AB于点C，则点C到y轴距离的最大值为．

简析 如图5，作AE⊥x轴，BF⊥x轴，AH⊥BF交y轴于点G．设A（x1，ax21），B（x2，ax22），D（0，d）．显然x1≠x2.

由△AGD∽△AHB可得AGAH=DGBH，即

－x1x2－x1=d－ax21ax22－ax21．

化简得d=－ax1x2.

由△AEO∽△OFB得

AEOF=EOFB，即ax21x2=－x1ax22．

化简得a2x1x2=－1．故d=－ax1x2=1a．

因此，点D（0，1a）为定点．又因为∠DCO=90°，所以点C在以DO为直径的圆上运动，从而点C到y轴距离的最大值是12DO=12a.

运用图象的平移，可以设计如下变式．

问题5 设抛物线y=x2－1上有两个动点A（x1，y1），B（x2，y2），点C为抛物线的顶点且CA⊥CB．请用含x1的代数式表示x2，并证明直线AB必经过一定点．

问题6 设抛物线y=x2－2x+1上有两个动点A（x1，y1），B（x2，y2），点C为抛物线的顶点且CA⊥CB．请用含x1的代数式表示x2，并证明直线AB必经过一定点．3.2 获得一般性结论

在解决问题1和问题4的过程中可以得到如下基本结论．

性质1 如图2，设点A（x1，y1），B（x2，y2）为抛物线y=ax2上的两个动点．则以下三个条件等价，即若其中一个条件成立则另外两个条件也成立．

（1）（定角）OA⊥OB．

（2）（定点）直线AB交y轴于定点D（0，1a），即直线AB的方程为y=kx+1a，其中斜率k随点A，B的运动而变化．

（3）（定积）A，B两点的横坐标乘积x1x2为定值－1a2．

简析 由问题4的解答可知，如果（1）成立，则（2）（3）成立．设（2）成立，联立直线和抛物线的方程消去y得ax2－kx－1a=0，则A，B两点的横坐标满足上述一元二次方程，再由根与系数的关系可得x1x2=－1a2，即（3）成立．设（3）成立，则

AB2=（x2－x1）2+（ax22－ax21）2

=x21+2a2+x22+a2x41-2a2+a2x42

=（x21+a2x41）+（x22+a2x42）

=OA2+OB2.

因此由勾股定理的逆定理得（1）成立．这就证明了（1）（2）（3）三个条件等价．

由性质1“定点”与“定角”的关系，立即可得出下面的性质2．

性质2 如图2，设点A，B为抛物线y=ax2上的两个动点，连接AB交y轴于点D（0，b）．则

（1）当b=1a时，∠AOB是直角；

（2）当0

（3）当b>1a时，∠AOB是锐角．

有了性质1和性质2这样的一般性结论，教师就可以根据学生的基础和教学目标灵活地对问题进行变式延伸，从而一步步地由点到面构建知识与方法体系．3.3 应用性质

近年各地中考数学常常出现与性质1相关的动态几何问题，其考查的内容和思想方法本质上没有太大改变，主要体现在图形或条件上的局部变化，可以通过转化与化归、特殊与一般等方式将问题转化为性质1的情形．

问题7 （2022年南宁市中考第26题）如圖2，在平面直角坐标系中，A，B是抛物线y=ax2（a>0）上两个不同的点，其中A在第二象限，B在第一象限．

（1）当直线AB与x轴平行，∠AOB=90°，且AB=2时，求抛物线的解析式和A，B两点的横坐标的乘积．

（2）在（1）所求得的抛物线上，当直线AB与x轴不平行，∠AOB仍为90°时，A，B两点的横坐标的乘积是否为常数？如果是，请给予证明；如果不是，请说明理由．

简析 运用性质1由“定角”推出“定积”．

问题8 （2015年兰州市中考第28题）已知二次函数y=ax2的图象经过点（2，1）．

（1）求该二次函数的解析式；

（2）一次函数y=mx+4的图象与二次函数y=ax2的图象交于A（x1，y1），B（x2，y2）两点．

①当m=32时，求证：△AOB为直角三角形．

②试判断当m≠32时，△AOB的形状，并证明.

（3）根据第（2）问，说出一条你能得到的结论（不要求证明）．

简析 第（2）问可运用性质1由“定点”推出“定角”．第（3）问答案不唯一，可结合性质1和性质2给出．

4 教学建议

《义务教育数学课程标准（2022年版）》［5］指出，数学教学要关注数学的本质、关注通性通法，这意味着初中数学命题将愈加重视对思维过程和探究过程的考查．变式教学有助于促进数学习题课的高效教学，提升学生的数学思维进而提高对学习的迁移能力．

首先，教师要掌握变式教学的基本路径，理解其内在的思想精髓．如图1，变式教学的核心要义是通过化归将未知问题逐次简约，使之与熟悉的基本问题靠拢．或者反过来，从熟悉的基本问题出发，由简到繁，变换条件设置障碍，逐渐指向未知问题．在习题课教学实践中，教师可利用辅助性提问帮助学生完成类比和转化（可参考波利亚的“怎样解题表”［6］），例如，若学生审题后未找到已知和未知之间的直接联系，教师可引导学生寻找一道以前解过的相关题目，利用之前的方法和结果辅助思考当前题目，例如，本文中为解答问题1先解答相关但更简单的问题2．

其次，教师要完善自身知识体系，以扎实学识支撑高水平变式教学．前面的探究中可以发现，为有效开展变式教学，教师需要贯通初中数学与高中数学甚至高等数学的知识体系结构，理解数学研究的基本思维方式和重要的数学思想方法，掌握初等数学命题的一般性结论，做好初高中衔接知识的教授.如此才能高屋建瓴，站在更高的立意和视角审视初中数学内容，在学生的知识范畴内对问题进行灵活变式和拓展引申，有梯度有层次多角度地引导学生进行探究和思考，逐步形成完善的知识与思想方法体系．

最后，需要指出，习题课变式教学不可一味追求变化导致走向繁难的机械训练．文［3］指出，知识和技能的层次性是动态数学活动的重要特征．对数学问题一味求变求难而不注重层次性，将演变为机械训练，与变式教学的宗旨背道而驰．习题课变式教学不必过分强调多做多练，而是要通过精心的教学设计，让学生体会复杂问题与相关基本问题之间的逐层转化，再利用适量的有代表性的题目递变式地开展变式训练，提升学生分步解决问题的能力，形成多层次的知识网络和系统经验．

参考文献

［1］顾泠沅.教学实验论：青浦实验的方法学与教学原理研究［M］．北京：教育科学出版社，1994：101-125，137-138．

［2］顾泠沅，黄荣金，F·马顿．变式教学：促进有效的数学学习的中国方式［A］.范良火，黄毅英，蔡金法，李士铸．华人如何学习数学［C］．南京：江苏教育出版社，2005：247-273．

［3］顾非石，顾泠沅．诠释“中国学习者悖论”的变式教学研究［J］．课程·教材·教法，2016，36（03）：86-91．

［4］鲍建生，黄荣金，易凌峰，等．变式教学研究（续）［J］．数学教学，2003（02）：6-10．

［5］中华人民共和国教育部．义务教育数学课程标准（2022年版）［M］．北京：北京师范大学出版社，2022．

［6］［美］G·波利亚．怎样解题［M］．涂泓，冯承天，译.上海：上海科技教育出版社，2018.

作者简介 林洁容（1989—），女，广东英德人，硕士，中学一级教师，惠州市名班主任工作室主持人;主要从事中学数学教学和德育研究.