“排队问题”教学尝试与拓展

陈方勇 刘静 方佳雯

【摘 要】 《义务教育数学课程标准（2022年版）》将综合与实践作为数学学习的一个重要组成部分，这是初中生积累数学活动经验，发展数学应用意识的重要载体.本文利用数学等式和不等式，结合問题假设，通过列表、逻辑推理、公式演算等数学方法，得出排队问题中关于“等待时间”的一般性结论.尝试在教学过程中融入数学核心素养、展现中华民族文化自信、树立家国情怀等思政内容，帮助中学生树立正确的世界观、人生观和价值观.

【关键词】 综合与实践；排队问题；等待时间；思政教育

0 引言

《义务教育数学课程标准（2022年版）》指出，数学课程要培养的学生核心素养，主要包括：会用数学的眼光观察现实世界；会用数学的思维思考现实世界；会用数学的语言表达现实世界.排队是我们生活中常见的一种行为秩序，自觉排队是个人素质修养和社会文明的体现，例如排队就餐、排队买票、排队核酸检测等.排队现象中“等待时间”的长短是服务机构和服务对象（顾客）都关注的问题.数学家华罗庚曾经说过，“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学.”本文将利用数学的符号和语言，通过列表，构建等式与不等式等方式探讨生活实际问题——排队问题.我们先来看沪科版义务教育教科书（数学，七年级下册，2013年版）中的2个问题.

问题1 某服务机构开设了一个窗口办理业务，并按顾客“先到达，先服务”的方式服务，该窗口每2min服务一名顾客.已知当窗口开始工作时，已经有6位顾客在等待，在窗口开始工作1min后，又有一位“新顾客”到达，且预计以后每5min都有一位“新顾客”到达.

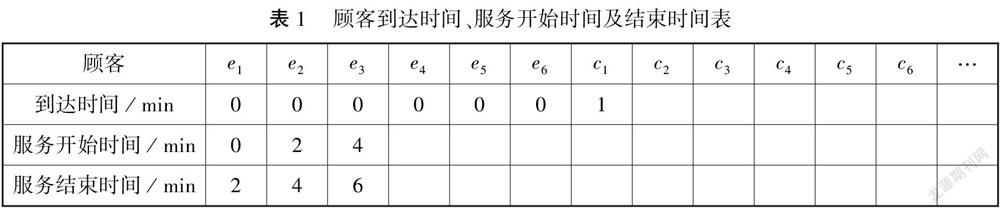
（1）设e1，e2，…，e6表示当窗口开始工作时已经在等待的6位顾客，c1，c2，…，cn表示在窗口开始工作以后，按先后顺序到达的“新顾客”，请将下面表1补充完整（这里假设e1，e2，…，e6的到达时间为0）.

（2）下面表示每一位顾客得到服务之前所需要等待的时间，试将该表2补充完整.

（3）根据上述两个表格，能否知道“新顾客”中，哪一位是第一位到达服务机构而不需要排队的？求出他的到达时间.

（4）在第一位不需要排队的顾客到达之前，该窗口已经服务了多少位顾客？为这些顾客服务共花费了多少时间？

（5）平均等待时间是一个重要的服务质量指标，为考察服务质量，问排队现象消失之前，所有顾客的平均等待时间是多少？

问题2 在问题1的条件中，当服务机构的窗口开始工作时，如果已经有10位顾客在等待（其他条件不变），且当“新顾客”Cn离去时，排队现象就此消失了，即Cn+1为第一位到达后不需要排队的“新顾客”，问：

（1）用关于n的代数式来表示，在第一位不需要排队的“新顾客”Cn+1到达之前，该窗口已经服务了多少位顾客？为这些顾客服务共花费了多长时间？

（2）用关于n的代数式来表示Cn+1的到达时间.

（3）根据（1）和（2）得到的代数式以及它们的数量关系，求n+1的值.

李庆银［1］对以上两个问题进行了探究，借助字母，利用几个变量之间的关系，虽然得到核心不等式：第n人服务结束时间≤第（n+1）人到达时间，但是没有进行深层次的分析与推广.本文将从实际背景出发，通过抽象问题具体化、具体问题一般化、一般问题系统化三个递进过程对排队问题进行分析并推广，以期对同学们后续课程学习、数学方法指导方面提供必要的帮助.

1 抽象问题具体化

排队问题实际背景虽然来源于生活实践，但是假设条件多，具体时间概念之间关系紧密且抽象复杂.问题1直接通过表格形式利用“抽象问题具体化”方法，让学生对抽象复杂问题有直观的感知，从递推关系中找到彼此的联系，从而降低了题目的难度，简化了解决问题的步骤.表格中可以发现“到达时间”“服务开始时间”“服务结束时间”“等待时间”的具体数值及数量关系，其中“等待时间”=“服务开始时间”-“到达时间”.特别地，因为窗口每2min服务一位顾客，而每5min才有一位“新顾客”到达，因此必然会出现窗口服务完某位顾客后等待新顾客到来的情况，并且在第一位无需等待的“幸运”“新顾客”之前，“服务开始时间”=前一个顾客“服务结束时间”，而在这位“幸运”顾客之后，每位顾客“服务开始时间”=“到达时间”.因此，利用表格将抽象问题具体化，理清各个时间概念之间的数量关系是解决问题的关键.

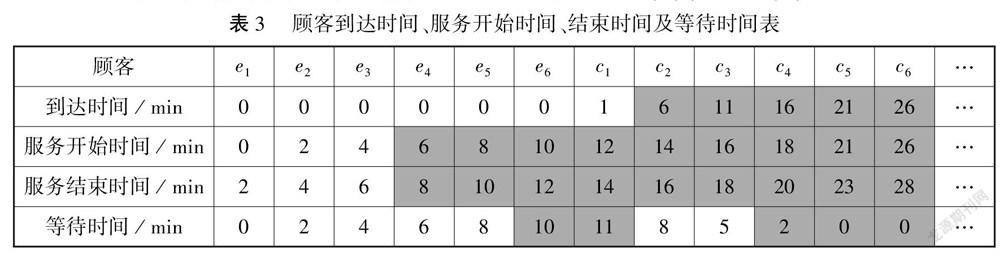
根据以上分析，容易补充（阴影部分）完成表3，解决问题1（1），问题1（2）.

由上述表格，不难得出如下答案：

问题1（3）顾客C5是第一位到达服务机构而不需要排队的顾客，他到达的时间是21min.

问题1（4）在第一位不需要排队的顾客到达之前，即C5之前，窗口已经服务了10位顾客，为这些顾客服务共花费了10×2=20（min）.

问题1（5）所有顾客平均等待的时间是（2+4+6+8+10+11+8+5+2）÷10=5.6（min）.

以上解决问题过程中，通过表格使用“抽象问题具体化”方法，帮助学生理清众多时间之间的数量关系，清晰呈现彼此逻辑关系，可以让一系列困难问题依次迎刃而解.下面将问题进一步深化，将到达时间、结束时间等概念进行字母化、模型化，进入问题2的分析与解决.

在问题2中，当服务机构的窗口开始工作时，已经有10位顾客在等待.于是，第一位不需要排队的“新顾客”Cn+1到达之前，该窗口已经服务了（10+n）位顾客，服务这些顾客共花费2（10+n）min，即顾客Cn服务结束时间是2（10+n）min.根据题设和问题1表格中的结论，不难发现“新顾客”Cn到达时间是（5n－4）min，于是“新顾客”Cn+1到达时间为［5（n+1）－4］=（5n+1）min.Cn+1是第一位不需要排队等待的顾客，说明Cn+1“等待时间”为0，即前一个顾客Cn的服务结束时间2（10+n）小于或等于Cn+1到达时间（5n+1）.通过构建一元一次不等式2（10+n）≤5n+1，解不等式得n≥193.所以n+1≥223，因为n+1为正整数，且Cn+1是第一位不需要排队等待的顾客，所以n+1=8.因此，C8就是第一位到达后不需要排队的“新顾客”，并且之后的每一位“新顾客”都无需排队.

通过以上分析，不难得出问题2的所有答案，在此不作赘述.

2 具体问题一般化

结合问题1，问题2，为了得到更一般性的结论，提出问题3.

问题3 在问题1的条件下，假设当服务机构的窗口开始工作时，已经有m（m是正整数）位顾客在等待（其他条件不变），且当“新顾客”Cn离去时，排队现象就此消失了，即Cn+1为第一位到达不需要排队的“新顾客”，试分析m与n的关系式并求“新顾客”Cn等待的时间t.

分析 由于Cn+1是第一位不需要排队等待的顾客，说明Cn+1到达时间大于或等于其前一个顾客Cn的服务结束时间.又因为Cn+1到达时间是（5n+1）min，Cn的服务结束时间是2（m+n）min.构建二元一次不等式，即为5n+1≥2（m+n），解不等式得，n≥2m-13，因为m，n都是正整数，所以n取大于或等于2m-13的最小正整数，则（n+1）取大于或等于2m+23的最小正整数，Cn+1是第一位不需要排队等待的顾客.

“新顾客”Cn等待的时间t等于Cn服务开始时间与Cn到达时间的差，而Cn服务开始时间等于Cn-1服务结束时间，于是得到方程t=2（m+n－1）－（5n－4），化简得，t=2m－3n+2.显然当等待的时间t>0时，即2m－3n+2>0，解得n<2m+23，即“新顾客”Cn（n是满足n<2m+23的最大正整数）就是最后一位需要排队的顾客；其后一位顾客Cn+1就是第一位不需要排队的顾客.

可以验证问题1中，当m=6时，2m+23=143，即问题1中C5是第一位不需要排队的顾客.

3 一般问题系统化、深刻化

排队问题具有一般性，有必要将零散的认识系统化，将粗浅的认识深刻化、全面化，直到找到问题的本质规律.在具体应用中，必须根据实际问题转换视角，运用逆向思维多角度考察问题.

问题4 在问题1的条件下，假设当服务机构的窗口开始工作时，已经有一群顾客在等待（其他条件不变），且当“新顾客”C10离去时，排队现象就此消失了，即C11为第一位到达不需要排队的“新顾客”，问：（1）窗口开始工作时，等待的一群顾客是多少人？（2）排队现象消失之前，所有顾客的平均等待时间是多少？

分析 采用逆向思维，利用问题3的结论，满足等待时间t>0时的最大正整数n对应的Cn即是最后一位需要排队的“新顾客”；第二个问题不妨设等待的一群顾客（老顾客）是m人，则等待的时间分别是0，2，4，…，2（m－1），所以这m个“老顾客”等待的总时间是m（m－1）；而需要排队的“新顾客”是10人，“新顾客”等待时间分别是t=2m－3n+2，n=1，2，…，10.结论，m个“老顾客”分别等待时间tm=2（m－1），等待的总时间Sm=m（m－1）；n个“新顾客”分别等待时间tn=2m－3n+2，等待的总时间Sn=n（2m－1）+12×（－3）n（n－1），m表示“老顾客”人数，其中n是小于2m+23的最大正整数.

解 设窗口开始工作时，等待的一群顾客是m人.由问题3的结论，Cn等待的时间t=2m－3n+2，令t>0，即2m－3n+2>0，当n=10时，可得m>14，因为C10是最后一位到达需要排队的“新顾客”，所以m应取满足m>14的最小整数，即窗口开始工作时，等待的一群顾客是15人.

由于“老顾客”人数m=15，所以“老顾客”分别等待时间为0，2，4，…，28min，“老顾客”等待的总时间是0+2+4+…+28=210（min）；10位“新顾客”分别等待时间29，26，…，2min，于是“新顾客”等待的总时间是29+26+…+2=155（min）；新老顾客总数是25人，于是排队现象消失之前，所有顾客的平均等待时间是210+15525=14.6（min）.

显然，顾客等待总时间也可直接使用公式计算，“老顾客”等待总时间是S15=15×（15－1）=210（min）；“新顾客”等待总时间为S10=10×（2×15－1）+12×（－3）×10×（10－1）=155（min）.

4 結语

（1）排队是生活中的常见现象，本文通过抽象问题具体化，具体问题一般化，一般问题系统化、深刻化三个过程，以“等待时间”为突破口，通过问题引导，图表制作，分析思考，逻辑推理、公式演算，构建一元一次不等式和二元一次不等式解决实际问题.整个探讨过程情景代入感强烈，不断吸引学生兴趣的同时将排队问题由易到难，由浅到深，逐层分析，使学生对问题更容易认识、理解和掌握.为学生以后学习探究综合与实践问题提供了研究方法与研究方向.

（2）对于排队这一现实生活问题，我们先用数学的眼光去观察它，进而用数学思维去思考分析，最后用数学的语言去表达，达到解决问题的目的.这与新课程标准中数学核心素养的理念相契合.

（3）自觉排队是个人素质修养的体现，中国素有“文明古国，礼仪之邦”之称，中学生更要养成自觉排队的良好习惯.在本节课的教学过程中，教师应当主动引导学生树立正确的世界观、人生观和价值观，积极把思政教育贯穿教育教学全过程.

参考文献

［1］吴之季，苏淳.义务教育教科书数学七年级下册［M］.上海：上海科学技术出版社，2013.

［2］李庆银.排队问题探究［J］.中学生数学，2018（12）：37-38.

作者简介

陈方勇（1981—），男，安徽无为人，本科，中学高级教师;合肥市陈方勇名师工作室领衔人，享受合肥市政府特殊津贴，合肥市学科带头人，合肥市优秀教师;全国初中数学青年教师优秀课二等奖;主要研究初中数学课堂教学;发表20余篇论文.

刘静（1990—），女，安徽合肥人，本科，中学一级教师，区优秀教师，优秀班主任;区课堂教学比赛一等奖;主要研究初中数学教学及数学学科与信息技术融合;发表多篇论文.

方佳雯（1993—），女，安徽桐城人，本科，中学二级教师;主要研究初中数学课堂教学.