分层走班下高中数学C层学生学习能力提升策略

◎冯善司 刘 云

(云南师范大学，云南 昆明 650500)

《普通高中数学课程标准(2017年版)》中指出，数学教育的基本理念是实现人人都能获得良好的数学教育，不同的人在数学上得到不同的发展.自21世纪以来，全球进入经济一体化、信息网络化的时代，一方面，人们享受着经济全球化来到的种种恩惠，另一方面，国家与国家之间展开了对经济、文化、综合国力等的激烈竞争.说到底，这种竞争是对科学技术的竞争.科学技术需要一辈辈人才带着热爱奉献青春、挥洒汗水、刻苦钻研.归根结底，国家与国家之间最大的竞争就是教育的竞争.世界各国的发展都离不开教育事业，我国也不例外.因此，我国非常重视教育事业的发展，教育事业的发展离不开人才的推进，人才的培养也离不开教育与时俱进的新理念与新目标.随着时代的变迁，人们从对解决温饱的渴望到对精神满足的追求，体现着不同时期人们有不同的需求.而我国传统教育模式下的学生千篇一律：一考定终生，甚至有很多只会读书却无法将知识应用到实际中的“书呆子”，已经无法满足新时代背景下国家和党对人才的渴望与需求.考虑到新时代国家与社会的人才需要以及新课标的教学理念，分层走班教学模式是大潮流之趋，是众多教育工作者十分关注的话题.每位同学都是独立的、个性鲜明的个体，尊重学生的差异性，使他们在更适合的班集体里发挥自己最大的可能，最终使学生得到更好的发展是我们每位教育工作者的希望.因此，各地学校纷纷响应国家因材施教的教育方针，结合自己学校的实际情况，开展分层走班教学活动.

一、高中数学分层走班制的概念

高中数学分层走班是指根据一些特定的方面，例如，学生的基础知识、学习能力、学习态度、自主意愿等，将学生分为A、B、C三个层次，将原来的一个行政班级分为A、B、C三个小班，再将三个同层次的小班组成一个数学授课班，其中A班为高级层次班级，B班为中等层次班级，C班为基础层次班级.每个班级并不是固定不变的，每隔一段时间，学校根据学生在这个阶段的表现重新分层，这种流动性可以增强学生的竞争意识，更好地促进教学.教师可根据各个层次学生的学习情况、个性特征设计更加符合学情的教学.虽然有些地方很早就开始进行分层走班教学的试验，但是在一个新的地方，面对不同的学生，可能依然存在很多问题，需要我们去解决.因为C层学生在传统课堂中一直是教师格外关注的群体，因此，本文笔者主要考虑的是C层学生进一步突破自我、提升成绩所面临的主要问题以及解决策略.

二、高中数学分层走班教学模式下C层学生存在的问题

C层学生相比于A、B层的学生，基础较弱，自律性不强，对学好数学没有信心，没有学习的动力，缺乏教师的关注，久而久之，学习的内容越多，越感觉到疲累，他们即使有想要学好的强烈意愿，也很可能心有余而力不足，因此，很可能出现抄他人作业甚至直接抄答案的现象.那么，为何会出现这样的情况呢？主要是由于C层学生学习能力较弱，他们无法达到课堂教学目标的要求.那么，什么是学习能力呢？如何评价一个学生的学习能力的强弱？对于学习能力的定义有很多种说法，不过，我们通常认为学习能力是学习的方法和技巧.爱迪乐教育研究院提出学习能力的六个指标，分别为学习专注力、学习成就感、自信心、思维灵活度、独立性和反思力.本文主要从这六个方面探索，在提升C层学生的学习能力方面提出一点建议和思考.

三、分层走班教学模式下高中数学C层学生学习力提升策略

(一)培养学生的学习兴趣，增强学生的学习专注力

在传统的授课班级中，各个阶段的学生之间差异很大，教师增强学生学习兴趣的策略往往很难实施，并且不能兼顾每个层次的学生.而在分层之后的授课班级中，同一个班级的学生差异较小，可制订符合C层学生特点的教学.C层学生因为基础薄弱，对数学学习没有兴趣，所以往往专注力较差，在一节40分钟的课堂上，很难一直专心听讲，所以，教师需要设计一些吸引学生注意力的环节，提升学生学习数学的专注力.

教师可以利用计算机进行演示，吸引学生的注意.例如，在解决正方体截面问题时，正方体截面是否可以是三角形、四边形、五边形，到截面是否可以为特殊的直角三角形、正六边形等.这其实是一个跨度很大的问题，教师可以用计算机演示，帮助学生观察、理解，这个操作的过程可以引起学生的兴趣和求知欲望.除此之外，根据不同的授课内容，教师可以使用不同的方式吸引学生的注意.例如，教师可以通过穿插数学史、趣味小故事或者做小游戏的形式等来提高学生的专注力.久而久之，学生的专注力提升了，上课时会更少出现分神、注意力不集中的情况.学生上课时认真听讲，课后思考回顾，再加上有困难及时解决，学习能力提升了，成绩自然而然就得到提高了.

(二)设计问题串，增强学生学习的成就感

C层学生由于成绩不理想，在数学学习的过程中获得的成就感、喜悦感很少，在这个过程中，渐渐失去了学好数学的信心.担任C层班级授课的教师，需要更多地关注学生的心理状况，帮助他们减轻学习负担.教师如果将一个对于他们而言较为复杂的问题直接抛出来，他们很难给出想法或思路.教师可以将其拆分成几个较为简单的小问题，以问题串的形式出现，减小题目的难度.即使他们不能答对所有题目，至少觉得自己有更进一步的可能.这时，教师要及时肯定和表扬学生，使他们尝到“成功”和“进步”的滋味.他们在数学学习过程中获得喜悦感和成就感，会更主动地投入数学学习中来.

例如，在“立体几何”这部分内容的复习课上，有这样一道题：

如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面PAD⊥底面ABCD，M是PD的中点，求证：AM⊥平面PCD.

图1

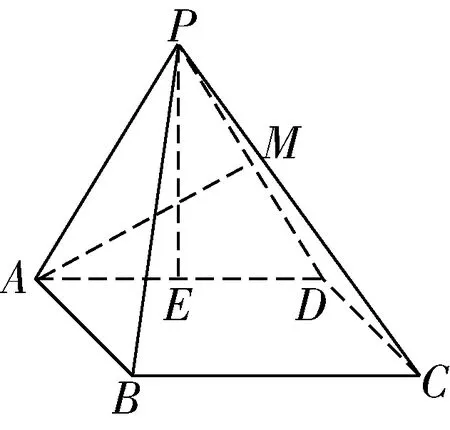
图2

问题1：我们要证明AM⊥平面PCD，有哪些途径？

学生：直线AM垂直于平面PCD内两条相交直线(线面垂直判定定理).

问题2：根据题目中的条件，同学们能够得到什么信息？

学生：根据PAD是正三角形和M是PD的中点可以知道AM⊥PD.

问题3：现在已经找到直线AM与平面PCD内一条直线垂直，只需再找一条线与AM垂直即可.并且我们发现还有一个条件没有用，根据这个条件我们可以得到什么？请试试看找出另一个线面垂直，这个过程中是否需要作辅助线？如果需要，该如何作？

同学们能够根据面面垂直的判定定理和线面垂直的性质定理得到AM⊥CD，那么，这道题就解决了.看似复杂的证明题，在我们一步步的问题突破中找寻出答案.

“问题串”在我们的教学活动中是很常见的，并且是非常实用的，除了在解题过程中用到，在帮助学生更加透彻理解概念、性质、定理时也常用到.

例如，在学习复数的乘、除运算这一节的内容时，得到复数乘法法则：

设z1=a+bi和z2=c+di(a,b,c,d∈R)是任意两个复数，那么，它们的积z1z2=(a+bi)(c+di)=(ac-bd)+(ad+bc)i.

问题4：请同学们观察复数的乘法法则和多项式的乘法法则有什么共性和差异？

学生：两个复数相乘与两个多项式相乘类似，只需要把所得结果中的i2换成-1，再把实部和实部合并，虚部和虚部合并即可.

问题5：当z1和z2都是实数时，两数的乘积是怎样的？

学生：根据复数的概念可以知道，当z1和z2都是实数时，就是z1和z2的虚部都为0，即z1=a，z2=c，那么，z1z2=ac.

教师总结：当z1和z2都是实数时，两复数的积就是实数的积.

问题6：如果z1和z2互为共轭复数，z1z2是什么呢？

学生动手计算：设z1=a+bi，则z2=a-bi，根据复数乘法运算法则得出，z1z2=(a+b)(a-b)=a2-b2i2=a2+b2.

通过这三个问题，学生可以发现，新内容与旧知识之间的联系，它们存在一些相似甚至是相同的规律.教师帮助学生理解、记忆复数的乘法法则的过程，也在帮助学生逐步完善对数学知识体系的认知结构.

(三)关注学生发展，增强学生信心

不同层次的学生，最近发展区也不同，不同的班级教学重难点也应存在差异.对于基础较弱的C层学生而言，教学目标的设计要合理，只要求达到课标的要求，以学习基础知识和基本技能为主要任务，重视教学过程，重在学有所得，注重帮助学生建立学好数学的信心，鼓励他们及时复习，提升动力.例如，在学习复数加减法及其几何意义这部分内容时，只要求他们掌握复数的加减运算法则和加减法运算的几何意义，不需要再进一步拓展加减法几何意义的应用.

除此之外，作为学生学习过程中的引导者，教师应该关注学生甚至还有家长的心理变化.因为分层教学并没有普遍化，特别是在一个学校刚刚开始实施分层走班教学的时候，可能会有一些家长不理解，自然而然地认为C班就是差班，不仅仅是自己孩子的学习成绩稍微差些，理所当然地以为“差班”的教师也差，觉得自己的孩子本来成绩就不好，再在一个全是“差生”的班级里，由一个不怎么样的“差老师”教授，那孩子岂不是越来越差？因此，学校需要安抚学生家长的情绪，与他们做好沟通，讲清楚“分层走班”教学模式的优势，并且每个班级的教师都是一样优秀、一样负责的好老师，孩子在C班并不代表他们是“差生”，只是在现阶段，C层班级的整体氛围更适合他们，对于教师的教授模式，学生更易接受，三种层次的班级教授内容都是完全一样的.得到家长的支持是学校工作开展的重要保障，因此，一定不能忽视家校合作的重要性.学生本身在C层班级，可能觉得自己成绩差被分配到“差班”，从而直接破罐子破摔，更加一蹶不振、没有信心，不利于教学的开展，也不利于学生的发展.在与家长沟通好的前提下，一方面有家长的宽慰，一方面有学校教师的正确引导，使他们正视在C层班级的事实，不要因此气馁，摆正态度，增加动力，增强信心.

(四)注重变式教学，提升思维灵活度

教师总是希望我们的学生可以做一道题就通一类题，甚至做到举一反三，但是仅靠学生自己参悟几乎是不可能的，是需要教师在平时教学中进行培养的.而C层的学生由于基础较弱，学习新内容本来就很慢，要求他们做到触类旁通更是难上加难.因此，教师在日常教学过程中，需要注重变式教学.变式教学指教师利用不同形式的示例、软件与图像资料来解释同一事物的本质属性，或者通过转变同一事物的非本质属性，展现这一事物的科学本质.在这样的学习氛围中，学生提升了思维灵活度，做到理解概念、性质或定理，进而会用它们解决问题，而不是死记硬背做“会”了一道题.

在学习“极值点偏移”这节内容的时候，这节课的内容本来就不是很容易，所以，教师需要带领学生真正理解，不仅仅是让同学们知道它的定义和出题方式，更重要的是真正理解“极值点偏移”的概念，学生只有真正理解，才能在解题过程中以不变应万变.例如，根据定义，可以有以下题目：

已知函数f(x)=xe-x[x∈R，存在x1≠x2，满足f(x1)=f(x2)]，求证：x1+x2>2.

此题可以变式为：

变式1：已知函数f(x)=xe-x[x∈R，存在x1

……

在这个变式训练的过程中，学生真正理解了极值点偏移的概念，见识了不同的题型，提升了思维灵活度.

(五)合理进行作业设计，给学生独立思考的空间

作业是教学活动中不可缺少的内容，高中数学作业可以达到巩固课堂所学的内容和课本知识的目的，学生完成数学作业是他们发展数学思维、培养数学核心素养的重要途径.另外，教师也可以根据作业反馈得出学生近期的学习情况.因此，作业布置并不是教学设计中简单的四个字，而是需要教师经过精雕细磨、精挑细选之后得到的结果.C层学生的作业要符合C层学生的学习情况，围绕着教学目标去设计.机械地重复简单的作业会使学生感到厌烦、疲倦，复杂、困难的作业会使学生丧失信心，很可能导致学生“抄答案”“抄作业”.因此，作业布置要适当、适量，符合C层学生最近发展区，使他们能够努力跳一跳就可以够得着、摸得到.C层学生的作业主要是基础题目，其目的在于学生对基础知识的熟练掌握和对解题步骤的掌握.作业布置也要体现多样性、层次性、创新性和开放性，使学生有兴趣、有能力独立思考去完成它.

学生的学习过程和每一步向前都离不开教师的正确教导.因此，学生完成作业之后，题目的评讲也是非常重要的一环，这一点对于加强学生对知识的掌握和理解的深入是非常重要的，在这个过程中，可以拓展学生的思维方式，引发学生的更多思考.

(六)重视错题纠正，学会自我反思

即使作业是在课标的基础之上，按照C层学生学情来制订的情况下，教师也不敢保证每个学生都会做，那么，我们又如何保障每个学生都能达到教学目标的要求呢？我们可以通过错题纠正，整理错题集，反思回顾.对于作业以及平时测验中出现的错误，学生首先要找到错因，是因为概念不清还是性质不熟，或者是马虎导致计算错误，然后订正写出正确答案.得到题目的解答并简单地把整个过程写下来之后，几乎没有学生会主动回顾和反思这个题目，即使是非常优秀的学生，他们大多数人也是直接投入后面的学习中.回顾和反思可以减少我们在解题过程中出现的错误，帮助我们提升解题能力，是学习过程中不可缺少的重要一环.而这正是绝大多数学生甚至教师都会忽略的部分.因此，我们要重视解题之后的回顾与反思，教师要培养学生总结解题思路和方法的习惯，鼓励学生进行章末总结和错题整理，不断反思，优化自我.

总之，要帮助学生取得更理想的成绩，得到更好的发展，需要提升学生的学习能力.这个过程也并非一朝一夕就可以完成的，需要教师和学生共同努力.教师不仅需要关注学生的外在表现，也需要关注学生的心理发展，帮助学生提升自我.当然，在实行分层走班教学模式的过程中，除了教师和学生的努力之外，还需要学校管理层对制度实施的监督.学校管理层制定严明的分层走班制度，不能徇私作假，保证在教师和学生心中的教育公平.

作者切身参与了一个学期的分层走班的管理和教学，发现分层走班教学模式符合学生的个性差异，给了学生更多的自由选择权，是新时代经济发展的需要，是国家新高考政策下未来教学的趋势.教师在高中数学教学中进行分层走班教学活动，设计更加符合学情的教学，可以提升教学效率，符合学生升学和个性化发展的需要.推行走班制的过程中可能还存在很多问题，有待各位教师及相关部门大胆探索，相信未来分层走班制会越来越完善，学生的学习能力会越来越强.