聚焦数学“深度学习” 回归初函“巧思妙解”——以三角函数的单调性为例

◎沈利芳

(浙江省湖州市菱湖中学，浙江 湖州 313018)

《普通高中数学课程标准》指出，高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质.教学情境是教师积极主动建构知识框架，创设与学习内容相关的、贴近学生实际生活的真实情景和环境.借助数学主题情境，理解数学概念，解读初等“真”函数，以变式“真”问题来驱动，触动学生心灵的“真”教学，是深度教学课堂“真”实践，是培育学生核心素养“真”途径.

笔者有幸开设一节市级公开课，本节课选自人教版2019年高中数学必修第一册(人教A版)第五章“三角函数”第四节“三角函数的图象与性质”，属于专题复习课.笔者从复合函数的角度出发，以单调性为主线，以变式教学的方式，探讨正弦型函数y=Asin(ωx+φ)的单调性，并由此延伸出最值等问题的解法.课堂教学设计新颖独特，受到听课教师的一致好评.笔者在教学反思中无穷回味，并从评课中深受启发，从而整理成文，与广大教师分享.

一、聚焦数学“深度学习”

传统教学重结果轻过程，容易引起学生思维的断层，从而形成“一讲就懂，一听就会，一做就错，一放就忘”的尴尬局面.数学抽象作为数学学科的核心素养之一，笔者在初等函数教学中，特别重视数学概念之间、数量之间、图形之间的关系，并应用变式的转化，使学生感悟抽象的过程.另外，笔者还注重理性思维训练，即学生从事物的具体背景中抽象出一般的规律和结构.

1.初遇三角 精见数“深”

三角函数是初等函数的代表，它与代数、几何、平面向量等有着密切的关联，从而成为全国各地数学高考试卷中的“重头戏”，更是学生的失分点.纵观近两年全国各地数学高考试卷，关于“三角函数”的考查(表1)，从选择题、填空题，到解答题，可谓各路英雄集体亮相，“单调性”“取值范围”“最值”“图象”等八仙过海各显神通，凸显初等函数题的“深”不可测.三角函数作为高频考点，一线教师需要精通其广度与深度.笔者以一道改编题为例，展现三角函数的“深”魅力.

表1 近两年全国各地高考试卷“三角函数”考点统计表

情境一：

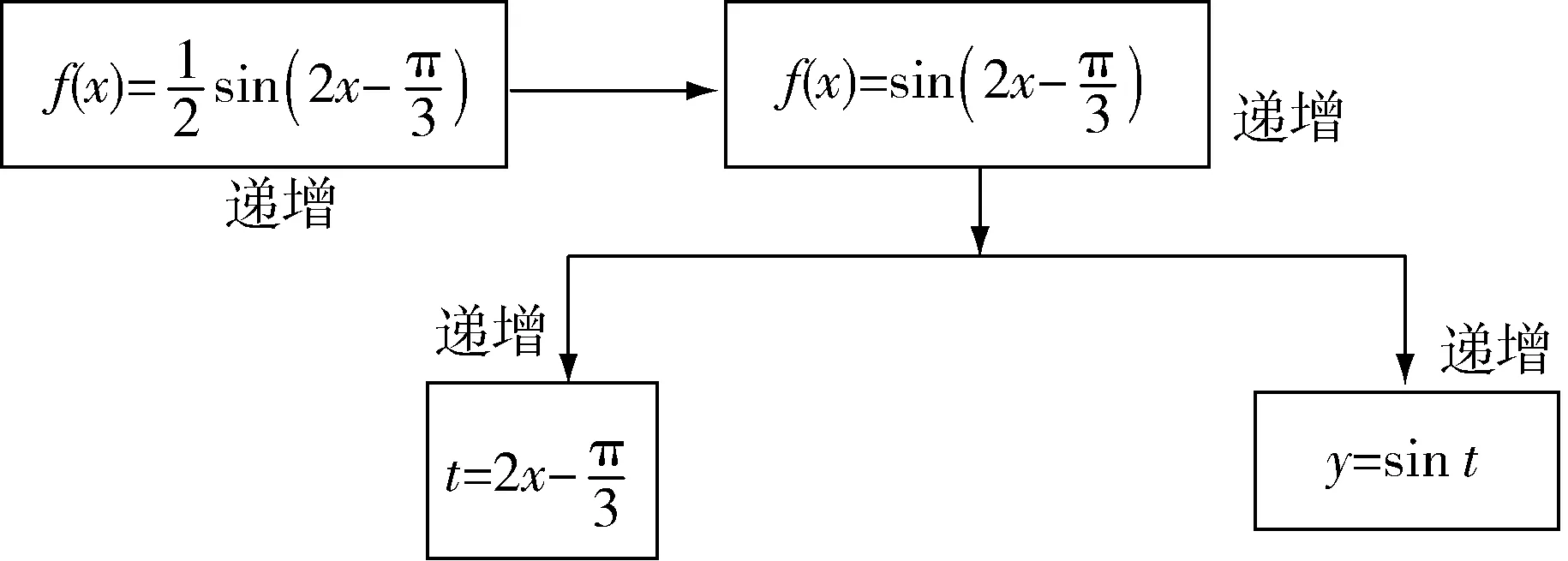
图1 复合函数单调性

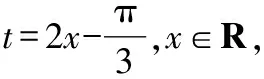
【评注】如果直接以整体换元的方法，将括号内的部分当成一个整体，大多学生就只能生搬硬套，知其然而不知其所以然.而从复合函数的角度加以正确的引导与分析，将其转化为一次函数的单调性和正弦函数的单调性，学生便能利用已学知识理解题目的本质，有一种如鱼得水的感觉.

高中数学的教学评价已从聚焦学生知识能力的掌握，转变为学生核心素养的形成.情境一中关于单调性的有效训练，能提升学生的学习兴趣，并加“深”学生对数学概念的理解，初见数学的学科本质.

2.初变风云 精握数“度”

数学变式教学是项目式学习的一种有效方式，是以某一概念为主题，创设多个情境，设计一连串的问题，从易至难，层层递进，环环相扣，以启发式、悬疑式刺激学生思考维度变化的方法.数学试题风云变幻，教师、学生深陷其中，难以自拔，深感“无解”的痛苦与“有解”的快乐，甚至感觉数学课堂“度”日如年.笔者深度了解学情，精准把握单调性变式的尺度与难度，拨开云雾见天日，柳暗花明又一村.

情境二：

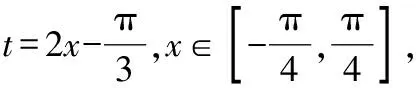
【设计意图】在给定范围内求单调区间，一直是函数单调性求解的难点.一般思路是先求解函数在实数集范围内的单调区间，再与给定区间取交集.但学生对于周期的整数倍等概念感觉比较抽象.因此，在例题基础上限定x的范围，由x的范围得到t的范围，会使学生更容易理解和接受.最值的求解过程也充分体现了函数最值的本质就是单调性.同时，通过最值的求解，学生体会了正弦函数图象的重要性.

变式题，千变的情境，万异的设问.教师跳进题海，学生跳出题海.教师要以学生的“最近发展区”为落脚点，优选典型变式例题，研究数量与图形的关系，提高学生的参与“度”，充分体现学生的主体地位，使其初获数学概念和规则，初成数学方法与思想.

3.初心牢记 精通数“学”

初等函数与生产生活密切相关，是高中数学的精髓所在.但变式不可拘泥于一种题型，要大胆创新，当然也要符合学生的实际需要.笔者牢记数学教学的初心，从数学抽象出发，将例题两次变式，从数量之间的关系到与图形之间的关系，关联单调性与最值，致敬数“学”的独特魅力.

情境三：

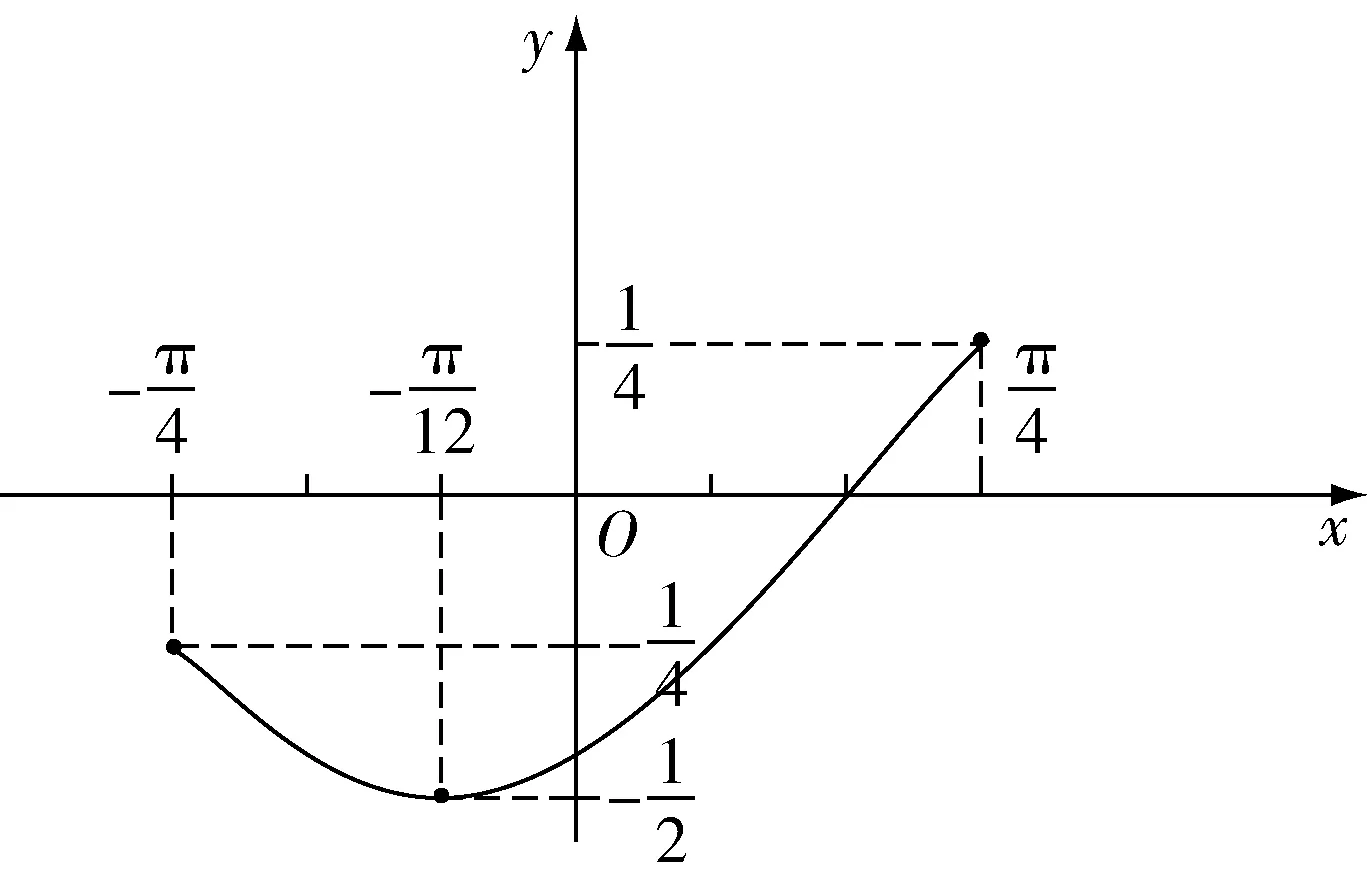
图2 函数图象

【设计意图】如果直接呈现此题，学生会感觉有点突兀，且题目难度有点大.但是，在变式一函数单调区间的基础上，很容易画出函数f(x)在给定区间内的大致图象.教师通过为学生铺设台阶，让他们有一种“跳一跳就能够得到”的感觉，进而达到事半功倍的效果.

从变式一到变式二，变化的情境创设不断激发学生的求知欲.学生不再“似懂非懂”，不再“消化不良”，而是熟能生巧，学会在联想中寻求思路，数学课堂从浅层教学走向深度教学，数学抽象素养不再“抽象”.

4.初出茅庐 精熟数“习”

重要的数学概念、规律、模型等均有一个逐渐形成的过程，学生不可能简单地通过一个情境、一个问题就可以完全理解.为了让学生举一反三，教师需要趁热打铁、乘胜追击，将主题教学进行到底，展开深度探究，从感知图象，到最值，再到取值范围，让学生在思考过程发现真问题，掌握真规律，所谓“学而时习之，不亦说乎”.

情境四：

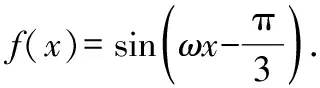
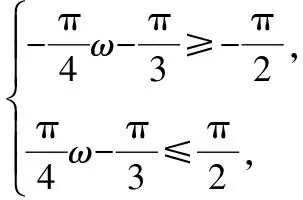
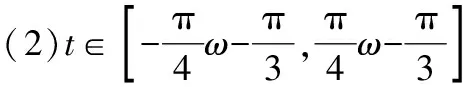
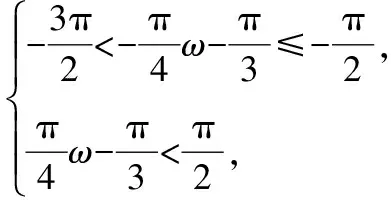
【设计意图】该题的设置与例题中的单调区间、最值相对应，有着画龙点睛、首尾呼应的作用.含参数问题通常具有一定的综合性，如何由繁化简是一大难点.通过例题和多次变式，学生已有将函数分解的经验，因此在面对习题时不会束手无策，能尝试运用例题的解法来求解，并在解答过程中会有一种豁然开朗的感觉，学“习”能力有了质的飞跃.

纵观整节课的教学设计，围绕一个典型例题逐步展开，回归到初等函数y=sinx，分支为三个变式.教学过程中渗透函数思想与数形结合思想，以三角函数的单调性为主线，演变为利用单调性求最值、作图象、探究特定条件下的单调区间问题.学生利用数形结合思想解决最值与交点等综合问题，通过反思—问题生成—探究—解决问题的深度学习过程，培养高阶思维能力.

二、回归初函“巧思妙解”

以单调性为主线，见证三角函数的变式教学，回归到初等函数的图象变化.初等函数的变式教学，其结构往往呈直线递进式，由浅入深，层层铺开，变式内容的设置始终要遵循学生的思维，逐一变化条件，使学生的思维螺旋式上升.在教学中，教师感悟数学概念形成的抽象过程，回归初等函数的优化设计时需要凸显四个方面的教学价值.

1.“巧”用变式，激发学生兴趣点

在备课过程中，教师应该有目标地对例题进行灵活转化，引导学生从三角函数单调性“变”的现象中，探究“不变”的数学本质，在“不变”的本质中发现“变”的规律，进而使学生在有限的变化中领略初等函数概念的无限魅力.变式教学有利于学生积极参与探究过程，能引导学生快乐学习，探索知识的发生、发展的过程，这能极大激发学生的学习兴趣，拓展学生的视野，真正体现学生的主体地位.

2.“思”用变式，激活学生思维点

教师要根据新课标制订教学目标，并结合学情，不断优化变式题.对于数学学科而言，变式教学是一种值得推崇的教学方式，它能够避免教学过程中知识、能力、方法的分裂，能让学生的思维向更宽、更深的方向发展，从而有效提升学生的理性思维能力，培养学生的数学抽象等核心素养.

3.“妙”用变式，突破教学重难点

在“双减”政策的大背景下，学生跳出“题海”的前提却是教师必须要跳入“题海”.教师需要在众多三角函数题中，厘清单调性这条主线，优化教学情境，提炼知识本质，扩充课堂容量，提高课堂效率，达到变式教学的最高境界.教师若能从变化事物的非本质属性中概括出事物的本质属性，则将有助于学生琢磨数学概念之间的前因后果，加深学生对数学知识与方法的深刻理解，从而突破初等函数教学的重点与难点.

4.“解”用变数,击中教学转折点

数学抽象是数学学科的基本思想，贯串于在数学产生、发展、应用的全过程.以三角函数概念为例，它的形成一共经历了六个阶段(表2).从锐角三角函数的概念，到任意角的三角函数概念，到初等函数的概念，概念的内涵不断加深、拓展；从“解”三角形，到三角函数的最值、单调性、奇偶性、图象，从数量关系到空间关系，都需要引入变式教学，实现利用单调性“解”最值到图象的转变，击中每个阶段的转折点，达到本质的飞跃.

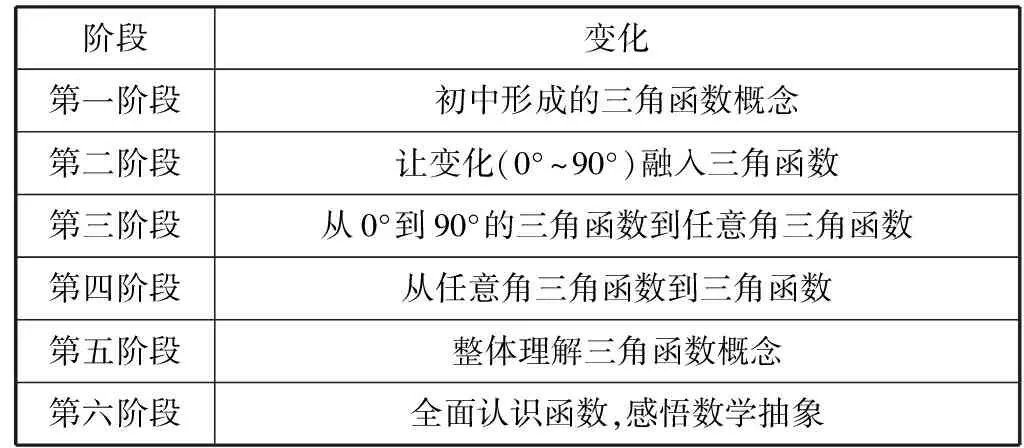
表2 三角函数概念形成的六个阶段

北京大学姜伯驹院士说：“数学已经从幕后走到台前，直接为社会创造价值.”数学学科的重要地位已受到全社会的关注.多解、多变是实施数学深度学习的重要措施.将变式教学深度应用到教学中，不仅可以充分挖掘学生的潜能，让学生对数学思想的认识实现新的飞跃，培养学生的发散性思维、创新意识和创新能力等高阶思维能力，而且可以让学生更全面地透过本质看待数学问题，彰显与众不同的数学课堂的魅力，培养学生的数学抽象等学科核心素养.