非对称来流下总温和壁面粗糙度对矩形转圆隔离段气动热力性能的影响
2022-12-19张堃元
王 渊,张堃元
(1. 广州民航职业技术学院 飞机维修工程学院,广东 广州 510403;2. 南京航空航天大学 能源与动力学院,江苏 南京 210016 )
0 引 言
对于在对称来流下的常规等直截面隔离段,国内外学者主要从流动机理、试验研究、流动控制措施、激波串自激振荡等方面开展了大量的研究[4-8]. Matsuo等在综述文献[9]中将隔离段的研究内容进行了系统性的分类与总结,并将隔离段内激波与附面层相互干扰的流动区域定义为“伪激波区域”(Pseudo-shock Wave Region),该区域主要包含了两部分:分别是存在一系列激波的“激波串区域”和无激波存在的掺混流动 “混合区”. Carroll和Dutton等[10-11]开展了附面层对激波串形态以及隔离段性能影响的实验研究,并用纹影技术观察了激波串的结构. 易仕和等[12]从试验设备分类、隔离段设计、测试方法等方面对隔离段的试验研究进展进行了详细分析,提出了复杂湍流流场的测量试验技术未来发展的一个主要方向是精细流动测试技术. Chung-Jen Tam等[13]采用不同位置的狭缝对隔离段内附面层进行了抽除,发现在隔离段角区抽吸低能流对隔离段性能的提升更大. 曹学斌等[14]开展了在隔离段内设置后掠斜楔涡流发生器的研究,其研究结果表明:在压比不变的情况下,放置后掠斜楔可以减少隔离段的长度,较好地提高了隔离段的性能. He等[15]研究表明,当反压增加时,激波串可以稳定在放气槽后缘,隔离段抗反压能力提高12%只需要损失1.88% 的气体流量,同时还可以减少激波串的压力波动. 苏纬仪等[16]利用周期性的压力对激波串运动的关联性进行了研究,发现出口压力脉动幅值是影响激波串特性的主要因素. 黄河峡[17]开展了复杂背景激波系干扰下隔离段内流动特征的研究,并提出了采用气动斜坡抑制激波串低频振荡流动的控制方法.
高超声速飞行器前体的压缩面一般都比较长,而唇罩一侧经由唇口发展的附面层厚度较薄,导致自由来流在进口截面形成的上下壁面附面层厚度有明显差异[18-19],在隔离段内部形成比较复杂的流动干扰,因此,研究隔离段内部流动时,进口流动非对称这个重要因素不容忽视. 传统的矩形出口截面的进气道结构简单,便于模块化设计,适合安装在采用一体化设计的高超飞行器上,圆形燃烧室的特点是重量较轻,冷却的浸润面积小,利于热防护,并且对于发动机减阻有着较大的优势,因此,为了满足超燃冲压发动机模块化设计以及兼顾圆形燃烧室的优点,开展矩形进口转圆形出口隔离段的设计研究具有一定的工程实际意义. 由于高超声速飞行器飞行过程中受到空气的剧烈摩擦,存在着气动加热的现象,使得飞行时来流的总温会升高[20]. 冷、热两种环境下隔离段的性能存在差异,因此,有必要去探究高焓来流对隔离段内流场的影响. 另外,为了改善高温环境下超燃冲压发动机的性能,延长其工作寿命,应该采用热防护材料对隔离段等结构部件进行防护,但不同的热防护结构材料的表面粗糙度存在着明显的差异,加上隔离段内部经过高温烧蚀后内壁面光滑度下降明显[21-22]. 因此,开展壁面粗糙度对隔离段流场机理影响的研究是十分必要的.
针对以上问题,本文利用数值模拟方法在非对称来流下,探讨气流总温及壁面粗糙度等因素对沿程截面变化的隔离段气动热力性能的影响.
1 数值计算模型及方法
1.1 矩形转圆隔离段模型设计
超椭圆曲线是通过变化其指数的范围进而扩展成的一族封闭曲线,它的特点是对称性强、变换过渡性好,具有较优的控制性[23-24]. 针对矩形进口转圆形出口隔离段设计的需求,本文采用基于超椭圆曲线的设计方法:首先保持轴向中心线不变,进出口之间利用超椭圆曲线指数变化得到通用截面型线,角区收缩引起的截面损失通过沿程当量扩张角来补偿. 该设计方法实现了沿程截面变化可控,由矩形进口截面渐变过渡为圆形出口截面.
基于超椭圆曲线的矩形转圆隔离段方程在极坐标下的表达式为
z=Rcosθ,
(1)
y=Rsinθ,
CFG桩、桩间土以及褥垫层共同组成刚性复合地基。由于CFG桩桩体自身刚度大,可以使荷载从桩顶向桩底部传递过程中有很大的可调性,所以与一般柔性桩复合地基相比,地基承载力大幅度提高。此外,CFG桩复合地基在充分发挥桩承载力的同时,桩可以沿着整个桩长发挥侧摩阻力和端摩阻力,使得桩间土一起参与受荷工作,能够大幅增加承载力并减少沉降。CFG桩复合地基广泛应用于处理各种地基加固中[4-5],包括黏性土、粉土、砂土和自重固结已完成的素填土等地基的处理。
(2)
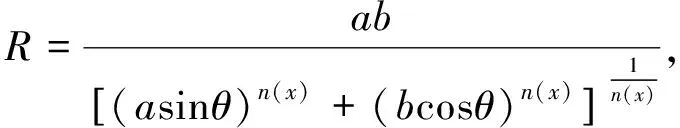
(3)
式中:a,b,n(x) 均为大于零的实数.
根据超椭圆指数n(x)的变化来实现不同截面型面,其表达式为
n(x)=(nx=1-nx=0)×y(x)+nx=0,
(4)
(1-x)+y(x)=1.
(5)
另外,本文使用了沿程截面宽高比控制参数AR(x),通过截面宽高比控制参数来实现沿程截面的宽高比变化可控,其表达式为
AR(x)=(ARx=1-ARx=0)×Y(x)+ARx=0,
(6)
(1-x)+Y(x)=1.
(7)
最后,利用数值积分计算得到截面面积
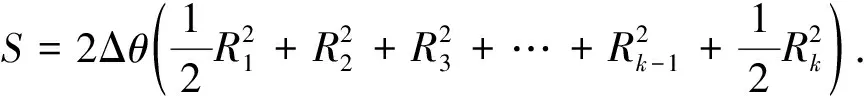
(8)
合理选取以上参数进行隔离段设计的程序编写,得到了基于超椭圆曲线沿程截面渐变的矩形转圆隔离段,其中隔离段模型的尺寸为:进口截面为30 mm×30 mm 的矩形,长高比为10,沿程当量扩张角为0.2°,出口截面是半径为17.9 mm的圆,具体如图1 所示.

图1 基于超椭圆曲线矩形转圆隔离段Fig.1 Rectangular-to-circular isolator based on hyperelliptic curve
1.2 数值计算方法
采用Fluent软件进行数值模拟,湍流模型采用k-ωSST模型,采用二阶迎风格式离散方程,时间推进采用隐式算法,并对计算域网格采用了局部加密措施以适应粘性计算和激波捕获的需要,确保近壁面y+约为1左右. 整个计算域网格总数为138万左右,分子黏性系数使用 Sutherland 公式来计算,比热容采用温度的多项表达式,其各项系数取自美国JANAF热力学函数表. 计算中使用了压力远场、压力出口和绝热无滑移固体边界条件. 为了校核数值方法的可靠性,本文对文献[4] 的实验结果进行了算例验证,图2 给出了隔离段侧壁面对称线的沿程压力数值结果与实验数据的对比,其中数值结果与实验数据较为吻合,因此,该数值方法具有较高的可信度.
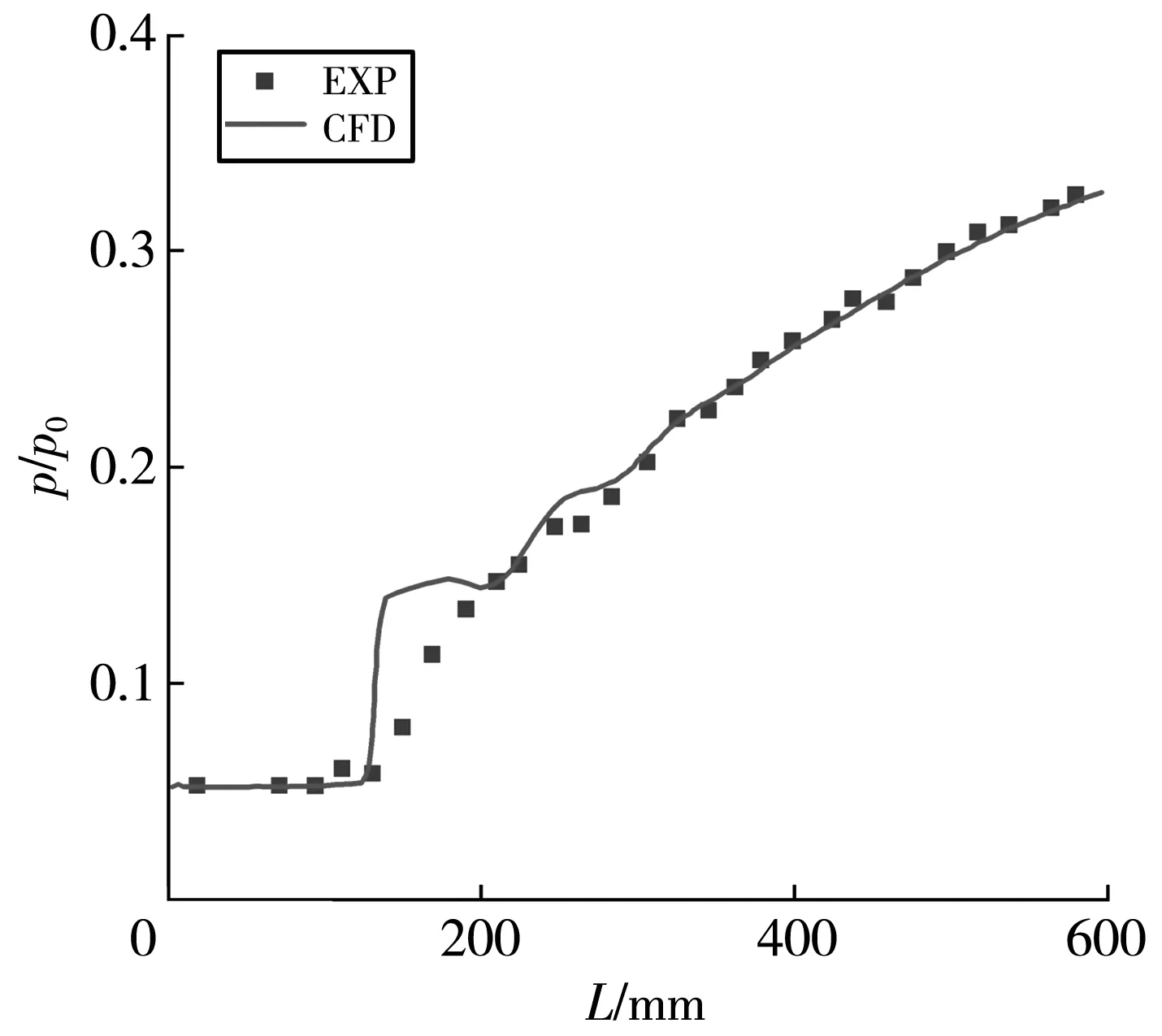
图2 隔离段侧壁面对称线沿程压力数值结果与实验数据的对比Fig.2 Comparison between experimental and CFD results of sidewall pressure
1.3 非对称进口气动布局
在实际的超燃冲压发动机工作时,自由来流流过飞行器的前体压缩面后,在隔离段入口其流动呈现严重的非对称畸变的特点,会对隔离段内部流动产生复杂的干扰. 因此,数值模拟时需要考虑进行非对称进口流动的气动布局.
本文利用附面层发展段形成上下对称并具有一定厚度附面层的流动状态,然后通过附面层排移槽将隔离段进口上壁面的附面层排出,形成进口附面层上薄下厚的非对称来流气动布局,即隔离段入口处的上壁面没有附面层. 计算区域主要包含附面层发展段、附面层排移槽和矩形转圆隔离段三个部分. 附面层发展段的长度为 250 mm,高度为36 mm,附面层排移槽与流场对称轴(沿流向)的夹角为10°,矩形转圆隔离段的长度为 300 mm. 由于模型和计算区域呈现对称化特点,采用流场的1/2进行数值仿真(如图3 所示).

图3 流场计算区域Fig.3 The flow field calculation area
2 计算结果与讨论
2.1 来流总温对矩形转圆隔离段的影响
在非对称来流条件下开展了高焓高马赫数的矩形转圆隔离段数值模拟,数值计算时保持来流马赫数Ma=2.2,来流总压p0=3.65×105Pa, 隔离段出口反压pe=1.194×105Pa等边界条件不变,一共选取了三种工况进行仿真,来流总温T的取值分别为300 K,450 K和600 K.
图4 给出了不同的来流总温下隔离段对称面的马赫数云图. 由图4 可以看出:随着进口来流总温的提高,隔离段内激波串的初始位置不断前移,同时激波串长度在增长,说明高焓来流降低了隔离段的抗逆压力梯度的能力. 当来流总温比较低(T=300 K)时,隔离段内初始激波为λ激波形态. 由于初始激波与隔离段下壁面的附面层相互干扰,使得附面层发生转捩,低能气流发生了分离,形成了涡流区,导致隔离段下壁面低能流迅速发展,并将激波串整体结构整体往上抬升;而对比T=450 K与T=600 K两种工况,随着来流总温的增高,在隔离段进口处的上壁面附面层干扰下,入射激波逐渐增强,对隔离段流场干扰加大,使得初始激波改变为x激波形态,但是激波后造成的分离包与来流总温低时相比变小了,其原因是在来流总温的提高工况下,尽管激波后造成的压升导致其向低速的气流转变,但气流总焓增加能够有效减小激波后近壁处气流的分离. 虽然提高来流总温使得隔离段内的分离区在减小,但是温度的提升使得气体粘性效应增大,加快了沿程附面层发展的程度,使隔离段上壁面附面层逐渐增厚,产生挤压效应,从而使总温较高工况下(T=600 K)的隔离段内激波串结构位置比总温较低的工况(T=300 K)更靠近隔离段中心线,因此,主流区位置由原来比较靠近上壁面逐渐向隔离段流场中间移动,流场非对称效应逐渐减弱,这说明总温提高有助于减缓流场的非对称程度.
本文将三种工况下隔离段沿程上、下壁面对称线的压力进行了对比,结果如图5 所示. 图中,横坐标和纵坐标分别用入口高度和来流总压进行无量纲化. 由图5(a) 可以看出,当来流总温较低时(T=300 K工况下),上壁面对称线的压力曲线波动上升较为剧烈,这是由于隔离段上壁面形成的附面层厚度薄,激波造成的压升和激波后再附过程中膨胀波的减压在亚声速层内无法完全弥散造成的;但随着来流总温的升高,气体粘性效应增加,上壁面附面层迅速增长变厚,因此,这种压力的波动逐渐被近壁的附面层耗散,壁面压力曲线波动幅度逐渐减弱. 由图5(b) 可以看出,隔离段内下壁面对称线的压升趋势是一致的,在初始激波后的静压曲线在前半部分快速上升,在后半部分平缓上升.T=600 K工况下隔离段激波串的初始激波位置相比T=300K工况下的位置向前移动的距离大约为隔离段总长度的17%. 总体而言,由于附面层厚度快速增长,反压向前传得更远,不断将隔离段内的激波串向前推移.
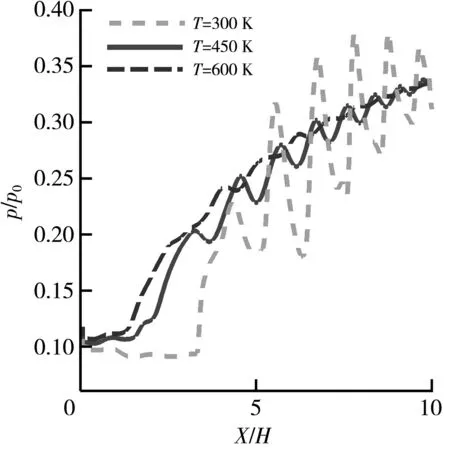
(a) 上壁面对称线的沿程压力分布
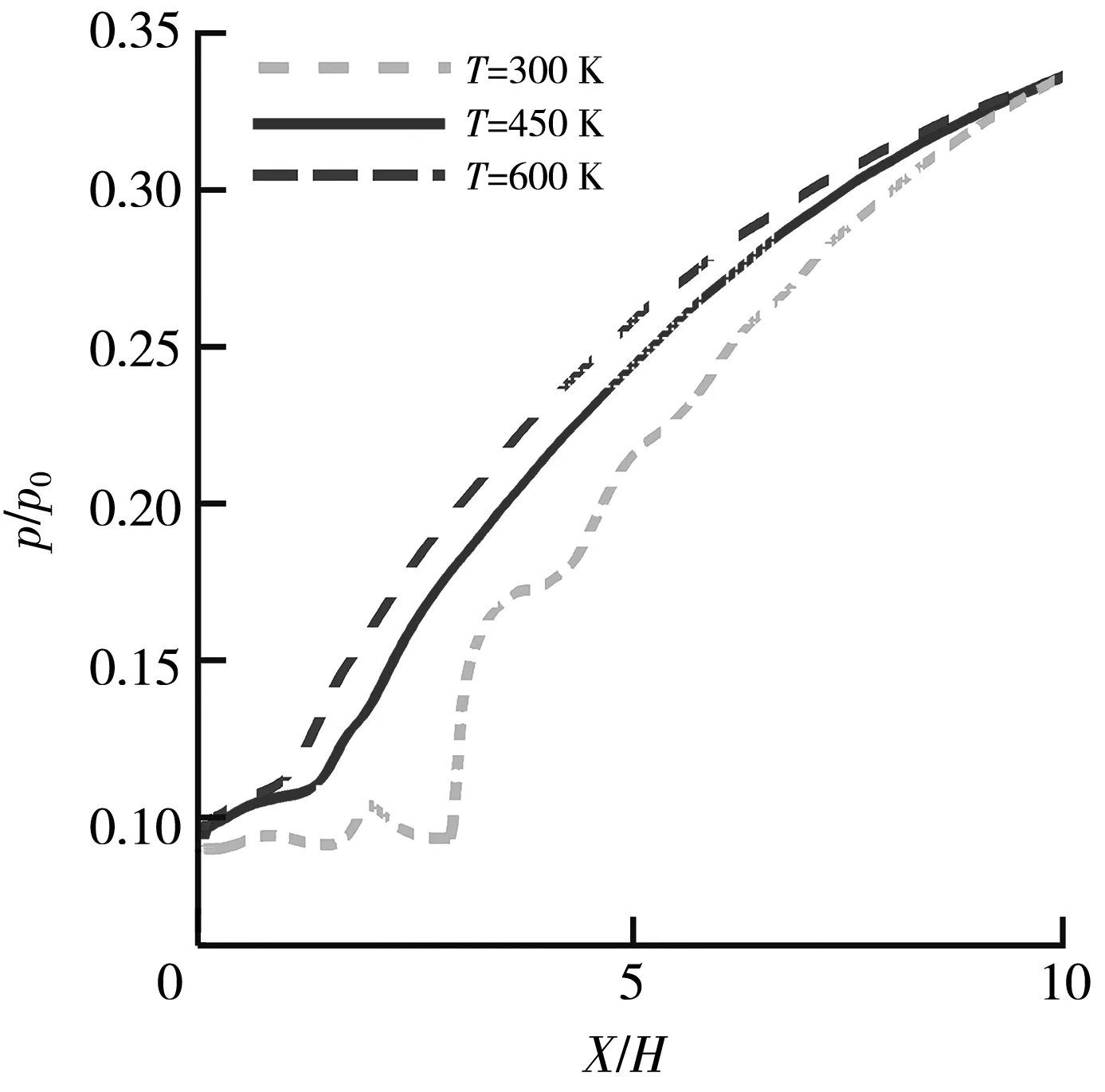
(b) 下壁面对称线的沿程压力分布图5 不同来流总温下隔离段壁面对称线的沿程压力分布Fig.5 Pressure distribution along the wall symmetry line of isolator under different incoming flow total temperatures
图6 为不同来流总温时隔离段出口截面的马赫数云图. 总体而言,随着来流总温的提高,隔离段沿程壁面的附面层迅速发展,上壁面以及两侧壁面的低能流增厚,从而挤压激波串向隔离段流场的中心线靠近,流动三维效应加剧,造成其出口截面流场结构存在差异,但核心区的马赫数却并未受到太大影响. 另外,来流总温的提高使得低能流总焓相对增加,因此,近壁区流动分离状况有所改善,出口流场品质提升.
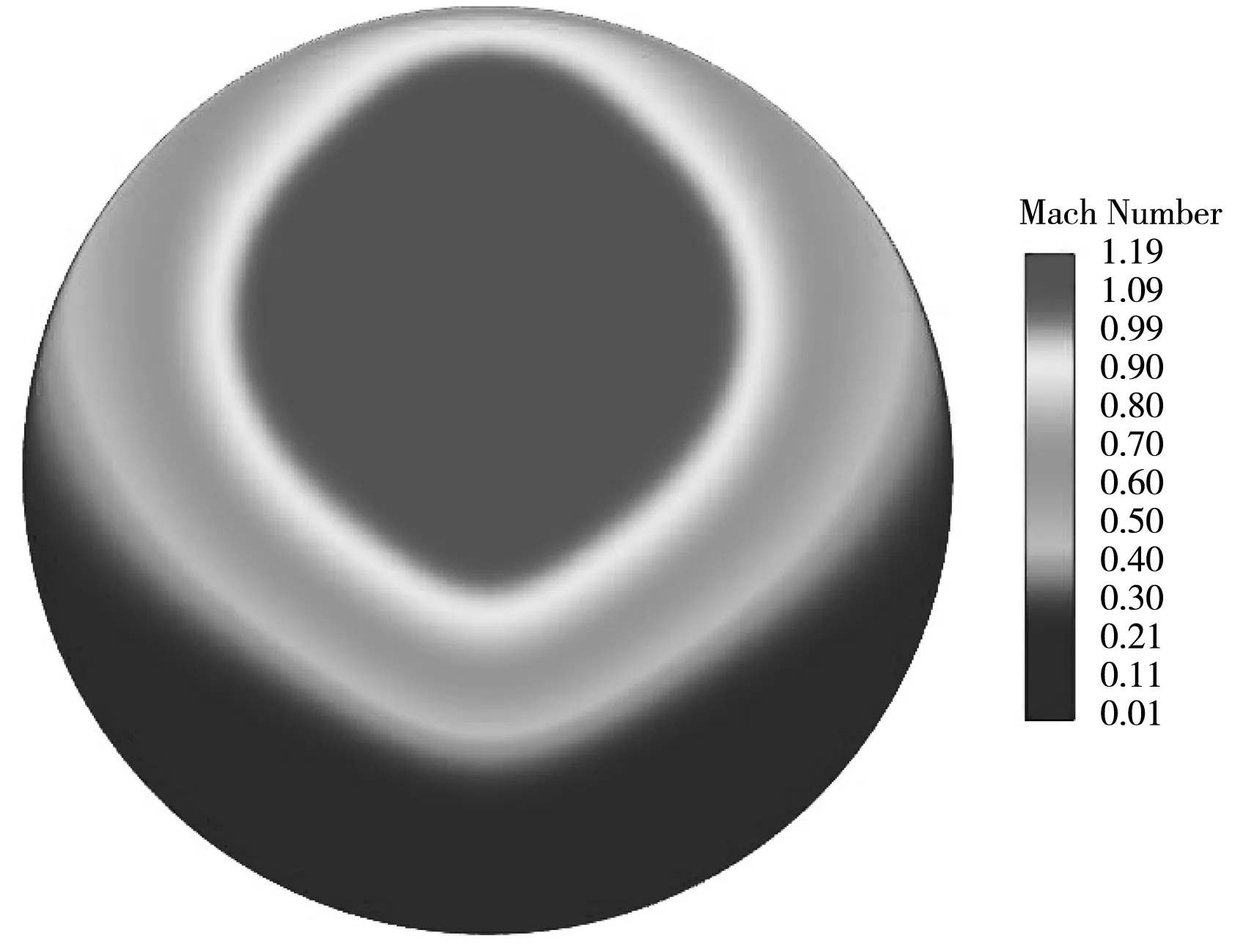
(a) T=300 K
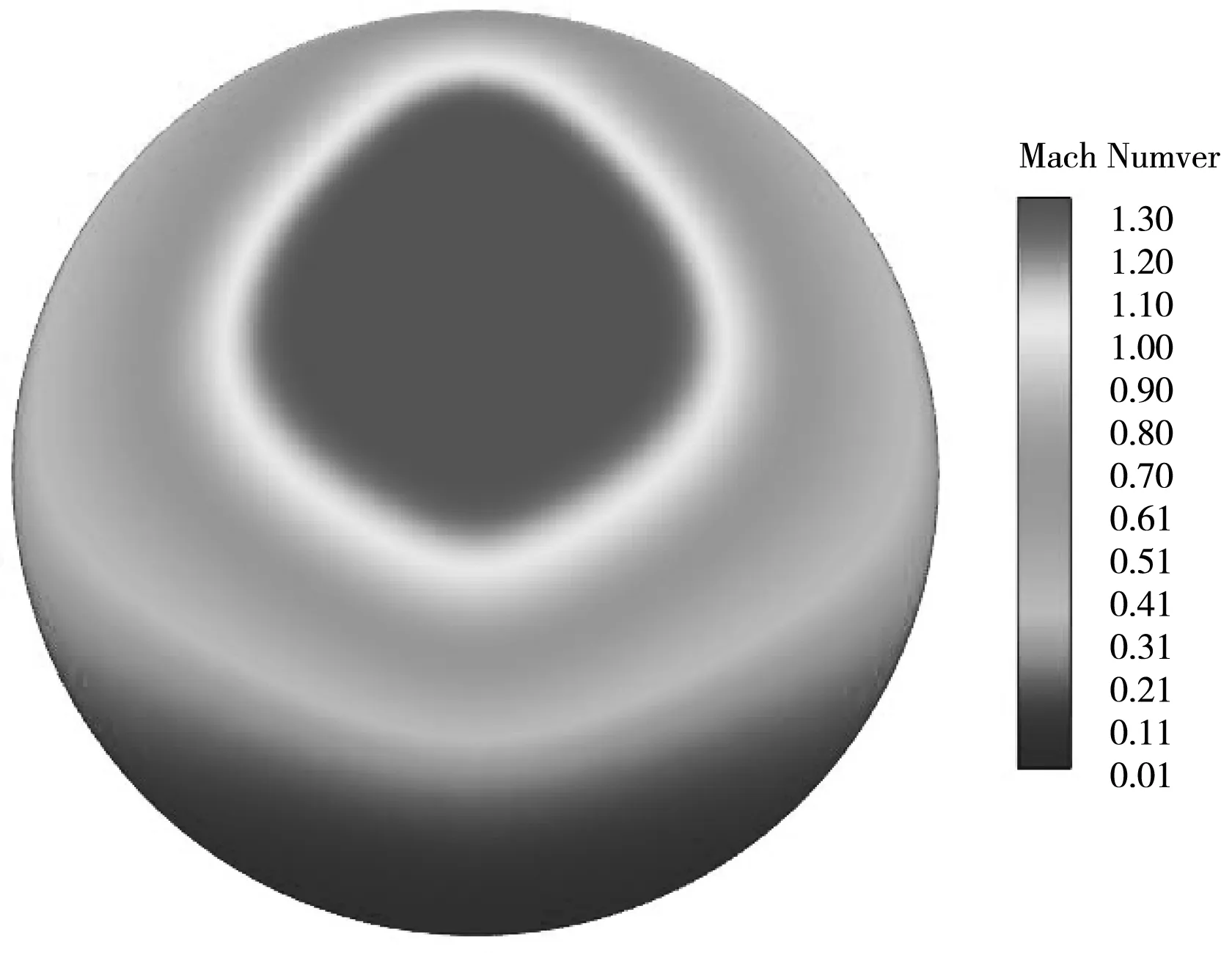
(b) T=450 K
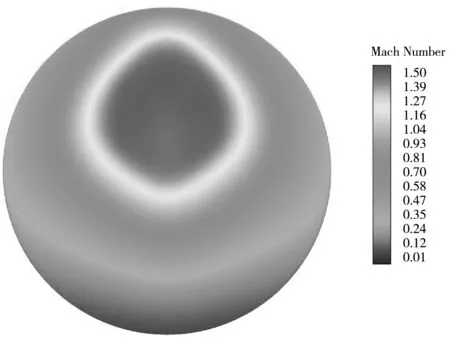
(c) T=600 K图6 不同来流总温下隔离段出口截面的马赫数云图Fig.6 The Mach number contour of the outlet of isolator under different incoming flow total temperatures
隔离段出口总压恢复系数以及出口质量平均马赫数随来流总温的变化关系见表1. 在相同进口总压的条件下,来流总温不断提高时,出口总压恢复系数也一直在增大,T=600 K工况与T=300 K 工况相比,总压恢复系数提高了7.1%. 分析其原因可知,在T=300 K 工况下,激波后导致的涡流区相对工况T=600 K时更大,因此,低能气流在流场内所占的比例增加,附面层分离损失显著增大,导致了隔离段出口总压恢复系数降低得更多;另外,隔离段出口截面质量平均马赫数在来流总温提高时有所增加,这是由于来流总温的提高使得低能流总焓相对增加,近壁区低能流的速度比来流总温低的工况增大了,同时核心区的气流马赫数并未降低,导致了出口截面质量平均马赫数的提高.
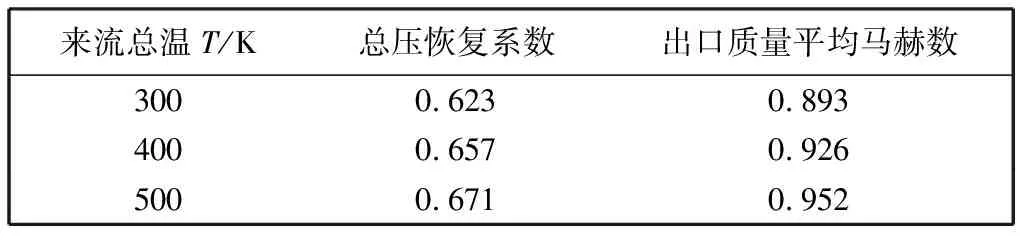
表1 不同来流总温下隔离段性能参数对比Tab.1 Comparison of performance parameters of isolator under different incoming flow total temperatures
2.2 粗糙度对矩形转圆隔离段的影响
本文在非对称来流下对光滑壁面和带粗糙度壁面的矩形转圆隔离段进行了数值模拟,计算时保持来流Ma=2.2,来流总温T=303 K,进口总压p0=3.652×105Pa,隔离段出口反压pe=1.195 39×105Pa. 一般壁面热防护材料的厚度在0.32 mm~0.55 mm范围之内,根据文献[24]选择等效粗糙度粒径法建立粗糙度的物理模型,数值计算时的表面粗糙度为0.014 5 mm.
图7 为两种不同壁面粗糙度的矩形转圆隔离段在非对称来流下的对称面马赫数云图. 由图7 可以看出,两种工况下的隔离段流动状态有所相似,初始激波均为λ激波形态,在下游逆压力梯度的作用下,隔离段内下壁面的低能流发展迅速,使得激波串整体结构偏向上壁面,可知粗糙度未完全改变隔离段内激波串的整体结构形态. 与光滑壁面工况相比,带粗糙度的隔离段内,激波后诱导低能流分离范围更大,附面层沿程的发展相对更厚. 在相同的出口反压下,光滑壁面隔离段内激波串的长度比壁面带粗糙度的隔离段内激波串的长度要短. 分析其原因是在带粗糙度壁面的情况下,由于摩擦系数的增大导致壁面摩擦阻力会稍微增大,造成低速区中气流流速较慢,亚声速层扩张程度相对光滑壁面较大,动量损失厚度增加进而使得附面层厚度增加. 因此,粗糙度的存在降低了隔离段的性能.

图7 两种不同壁面粗糙度隔离段的对称面马赫数云图Fig.7 The Mach number contour of the symmetric section of isolator under two different wall roughness
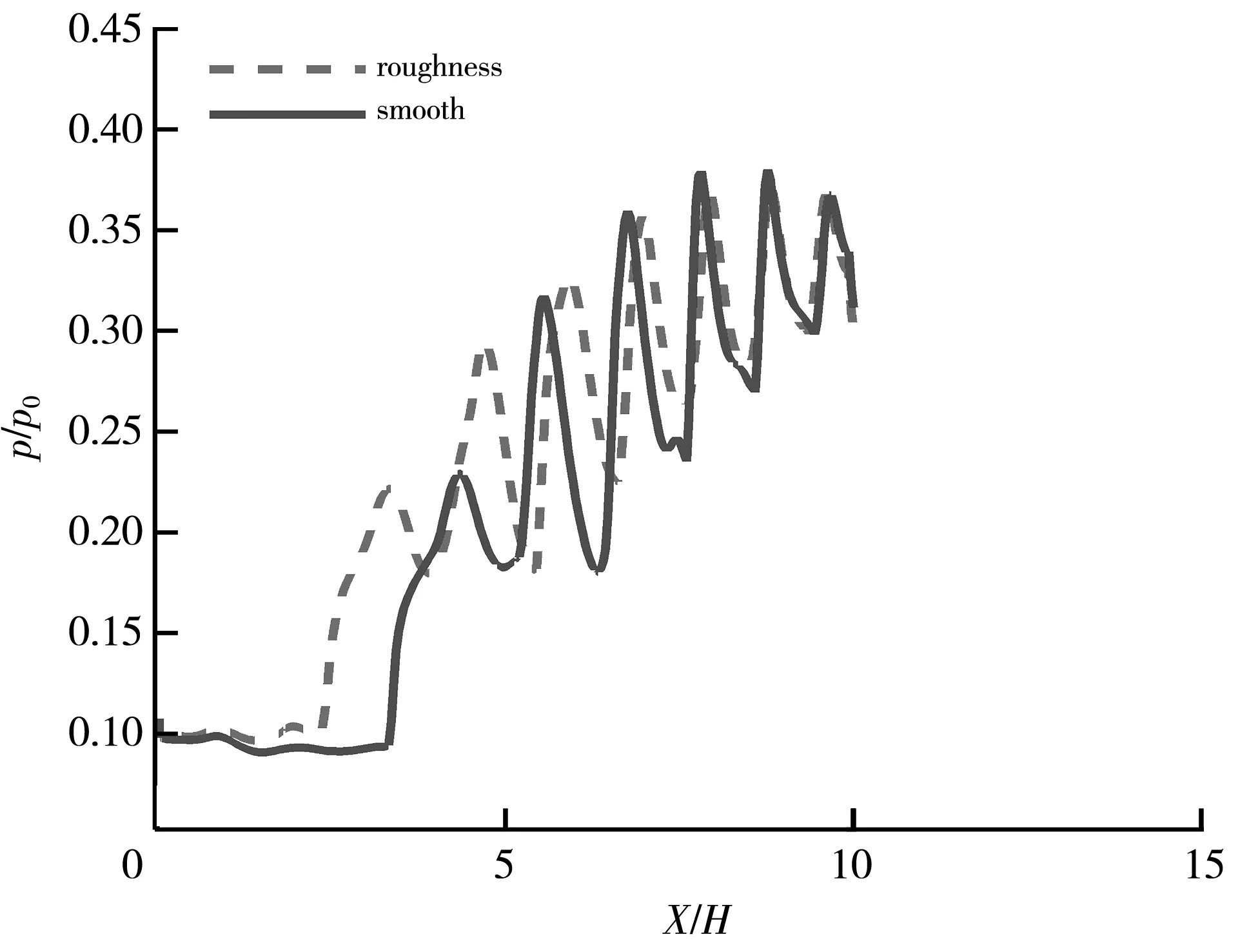
(a) 上壁面对称线的沿程压力曲线
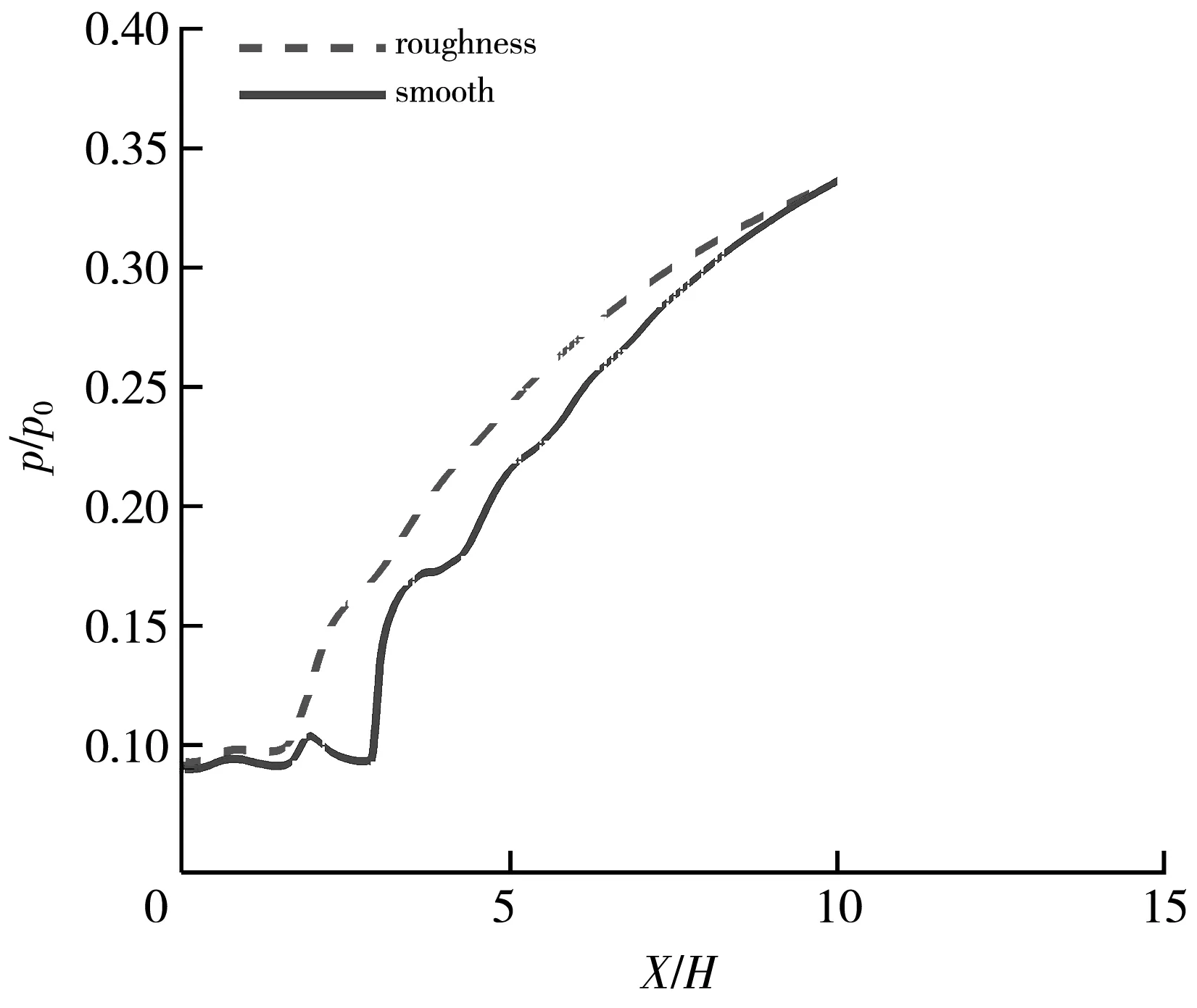
(b) 下壁面对称线的沿程压力曲线图8 两种不同壁面粗糙度的隔离段壁面对称线的沿程压力Fig.8 Pressure distribution along the wall symmetry line of the isolator under two different wall roughness
图8(a) 给出了两种不同壁面粗糙度的隔离段上壁面对称线的沿程压力对比. 其中,横坐标和纵坐标分别用入口高度和来流总压进行无量纲化. 两种工况下隔离段内上壁面对称线的压升规律是类似的,壁面沿程压力均是波动上升,光滑壁面的隔离段沿程压力波动的幅度稍大一些. 图8(b) 给出了下壁面对称线的沿程压力分布,下壁面对称线的压升规律变化趋势也比较类似,在第一道激波之后的压升曲率最大,而后面的壁面沿程压力为平缓上升. 将两种工况下的初始激波位置进行比较,带粗糙度的隔离段激波串的初始激波的位置比光滑壁面工况下的位置向前移动的距离大约为隔离段总长度的9%. 分析其原因,带粗糙度壁面的隔离段内附面层气流受壁面的阻滞相对严重,附面层发展更快,低能气流所占比重增加,必然降低了隔离段的抗反压能力,使得激波串初始位置不断向隔离段入口前移.
图9 给出了两种不同壁面的隔离段三维分离区的对比. 两种工况下上壁面以及下壁面都存在流动分离的情况,而且两者的分离区位置比较相似. 在进口非对称来流条件下,初始激波后隔离段下壁面的流动分离比上面壁面更加严重. 对比两种工况的分离情况,壁面带粗糙度的隔离段内分离区的面积更大,这是由于带粗糙度的隔离段内附面层厚度增长更快,加剧了激波串/附面层的相互干扰,促使隔离段内的分离区进一步扩大.
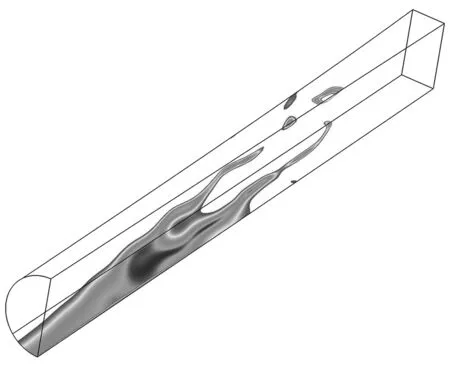
(a) 光滑壁面
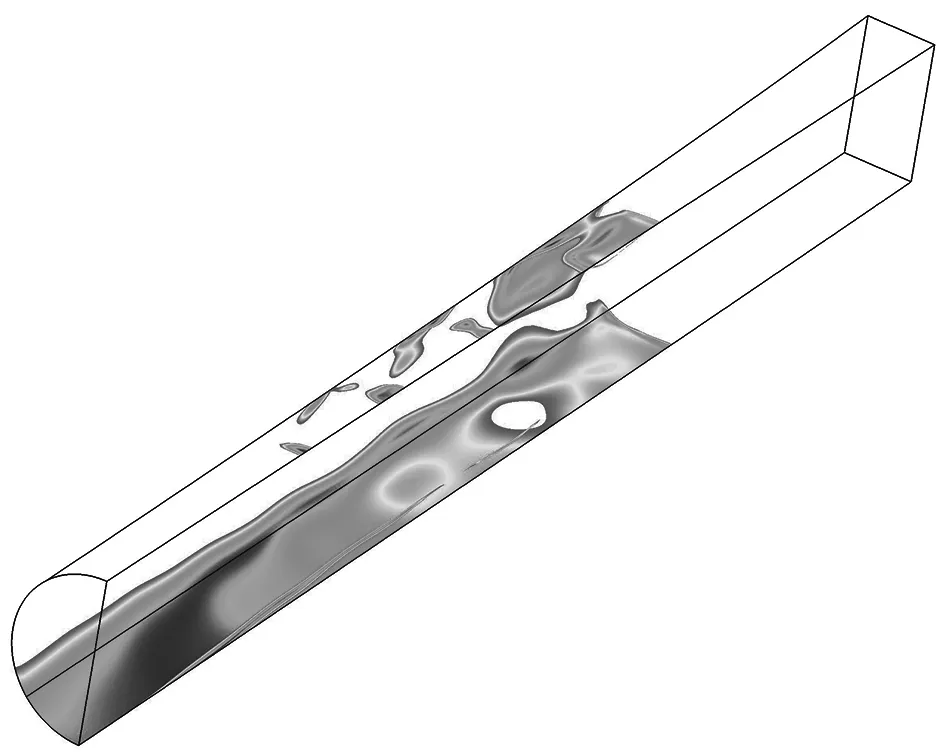
(b) 带粗糙度壁面图9 两种不同壁面粗糙度的隔离段分离区Fig.9 The separation zone of the isolator under two different wall roughness
为了比较两种工况下的出口流场品质,对隔离段出口截面的总压分布进行了分析. 由图10 可以看出,在相同的反压下,主流区较为靠近上壁面,低能流主要集中在隔离段出口截面的下部. 壁面带粗糙度的隔离段出口截面的主流区比光滑壁面的隔离段时的主流区相对较小,因而总压分布均匀度相对更差,造成隔离段出口总压畸变程度增加,隔离段出口流场品质降低.
不同壁面粗糙度的隔离段出口截面性能参数见表2. 由表2 可以看出,相对于光滑壁面的隔离段,带粗糙度的隔离段性能有所降低,总压恢复系数下降了8.3%,并且出口质量平均马赫数下降了6.5%. 分析其原因,带粗糙度的隔离段内附面层发展得更厚,摩擦阻力增加,附面层动量损失厚度增大,导致了出口总压恢复数与出口质量平均马赫数均降低.
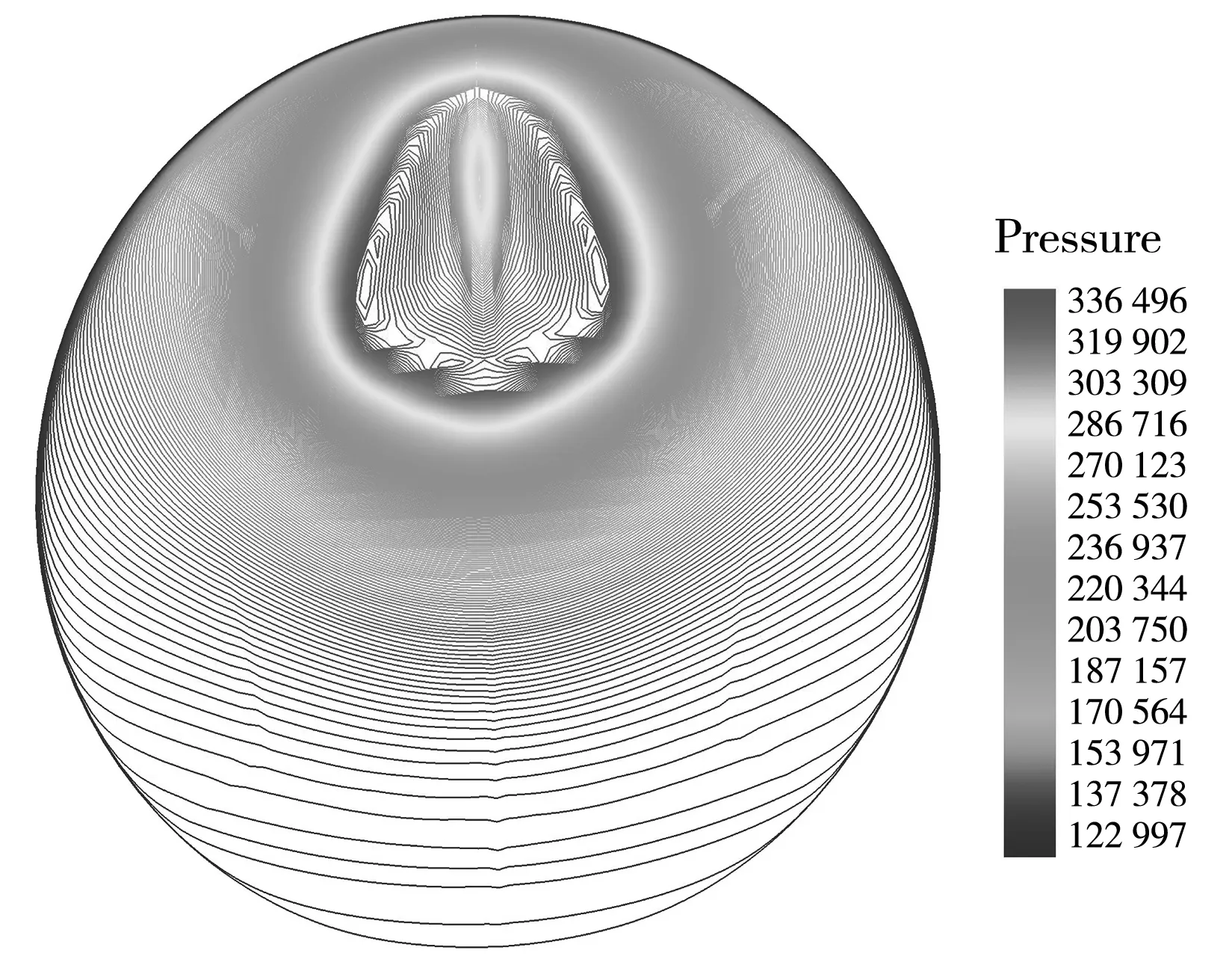
(a) 光滑壁面
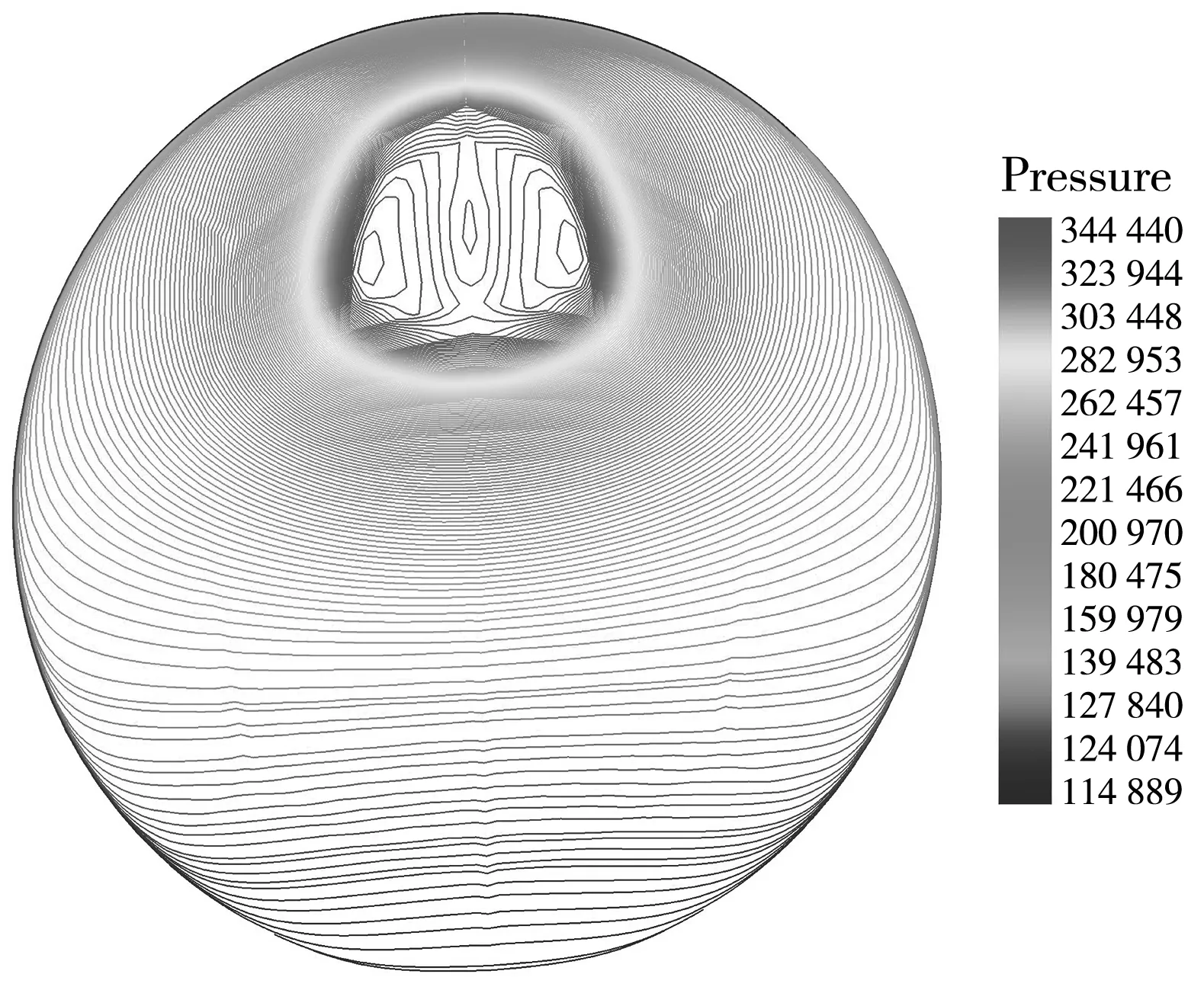
(b) 带粗糙度壁面图10 两种不同壁面粗糙度隔离段出口截面总压的分布Fig.10 The distribution of total pressure at the outlet of isolator under two different wall roughness

表2 两种不同壁面粗糙度的隔离段性能参数对比Tab.2 Comparison of performance parameters of isolator under two different wall roughness
3 结 论
本文采用数值模拟方法开展了非对称来流下不同环境因素对矩形转圆隔离段的影响研究,结果表明:
1) 来流总温的提高能有效改善隔离段内的流动分离,减少低能气流在流场内所占的比例,降低附面层分离损失,提高隔离段出口总压恢复系数;来流总温的增加使得附面层发展迅速,隔离段上壁面附面层逐渐增厚,产生挤压效应,使得主流区往隔离段流场中间移动,流场非对称效应逐渐减弱;
2) 在相同进口总压的条件下,进口来流总温的增加造成隔离段内激波串长度的增长,降低了隔离段的抗逆压力梯度能力;
3) 壁面粗糙度使得摩擦系数增大,造成壁面摩擦阻力增大,导致隔离段抗反压能力下降,并且加剧了激波串/附面层的相互干扰,促使隔离段内的分离区扩大;带粗糙度的隔离段的总压恢复系数、出口质量平均马赫数比光滑壁面的隔离段分别降低了8.3%和6.5%.
