连通图的SDD谱半径及能量的界

姚彦燕，高玉斌

(中北大学 数学学院，山西 太原 030051)

0 引 言

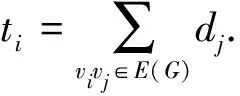
设G的邻接矩阵为A(G)，记A(G)的特征值为λ1≥λ2≥…≥λn，称λ1为G的谱半径.图G的能量定义为

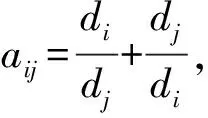
近年来，PAN等[2]得到了最小SDD指数的极图，并确定了n阶化学树的上界；LIU等[3]得到了最小SDD指数的三环图；Ghorbani M等[4]从图的轨道角度研究了SDD指数的一些性质，并得到SDD指数的界；Ali A等[5]等人研究得到SDD指数的下界，并刻画了相应的极图；Zheng L等[6]利用一些不等式研究了AG指数的谱半径和能量的界；Guo X等[7]利用Cauchy-Schwarz等不等式研究了AG指数的谱半径和能量的界. 基于以上研究，本文利用一些基本不等式，得到了图的SDD谱半径和能量的新的上下界，并给出达到这些界的极图.

本文还用到以下拓扑指数：

第一Zagreb指数[9]：

第二Zagreb指数[10]：

遗忘指数[9]：

1 引 理

引理 1[11]设G是n个顶点m条边的连通图，则

等式成立当且仅当G同构于Kn或K1,n-1.

引理 2[12]设G是n阶图，度序列为d1,d2,…,dn，则

当且仅当G是正则图或半正则图等式成立.

引理 3[13]设B=(bi,j)，C=(ci,j)是两个n阶非负实对称矩阵，若B≥C，即对所有i,j，bi,j≥ci,j成立，则ρ1(B)≥ρ1(C)，其中，ρ1(B)，ρ1(C)是矩阵B，C的谱半径.

引理 4[14]若B是一个n×n实对称矩阵，其特征值λ1≥λ2≥…≥λn，则对任意x≠0∈Rn，有

xTBx≤λ1xTx，

等式成立当且仅当x是B对应于最大特征值λ1的特征向量.

引理 5(Cauchy-Schwarz)[15]设ai，bi∈R，i=1,2,…,n，则

2 SDD谱半径的界

定理 1设G是一个n阶连通图，则

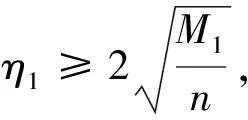
(1)

当且仅当G是正则图等式成立.

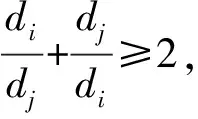
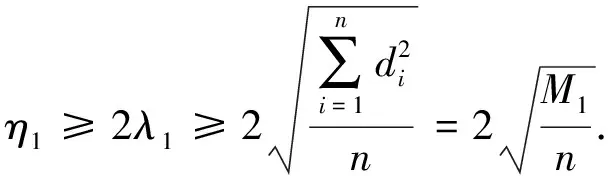
(2)

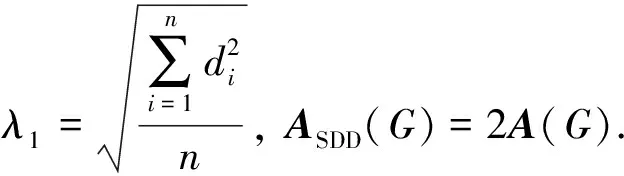
定理 2设G是一个n阶m条边的图，则

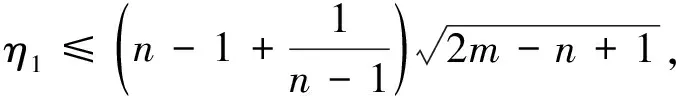
(3)

当且仅当G=K1,n-1等式成立.

(4)

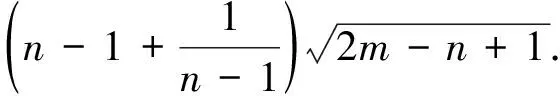
(5)

如果式(3)中等式成立，则式(4)和式(5)变为等式. 由式(4)可知，对任意边vivj∈E(G)有di=1，dj=n-1或dj=1，di=n-1，即G=K1，n-1.

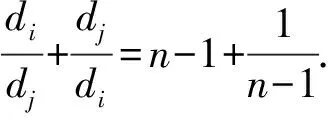
定理 3设G是一个n阶连通图，边数为m，则

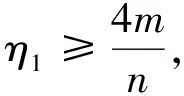
(6)

当且仅当G是一个正则图等式成立.

证明设单位向量x=(x1，x2，…，xn)T∈Rn.由引理4可知

η1(G)≥xTASDD(G)x=

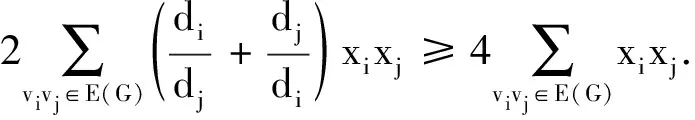
(7)

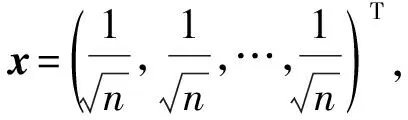
3 SDD能量的界

定理 4设G是一个n阶m条边的图，有最大度Δ，最小度δ≥1，则

(8)

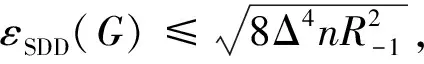
(9)

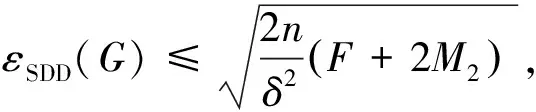
(10)

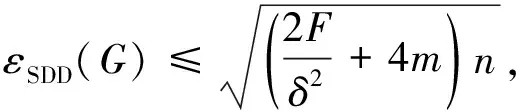
(11)

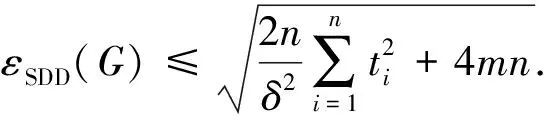
(12)

证明由柯西-施瓦兹不等式得

(13)

因为

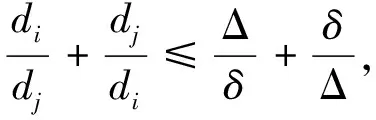
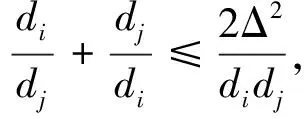
(14)

由式(13)和式(14)可直接得到式(8)～ 式(10).

又由式(13)得

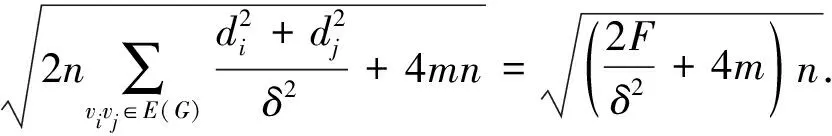
(15)

由式(15)可知

εSDD(G)≤

式(11)和式 (12)得证，证毕.

定理 5设G是一个n个顶点m条边的图，δ>0，则

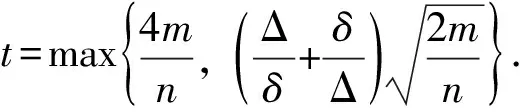
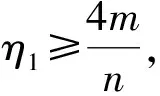
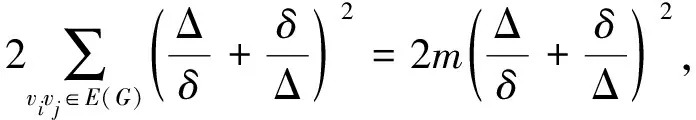
(16)

即

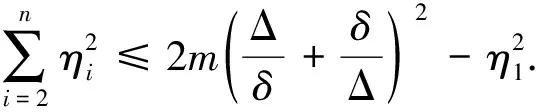
(17)

结合上述不等式及柯西-施瓦兹不等式，得

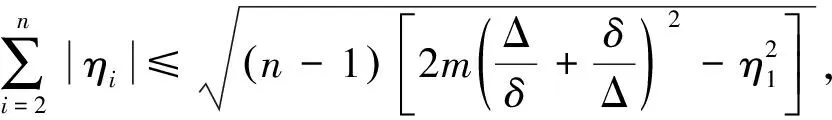
(18)

则

εSDD(G)≤η1+

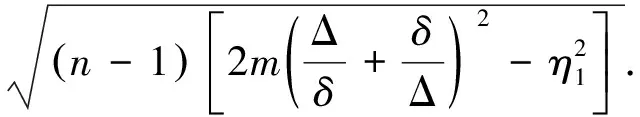
(19)

考虑函数

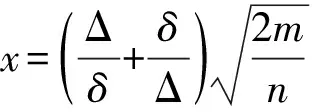
定理 6设G是一个n个顶点m条边的图，且δ>0，则

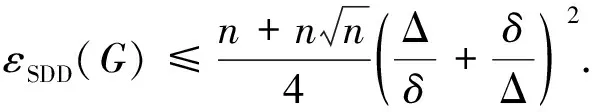
(20)

(21)

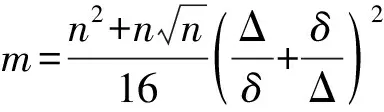
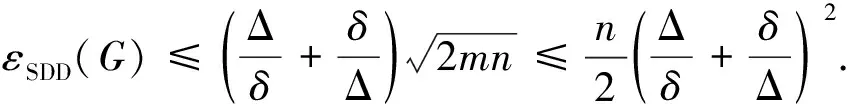
(22)

定理 7设G是一个n个顶点m条边的图，则

ln|detASDD(G)|+n-1-ln 2.

证明对于任意的x>0，有x≥1+lnx. 则

η1+n-1+ln|detASDD(G)|-lnη1.

因为h(x)=n-1+x+ln|detASDD|-lnx在x∈[1，+∞)是单调递增的，由定理1可知

ln|detASDD(G)|+n-1=

ln|detASDD(G)|+n-1-ln 2.