与函数零点相关的参数范围求解问题的策略分析
2022-12-19叶启海范习昱
叶启海 范习昱
(江苏省镇江市丹徒高级中学 212143)
函数零点问题因为涉及到基本初等函数的图象和性质、导数的应用,又渗透着转化化归、数形结合、函数与方程等思想方法,在培养思维的灵活性和创造性等方面起到了非常明显的作用,且对学生的综合素质提出了很高的要求,学生处理起来感到棘手,下文从四个方面加以分类例析.
1函数与方程思想,直接求根策略
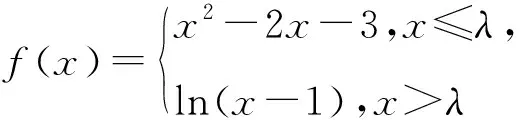
A.[-1,2)∪[3,+∞) B.[1,2)∪[3,+∞)
C.[1,2)∪[2,+∞) D.[1,+∞)
解析令x2-2x-3=0,可得x=-1或x=3.
令ln(x-1)=0,可得x=2.
因为x-1>0,所以x>1.
所以λ>1.
作出图象(如图1),结合图象可得1≤λ<2或λ≥3时,f(x)恰有两零点.故选B.
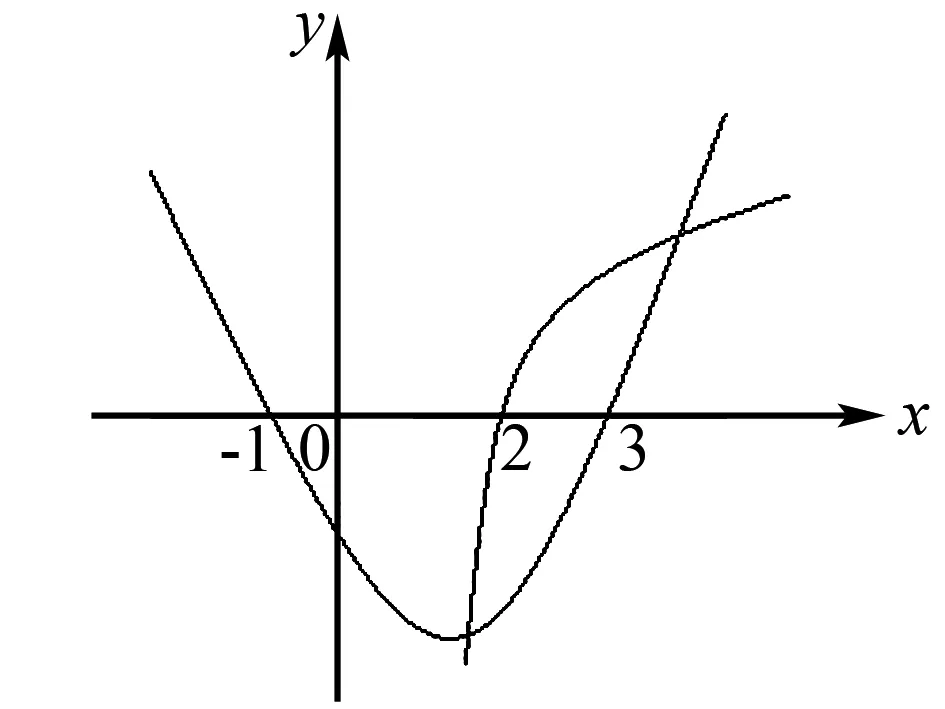
图1
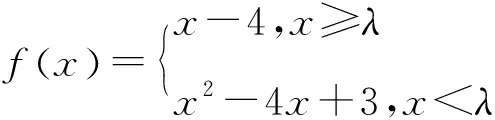
解析(1)不等式的解集为1,4.(过程略)

图2
(2)作出函数y=x-4与y=x2-4x+3的图象,如图2所示,由图可知,当λ≤1时,函数fx有1个零点;
当1<λ≤3时,函数f(x)有2个零点;
当3<λ≤4时,函数fx有3个零点;
当λ>4时,函数fx有2个零点.
所以当函数fx有2个零点时,λ的取值范围为1,3∪4,+∞.
点评根据零点的定义,函数fx零点是方程fx=0的根,因此利用函数与方程思想直接求根策略是处理零点参数问题的首要策略.这两个案例的参数都是分段函数分界出的自变量的取值,我们可以先直接求出每段的零点,然后将参数与这些零点的关系进行讨论,不难得出结果.
2 转化与化归思想,数形结合策略
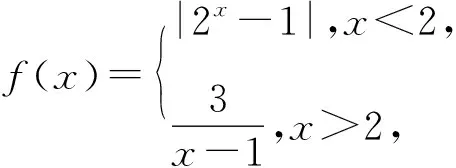
A.(0,1) B.(0,2) C.(0,3) D.(1,3)
解析画出函数f(x)的图象,如图3所示.
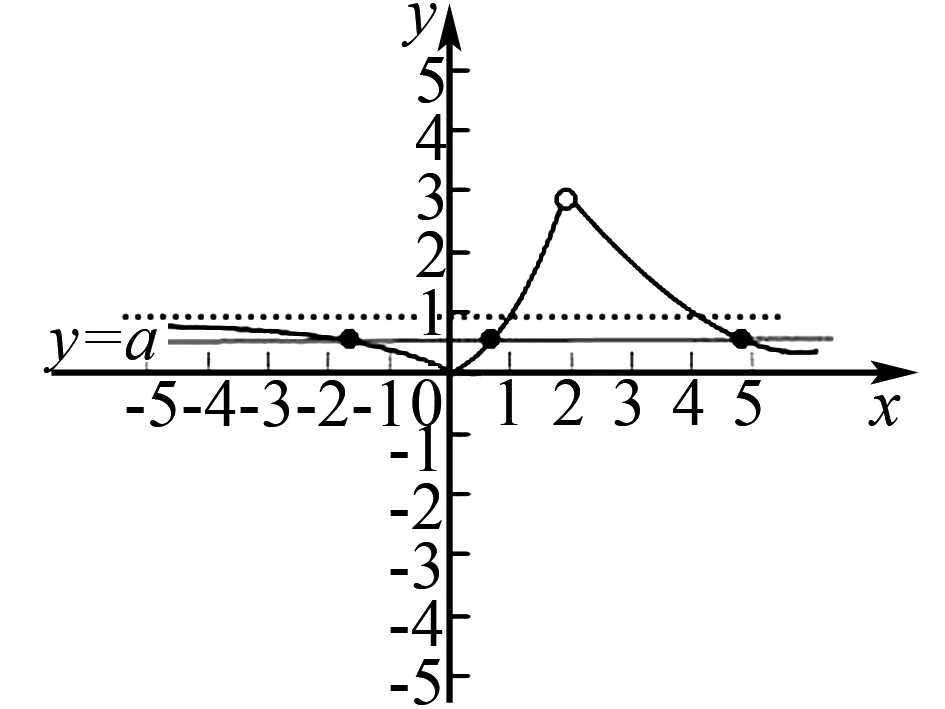
图3
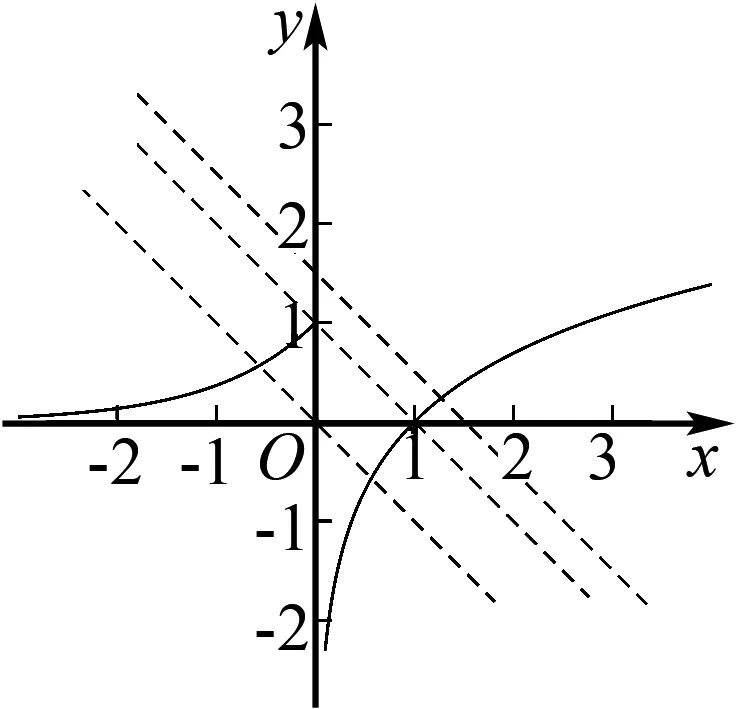
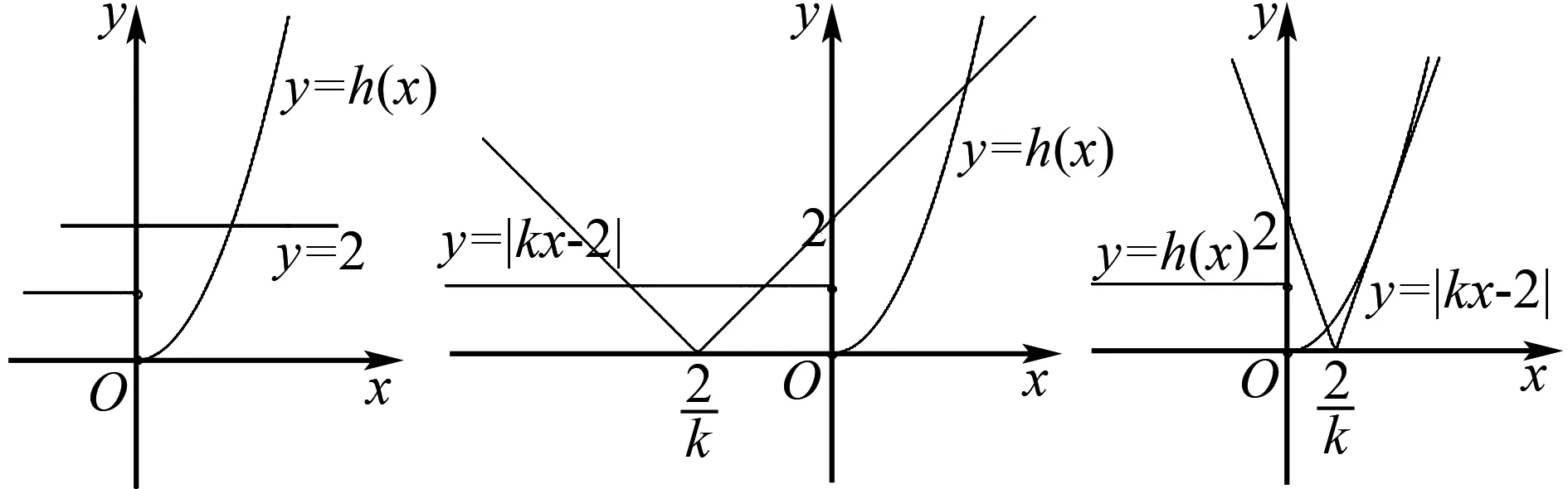
等价于方程f(x)-a=0有三个不同的实数根,即y=f(x)和y=a的图象有3个不同的交点,结合图象,0 A.[-1,0] B.[0,+∞) C.[-1,+∞) D.[1,+∞) 解析函数g(x)=f(x)+x+a存在2个零点,即关于x的方程f(x)=-x-a有2 个不同的实根,函数fx的图象与直线y=-x-a有2个交点,作出直线y=-x-a与函数f(x)的图象,如图4,由图可知,-a≤1,解得a≥-1,故选C. 图4 图5 图6 图7 故选D. 点评函数零点是函数与x轴交点的横坐标,具有很强的几何特征,采取数形结合的策略是处理函数零点问题的最为常见而有效的策略.这一策略基于一种转化与化归的思想,即方程f(x)=0有实数根⟺函数y=f(x)的图象与x轴有交点的横坐标⟺函数y=f(x)有零点,围绕三者之间的关系,是可以探求参数的范围.例3转化为函数图象与一条水平直线的交点问题,例4转化为函数图象与一组平行直线的交点问题,例5转化为函数图象与斜率变化的直线交点问题,这里解题的关键是运用运动的观点,立足参数的几何含义和题目中有关零点的条件,加以分类讨论从而解决参数范围. A.a<-1,b<0 B.a<-1,b>0 C.a>-1,b<0 D.a>-1,b>0 根据题意函数y=f(x)-ax-b恰有3个零点,则函数y=f(x)-ax-b在(-∞,0)上有一个零点,在[0,+∞)上有2个零点,如图8: 图8 所以a>-1,b<0.故选C. 例7(2020年全国卷(文科)(新课标Ⅰ))已知函数f(x)=ex-a(x+2). (1)当a=1时,讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. 解析(1)当a=1时,f(x)的单调递减区间为(-∞,0),单调递增区间为(0,+∞); (2)若f(x)有两个零点,即ex-a(x+2)=0有两个解. 令h′(x)>0,解得x>-1, 令h′(x)<0,解得x<-2或-2 所以函数h(x)在(-∞,-2)和(-2,-1)上单调递减,在(-1,+∞)上单调递增,且当x<-2时,h(x)<0,而x→-2+时,h(x)→+∞,当x→+∞时,h(x)→+∞. 点评根据零点个数判断一个或多个参数的范围问题,其难度较大,但解题基本思路和工具依然没有变化,即利用零点存在定理,结合数形结合、分类讨论思想,加以转化与化归.例6和例7充分利用导数研究函数的性质(单调性和极值、最值等)来确定参数范围,这表明函数零点问题与导数的交汇性很深,也凸显导数功能的强大. (1)求a的值; (2)函数g(x)=f(x)-log2k,若函数g(x)有零点,求参数k的取值范围. 解析(1)a=2(过程略). (2)若函数g(x)有零点,则直线y=log2k与曲线y=f(x)有交点. (1)当m=1时,解不等式f(x)+1>f(x+1); (2)设x∈[3,4],且函数y=f(x)+3存在零点,求实数m的取值范围. 解析(1)不等式f(x)+1>f(x+1)的解集为(-∞,0)∪(1,+∞)(过程略). 即m=-(x+1)2+4在[3,4]上有解. 函数y=-(x+1)2+4在[3,4]上单调递减,则y∈[-21,-12],从而,实数m的取值范围是[-21,-12]. 点评关于零点存在性问题,一般都可以变量分离后,转化为函数的值域问题,例8和例9都是这种做法,当然,面对零点具体个数的分析,函数值域策略有时会失灵. 与函数零点相关的参数范围求解问题是高考的热点,是高考命制压轴题的主要源泉之一,我们需要引起足够重视.处理零点相关的参数问题,我们有如下常用的策略: (1) 直接求根策略:解方程f(x)=0. (2) 数形结合策略:先对解析式变形,在同一平面直角坐标系中画出函数的图象,然后数形结合求解. (3) 导数分析策略:面对零点具体个数的讨论求参范围时用导数分析. (4) 函数值域策略:零点的存在问题一般可以转化成求函数值域问题. 我们相信,只要熟练掌握这四种策略,求解与函数零点相关的参数范围问题并不是一件很难的事.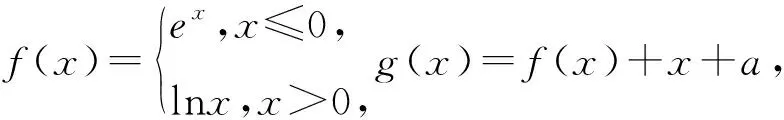

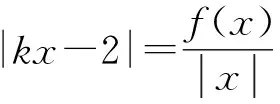
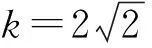
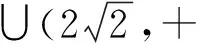
3 转化与化归思想,导数分析策略
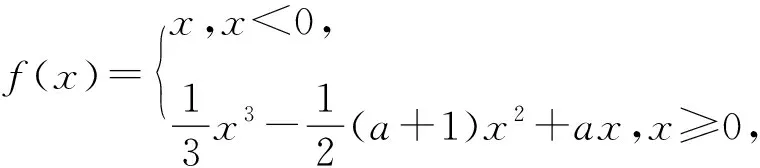
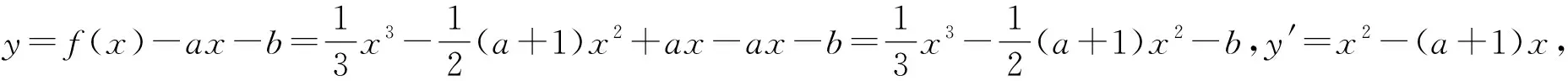
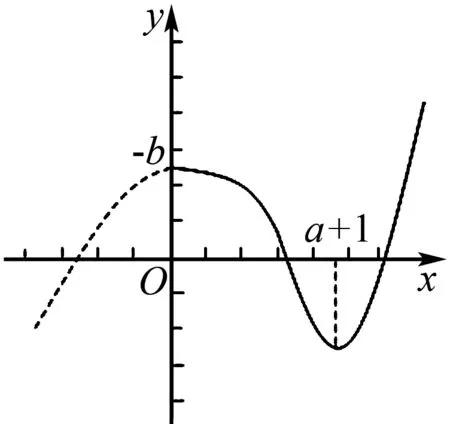
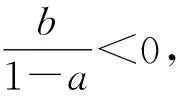
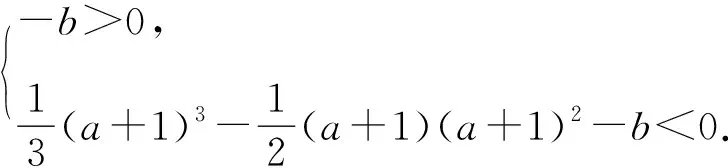

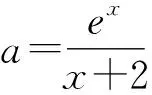
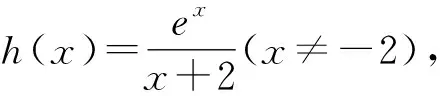
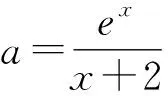
4 变量分类思想,函数值域策略