解决高中物理极值问题常见的几种函数思想

陈庆涛

(甘肃省庆阳一中 745000)

1 一元二次函数求解极值问题

例1如图1所示，一带电微粒以竖直向上的初速度v0从A点射入一水平向右的匀强电场中，微粒的电荷量为q=-2×10-8C、质量为m=1×10-6kg，当微粒运动到B点时速度方向水平向左、大小也是v0，B点比A点高h=20cm，且B、A两点的连线与水平方向间的夹角为45°，g=10m/s2， 求：

(1)匀强电场的场强E的大小；

(2)该微粒初速度v0多大；

(3)该过程中带电微粒的最小速度为多少.

图1

解得：UAB=-100V

由于A、B两点的连线与水平方向的夹角为45°，所以A、B两点沿着电场线方向上的距离为:d=h

(3)带电微粒从A点到B点的过程中，在水平方向上做匀加速直线运动，则：v0=a水平tAB

在竖直方向上做匀减速直线运动，则：v0=gtAB

则：a水平=g

在竖直方向上，设经时间t微粒的速度为vy，则：vy=v0-gt

在水平方向上，设经时间t微粒的速度为vx，则：vx=gt

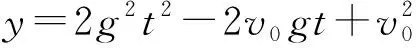
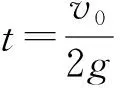
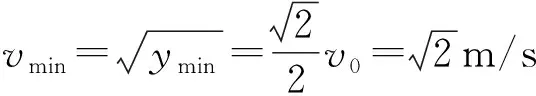
例2如图2所示，内壁光滑的四分之一细圆弧弯管与一可伸缩的竖直光滑细管平滑连接，细管的下端固定在水平地面上，整个装置处在竖直平面内，细圆弧的右管口切线水平.竖直细管底部有一高度可忽略不计的弹射装置，该弹射装置可以让视为质点的小球从细管底部瞬间获得足够大的速度v0，通过调节竖直细管的长度，可以改变小球到达四分之一细圆弧弯管口的速度，从而改变小球做平抛运动的水平位移x，重力加速度为g，则小球做平抛运动的水平距离x的最大值是( ).

图2

答案：B

2 三角函数知识求解极值问题

例3如图3所示，斜面体的倾角为θ，质量为M.若将一质量为m的小物块放在斜面体上时，小物块恰好能沿斜面匀速下滑，这一过程中斜面体保持静止.现用如图3所示的力F拉着小物块，使小物块沿斜面匀速上升，力F与斜面体间的夹角为α，这一过程中斜面体也保持静止.

(1)当α为多大时力F有最小值，力F的最小值多大？

(2)当α=θ时，水平面对斜面体的静摩擦力多大？

图3

解析(1)小物块在斜面上匀速下滑时，有：mgsinθ=μmgcosθ

解得：μ=tanθ

小物块在力F的作用下沿斜面向上匀速运动时，有：

沿斜面方向上：Fcosα=mgsinθ+Ff

垂直于斜面方向上：Fsinα+FN=mgcosθ

又因为：Ff=μFN

解得：

由数学三角函数的知识得：

所以，当α=θ时，F有最小值Fmin，最小值为：Fmin=mgsin2θ

(2)由于斜面体和物块均处于平衡状态，取斜面体和物块组成的整体为研究对象，对

整体进行受力分析，在水平方向上由二力平衡得：

Ff=Fcos(α+θ)

当α=θ时，由(1)问知F=mgsin2θ

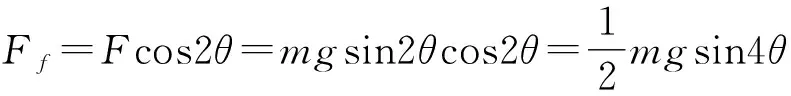
例4如图4所示，倾角为37°的斜面足够长，a点位于斜面b点的正上方2.5m处，现以v0=2m/s的速率抛出一个可视为质点的小球，小球初速度的方向不定，小球运动的轨迹与abO处在同一竖直平面内，取g=10m/s2,sin37°=0.6.则小球落回斜面的最长时间为( ).

图4

A．1.5s B．1s C．0.5s D．2s

答案：B

3 基本不等式知识求解极值问题

例5如图5所示，已知电源的电动势E=6V，电流表A可视为理想电流表，变阻器R可调的范围为0～10Ω，定值电阻R0=4Ω.将开关S闭合，变阻器的阻值调至R=3Ω时，电流表的示数I=0.5A.求:

(1)电源的内阻r；

(2)当变阻器R多大时，电源的输出功率最大？最大值Pmax是多少？

图5

解得：r=5Ω

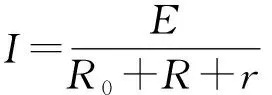
电源的输出功率为:

P=I2(R+R0)

所以，当R=1Ω时，电源的输出功率有最大值Pmax，最大值为：

例6如图6所示，OB是一水平地面，OA是一竖直线，A点距离点O的高度h可调节，O点与B点间的距离为x.先将一可视为质点的小球从A点以合适的速度水平抛出，小球每次都能击中水平面上的B点.空气阻力不计，则( ).

图6

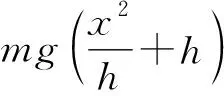
B．h越大，小球到达B点时的动能越大

C．小球到达B点时的动能最小值为mgx

D．h越大，小球到达B点时重力的瞬时功率越大

答案：CD

上述三种方法是高中物理中求极值最重要的方法，也是最常见的方法.高中物理中的极值问题灵活多变，要让学生彻底掌握此种方法，需要平时学生多练相关题目，在此基础上学生才能感悟、积累、归纳极值问题，最终实现灵活运用此方法的目的.