基于深度学习的课堂探究型教学设计*——以“三棱锥的外接球问题”为例

⦿江苏省阜宁教师发展中心 曹子清

1 引言

深度学习是基于数学学科核心内容，以发展高阶思维能力为目标，学生围绕具有挑战性的学习主题进行深度探究，全身心参与学习活动，形成积极的情感、态度，获得发展的有意义的学习过程[1].数学是思维的科学，选择合适的数学模型表达所要解决的数学问题，通过数学学会思维，是培育数学核心素养的有效途径.

深度学习是探究性学习，数学探究能促进学生养成必备品格、练就关键能力、树立正确的价值观.数学课堂教学，既要引导学生掌握数学知识，又要让学生经历数学探究过程，更要让学生体验隐藏在知识背后的数学思想及研究方法.《普通高中数学课程标准(2017年版)》指出：提高从数学角度发现和提出问题的能力、分析和解决问题的能力，通过高中数学课程的学习，树立敢于质疑、善于思考、严谨求实的科学精神[2].在深度思考、充分参与、变式探究中，获得数学学习的创新感和成就感，是数学教学的关键环节.下面，笔者以“三棱锥的外接球问题”设计为例，谈如何做好基于深度学习的课堂探究型教学设计.

2 课堂实录及设计说明

师：三棱锥的外接球问题是一类热点问题，对空间想象、逻辑推理能力的要求比较高.本节课，我们就此类问题进行专题研讨.

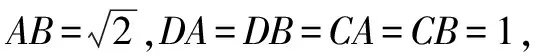
A.π B.2π C.3π D.4π

学生短暂思考后，教师随机选取一小组上台展示.

图1

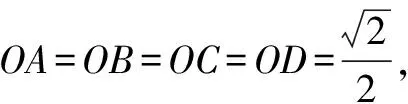
师：解答此问题的关键是什么？

生2：本题图形具有明显的特征，即四面体的两个面是有公共斜边的直角三角形，所以公共斜边的中点到四面体的四个顶点距离相等，即为球心，半径是公共斜边的一半.

师：很好.请归纳一下该数学模型的相关结论.

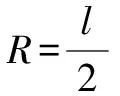
设计意图:深度学习需要从本源性问题入手，增强学生的体验和理解.例1围绕研究几何体外接球的核心元素，从学生熟知的数学模型入手，对具有明显特征的图形进行模型识别，有利于学生的识图能力的提升.

师：若三棱锥有两个侧面是直角三角形，但是不共斜边而共直角边呢？

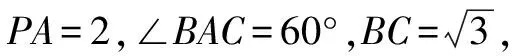
学生活动：

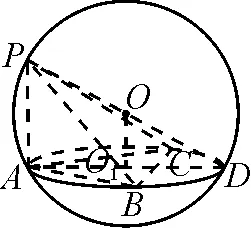
图2

生3：(投影展示图2)设O1为△ABC的外接圆的圆心，连接AO1并延长交外接球于点D，连接PD，过O1作AD的垂线交PD于点O，则O为外接球球心.

师：本题解题关键是什么？

生3：本题的解决，充分利用了球的性质，即球心与小圆的圆心连线垂直于小圆，这也是球的一个显性几何特征.

师：定出球心后，接下来要做什么？

生(齐声)：求半径.

师：请大家解答一下.

学生分小组展开讨论，教师随机选取一小组上台展示.

师：请归纳该数学模型的相关结论.

设计意图:深度学习倡导学生通过探究既要积累学习经验，又要优化思维方式，促进方法的迁移.本板块两个例题的设计，既有相同的要素，即共边的两个面都是直角三角形，又有不同的要素，相近而又相异的模型，建立起深度学习的实践模式，让学生在解决问题中，增强对数学本源的深刻理解.

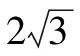
生6：应该把球心放在一个平面图形中.

师：这位同学提供了很好的思路，空间问题应该尽可能地平面化.那么怎么确定这样的一个平面呢？

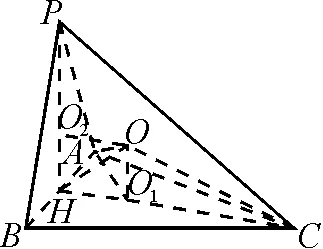
图3

生7：(投影展示图3)因为平面PAB⊥平面ABC，PA=PB，所以取AB的中点H，连PH，CH，设O1为△ABC外接圆的圆心，则三棱锥外接球的球心O在平面PCH内，且OO1⊥CH.

师：为什么？

生8：可证PH⊥平面ABC，OO1⊥平面ABC，所以PH∥OO1,从而球心O一定在平面PCH内.

师：非常好！但是怎样确定球心的实际位置呢？

学生一时安静，不知如何下手.

师：碰到困难时，不妨回到定义解题.球心的性质是什么？

生(齐答)：球心到球面上各个点的距离相等.

师：本题中，应该到三棱锥四个顶点的距离相等.

学生快速解答，教师随机提问一小组上台展示.

师：请归纳一下该数学模型的相关结论.

设计意图:深度学习倡导通过探究具有挑战性的问题，发展学生的高阶思维.本板块通过侧面与底面关系变化，构建形成不同的模型载体，在不同的探究中获得系统的研究方法.抓住球心所在的平面这一关键，利用平面图形构造直角三角形进行求解，使体现学科本质、富有深度思考的学习活动真正发生.

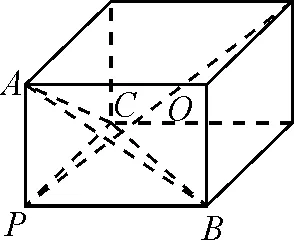
图4

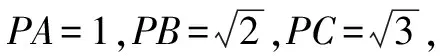
师：大家分小组研究一下.

学生分小组展开讨论，教师随机选取一小组上台展示.

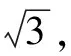
师：很好.能否告诉大家，解答此问题的关键是什么？

生12：图形具有明显的特征，即属于三条侧棱两两垂直的三棱锥的外接球问题，将其补形成长方体，然后找到外接球的球心即可.

师：归纳一下该数学模型的相关结论.

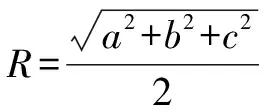
师：刚才我们研究了两类特殊几何体的外接球问题，那么请大家看下面一道题.

A.2π B.4π C.6π D.8π

师：大家先分小组研究一下.

学生小组展开讨论，教师随机选取一小组上台展示.

生14：考虑到四面体ABCD的三组对棱分别相等，可将其补形成长、宽、高分别为x，y，z的长方体，则(2R)2=x2+y2+z2=6(R为球的半径)，得2R2=3，所以球的表面积为S=4πR2=6π.

师：很好.能否告诉大家，解答此问题的关键是什么？

生15：图形具有明显的特征，即属于三组对棱分别相等的四面体的外接球问题，将其补形成长方体，然后找到外接球的球心即可.

师：归纳一下该数学模型的相关结论.

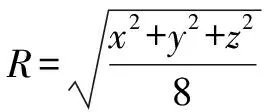
设计意图:数学是充满联系的，不要教孤立的片段，应该教联系的材料[3].深度学习通过用理解性、阶梯式、探究性的问题引导学生深度思考，获得思维的拓展.本板块通过对三棱锥边长关系的变化，设计形成新的图形特征，构建新的数学模型，在问题解决中实现思维创新.

师(总结)：本节课研究了不同类型的三棱锥外接球问题，其关键是寻找球心和半径.大家总结一下有哪些途径？

生17：一是直接利用定义找球心，求半径；二是将三棱锥放入特殊的几何体中，求半径；三是找圆心，找球心，利用直角三角形求半径.

师：在求解的过程中要充分利用平面几何知识寻找几何体中元素间的关系，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.

师：数学中有很多的模型，虽然看似并不相同，但其实有很多的关联，我们要学会研究总结，归类思考.

3 教学启示

3.1 探究型设计需要选择适切的模型载体

深度学习是一种由浅入深、由表及里、从已知到创新的深入探究的过程.利用基本模型，让学生充分经历直观感受、批判优化、意义联接等学习活动，通过观察和想象，积累活动经验，用联系的视野在不同维度的问题探究之间自如切换，形成积极情感体验和高阶思维能力.本节课的探究型教学设计，始终围绕“模型分析—本质确认—意义获得”等环节层层展开，深探究、长智慧、促思维、提学力，助推学生对三棱锥外接球问题的本质思考.因为有适切的模型载体，学生的思维策略逐步明朗且不断深化.

3.2 探究型设计需要持续可视的思维进阶

深度学习在问题情境中对知识进行批判理解、主动联系、整合信息、迁移应用，通过有意义的系列探究问题设计，助推学生由“学科思维”走向“学会思维”，由“认同性思维”走向“批判性思维”，形成系统思维的结构观念，实现思维的可视化.本节课的探究型教学设计，思考的维度和深度不断提升，研究的途径不断丰富，因而创造思维能力、逻辑思维能力和审辨思维能力也随之不断提升.

3.3 探究型设计需要素养培育的有效增值

数学核心素养的提升是综合、持续发展的过程，它需要重视单元整体知识的构建，增强知识系统化和结构化的网路结构意识.本节课的探究型教学设计，既有教师关键节点处的“导”，更有学生疑难处的“探”，更有结课时的思维导图，新颖而不断深入的问题情境，帮助学生确立研究问题的思维路径，不断地发现问题、生成问题，然后完善问题、发展问题，增强了学生学好数学的自信心和成就感.

探究型设计有助于深度教学、深度学习的开展，而强化教学设计的研究和课堂探究活动的深入展开，还需要更多的作为和实践.