数学与生活——以“用表格表示变量间的关系”为例

王亭雅

（广东省佛山市南海区里水双语实验学校，广东 佛山 528244）

大部分课堂教授新知都是侧重于传授，忽略了生活的真实情景，未将生活与数学知识相结合，导致学生很难接受新知，课堂效率较低。如果将生活与数学知识结合起来，让学生体会数学的意义，才能激发学生的主观能动性，使课堂效益最大化[1]。除此之外，社会的发展需要更多的人才综合能力，这也在一定程度上说明了理论与实践相结合的重要性，要将知识应用于生活中，关键在于教师如何正确引导学生将新知与生活融会贯通[2]。所以，将初中数学与生活情境相结合具有重大意义。

1 初中数学与生活联系的意义

1.1 激发学习兴趣

初中学生处于青春期阶段，部分学生存在逆反心理，他们在学习的过程中，如果面临困难，很可能对这一学科失去兴趣，导致课堂难以正常进行。因此，教师应转换教学方式，激发学生的热情。最直接的方式就是创设生活情境，将学生置身于真实的生活情景中，启发学生用数学的眼光看待生活。情景教学最大的优势就是能将抽象知识具象化，尤其是一些抽象的概念问题，大部分学生很难深入理解，如果不及时调整教学方式，则会影响后续的学习[3]。所以，创设生活情境，以生活为导向来吸引学生，将复杂问题简单化，是提高课堂效率的有效途径。

1.2 符合新时代需求

社会所需求的，不是仅仅只会用数学知识来解题的“学霸”，而是能真正将数学知识应用于生活中解决实际问题的人才。在教学过程中，教师应着重培养学生解决实际问题的能力，将数学知识与生活相结合，刺激学生积极参与探索新知的过程，通过实践活动提高独立探索、合作交流的能力，最大程度上挖掘学生的潜能，培养用数学知识解决实际问题的能力，从而满足社会对人才的需求。

2 课堂实例

数学教学的最终目标就是引导学生利用数学知识解决生活实际问题，教师应从学生的角度出发，结合学生的生活体验，将生活案例融入课堂教学，通过创设问题情境，提高课堂效率。本文将以“用表格表示变量间的关系”为例，阐述如何将数学教学与生活相结合。

2.1 课堂引入

观看植物在一年四季中的生长状态，感受事物的变化。

教师：（1）我们生活在这千变万化的世界中，大家能举出生活中存在变化的例子吗？（2）在这个变化过程中，有哪些量发生了变化？哪些量始终不发生变化？

设计意图：问题（1）是启发学生观察生活，将生活与数学联系在一起，学生通过自己寻找发生变化的例子，是直接经验的体现，有利于后续内容的展开。问题（2）是进一步引导学生区分变与不变的量，为新概念的引入做好铺垫。

课堂反馈：大部分学生都能找出生活中存在变化的例子，例如钟表时间的变化、温度的变化等等，但是对于同一个场景中，很难发现始终不发生改变的量。教师可以适当提醒学生，根据学生的生活，以每日水果作为例子引入。苹果的重量越多，总价格会随之升高，苹果的单价是不变的，借此实例引出自变量、因变量以及常量的概念。

2.2 活动1：情境运用

以小组为单位，学生互相举例并说出自变量、因变量以及常量。

设计意图：学习新概念之后，及时联系生活的实例，在具体情境中明确自变量、因变量以及常量，有利于新知的内化。学生之间沟通交流，培养语言表达能力。

课堂反馈：学生积极性较高，思维活跃，通过数学与生活的联系，感受到数学的快乐与意义。

2.3 活动2：小车滑行

教师：城市中修了很多高架桥，高架桥的坡度对汽车的安全行驶有重要意义。有一个学习小组对此产生了兴趣，于是做了一个实验:小车滑行。这个小组利用同一块木板，测量小车从不同的高度下滑的时间。

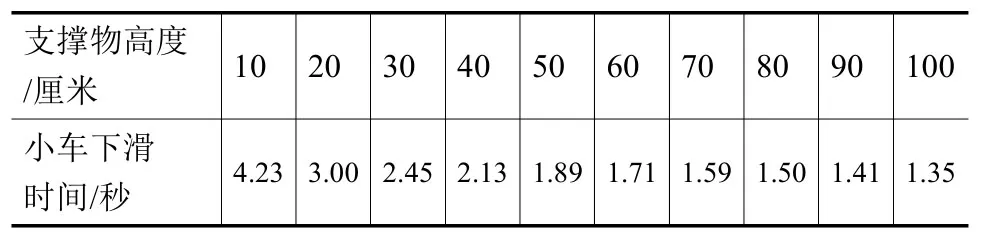
支撑物高度/厘米 10 20 30 40 50 60 70 80 90 100小车下滑时间/秒 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35

（1）当支撑物高度为70厘米时,小车下滑的时间为______。

（2）上表反映的是__________和____________之间的关系；自变量是__________，因变量是__________，常量是_________。

（3）如果用h表示支撑物高度，t表示小车下滑时间,随着h逐渐变大，t的变化趋势是什么?

（4）h每增加10厘米，t的变化情况相同吗？

（5）估计当h=110厘米时，t的值会是1.48吗？会是1.26吗？

设计意图：用生活中的高架桥引入，让学生理解做此实验的必要性，实验结果用表格呈现出来，让学生学会读表格，问题的设置由易到难，循序渐进。问题（1）是让学生通过表格提取有效信息，体会因变量与自变量是一一对应的。问题（2）是巩固新知，检测学习成果，使学生区分自变量与因变量以及常量。问题（3）渗透了用字母表示变量的思想，并让学生观察表格，发现因变量的变化趋势。问题（4）（5）由小组合作完成，体会表格的预测功能。

教师：支撑物的高度能无限变高吗？

课堂反馈：学生意识到木板的长度有限，支撑物的高度最多等于木板的长度。少部分学生思维缜密，能发现支撑物的高度不能等于木板的长度，从而体会到自变量是在一定范围内变化的量，数学不能脱离生活实际。

情境重现：如果小组利用不同长度的木板，测量小车从相同高度下滑的时间，那么在此变化过程中，常量，自变量，因变量分别是？

设计意图：考查学生是否理解概念，让学生体会常量和变量并不是绝对的，常量和变量是对于某一个变化过程而言的。同一个量在不同的问题情境中，可能是常量，也可能是变量。

3 教学反思

3.1 以学生为主体

教师要以学生的直接经验为主，将学生的生活经验融入课堂，合理创设生活情境。帮助学生将形象思维建构起来，使其逐步深化理解，最终形成抽象思维。在上述案例中，以学生的课间水果餐为例，让学生直观感受到水果的价格随着水果重量的变化而变化，从而使学生初步体会因变量与自变量的关系。这样的课堂引入做到了以学生的直接经验为主，成功吸引了学生的注意力，拉近学生与新知的距离，有利于后续教学的开展。

3.2 联系生活情境

数学不能只停留于知识表面，而要注重联系生活，所以需要教师在教学过程中适当联系生活情境，让学生意识到数学来源于生活。通过与现实生活相结合，数学知识的系统性、实用性才能显现出来。同时，现实生活的素材还能激发学生的学习兴趣，让传统枯燥的课堂变得有趣，从而提高课堂效率[4]。在上述教学过程中，小车滑行试验是书本上的例子，但是教师通过生活中的高架桥巧妙引入，让学生明白小车滑行试验来源于生活，数学和生活紧密相关，每一个数学例子都能与生活中的场景一一对应，他们是不可分割的。

3.3 激发学生兴趣

适当的讨论交流是有必要的，教师应根据学生的性格特征适度调整课堂活动。面对这些学生，教师应给予其更多的表现机会，这样不仅可以培养学生合作、沟通交流的能力，在讨论过程中不断加深对新知的理解，还能使学生树立信心，进而形成良性循环机制[5]。比如，学生以学习小组为单位，互相找一找生活中存在变化的例子，并明确因变量与自变量。这一过程虽然看似简单，却是极其有效的，因为每个学生都是独立的个体，想法与视角呈现多样化，在讨论过程中给予了学生充足的想象空间，从而使他们对新知的理解更透彻。