应用型本科院校学生在极限学习中的障碍及对策研究

张倩倩

（湖北大学知行学院，湖北 武汉 430014）

0 引言

高等数学又被称为“微积分”，字面含义“用微的办法分析”和“用积的方法处理”，整本书的内容主要围绕微分和积分两大类。无论关于微分还是积分的相关概念都借助了极限来定义，极限可以称作是微积分的“灵魂”，只有理解极限这一抽象概念，才能更好地学好微积分并加以运用。由于科学水平的限制，在解决实际生活中的相关问题时我们并不能求出精确解，而我们也只需要通过观察无线变化过程得到一个近似解，极限的概念就是在这种情况下应运而生，在《庄子·天下篇》中就有“一尺之棰，日取其半，万世不竭”的记录。在本校的实验教学过程中，发现学生在学习极限的过程中存在两个困难，一是对于极限的“-N”定义存在语言表征障碍，二是求解极限障碍。

1 语言表征障碍及对策

1.1 语言表征障碍

极限按照研究对象可以分为数列极限和函数极限。根据函数的定义，数列可以看成自变量为正整数n的函数，也即是说数列是一种特殊的函数，区别在于自变量所属定义域不同。由于本校非数学专业学生采用的教材中，极限知识点处于第一章，且学生已在高中接触过数列。极限在课堂讲解过程中通常采用数学语言描述相关定义和定理，关于数列极限一般写成如下：

（1）不理解数学符号代表的含义。

（2）不清楚数学符号之间的关系。

（3）不明白定义的作用。

函数极限由极限条件自变量的趋向不同，又可分为自变量趋向于无穷大和自变量趋向于固定值，有定义和定义。

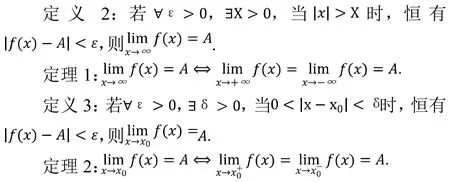
数列极限与函数极限定义中出现的语言障碍类似，接下来以数列极限为主要研究对象。

1.2 语言表征障碍对策

根据学生出现的问题，解决措施有：

（1）详细解释这个定义中所有的模糊点。

（2）采用数形结合。

给出常见的几组数列，让同学们在数轴上按照顺序描点观察。或把数列通项公式看成函数，借助导数画出函数的大致图像（只看自变量为正整数的部分），观察其趋势。需要注意的是，数列极限是点，而函数极限是连接的曲线。

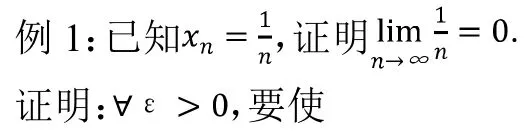
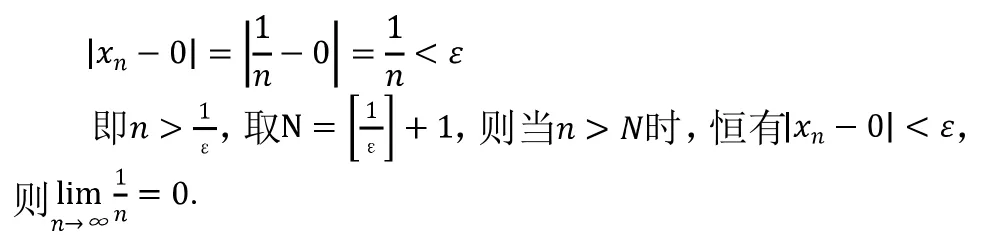
2 求解极限障碍

课本上介绍求解极限的方法有很多，两个重要极限、等价无穷小替换、无穷小的性质、无穷小与无穷大的关系、洛必达法则这些方法适用于所有的类型，连续的定义、导数的定义和泰勒展开式可以求自变量趋向于固定值的极限。

虽然方法很多，但大多数学生遇到求极限的题目仍然没有思绪，没有固定的做题思路，对于方法要求的条件不清楚导致出错。下面主要分为两个方面论述：一是做题思路，二是做题易错点。

2.1 整理做题思路

看到一道极限题目，应先观察极限条件，根据极限条件判定计算方法。若自变量趋向于有限值0，做题步骤如下：

（2）判定函数表达式能否化简整理？在做题的过程中通常用到的有四种方法：根式有理化、分式相加减通分、因式分解消公因子、分子凑出来分母。化简之后再次回到第一步。若不能化简，进行第三步。

（3）利用无穷小和无穷大的关系，若函数倒数的极限为无穷小，则函数为无穷大（极限不存在）。若函数倒数的极限不存在，则优先考虑两个重要极限、无穷小的性质、等价无穷小、导数的定义、泰勒展开式、洛必达法则。

若自变量趋向于无穷大，做题步骤如下：

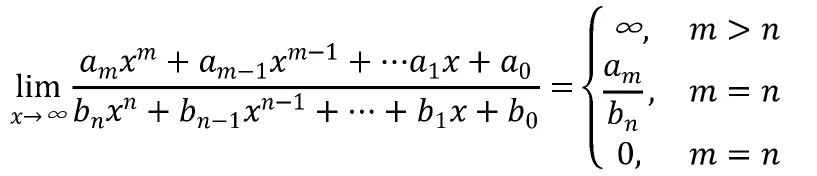
以上结论对数列极限也适用。

（2）当结论不能使用时，则考虑通用方法如：两个重要极限、无穷小的性质、等价无穷小、洛必达法则。

2.2 做题易错点

无论是求解数列极限还是函数极限，最终结果只有两种，一种是极限存在可求出具体数值，一种是极限不存在。在平时的课堂练习中，发现学生混淆极限不存在的情况。极限不存在有以下三种情况；（1）无穷大。（2）极限不确定，如正弦函数在时。（3）左右极限不相等，如反正切函数在时。

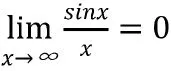
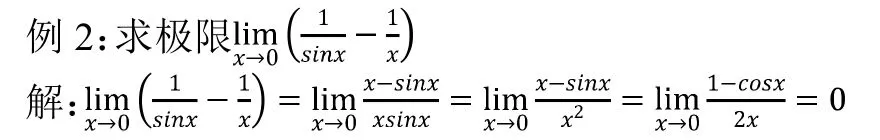
这道题目很容易做错，易错点如下：第一个等号处直接使用等价无穷小代换第二个等号处分子使用等价无穷小。正确做法：先通分，分母等价无穷小，洛必达法则，接下来无论使用洛必达法则还是等价无穷小都可以得到正确答案“0”。

在应用型本科学生的教学过程中发现，学生对于知识点的掌握不是很透彻，没有意识到课本上所给的定义、定理和性质才是我们做题的依据。题目一直在变化，但万变不离其宗，就像盖房子一样，只有把地基打好，上面的建筑才不会倒。面对学生在学习大学数学中出现的各种障碍，讲懂基础定义、定理和性质才是最好的应对对策。