不同形状微肋阵换热特性数值分析

李慧君， 李 东， 张久意， 陈启涵， 王庆五

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

0 引 言

随着科学技术的发展，微机电系统(MEMS)越来越多地被运用在生活中[1]。所谓微机电系统，是指尺寸在几mm甚至更小的独立智能系统。有文献[2]指出电子元件在70～80℃的环境下工作，温度每提高1℃，其可靠性就会下降约5%。故在狭小空间内的散热问题在过去十几年中成为了研究热点之一[3-7]。

微通道热沉是一种高效紧凑式热沉[8]，通常当量直径在10～1 000μm之间，换热能力可达500W/cm2[9]，因其具有体积小、可靠性高、传热能力强等优势[10]，已被广泛应用于解决微机电系统的散热问题。作为现阶段电子芯片的主要散热工具，研究微通道热沉的换热特性已成为本学科的主流问题之一。

国内外已有许多学者对微通道热沉进行了研究。张秀强等[11]通过数值模拟对比不同截面形状的微针肋在不同Re数时的换热特性，发现传热系数随着Re数的增大而增大；相同Re数时，圆形肋片的换热效果最好，壁温最低，方形肋片的换热效果最差，壁温最高。杜保周等[12]搭建不同截面形状微肋阵的实验平台，发现椭圆形肋片换热效果最差，圆形肋片换热效果最好。杨宇辰等[13]通过数值模拟对比了不同孔隙率的叉排圆形微针肋热沉的流动和传热特性，发现孔隙率较大的微肋阵随着热流密度的增大，换热效果明显增强。Avramenko等[14]对不同孔隙率的微通道进行了数值模拟，发现随着孔隙率的减小，会导致壁面附近温度的减小，换热能力增强。Wen等[15]搭建不同间距与水力直径的锯齿形肋片实验平台，发现肋片间距与水力直径越小，传热系数越大。Tullius等[16]对不同形状肋片和间距在工质为单相时的换热及流动特性进行了数值模拟，发现三角形肋片换热性能最好，椭圆形肋片最差，肋片间距的减小使换热增加，并得到了关于肋间距的传热系数预测关联式。Shah[17]分析13种不同流体在不同尺度下的数据，发现表面张力的影响在微尺度条件下更重要，并得到了相关的传热系数预测关联式。Shah[18]提出了一种新的传热系数预测关联式对不同尺度下传热系数的预测具有较好的一致性。还有许多学者对微通道热沉的传热系数进行了预测[19-23]。

综上可知，现阶段关于肋间距对不同形状肋片的沸腾换热影响的研究较为有限。因此，本文改变质量流速、热流密度与肋片间距，研究各因素对不同形状肋片换热特性的影响，并由此提出新的沸腾传热系数预测关联式。

1 模型建立

1.1 几何模型

为研究肋片对换热特性的影响，本文建立了长、宽、高分别为56mm、5.8mm和0.5mm的微通道热沉。为提高换热能力，采用错列排列方式，并选用圆形、菱形和水滴形3种不同形状的肋片，如图1所示。几何参数如表1所示。

图1 微肋阵热沉示意图Fig. 1 Schematic diagram of mini fin array heat sink

表1 肋片几何参数Tab.1 Basic parameters of mini fin (mm)

为减少计算量，选取0.75mm、1.2mm和2mm三种不同的纵向间距。为简略表示不同形状的肋片，用yx、lx和sd分别代表圆形、菱形和水滴形肋片。

1.2 数值模拟

对工质进行如下假设：换热工质为受重力影响，且具有表面张力，则对流传热微分方程为[24]

(1)

(2)

(3)

考虑到干度与质量流速和热流密度等因素有关，则微通道热沉出口干度的计算式为[12]

(4)

微通道热沉内部面积为[12]

A=ηfnPH+2HL+WL-nAcfin

(5)

微通道热沉沸腾传热系数为[12]

(6)

数值模拟采用VOF模型与Coulped算法，动量方程、能量方程与湍流方程均采用二阶迎风格式。

1.3 模型验证

1.3.1 网格无关性验证

分别选取125万、228万和301万的网格，进行数值模拟的对比，最终得到的结果最大误差为3.51%，由此证明网格无关性。因此本文选取228万的网格进行数值模拟，模拟结果如表2所示。

表2 不同网格数模拟结果对比

1.3.2 数学模型验证

利用文献[25]中的几何、计算条件及实验结果与数值模拟结果进行比较，最大误差为5.4%，符合实际需求，由此证明数学模型的准确性。对比结果如图2所示。

图2 实验值与模拟值比较Fig. 2 Comparison of experimental value and simulated value

2 结果分析

2.1 干度对沸腾传热系数的影响

在相同质量流速时，干度越大，沸腾传热系数越小，如图3所示。这是由于干度越大，汽体占比越大，而汽体换热能力较差，使整体的沸腾传热系数较小。

图3 干度对沸腾传热系数的影响Fig. 3 Influence of dryness on boiling heat transfer coefficient

在质量流速为42.7g/(cm2·s)时，随着干度的增加，圆形肋片的沸腾传热系数最大，菱形肋片的沸腾传热系数最小，如图3所示。这是由于圆形肋片尾流区存在涡旋，使热阻较大的汽体传热能力增强。菱形和水滴形肋片流固耦合较好，对汽体扰动较小，使沸腾传热系数较小。而水滴形肋片前端是对工质扰动更大的半圆结构，故其沸腾传热系数相较于菱形肋片更大。

2.2 热流密度对沸腾传热系数的影响

相同质量流速时，随着热流密度的增大，单位质量工质吸收热量增加，使沸腾更加剧烈。随着壁面单位面积上汽泡数量不断增加，热阻增大，沸腾传热系数减小，如图4所示。这与文献[12]中的规律一致。

图4 不同热流密度对沸腾传热系数的影响Fig. 4 Effect of different heat flux on boiling heat transfer coefficient

当质量流速为42.7kg/(cm2·s)时，随着热流密度的增大，肋间距为0.75mm的圆形肋片沸腾传热系数最大，肋间距为2mm的菱形肋片沸腾传热系数最小，如图4所示。这是由于热流密度为60 W/cm2时，微通道内液相占比较大。当工质沸腾时，小汽泡的出现对工质的换热能力起增强作用。当热流密度增大到140 W/cm2时，汽泡的生长速度加快，汽泡逐渐转变为气膜，此时影响换热的主要因素变为气膜厚度。菱形和水滴形肋片由于流固耦合更好，气膜较易包裹在肋片外部，而圆形肋片由于尾迹流的存在，破坏了附在肋片表面的气膜，使其换热能力比菱形与水滴形肋片分别提升约113%和43%。不同热流密度下肋间距对沸腾传热系数的影响不同。在热流密度为60 W/cm2时，肋间距的增加使沸腾传热系数减小约17%。当热流密度增大到140 W/cm2时，肋间距的增加使沸腾传热系数减小约8%。

2.3 质量流速对沸腾传热系数的影响

相同热流密度时，随着质量流速的增加，使工质各部分间发生剧烈的混合，同时单位质量工质吸收热量减小，干度减小，热阻减小，进一步增强换热，如图5所示。这与文献[26]结论相同。

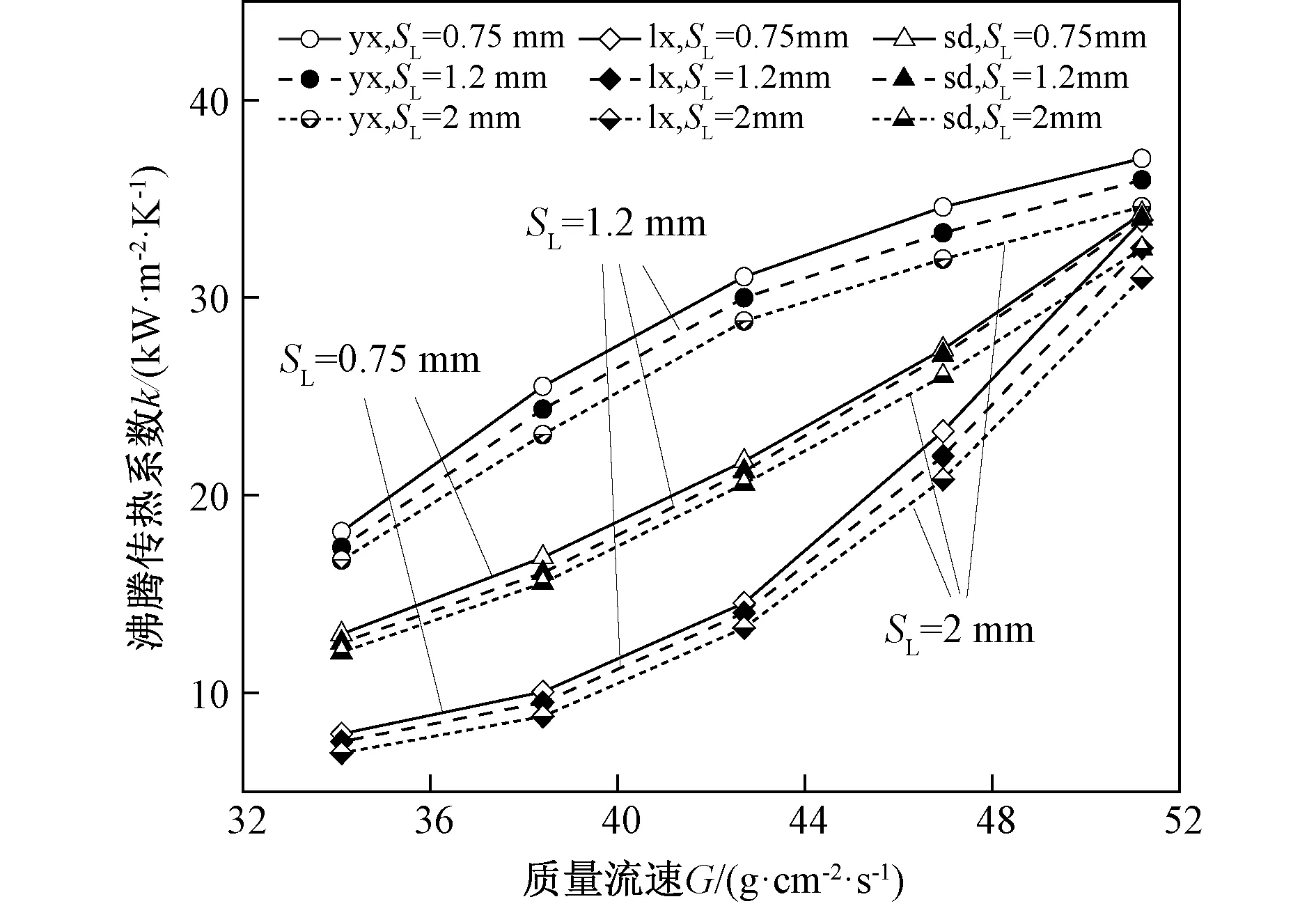
图5 不同质量流速对沸腾传热系数的影响Fig. 5 Effect of different mass velocity on boiling heat transfer coefficient

当热流密度为95 W/cm2时，随着质量流速的增加，肋间距为0.75mm的圆形肋片沸腾传热系数最大，肋间距为2mm的菱形肋片沸腾传热系数最小，如图5所示。这是由于质量流速为34.1g/(cm2·s)时，单位质量工质吸热量较大，使微通道内汽相占比较大，热阻较大。圆形肋片由于二次流的存在，使沸腾传热系数比菱形和水滴形肋片分别提高约59%和30%。当质量流速增大到51.2g/(cm2·s)时，单位工质吸热量减小，使干度减小，热阻减小。圆形肋片尾部二次流对换热能力的影响减小，其沸腾传热系数比菱形和水滴形肋片分别提高约9%和8%。当肋间距从0.75mm增加到2mm时，肋片对工质扰动减小，使沸腾传热系数减小约8%。

2.4 对微肋阵的综合评价

为研究各因素对微通道热沉综合性能的影响，使用多目标决策法评估9种不同间距和形状肋片在相同工况下的综合性能。综合性能指标包括出口干度、压降和沸腾传热系数。根据文献[27]中提出的将模糊隶属度融入信息熵的方法来处理各参数的比重，并以此进行评价，因此将综合评价指标设为[27]

(7)

模糊隶属度是将各因素数值进行归一化的参数，可分为增益指标隶属度和减益指标隶属度。所谓增益指标隶属度是指参数值越大越好的参数，而减益指标隶属度反之。则增益指标隶属度为[27]

(8)

减益指标隶属度为[27]

(9)

目标参数的相对权重wi为[27]

(10)

将质量流速为42.7g/(cm2·s)，热流密度为60 W/cm2时数据代入式(7)中，可得到综合评价指标C的数值，其值越大则可视为该种肋片具有更好的综合性能。肋间距为1.2mm的圆形肋片综合性能最好，如图6所示。这是由于圆形肋片的沸腾传热系数较大。随着肋间距的增大，沸腾传热系数有所增加，但增加不大。而肋间距的增大使压降增幅较大[28]，故肋间距为1.2mm的圆形肋片综合性能最好。

图6 各间距及形状肋片的综合评价指标值Fig. 6 Comprehensive evaluation index values of each spacing and shape fin

其中，方案1、方案2和方案3分别代表肋间距为0.75mm、1.2mm和2mm的圆形肋片；方案4、方案5和方案6分别代表肋间距为0.75mm、1.2mm和2mm的菱形肋片；方案7、方案8和方案9分别代表肋间距为0.75mm、1.2mm和2mm的水滴形肋片。

通过上述计算分析，可以看到微肋阵换热器传热系数主要受质量流速、热流密度、肋片形状与肋片间距的影响。为了将这些因素考虑在内，并便于工程应用，本文提出了传热系数预测关联式，以便在工程实际中使用。

2.5 传热系数预测关联式

现阶段已有许多学者针对微通道热沉在不同工况下的换热情况进行了一系列的实验与模拟研究，根据工况变化得到实验结果，并由此分析得到新的沸腾传热系数预测关联式，如Qu&Mudawar关联式[29]。而每个沸腾传热系数预测关联式都有其自身的实验条件，在超出其实验范围的条件下，预测值可能会有所偏差，且有关于肋间距的沸腾沸腾传热系数预测关联式较少，故对此进行研究。

由文献[24]可知，沸腾传热系数与温差、重力加速度、工质密度、汽化潜热、表面张力、工质定压比热容、工质导热系数、工质粘度、加热表面与工质经验常数等因素有关，再引入无量纲参数对其改写，则沸腾传热系数为

k=f(Re,Pr,Bo,We,X,SL,λ,D)

(11)

将式(11)根据增强模型[30]，可改写为

(12)

将质量流速为34.1～51.2g/(cm2·s)，热流密度为30～160W/cm2时计算出的数据代入式(12)进行数值计算，可得到沸腾传热系数预测关联式为

(13)

不同工况时关联式对各形状肋片沸腾传热系数预测有所偏差，因此引入修正系数。由于质量流速对不同形状肋片的换热能力影响不同，则修正系数为

(14)

各形状肋片在SL=1.2mm时沸腾传热系数实验值与预测值的对比，如图7所示。

图7 不同形状肋片沸腾传热系数实验值与预测值比较Fig. 7 Comparison of experimental and predicted values of boiling heat transfer coefficient of different shape fins

使用平均绝对误差来衡量预测关联式的精度，其表达式为[16]

(15)

将不同尺寸和不同纵向间距微肋阵热沉的数据代入式(15)得到的预测误差，如表3所示。沸腾传热系数预测关联式的最大误差为9.71%，基本符合工程实际要求。各形状肋片沸腾传热系数实验值与预测值之比如图8所示。

表3 各形状肋片的MAE值Tab.3 MAE values of mini fins with different shapes

图8 不同形状肋片沸腾传热系数实验值与预测值之比Fig. 8 Ratio of experimental and predicted values of boiling heat transfer coefficient of different shape fins

3 结 论

对圆形、菱形和水滴形肋片的换热特性进行了研究，并拟合得到沸腾传热系数预测关联式。分析结果得到以下结论：

(1)干度随热流密度的增大而增大，随质量流速的增大而减小。

(2)在相同工况下，圆形肋片的沸腾传热系数最大，菱形肋片的沸腾传热系数最小；肋片间距越小，换热性能越好。

(3)不同因素对不同形状肋片的沸腾传热系数的影响程度不同。

(4)肋间距为1.2mm的圆形肋片综合性能最好。

(5)由模拟数据拟合出一种新的沸腾传热系数预测关联式，其平均绝对误差的最大值为9.71%，可较好地预测不同肋片形状与肋间距对沸腾换热的影响。

符号说明

Acfin——单个肋片所占面积，m2；

Aw——加热面面积，m2；

a——待定系数；

Bo——沸腾数；

b——待定系数；

c——待定系数

cp——比定压热容，J/(kg·K)；

D——肋片当量直径，m；

d——待定系数

eij——目标参数i的模糊隶属度

F——待定系数；

f——各个方向上的外力，N；

fb——微团所受体积力，N；

fimax，fimin——第i个目标参数的最大值和最小值；

G——质量流速，g/(cm2·s)

H——微通道热沉的高度，m；

hsp——对于单相工质在管内强制对流换热的实验关联式，其计算式为hsp=0.023Re0.8Pr0.4λ/D，W/(m2·K)；

IEi——第i个目标参数的信息熵；

i——第i个目标参数；

j——第j种肋片当前目标参数的值；

kpre，kexp——沸腾传热系数的预测值和实验值，W/(m2·K)；

L——微通道热沉长度，m；

M——肋片种类的总数

m——工质质量流量，kg/s；

NDij——第j种肋片的第i个目标参数的归一化数值；

n——肋片个数；

P——肋片周长，m；

Q——工质增加的热量，J；

q——加热热流密度，W/m2；

r——汽化潜热，kJ/kg；

SL——沿热沉方向间距，m；

Sr——沿热沉宽度方向间距，m；

T——工质温度，K；

u——工质的热力学能，J；

W——微通道热沉宽度，m；

We——韦伯数；

X——Martinelli系数；

z——目标参数的个数；

ηf——肋片的肋效率；

λ——工质的导热系数，W/(m·K)；

μ——工质的动力粘度，Pa·s；

ρ——工质密度，kg/m3；

τij——微团所受剪切力，N。

下角标

exp——实验值

in——入口

pre——预测值

s——饱和状态

w——壁面