基于矩阵算法和BP神经网络的智能站二次系统故障定位方法

2022-12-17戴志辉耿宏贤韩健硕李金铄

华北电力大学学报(自然科学版) 2022年6期

戴志辉，耿宏贤，韩健硕，李金铄，方伟

(1.华北电力大学电气与电子工程学院，河北保定 071003；2.国网河北省电力有限公司沧州供电分公司，河北沧州 061000)

0 引言

智能变电站是智能电网的重要组成部分，准确可靠的二次系统故障分析及定位对提升智能站运行水平、保障电力系统安全稳定运行至关重要。随着智能电网建设的不断发展、变电站自动化设备的广泛应用，变电站设备数量和信息网络规模大大增加。信息物理系统(cyber physical system，CPS)依托丰富的传感监测设备以及完善可靠的通信网络，是集成了通信、控制等信息过程和稳定、可靠物理过程的综合化系统[1]。智能变电站已成为典型的信息物理系统，建立准确、合理的变电站二次系统信息物理融合模型用以描述信息系统与电力物理系统的耦合与交互的过程，更有利于分析其故障过程，为故障定位奠定完善的模型基础。文献[2]采用图论对电力系统进行建模，文献[3]利用关联特性矩阵对电网信息物理系统中信息流与能量流的复杂耦合关系和交互机理进行梳理与建模，用以描述电网信息物理系统中物理层、信息层及其相互之间的逻辑关联关系及特性。文献[4]指出二次系统具有信息物理高度耦合频繁交互的特征，采用有限状态机及混合逻辑动态模型两种混合系统模型形式对信息层与物理层进行描述。上述方法主要侧重于研究信息系统与电力物理系统建模方法，较少涉及二次系统故障位置的判断。

目前对智能站二次系统故障定位研究主要利用历史/实时运行信息、家族缺陷历史信息等确定系统运行状态[5-7]，其中文献[5]完成了继电保护通信系统的故障定位。文献[8]根据保护启动、保护动作、断路器跳闸、故障位置信号之间的逻辑关系，构建描述各信号之间关联的解析模型，将信号的实际状态和期望状态的最大匹配作为优化目标，利用优化结果检测继电保护装置隐性故障。而二次系统故障范围广泛，其故障分析及定位面临数据规模大、故障机理复杂、模型需求多样化的问题，广泛适用于二次系统状态信息间丰富的耦合及约束关系的故障定位方法仍然较少。配电网配备大量智能终端，与智能变电站信息物理系统类似，可借鉴配电网故障定位方法，其中矩阵算法具有较好的应用前景。文献[9]利用矩阵算法进行故障初步定位，并利用优化算法得到最终的定位结果，以实现配电网故障定位的快速准确判别。文献[10]通过分析配电网的拓扑和故障行波的传输路径，建立故障分支判定矩阵，得到故障分支判定原理与定位方法。矩阵算法具备建模直接、定位高效等优点，但若故障状态下二次系统约束关系相似可能造成误判。人工智能技术能够拟合非线性映射关系，有效提高故障识别精度[11，12]。神经网络中BP神经网络(Back-Propagation Neural Network)具有非线性映射的特征和良好的泛化能力，可利用其提高二次系统故障定位准确性。

为此，提出一种基于矩阵算法和BP神经网络的二次系统故障定位方法。首先基于IEC61850标准对实际变电站二次系统信息物理系统的交互逻辑进行梳理与抽象，得到变电站二次系统逻辑节点描述模型和二次系统状态解析式，并将二次系统状态解析式作为矩阵判据。然后，在获取二次系统拓扑关联和交互信息后利用矩阵算法能够快速确定可疑故障范围并作为输入集输入已训练好的BP神经网络得到精确定位结果。最后，以一起500kV开关误跳闸事故为例，验证方法的合理性和有效性。

1 二次系统矩阵化建模

以信息物理系统视角，首先从物理域、信息域2个维度对智能站二次系统的属性进行解析。物理域对象是站控层、间隔层、过程层的智能设备，其属性包括设备类型、拓扑结构、运行方式等；信息域对象是站控层、间隔层、过程层网络，及智能变电站管理系统，其属性包括通信方式、功能集合等。针对信息-物理的复杂耦合关系与交互机理，连通状态矩阵和逻辑节点描述模型可用于定量描述物理域、信息域关联关系与交互逻辑。

1.1 二次系统连通状态矩阵

智能站配置描述文件配置了通信网络功能参数和全站满足IEC61850协议标准的智能电子设备配置信息[13，14]。在IEC61850协议中，逻辑节点是交换数据的最小单元，其代表了物理装置内的某项功能，或执行这一功能的某些操作。因此以逻辑节点为最小单元建立连通状态矩阵，通过分析智能电子设备配置信息，得到二次设备内部逻辑节点信息交互过程，并用连通状态矩阵表示逻辑节点信息交互关系[15]。连通状态矩阵除依赖于逻辑节点之间的静态拓扑连接关系，还依赖于二次设备的当前状态。

建立连通状态矩阵A，描述逻辑节点间的连通关系以及连通状态，n为逻辑节点数，形式如式(1)。

(1)

式中：aij表示从节点i向节点j的连通状态；aij=1表示从节点i向节点j能够完成数据传输；aij=0表示从节点i向节点j无法完成数据传输；n为变电站二次系统中逻辑节点的数量。A中不同逻辑节点的aij取值所代表的连通状态根据逻辑节点描述模型确定。

1.2 逻辑节点描述模型

逻辑节点中包含了二次系统运行的测量、控制以及状态等信息[16]，以逻辑节点为最小单元建立的逻辑节点描述模型能够描述各类状态信息的属性、取值、来源、用途等，其中逻辑节点描述模型里的内容可以通过解析SCD文件获得。二次系统逻辑节点描述模型能够基于信息传输路径源宿信息一致性原理，实现二次回路状态故障定位；能够基于保护动作信号实现保护动作监测。不同类型的逻辑节点可以用不同的字符串表示，具体如表1、表2所示。

表1 逻辑节点状态描述模型

表2 逻辑节点在连通状态矩阵中描述模型

1.3 基于矩阵算法的故障定位方法

在获取到连通状态矩阵A之后，可通过设置故障修改其矩阵元素，形成新的连通状态矩阵，定义为故障连通状态矩阵A*，描述故障时变电站中逻辑节点之间的连通状态。当故障发生时，逻辑节点间关联关系和交互逻辑会改变，在连通状态矩阵中表现为矩阵元素值的变化，因此故障连通状态矩阵模拟智能变电站二次系统的一种故障情况。再经连通推理、根据二次系统状态解析式对故障定位方案进行校验，才能确定故障连通状态矩阵的有效性并判定故障范围。

故障连通状态矩阵建立的方法为：首先确定故障节点数k(n≤k≤m)。然后从连通状态矩阵A中选择k个元素，若元素aij=1则令aij=0；若元素aij=0则令aij=1，表示二次系统的逻辑节点信息交互关系由于二次系统故障发生变化，由此建立故障连通状态矩阵A*。其中，m和n为预先设定出现异常的逻辑节点间信息交互数目的上下限。n一般设为1，从遍历最小故障规模的单个逻辑节点间交互异常开始到遍历最大故障规模m个逻辑节点间交互异常结束，根据大量智能变电站二次系统故障案例总结出m取值1到3，在具体实现时可修改。

故障连通状态矩阵建立后，需利用基于连通推理的矩阵算法得到该定位方案下最终二次系统逻辑节点的状态。

不经过任何其他节点的连接，仅通过本节点对其他节点的直连回路通道对其他节点进行影响，称为一次连通推理。例如保护类逻辑节点故障向出口类逻辑节点发送保护启动和跳闸信息，出口类逻辑节点开始向开关量采集类逻辑节点发送跳闸报文，进行一次连通推理则出口类逻辑节点状态由0变为1，可表示为式(2)所示。

sign[X×A*]=B

(2)

其中，X为二次系统输入状态向量；B为X经过一次矩阵计算得到的变电站二次系统状态行向量。X由二次系统故障时各逻辑节点的初始状态确定，如式(3)所示。

(3)

其中，元素xi代表逻辑节点i的初始状态，由表1逻辑节点状态描述模型决定。

二次系统故障过程推演需进行多次矩阵计算，矩阵计算代表的实际意义主要包括节点间信息采集、命令执行、信息决策和控制指令下传递等过程[17]，最终得出二次系统各逻辑节点的状态，并用D表示如式(4)所示。

D=sign[sum(B)]

(4)

其中，B为X变电站二次系统的节点状态行向量，B中元素的意义由表1逻辑节点状态描述模型决定；sum(B)表示将所有矩阵计算得到的B进行矩阵加法运算；sign[z]为符号函数，当z>0时，sign[z]=1，当z=0时，sign[z]=0。

根据二次系统工作原理与逻辑节点的最终状态等信息建立二次系统状态解析式，用来描述各逻辑节点是否收到或发出报文、报告等消息。在通过矩阵计算得出的节点状态矩阵D后，利用状态解析式判断本次推理得出的二次系统各节点的状态是否与实际故障后节点状态相同，从而判断故障连通状态矩阵是否有效，作为二次系统故障定位的矩阵判据。

定义二次系统状态解析式如式(5)所示。

(5)

因此，可得式(2)的具体矩阵展开形式如式(6)、式(7)，两式表达了如何在给定二次系统故障前各逻辑节点的状态以及节点间连通状态这2个信息的情况下，通过直连回路通道实现逻辑节点间信息交互，计算推理其他逻辑节点状态。

(6)

bi=sign[x1a1i+x2a2i+…+xnani]

(7)

其中，bi表示逻辑节点i的当前状态；xi表示逻辑节点i的初始状态。

连通状态矩阵A和一个故障连通状态矩阵A*所有差异元素在矩阵中的位置信息用一个集合表示，如式(8)所示。

{(x1,y1),(x2,y2),…,(xi,yj),…,(xn,yn)}

(8)

其中，n为连通状态矩阵A和故障连通状态矩阵A*中差异元素的总数，(xi，yi)表示连通状态矩阵A和故障连通状态矩阵A*中第xi行第yi列元素存在差异，代表实际二次系统逻辑节点xi向逻辑节点yi的连通状态出现异常，与正常工作状态不符，属于可疑故障区域。

综上，在已知连通状态矩阵A及故障时输入状态向量X的情况下，只需进行多次矩阵计算，即可得到智能站二次系统中逻辑节点的状态，再结合二次系统状态解析式完成初步故障定位。具体方法如下：

步骤1：根据逻辑节点信息交互关系建立连通状态矩阵A，根据二次系统故障时各逻辑节点的初始状态建立输入矩阵X、二次系统状态解析式d，设定修改规则中修改元素数目上下限m和n。

步骤2：建立故障连通状态矩阵A*。

步骤3：按式(2)进行连通推理计算得到B。并将计算出的B作为X带入式(2)进行多次连通推理计算直至B不再变化。

步骤4：根据式(4)得到D。

步骤5：检查D是否符合二次系统状态解析式，确定故障连通状态矩阵A*是否有效。遍历所有的故障连通矩阵A*。并将所有有效连通状态矩阵A*按式(8)形式输出，作为矩阵计算故障定位结果。

2 矩阵算法-BP神经网络相结合的二次系统故障定位方法

2.1 BP神经网络模型

上述基于矩阵算法的故障定位方法具有规则简单、计算方便的特点，但涵盖的信息较单一，可能出现一个二次系统事故诊断出多个故障定位结果。BP神经网络能够精确逼近任意非线性函数，具有良好的系统学习能力。为此，在基于矩阵算法完成初步故障定位的基础上，采用BP神经网络进一步准确判定故障位置。

2.1.1 BP神经网络模型

人工神经网络一般由输入层、隐藏层和输出层构成，每个神经元将加权后的输入与阈值(偏移)向量代数求和后得到各自的输出。BP神经网络可通过构建误差逆向传播环节，使得实际输出值与期望输出值间误差最小[18]。

训练BP神经网络模型主要分以下三个步骤：

(1)构造网络模型，包括确定输入/输出数据形式、网络层次及传递函数形式。

(2)循环计算，正向传播计算误差，反向传播调整参数。

(3)返回训练好的神经网络模型。

本文采用的单隐藏层BP神经网络模型如图1所示，整体由三层网络组成，分别为输入层、隐含层和输出层。激活函数采用双曲正切tanh函数，如式(9)所示，输出层神经元传输函数如式(10)所示。

(9)

f(x)=1-y2

(10)

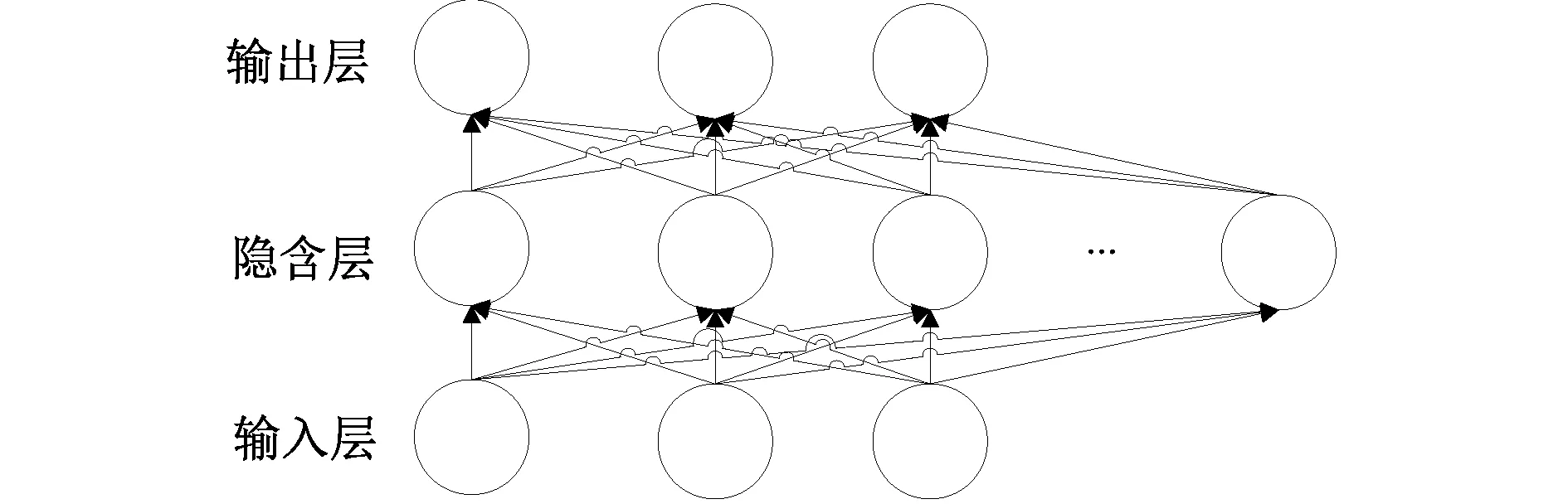
图1 三层BP神经网络模型Fig. 1 Model of Three-layer BP neural network

采用累计误差逆传播BP神经网络算法与标准BP算法区别在于读取一轮训练数据集T之后才对参数进行一次更新，能够避免标准BP算法参数更新频繁的弊端，其最小化的目标为训练数据集上的累计误差如式(11)、(12)。

(11)

(12)

其中，Ek为网络在单个训练样本上均方误差；E为累计误差逆传播算法的最小目标函数；N为训练数据集样本总数；m为样本维度；zk*(j)为根据神经网络当前参数计算得到的样本输出；zk(j)为原训练集的样本输出。

2.1.2 数据样本的构造

数据样本输入来源为矩阵计算得到的故障节点坐标集合，但要将故障节点的位置信息转化为序列形式，作为BP神经网络的输入。

例如连通状态矩阵A为3维方阵，n=1，m=3，则矩阵算法故障定位结果式(8)中的x、y元素对应的序列编码如表3所示。BP神经网络故障定位结果的编码含义如表4所示。

表3 矩阵算法故障定位结果中位置信息编码

表4 故障定位结果编码

输入输出都规定为编码形式，无需再进行数据归一化处理。计算出的故障连通状态矩阵A*数目最多为2，若故障连通状态矩阵A*数目不足2，则编码序列末尾补0，保证输入层序列长度相等。部分原始数据和样本数据形式如表5、表6所示。

表5 样本举例

表6 处理后的样本举例

2.2 矩阵算法-BP神经网络故障定位方法基本流程

首先根据1.3节基于矩阵算法的故障定位方法得到初步故障定位结果，再将其作为BP神经网络的输入，根据BP神经网络的输出得到最终诊断结果，故障定位总体流程如图2所示。

图2 矩阵算法-BP神经网络故障定位方法流程图Fig. 2 Flow chart of matrix calculation BP neural network fault location method

3 案例分析

3.1 案例简介

以一起500kV开关误跳闸事故为例分析，利用Python语言编程推理得到故障诊断结果。在500kV FX甲线受到区外扰动时，XW站5001、5012开关跳闸，发生故障电网与主网解列，其中5012为桥接开关。500kV FX甲线复电试送过程中，当XW站合上 5001开关对FX甲线充电时，5001开关再次跳闸。跳闸前运行方式如图3所示。XW出线线路保护配置情况如表7。

图3 跳闸前运行方式示意图Fig. 3 Schematic diagram of operation mode before tripping

表7 XW站出线线路保护配置情况

第一次跳闸前，XG甲、乙线、FX甲线正常运行，XW站5001、5002、5012开关在合位。

第一次开关跳闸时，500kV 线路保护、断路器保护无动作报文，录波器未监视到跳闸信号，开关操作箱第一组跳闸灯亮，5001、5012断路器保护装置A、B相收到跳闸失灵启动开入变位，持续11 s。5001和5012开关操作继电器箱的第一组跳闸#1线圈的A、B两相指示灯点亮。根据跳闸时刻的录波和信号，初步判断跳闸命令来自FX甲线主一或主三保护装置。

为尽快恢复故障电网与主网联网，在XW站开关站更换500kV FX甲线主一保护装置插件并全面检查后，又退出了主三保护出口和功能压板。利用5001开关对FX甲线试送。试送后，5001开关再次跳闸。第二次跳闸，500kV线路保护无动作报文，录波器未监视到线路保护跳闸信号，5001 断路器保护动作，开关操作箱第一组、第二组跳闸灯亮，5001断路器 A、B相收到跳闸失灵启动开入变位，持续11 s，且PRS-753型号线路保护跳闸脉冲为11 s。第二次跳闸，5001断路器保护沟通三跳出口动作跳闸。

3.2 故障定位模型建立

对案例所涉及的逻辑节点进行编号，如表8。

表8 逻辑节点编号

根据第一次跳闸保护配置情况，出口类逻辑节点FX甲线主一、主三保护出口PTRC可以向开关量采集类逻辑节点5001、5012开关操作箱XCBR发送跳闸报文，建立连通状态矩阵A1如式(13)所示。

(13)

(14)

根据第二次跳闸保护配置情况，建立连通状态矩阵A2如式(14)。通过故障分析报告、二次设备运行记录及相关文献资料形成数据集[19]。针对单个节点故障类型建立数据集样本数为3300。本案例只考虑单节点故障，即n=m=1，连通状态矩阵A为13维方阵，且最多计算出的A*数目设为2。

3.3 故障定位模型参数优化

将上节建立的3300条二次系统数据集，以8∶2的比例建立训练集和测试集，形成训练数据集T。本文采用的BP 神经网络共三层，其中输入层节点数为52，隐藏层节点数为5，输出层节点数为2；初始输入层权重和偏置值服从[-0.2，0.2]区间上的均匀分布，初始输出层权重服从[-2，2]区间上的均匀分布；训练过程中输出层的神经元最大值对应位置元素为1，其余为0。对于初始学习率、隐藏层数的调整，以训练样本集的判断准确率作为网络参数的优化指标，对于迭代次数的调整，以训练样本集的累计误差作为网络参数的优化指标。

表9为不同初始学习率、隐藏层数的BP 神经网络的故障定位准确率。可知，经300次迭代后，初始学习率为0.01、隐藏层数为5的神经网络优化效果最佳。图4为初始学习率为0.01、隐藏层数为5的BP 神经网络的训练损失。由图4可以看出，当训练轮数达到200轮后，训练损失趋于稳定。

表9 迭代300次后的网络优化情况

图4 BP神经网络训练损失Fig. 4 Training loss of BP neural network

使用原二次系统数据集，分别以7∶3、8∶2、9∶1的比例建立相对应的训练集和测试集，形成新的训练数据集T1-T3。训练时，输入层节点数为52，隐藏层节点数为5，输出层节点数为2，学习率为0.01，共训练200轮。为比较文中所提BP神经网络模型的准确率，选取循环神经网络模型和标准卷积神经网络模型对相同的样本集进行训练和测试[20]，训练次数均为200次。表10为所提BP神经网络模型、循环神经网络模型和卷积神经网络模型在相对应的训练集和测试集上二次系统故障数据的诊断结果。

表10 不同模型的诊断准确率

由表10可以看出，BP神经网络模型在不同的测试集下均保持了较高的故障诊断准确率，平均准确率达到了89.1%，并且在每个测试集上的诊断效果较为稳定，均保持在86.8 %及以上。

3.4 故障定位分析

案例中第一次跳闸为区外故障，只有故障源节点状态值取1，故障输入状态向量如式(15)所示。

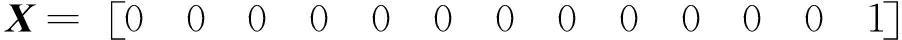
(15)

XG甲线主一保护出口和FX甲线主三保护出口有跳闸信号根据第一次跳闸时保护动作情况建立第一次跳闸情况的二次系统状态解析式d1如式(16)。

(16)

(17)

(18)

(19)

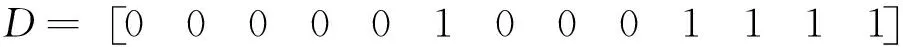
(20)

当故障状态矩阵A*为式(17)时，按式(2)经一次矩阵计算得到B(1)如式(18)、按式(2)经过三次矩阵计算得到B(3)如式(19)，计算停止。按式(4)计算得到D如式(20)所示，满足二次系统状态解析式d1，则故障连通状态矩阵A*有效。

通过矩阵推理计算最终得到只有式(17)的故障连通状态矩阵A*有效，与式(13)连通状态矩阵对比，只有第13行10列元素变化，因此得到故障定位结果如式(21)所示。

{(13,10)}

(21)

将定位结果按2.1.3节转换成编码序列并输入到已训练好的BP神经网络，得到输出为10，依照2.1.3节数据样本构造原则可知，第一个集合{(13，10)}代表的故障类型为故障定位结果，表示FX甲线主三保护出口PTRC故障。现场开关跳闸原因为现场直流电源异常，引起FX甲线主三保护(为PRS753B型号装置)出口回路驱动器的总线状态保持回路保持了异常电平，且出口板放大了异常导通电流，从而导致区外扰动时继电器出口，出口回路驱动器属于FX甲线主三保护出口PTRC。故障定位结果与现场二次回路检查一致。

案例中第二次跳闸的故障输入状态向量与第一次跳闸时相同，如式(15)所示。根据第二次跳闸时保护动作情况建立二次系统状态解析式d2如式(22)。

(22)

通过矩阵计算得到故障定位结果如式(23)。

{(13,6)},{(13,11)}

(23)

将定位结果按2.1.3节转换编码序列并到已训练好的BP神经网络，得到输出为10，依照2.1.3节数据样本构造原则可知，第一个集合{(13，6)}代表的故障类型为故障定位结果，代表XG甲线主一保护出口PTRC故障。现场开关跳闸原因为现场直流电源异常，引起FX甲线主一保护(为PRS753B型号装置)出口回路驱动器中总线状态保持回路保持了异常电平，且出口板放大了异常导通电流，从而导致区外扰动时继电器出口。出口回路驱动器属于XG甲线主一保护出口PTRC，定位与现场二次回路检查一致。