解答初中物理问题的几种特殊思维策略

阚小勇

(江苏省如皋市江安镇滨江初中 226534)

物理学习作为一种有意义的学习，学生必须解答大量的物理习题以加深对物理概念、规律及物理思想方法的理解.物理解题的过程也是主体积极认知的过程，解答物理习题涉及到人如何获取信息、加工信息，如何进行决策思维，以及如何储存和提取知识等等.为提高学生解答物理问题的能力，在物理教学过程中必须教给学生一些特殊的解题思维策略.所谓物理习题的解题策略，是指在探求物理习题答案的过程中所采取的途径和方法，它是对解题过程的概括性认识.而特殊思维策略，是指思考路径不太常规，而对解题活动又能出奇制胜的思维策略.现结合具体习题的解答谈几种特殊思维策略的应用.

1 变更问题策略

所谓变更问题策略，就是主体面对难以完成知识的提取和推理而无从下手的问题时，思维不要停留在原问题上，而是思考原问题的情境是否可以进行“反客为主”的变更，能否换一种表述方式来把它改变成一个等价问题，使它变得更熟悉、更简单、难度大大降低而更加易于解决的新问题，以便通过解决其等价问题而达到解决原问题的目的，这显然有助于提高学生思维的变通性与创造性.

例1 某游客去泰山旅游，第一天早上9∶00检完票进入景区大门沿山路步行爬山，于下午14∶00到达山上某一宾馆住宿，在第二天早上9∶00时又从该宾馆处下山沿原路步行返回，正好于下午14∶00离开景区大门，则在该线路上____(选填“不一定”“一定”或“一定不”)存在这样一个地点：该游客第二天返回经过该地点的时刻与第一天经过该地点的时刻相同.

解析本题采用变更问题法，在不改变问题实质的情况下，恰当引入一个替代过程，可使原问题变得易于求解.题中给出的条件是同一个人在前后两天走过相同的路程，现假设在第二天这个游客从宾馆出发返回景点大门的过程中，有另一个“替身”游客模拟该游客第一天的行为从景点大门走向山上宾馆，因为他们出发的时刻相同(均为早上9∶00)而又相向而行，所以他们必然会相遇在宾馆与景区大门路途之间的某一位置，而且相遇时所经历的时间也必然相等，答案显然是“一定”存在这个地点.

2 代入检验策略

有些问题通过正面求解也许不能得出正确答案，而问题本身存在几个可能的答案，用常规的逻辑推理难以排除这些可能答案中的错误选项时，可以采用相应的物理知识，写出相关量之间的关系式后，将题给选项逐一代入这个关系式进行检验，使关系式成立的选项即为所需答案，这种代入检验策略有时是很奏效的.

例2 有甲、乙两种物质制成的两个物体，它们的质量之比为3∶1，吸收的热量之比是2∶1，则它们升高的温度之比和比热之比分别为( ).

A.2∶3，10∶1 B.5∶3，2∶5

C.3∶2，1∶10 D.3∶5，5∶2

解析这里先用“等分量”法设甲、乙两物体的质量分别为3m和m，吸收的热量之比分别为2Q和Q，比热之比为c甲和c乙，升高的温度之比分别为Δt甲和Δt乙，则根据吸热公式Q=cmΔt可得：

2Q=c甲×3mΔt甲

①

Q=c乙×mΔt乙

②

联立①②得：

③

将各选项分别代入③式，只有选项B正确.

3 模式识别策略

在物理解题活动中，解题主体通常都是首先辨别题目的类型或所涉及到的物理知识，以便与已有的知识发生联系，从而迅速从记忆中提取有关知识来解决问题，这种解题策略叫做模式识别.如果很快识别出这个问题属于哪一类，就能由此选择大致的解题方向，缩小搜索的范围，提取相关知识进行求解，问题的解法和答案也会很快的明朗起来.

例3 某同学在使用托盘天平称量一个物体的质量时，先把天平放在水平台上，由于疏忽而没有把游码拨回“0”刻线处，当游码位于0.2克处时去调节平衡螺母，使指针指到刻度盘的正中央，之后把被测物体放在左盘，在右盘中加入43克砝码时，天平再次恢复平衡，由此可知被测物体的质量为( ).

A.43.0克 B.43.1克

C.42.9克 D.不能确定

解析天平本身是个等臂杠杆，当天平放在水平台上指针指在刻度盘的中央而使横梁处于平衡状态时，左盘中物体的质量与右盘中砝码的质量是相等的，所以本题答案为A.显然，这里只要能识别出天平的工作原理就能得出正确答案，至于题中游码位于0.2克处时对天平所形成的影响，其实已被调节平衡螺母所抵消，这与游码位于“0”刻度线处时去调节平衡螺母使横梁平衡并没有本质区别.当然，此时若需要向右移动游码才能使横梁平衡，则物体质量应为m法+(m游-0.2克)，其中m游为游码所对刻度值.

4 以退求进策略

解题时先退到我们最容易看清楚问题的地方，认清了，看透了，钻深了，然后再去解决问题，这就是“以退求进”的策略.运用这一策略常见的情形有：从一般退到特殊；从复杂退到简单；从多退到少；从整体退到局部；从较强的命题退到较弱的命题.使抽象的问题具体化，以便使其中的数量关系或空间形式更明确，也就更容易找到解题的途径.

图1

A.杠杆将失去平衡，右端会上升

B.杠杆将失去平衡，左端端会上升

C.杠杆始终保持平衡

D.无法判断

解析本题的问题是“蜡烛燃烧的过程中”，可将这个条件退到特殊情况，因为蜡烛A、C较短，不妨选择蜡烛A、C同时烧尽的时刻来分析，则此时蜡烛B还剩下一半，此时杠杆将失去平衡，且右端会上升，所以正确选项是A.

5 先进再退策略

这种解题策略与“以退求进”策略的思路恰好相反，即在解决一个特殊问题时，先将这个问题作一般化的探讨，推进到一般情况来考虑问题，通过对一般问题的解决，再返回来解决原来给出的问题，以达到最终解决问题的目的.

A.0.28安 B.0.33安 C.0.11安 D.0.22安

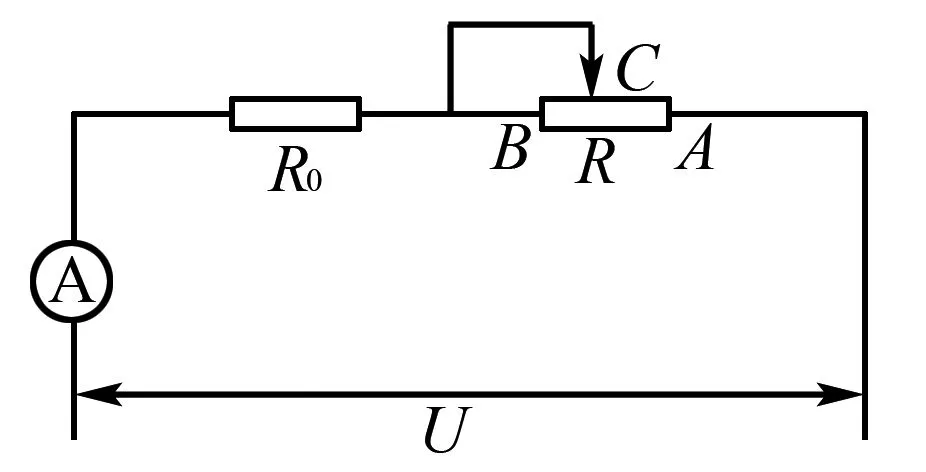
图2

解析本题通常用欧姆定律列出方程求解，但若能将问题作一般化的处理.将定量计算的问题转化为定性分析问题，这里采用“逆向思考”的方法来分析.若把滑片向左移动到B点，滑动变阻器接入电路的电阻最大，电路的总电阻最大，电流最小；当滑片向右移动时，变阻器接入电路的电阻减小而导致总电阻减小，电流必然增大而大于开始时的0.3安，所以答案只能是B.这样就免去了列式求解的繁琐.

6 正难则反策略

对某些物理问题，若从正向(由因到果)的思路去寻找解题路径时可能难以解决，此时若转而从反向(由果到因)的思路去考虑，以突破思维定势，使陷入僵局的思维进入新的境界而很快就能得出结论，这种对问题从正面解决有困难而转向反面寻求解法的思维策略称为“正难则反”策略，也可称为逆向思维策略.使用这种策略解题往往能达到“柳暗花明又一村”的效果.常见的几种方法是：分析法、反证法、淘汰法和逆推法.

例6 如图3所示的电路中，R1、R2为定值电阻，若电源电压恒定，开关闭合后，将滑动变阻器的滑片P向右移动，则( ).

图3

A.电流表示数变小，电压表示数变小

B.电流表和电压表示数都变大

C.电阻R1消耗的功率增大

D.整个电路消耗的总功率不变

总之，我们在平时的教学过程中，要有意识地指导学生加强对解题策略的总结，积累一些特殊的思维策略，并学会灵活地运用这些策略来解决问题，以达到迅速、准确地解题的目的，也能优化学生的思维品质，提升创造性解题的能力.