一种针对聚类问题的量子主成分分析算法
2022-12-16刘文杰王博思陈君琇
刘文杰 王博思 陈君琇
1(数字取证教育部工程研究中心(南京信息工程大学) 南京 210044)2(南京信息工程大学计算机与软件学院 南京 210044)(wenjie@163.com)
聚类是将一组物理抽象对象分类为由相似对象组成的不同类别的过程.聚类产生的集群是一组数据对象,同一集群中的对象相似程度高.因此,聚类研究的是样本在尺度空间上的分布.在聚类问题[1-2]上,聚类样本数据中的离群点容易影响簇中心的选择,进而影响聚类结果,且样本点规模的扩大会造成算法需要在样本点间的距离计算上消耗大量计算资源,这些都导致算法在复杂度和精度上存在一些不足.为了研究量子计算在聚类问题上的应用与扩展,Horn等人[3]提出量子聚类(quantum clustering, QC)算法.不同于经典的K-Means[4]和K-Medians[5]算法,QC算法在迭代过程中用于聚类的度量距离相对固定,学习速率不容易确定.2007年,李志华等人[6-8]对QC算法进行了改进,提出了基于距离的量子聚类算法,该算法解决了QC算法在迭代过程中的缺陷.此外,Zhang等人[9]通过指数距离函数对QC算法中样本点间距离计算方法和迭代过程作出改进,提出了新型量子聚类算法,EDQC算法.但上述算法的簇中心的选取很容易受到离群点以及聚类规模的影响,当待聚类的样本点线性不可分时,这些算法聚类效果并不是很好.
针对聚类问题,本文提出了一种新型的量子主成分分析算法——QPCA算法(quantum principal component analysis algorithm),结合奇异值分解[10]的思想,用于提取待聚类数据的主成分,以便选取更为准确的簇中心.此外,本文采用了Liu等人[11]提出的量子最小值搜索算法,通过优化不同样本点之间距离最小值搜索过程,降低聚类的迭代次数.实验部分采用Cirq[12]量子编程框架进行量子仿真验证,由于可使用的量子比特位数的限制,本文完成了小规模数据集情况下的量子实验的验证.
本文工作的主要贡献有3个方面:
1) 提出采用新型量子主成分分析算法,选取更为准确的簇中心,减少异常值对簇中心选择的影响;
2) 利用指数距离公式计算样本点到簇中心的距离,同时采用量子最小值搜索算法加快最短距离搜索,减少聚类所需迭代次数;
3) 采用Cirq量子编程框架完成相关量子仿真实验,比已有的传统及量子聚类算法、QC-PCA算法在聚类准确度和性能上都有不同程度的改进.
1 相关工作
本节中主要介绍主成分分析算法以及量子主成分分析算法的基本定义以及作用特点.
主成分分析(principal component analysis, PCA)算法[13-14]常用于数据分析,能够在保持数据集主要信息的同时降低数据集的维数(特征的数量).
量子主成分分析(QPCA)[15-18]是一种将量子计算与传统机器学习结合的量子降维算法,能够获取数据矩阵中最具有代表性的特征值对应的特征向量并进行重构. 具体的算法过程为:
假设存在具有n个样本点且每个样本点具有m维特征的数据集用矩阵X=(xn)来表示,每个样本点可以被表示为xi=(xij),1≤i≤n,1≤j≤m,σ代表奇异值.
初始态制备阶段应用2个酉操作:
UM:|i〉|0〉
(1)
UN:|0〉|j〉
(2)
其中
酉操作UM和UN分别用于编码并得到初始样本点的量子态形式以及在幅度上编码样本点范数.X*为X的伴随矩阵.利用式(1)、式(2)这2个酉操作能够帮助操纵量子比特,得到需要的初始态:
|ψs〉=UMUN|0〉|0〉=
(3)
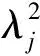
(4)
σj表示奇异值.而量子态能够被表示为
(5)
其中|uj〉和|vj〉分别保存着矩阵的左奇异向量和右奇异向量.通过额外增加辅助量子位,求解密度矩阵的幂,并且对幺正运算W执行相位估计:
W=(2MM†-IND)(2NN†-IND)=
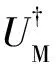
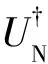
(6)
得到
(7)
(8)
执行逆相位估计,将特征值寄存器释放,执行受控旋转操作CR(β1),CR(β2),…,CR(βd),得到:
CR(βj):|j〉|0〉
(9)
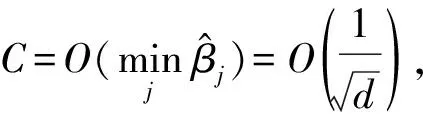
(10)
经过投影测量最终可以得到:
(11)
经过上述步骤,存储所有数据点信息的量子态|ψs〉被转换成低维的量子态|ψe〉:
|ψs〉|ψe〉
(12)
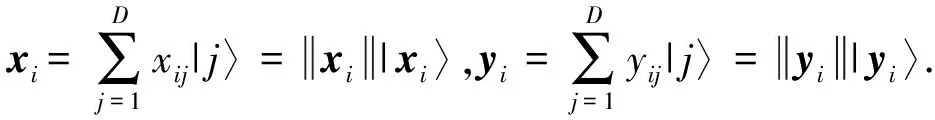
2 针对聚类问题的量子主成分分析算法
针对聚类问题,本文提出了QC-PCA算法.先将待聚类的原始数据集矩阵进行奇异值分解,利用预设的阈值更新奇异值并得到主成分,对原始数据集特征进行筛选和提取,再利用薛定谔方程表示筛选后的数据特征,分别采用波函数和势函数描述数据分布状态和势能大小,从而减少异常值对簇中心选取的影响,选取具有代表性的簇中心.此外,采用量子最小值搜索算法[11]寻找距离样本点最近的簇中心,减少聚类所需迭代次数.重复上述步骤,遍历所有样本点并完成聚类.本文提出的算法过程可以用算法1来描述.
算法1.QC-PCA算法.
输入:N个数据、维度M、k个聚类、阈值τ;
输出:样本聚类结果.
① 准备量子态:|ψ1〉=|0〉|0〉L|0〉C|ψs〉B;
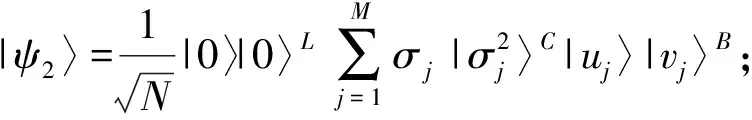
④ 选取k个簇中心ci,i∈[1,k];
⑤ fori=1,2,…,N-kdo
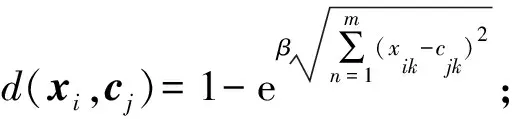
⑦ 搜索样本点到簇中心的最小距离,聚类;
⑧ end for
⑨ 计算各类的质心作为新的簇中心;
⑩ 重复迭代⑤~⑨直至前后簇中心相同,完成聚类.
假设存在具有n个样本点且每个样本点具有m维特征的数据集用矩阵X=(xn)来表示,每个样本点可以被表示为xi=(xij),1≤i≤n,1≤j≤m,σ代表奇异值,δ,k,τ分别表示测量距离,聚类类别以及预设的阈值.QC-PCA算法能够通过6个步骤来进行描述:
步骤1.量子态准备.
利用UM,UN这2个酉操作分别编码并得到初始样本点的量子态形式以及在幅度上编码样本点范数,产生想要的初态.制备处于|0〉量子态的量子比特,通过式(3)得到最终的量子态为|ψ1〉=|0〉|0〉L|0〉C|ψs〉B.
步骤2.奇异值分解.
步骤1得到的初态能够采用主成分分析的思想进行奇异值分解,得到前d个表示数据主要特征的量子态形式的主成分|v1〉,|v2〉,…,|vd〉,它们相应的所占方差比例可以用式(4)表示.根据式(1)(2)(4),式(3)可以被化简为
(13)
通过额外增加辅助量子位,求解密度矩阵的幂,并且在第2个寄存器上利用式(6)对幺正运算W执行相位估计,得到量子态:
(14)
步骤3.更新奇异值提取主成分.

(15)
(16)
利用2种受控旋转操作消除了阈值变化,实现了高保真、高概率的矩阵逼近.量子主成分分析算法的整个电路设计如图1所示:
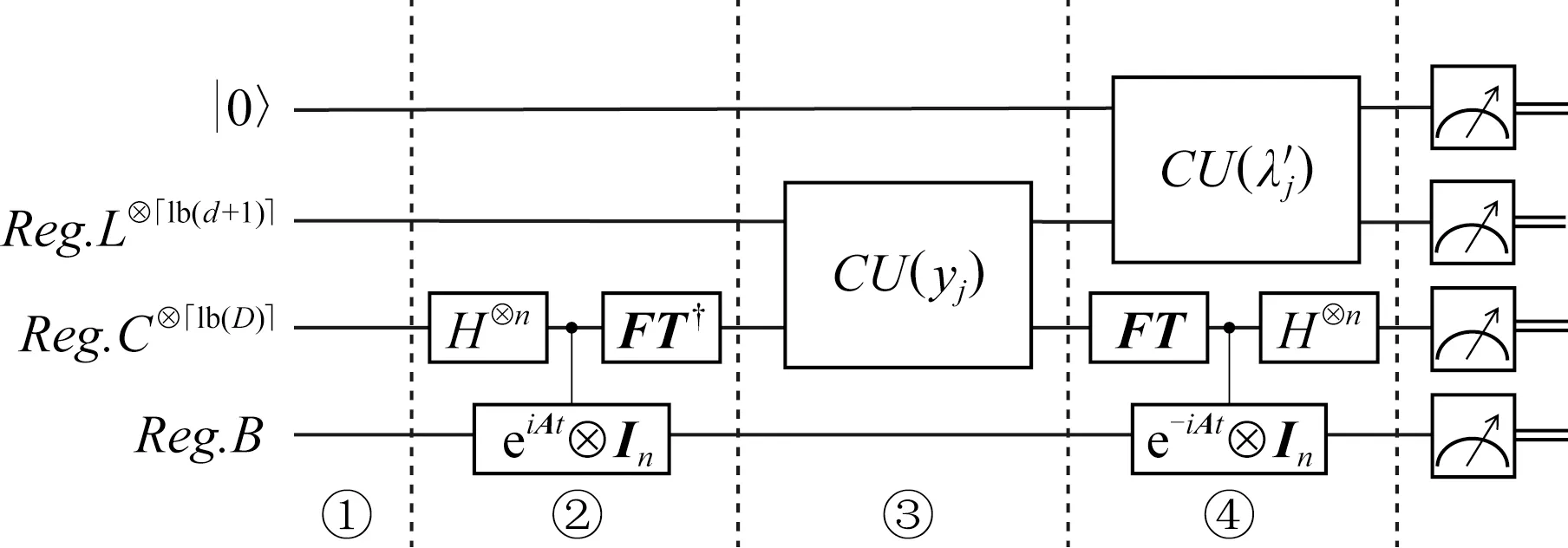
Fig. 1 Circuit of quantum principal components analysis algorithm图1 量子主成分分析算法电路
步骤4.选取簇中心.
筛选后的数据集样本点可以被描述为量子力学中的希尔伯特空间中的粒子,其分布能够用薛定谔方程表示为
(17)
其中H,V,E分别表示哈密顿算符,势函数以及H可能的特征值.利用势函数V可以写出特征态函数,也就是高斯波函数表示:
(18)
除此之外,在给定波函数Ψ时,利用Schrödinger方程也可以求解出决定样本点分布的势函数V,即
i∈{1,2,…,k}.
(19)
簇中心ci可以用从势能值集合中挑选出的k个最小值数据xi来表示.
步骤5.计算样本点到各簇中心距离.
随机挑选出一个样本点数据,利用指数距离公式
(20)
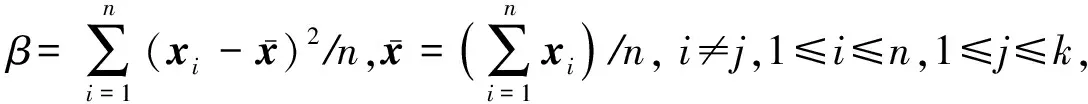
(21)
步骤6.聚类.
计算样本点到各个簇中心点的距离,并采用量子最小值搜索算法[11]找到最小距离,完成该样本点的聚类.重复步骤5的过程,直到所有的数据样本被聚类为k个类别.然后计算同类别数据点的质心作为新的簇中心,假设第i个聚类中有f(X,Y)个点,则新的簇中心为
重复步骤5以及步骤6直至前后2个簇中心相同,聚类结束.

3 实验仿真
3.1 实验设计
为了验证本算法的有效性和可行性,本文采用Cirq[12]量子编程框架实现小规模数据集下的量子算法验证.所有实验均运行在一台配置显存为40 GB的NVIDIA Tesla A100显卡,Intel GOLD 5220R CPU,256 GB内存的服务器上,编译语言采用Python,编译器采用Pycharm.

Table 1 Dimensional Features of Some Data Points to be Clustered

Fig. 2 Distribution of data points to be clustered图2 待聚类数据点分布
S0~S119为随机生成的120个样本点,F0~F5表示每个样本点具有6个特征.待聚类数据点分布示意图如图2所示,相同颜色深度的点代表生成的相同类别的数据.
3.2 实验流程及对比分析
首先根据数据集,利用UM和UN酉操作准备量子态:
|ψ1〉=|0〉|0〉L|0〉C|ψs〉B,
(22)
其中|ψs〉满足式(3).接着将|ψ1〉进行奇异值分解,并附加量子位,执行酉操作W的相位估计,得到量子态:
(23)
计算yj=(σj-τ)/σj=1-τ/σj,yj∈[0,1),执行受控旋转,根据旋转角度,利用受控旋转门将奇异值与阈值相减,筛选出d维大小的主成分,得到量子态:
(24)

(25)
此时对应原数据,得到筛选后的数据点以及对应的聚类类别如表2所示:
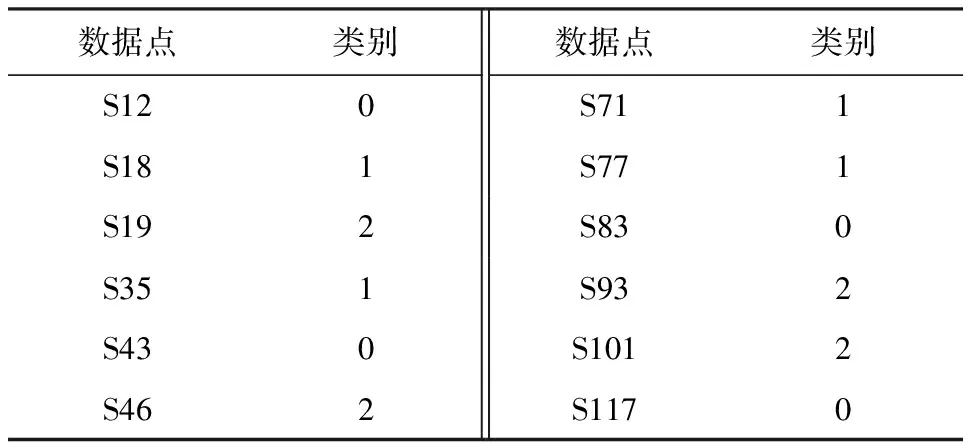
Table 2 Data Points Obtained from Selection
从势函数集合中选择3个最小值作为簇中心ci,i∈{1,2,3},实验得出S12、 S35样本、S93样本分别为该数据集聚类的3个初始簇中心.利用式(20)的指数距离公式对原始数据集进行距离计算,计算出每一个随机样本到这3个簇中心的距离.最后采用最小值搜索算法搜索出最小的距离,将此数据点分类到该类别中.直到所有样本数据点都计算完成,最终完成数据样本点的聚类分布.图4为最小值搜索算法的电路设计:

Fig. 3 Circuit of quantum minimum search algorithm图3 量子最小值搜索算法电路
现有的量子聚类算法采用Grover算法搜索样本点到簇中心点距离的最小值.当数据规模较小时,Grover算法的成功率不能达到100%.本文在搜索过程中采用的最小值搜索算法[11]基于Grover-Long算法做出改进,提高搜索成功率,并且采用动态策略降低算法的复杂度,同时优化设计电路,缩减门的数量.
随着现代通讯科技的快速发展,信息传递模式逐步呈现出多元化特征,而媒体运维的核心仍然是信息的基本内容。对于新闻资讯热点的筛选与信息表达方式的选择,能够有效反映一家新媒体的专业水平。时政新闻在新闻领域发挥着不可替代的作用,但部分电视媒体缺乏对其应有的重视,甚至肤浅的认为时政新闻的主体内容应当局限于领导决策层的重要会议,与基层群众的根本利益不产生关联。这种理念不仅是对党政战略指导方针的亵渎,也是对民生新闻的曲解。因此,确立宏观民生新闻理念势在必行,并且应当从如下几方面着手。
除此之外,本文在数据集统一的情况下,将提出的QC-PCA算法与QC算法、EDQC算法以及文献[20]提出的NSQC算法在聚类准确度(样本聚类正确的个数/总样本数)上进行比较,结果如图4所示.另外,图5展示的不同算法的聚类效果,图5(a)表示原始数据集样本点分布及所属类别,图5(b)~(e)分别表示QC,EDQC,NSQC以及提出的QC-PCA算法的聚类效果.从图4可以看出,经过10次迭代,4种算法的聚类准确度都趋于收敛,其中QC-PCA算法的聚类准确度最高,为0.78, NSQC算法的聚类准确度为0.75,EDQC算法的聚类准确度为0.74,QC算法的聚类准确度最低,为0.72.图5(e)代表的QC-PCA算法的聚类效果相对较好,相同类别的数据点的颜色相比较于其他聚类算法显得比较统一,图5(b)(c)(d)代表的QC,EDQC,NSQC算法的聚类结果相对较差,相同类别的数据点的颜色分布比较凌乱.
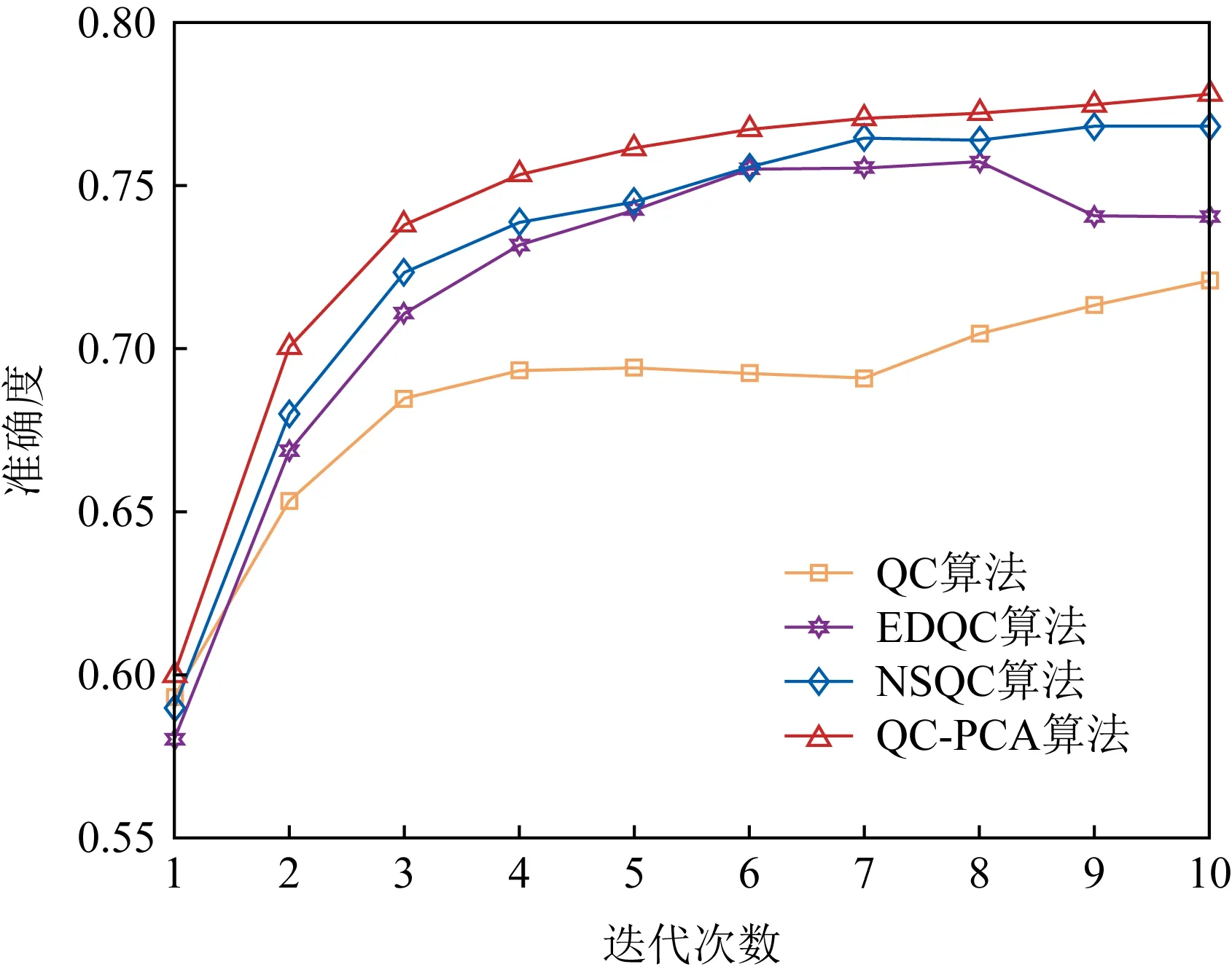
Fig. 4 Comparison of clustering accuracy for algorithms图4 不同算法的聚类准确度比较
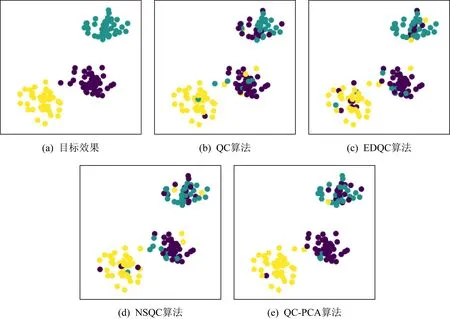
Fig. 5 Comparison of clustering performance for four quantum clustering algorithms图5 4种量子聚类算法的聚类效果比较
实验结果表明,本算法利用量子主成分分析算法对数据进行预处理,能够较为准确地选出具有更多主成分的数据点作为簇中心,降低了簇中心的选取对聚类精度的影响.另外,本算法采用优化后的量子最小值搜索算法,降低了样本点之间最短距离搜索的复杂程度.
4 性能评估
本节分别从簇中心选取和样本点之间最短距离搜索的时间复杂度以及资源消耗3个方面对提出的QC-PCA算法做出评估.假设存在N个M维的样本点数据,分为K类,迭代次数为T.
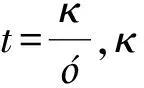
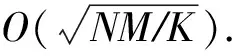
从资源消耗上来看,本文提出的QC-PCA算法与经典算法K-Means相比,从原来的O(NM)比特降到了O(logNM)量子比特,与其他量子算法相比,从O(NlogM)量子比特降到了O(logNM)量子比特.表3选取K-Means算法、QC算法、EDQC算法、NSQC算法、QC-PCA算法,从簇中心选取时间复杂度,最短距离搜索时间复杂度和资源消耗这3个方面给出了具体的对比和评估.

Table 3 Complexity Comparison for Different Algorithms
根据表3可以直观看出,QC-PCA与传统算法和其他3个量子算法相比在簇中心选取时间复杂度、最短距离搜索时间复杂度以及资源消耗上均有不同程度的改进效果.
5 总 结
本文提出了一种针对聚类问题的量子主成分分析算法(QC-PCA算法),利用奇异值分解的思想,减少异常值对簇中心选取的影响,并采用量子最小值搜索算法寻找距离样本点最近的簇中心,减少聚类所需迭代次数.仿真实验表明,QC-PCA算法与已有的量子聚类算法相比,提升了聚类准确度.性能评估表明,QC-PCA算法与已有的传统算法及量子聚类算法相比,在簇中心选取时间复杂度,最短距离搜索时间复杂度和资源消耗上均有不同程度的改进.
作者贡献声明:刘文杰是本研究的构思者,指导实验设计、数据分析、论文写作与修改;王博思是本研究的实验设计者和实验研究的执行人,完成数据分析,论文初稿的写作;陈君琇参与实验设计和实验结果分析.全体作者都阅读并同意最终的文本.
