可控、可追责的敏感数据共享方案

2022-12-16张正昊张振江

计算机研究与发展 2022年12期

张正昊李勇张振江

(北京交通大学电子信息工程学院北京 100044)(19120172@bjtu.edu.cn)

在当今大数据时代，人们的日常生活中会产生大量数据，这些数据代表着一个人的日常习惯、行为动态、生活轨迹等，是极其重要的隐私数据.数据产生的源头可能多种多样，不同的公司、企业、部门之间都持有用户数据.在大数据背景下，这些蕴涵着巨大价值的数据必然走向共享、开放[1]，即数据只有流动起来才能发挥其最大效能，进一步挖掘出数据背后的隐藏信息，为企业和个人提供更好的服务质量[2-3].如果不同数据只存放于独立的机构内部，就会形成“数据孤岛”，数据得不到充分利用，造成数据浪费.

然而，数据共享过程中存在的突出问题是，数据拥有方往往难以控制数据的流向，数据是否能得到合法使用也难以保证.例如2020年11月，国内某快递公司的40余万条客户个人信息被内部用户获取之后倒卖，被泄露的信息包括客户的收发件地址、姓名、电话等，这是一起严重的数据泄露事件.因此有必要研究隐私数据在各方之间共享时的安全性，实现数据的可控共享.另外，许多信息泄露事件都是内部人员所为，因此数据共享也需要设置监管方对数据共享进行监管，确保所有的数据获取请求和数据响应合规合法，最大程度避免数据泄露情况的发生.

1 相关工作

针对敏感数据共享过程中的痛点和难点，文献[4]基于大数据平台提出了一种安全的敏感数据共享框架.该框架从平台中数据的生命周期出发，分别从数据提交、存储、使用和销毁4个方面考虑数据的安全共享问题.文献[4]的作者设计了一种异构代理重加密方案，支持从身份基加密[5]到公钥加密[6]之间的转换.另外为了避免隐私信息的泄露，数据请求者将在基于虚拟机监视器(virtual machine monitor, VMM)[7]的私有进程中对数据进行下载操作，所有的密钥将保存在私有进程的内存中.框架为所有隐私数据设置了一种基于租约的机制，在租约到期后，明文和密钥将从云中彻底销毁.但是该框架对请求者的隐私问题考虑不充分，任何发生在平台上的数据共享行为都会被无关第三方得知，并且其访问控制功能的实现主要依赖于数据拥有方是否为请求方生成了重加密密钥，对数据请求方的权限控制相对较弱.

2008年，Nakamoto[8]提出比特币概念，区块链开始引起关注.由于区块链具有分布式、防篡改等特性，一些学者开始使用区块链进行访问控制，以设计可控的敏感数据共享方案.文献[9]针对云环境下的电子病历共享场景，设计了一个轻量可扩展的联盟链，所有的用户实体都将经过授权之后才能进入共享系统，并且所有的共享行为都会被实时记录.该方案利用区块链分布式与防篡改等特性，构造了比较强的访问控制方案.文献[10]研究了医疗数据在无信任环境下的数据共享问题，基于区块链技术提出了医疗数据管理系统MeDShare.在该系统内，对数据的操作行为都将以防篡改的方式记录下来，并且通过访问控制机制进行用户权限的管理.但是其访问控制通过访问控制表实现，验证用户权限时开销比较大.文献[11]基于联盟链并使用可搜索加密技术[12]和秘密分享技术[13]，设计了一个基于区块链的医疗数据共享方案.在该方案中，希望得到共享数据的多个用户将获得搜索凭证的密钥份额，并提供给联盟链进行验证，验证通过后会得到搜索凭证，进而向数据服务器请求相应的密文，密文会被提交给智能合约进行解密，从而得到数据明文.此方案考虑到了云存储服务器并非完全可信的问题，并使用秘密分享技术来支持多个用户的共享，但该方案的交互过程相对复杂，联盟链、云服务器、数据拥有方和请求方之间都有交互，系统耦合性比较高.

随着使用区块链进行访问控制的相关研究不断深入，学者们开始注意到数据共享过程中的监管问题.文献[14]使用代理重加密技术[15]进行数据共享，同时保证数据拥有方对数据有一定程度的可控性.当用户有下载文件的权限时，第三方代理就会将数据密文和密钥的重加密密文发给用户，用户用自己的私钥解密出密钥，从而获得数据明文.该方案使用区块链对用户权限进行验证，并且记录请求内容，实现一定程度的监管性.文献[16]从时间维度的访问控制出发，结合属性基加密[17]和区块链，设计了医疗数据的共享方案.数据拥有方在给其他用户授权时，会部署一个限时智能合约，只有用户同时满足访问控制结构和时间范围才能获得数据.该方案虽然设置了监管中心对用户的身份进行管理，但是监管中心无法监管共享请求，也不知道是否有非法共享行为发生.另外，从时间维度对数据共享进行限制的灵活性不高，只要用户符合访问控制结构，那么在相应的时间段内用户可以随意获得数据，拥有方无法撤回授权.

从上述分析中可知，敏感数据共享过程仍存在待解决的问题：1)数据拥有方无法灵活地进行权限更新和撤销.2)数据共享本身缺乏监管性，有方案确实设置了监管中心，但监管性比较弱.鉴于敏感数据的重要性，必须有一个强监管方来保证数据共享过程的合法合规.3)共享过程中的用户身份隐私问题也需要考虑，共享本身是双方之间的交互过程，不相关的第三方不能获取到参与方的身份信息.针对这3个问题，本文以区块链技术为背景，提出了一个可控、可追责的敏感数据共享方案，旨在提高数据共享的隐私性、可控性和可监管性.该方案可以确保数据拥有方对数据的控制权，设置监管方以监督共享全过程，避免非法行为的出现.并且数据共享的行为将记录在区块链上，利用区块链不可篡改等特性，监管方可以追溯数据的使用过程，在非法行为出现时找到相关参与方进行问责.引入强指定验证者签名技术，保护了数据请求方的身份隐私.在访问控制方面使用动态累加器，使得数据拥有方可以灵活地对授权用户进行管理，包括权限的更新和撤销等，增强了拥有方对自己数据的可控程度.

2 相关假设

2.1 强RSA假设

设n=pq为RSA模，c∈强RSA假设是指在不知道n的分解的前提下，计算a,b∈使得ab=cmodn是困难的.

2.2 离散对数(discrete logarithm, DL)假设

2.3 计算性Diffie-Hellman(computational Diffie-Hellman, CDH)假设

给定生成元为g的q阶循环群，对于x,y∈R已知(g,gx,gy)，CDH假设是指对于任何运行在多项式时间t内的算法A，正确计算gxy的概率是可以忽略的.

2.4 判定性Diffie-Hellman(decisional Diffie-Hellman, DDH)假设[18]

给定生成元为g的q阶循环群，对于x,y,z∈R已知(g,gx,gy,gz)，DDH假设是指对于任何运行在多项式时间t内的算法A，正确判断是否有z=xymodq成立的概率是可以忽略的.

2.5 间隙性Diffie-Hellman(gap Diffie-Hellman, GDH)假设[19]

给定生成元为g的q阶循环群，对于x,y∈R已知(g,gx,gy)，GDH假设是指借助于DDH预言机的前提下，对于任何运行在多项式时间t内的算法A，正确计算gxy的概率是可以忽略的.

3 方案定义

本文方案包含的算法有10个：

1)Setup(1k)→params为系统初始化算法.以安全性参数1k为输入，输出公共参数params.

2)KeyGen(params)→(skA,pkA,skB,pkB,skR,pkR)为密钥生成算法.输入公共参数params，输出数据拥有方密钥对(skA,pkA)、数据请求方密钥对(skB,pkB)和监管方密钥对(skR,pkR).

3)AccInit(params)→(Acc,C)为累加器初始化算法，由数据拥有方执行.为属于自己的数据设置一个访问控制结构，输出累加器Acc和授权集合C.

4)ShareRequest(params,skB,pkB,pkA)→reqShare为共享请求算法，由数据请求方执行.输入公共参数params、数据请求方的密钥对(skB,pkB)和数据拥有方的公钥pkA，输出共享请求reqShare.

5)Authorization(params,skA,reqShare,Acc,C)→(0|witnessB,witness)为授权算法，由数据拥有方执行.输入公共参数params、数据拥有方的私钥skA、共享请求reqShare、当前累加器Acc和授权集合C，数据拥有方根据共享请求判断是否授权，如果不授权则输出0，如果授权则输出数据请求方证据witnessB和其他授权用户的新证据witness.

6)RegulateRequest(params,msg,pkA,skB,pkB,pkR,witnessB)→reqRegulate为监管请求算法，由数据请求方执行.输入公共参数params、数据拥有方公钥pkA、请求方自己的密钥对skB，pkB、监管方公钥pkR、请求内容msg和授权凭证witnessB，请求方为监管方生成一个强指定验证者签名，并附带其他附加信息后输出reqRegulate.

7)RegulateVerify(params,pkB,skR,pkR,reqRegulate)→(0|σR)为监管验证算法，由监管方执行.输入公共参数params、请求方公钥pkB、监管请求和监管方密钥对skR,pkR，监管方验证信息的正确性和合法性，如果认为该请求不合法，则输出0，如果认为请求可以执行，则输出签名σR，并将请求上传到区块链中.

8)DataResponse(params,pkB,pkR,σR,wB,msg)→(0|resData)为数据响应算法，由数据服务器执行.输入公共参数params、数据请求方发来的信息pkB,σR,wB和监管方公钥pkR，数据服务器验证所有凭证是否成立，如果验证通过，则返回响应的数据，输出resData，并将响应信息上传到区块链，否则输出0.

9)Revoke(params,Acc,C)→(Accnew,witness)为权限撤销算法，由数据拥有方执行.输入公共参数params和当前累加器Acc，数据拥有方对在权限集合C中的某个用户进行权限撤销，输出新累加器Accnew和其他还存在于授权集合中的用户的证据witness.

10)RegulateSim(params,pkB,skR,pkR,reqRegulate)→σSim为副本模拟算法，由监管方在有需要时执行.为了保护数据请求方的隐私，输入公共参数params、请求方公钥pkB、监管请求reqRegulate和监管方密钥对skR,pkR，输出签名副本σSim.

4 安全模型

在本文方案中，安全性需求描述为4方面：

1) 数据拥有方可以控制自己数据的流向，即可以灵活地将数据访问权限授权给其他用户，也可以撤销对某个用户的授权；

2) 数据请求方在获得数据拥有方的授权之后，需要进一步获得监管方的授权，在与监管方通信的过程中，数据请求方的隐私得到保护；

3) 监管方可以对数据的请求、响应进行全流程的把控，一旦发现非法行为的出现，监管方将追踪到相应的共享参与方；

4) 在数据请求方与监管方交互的过程中，监管方不能破坏请求方的隐私，也不能冒充数据请求方，向数据拥有方非法请求数据.

本文假设数据服务器是可信的，且各参与方之间与数据服务器之间的信道是安全的.下面给出本文方案的安全性定义.

定义1.数据请求方匿名性.对于一个挑战者C和敌手D之间的游戏Gameanony，如果不存在任何概率多项式时间敌手能以不可忽略的优势赢得该游戏，则该方案具有数据请求方匿名性.Gameanony定义为：

1) 对于签名者S0，S1和验证者V，挑战者C为其生成密钥对——(skS0,pkS0)，(skS1,pkS1)，(skV,pkV)，并将公钥(pkS0,pkS1,pkV)发送给敌手D.

2) 敌手D在多项式时间内向下列预言机发出查询.

Osign.输入待签名消息M,pkSd(d∈{0,1}),pkV，输出对消息M的签名σ.

Osim.输入待签名消息M,pkSd(d∈{0,1}),pkV，输出对消息M的签名σ.

Over.输入待签名消息M,σ,pkSd(d∈{0,1}),pkV，当σ有效时输出1，否则输出0.

3) 敌手D输出消息M*，挑战者C抛出硬币选择一个b∈{0,1}，运行指定验证者签名算法输出σ*=Sign(skSb,pkSb,pkV,M*)，将σ*发送给敌手D.

4) 敌手D向Osign和Osim发出如步骤2)中的查询，然后输出b′，当b′=b时，敌手D赢得这个游戏.

定义2.数据拥有方可控性.如果满足以下条件，则数据拥有方可以控制自己数据的流向，即方案具备可控性：

Pr[Setup(1k)→params,KeyGen(params)→
(skA,pkA,skB,pkB,skR,pkR),
AccInit(params)→(Acc,C),
ShareRequest(params,skB,pkB,pkA)→
reqShare:Authorization(params,skA,
reqShare,Acc,C)→0]≥1-v(λ),

或者

Pr[Setup(1k)→params,KeyGen(params)→
(skA,pkA,skB,pkB,skR,pkR),
AccInit(params)→(Acc,C),
ShareRequest(params,skB,pkB,pkA)→reqShare:
Authorization(params,skA,reqShare,Acc,C)→
(witnessB,witness)]≥1-v(λ),

其中,v(λ)为可忽略函数，即数据拥有方不给数据请求方授权的概率接近于1，或数据拥有方向数据请求方授权，并为其他授权用户更新凭证的概率接近于1.

定义3.可监管性.如果满足以下条件，则监管方可以审核系统中的共享请求和响应，即方案具有可监管性：

Pr[Setup(1k)→params,KeyGen(params)→
(skA,pkA,skB,pkB,skR,pkR),
AccInit(params)→(Acc,C),
ShareRequest(params,skB,pkB,pkA)→reqShare,
Authorization(params,skA,reqShare,Acc,C)→
(witnessB,witness),RegulateRequest(params,
msg,pkA,skB,pkB,pkR,witnessB)→reqRegulate:
RegulateVerify(params,pkB,skR,
pkR,reqRegulate)→0]≥1-v(λ),

或者

Pr[Setup(1k)→params,KeyGen(params)→
(skA,pkA,skB,pkB,skR,pkR),
AccInit(params)→(Acc,C),
ShareRequest(params,skB,pkB,pkA)→
reqShare,Authorization(params,skA,
reqShare,Acc,C)→(witnessB,witness),
RegulateRequest(params,msg,
pkA,skB,pkB,pkR,witnessB)→reqRegulate:
RegulateVerify(params,pkB,skR,
pkR,reqRegulate)→σR]≥1-v(λ),

其中,v(λ)为可忽略函数，即当数据请求方的请求有问题时，监管方否定该请求的概率接近于1，或者当数据请求方的请求正确时，监管方同意该请求并生成监管凭证的概率接近于1.

5 方案构造

通过引入动态累加器方案和强指定验证者签名方案，基于区块链技术设计了一种适用于敏感数据共享的方案.在该方案中，各数据共享方拥有对自己数据的控制权，在将数据上传时就设置好访问控制结构，只有满足访问控制结构的数据请求方才有机会获得数据.监管方负责验证每一次数据的请求过程，数据的请求和响应情况将被上传到区块链中，这些记录只有监管方可以读取，并且由于区块链具有不可篡改等特性，监管方可以在出现非法行为时追溯数据的共享全过程，定位相关责任方，进而采取必要措施.

在本节中，假设有2个参与方A和B，A将数据上传到数据服务器中，B请求获得A的某些数据，共享流程如图1所示.其中，本文假设数据服务器与各参与方之间的信道是安全可信的，其余信道不可靠，需要借助如SSL/TLS等技术进行传输.本文方案约定Encpk(m)=c,Decsk(c)=m为非对称加/解密算法，Sigsk(m)=σ,Verpk(σ)=0或1为数字签名和签名验证算法，具体计算过程不再赘述.方案构造9个算法：

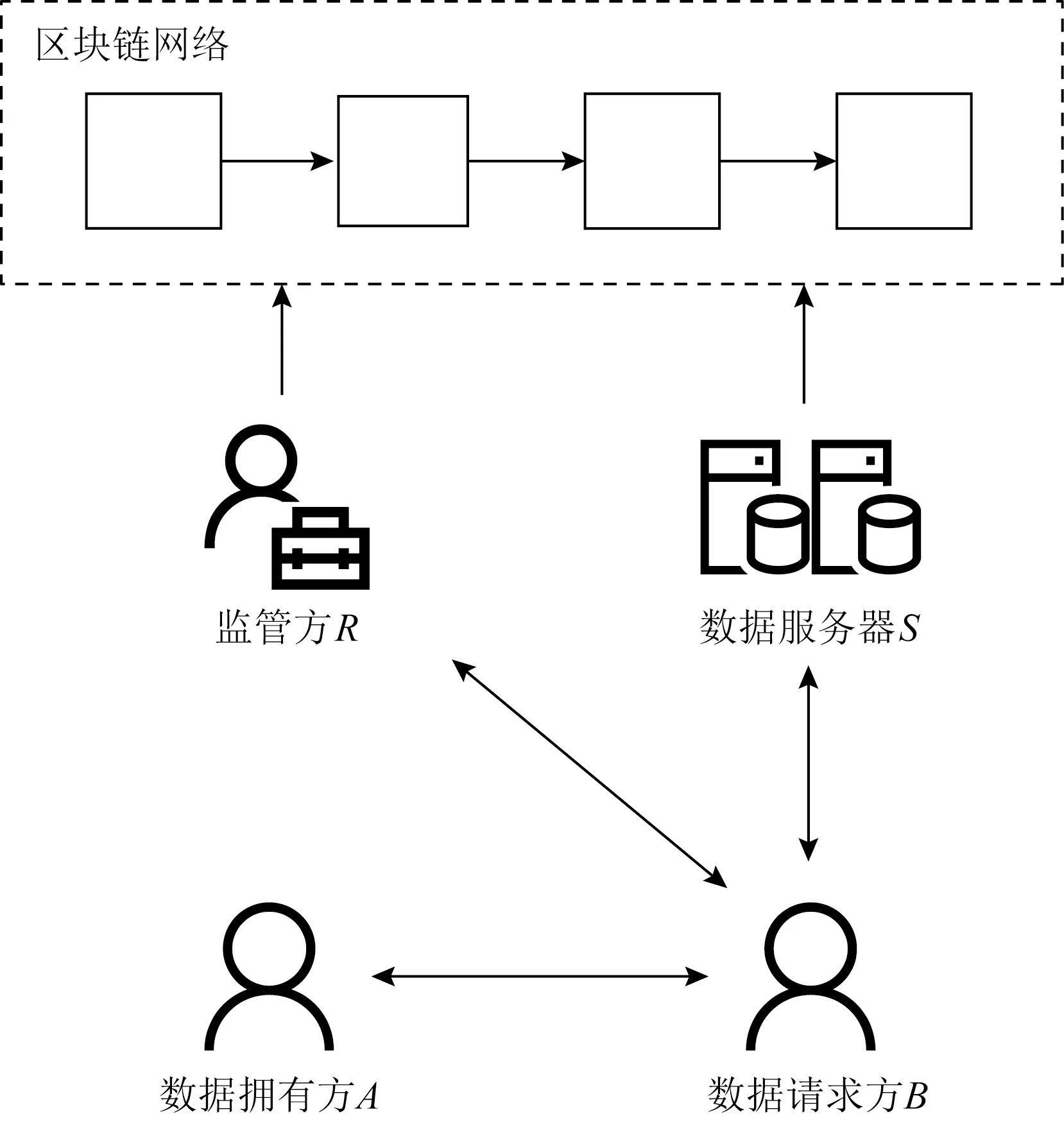
Fig. 1 Data requester B requests shared from data owner A图1 数据请求方B向数据拥有方A请求共享数据

1)Setup(1k)→params.输入安全参数1k，得到一个长度为k的随机数N，使得N=pq，其中p=2p′+1，q=2q′+1,p和q的长度相等，并且p，q，p′，q′都是素数，从N的二次剩余循环群QRN中选择一个随机数u.接着选取一个乘法群，阶为m，生成元为g，H:{0,1}×3→m为一个抗碰撞的Hash函数.输出公共参数params=(N,u,,m,g,H).

2)KeyGen(params)→(skA,pkA,skB,skR,pkR).参与数据共享的双方A和B各自生成一个随机数x1,x2∈m，令skA=x1，skB=x2，pkA=gskAmodm，pkB=gskBmodm，A的密钥对为(skA,pkA)，B的密钥对为(skB,pkB).监管方R选取随机数x∈m，监管私钥skR=x，pkR=gskRmodm，得到监管密钥对(skR,pkR).A,B,R分别保管各自的私钥，并公开公钥.

3)AccInit(params)→(Acc,C).A在本地维护一个授权集合C={c1,c2,…,cn}，其中{c1,c2,…,cn}为n个授权用户的公钥，计算累加器Acc=uc1c2…cnmodN，输出Acc.

4)ShareRequest(params,skB,pkB,pkA)→reqShare.设B想要获取的内容为msg，当前系统时间为T，计算r1=EncpkA(pkB,msg,T)，r2=SigskB(pkB,msg,T)，输出共享请求reqShare={r1,r2}发送给A.

6)RegulateRequest(params,msg,pkA,skB,pkB,pkR,witnessB)→reqRegulate.B收到witnessB后，计算DecskB(EncpkB(wB)),VerpkA(SigskA(wB))验证签名的正确性.若验证失败，则算法终止，回到ShareRequest；若验证成功，则生成强指定验证者签名(strong designated verifier signature, SDVS)[20].为了避免恶意监管方收到wB后，冒充数据请求方B向数据服务器S请求数据，B不能将wB直接发送给R，而是应该发送随机化后的wB，过程有4个步骤.

① 随机生成r,z,t,r′∈m；

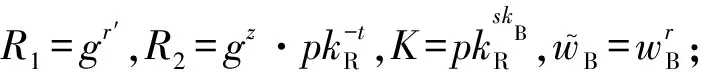
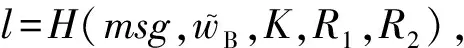
④ 输出签名σDVS=(t,z,t′,z′).

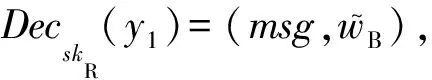
① 将σDVS解析为(t,z,t′,z′)；

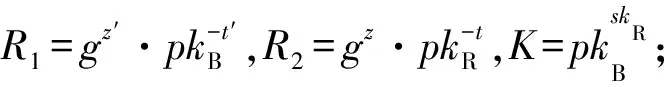
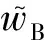
算法1.关于累加器证据的零知识证明.

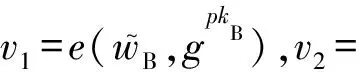
e(Acc,g);

②B生成随机数s∈m，计算

e(Acc,g)s，并将w发送给R;

③ R生成随机数η∈m，并将η发送给B;

④B计算μ=s+ηr，并将μ发给R；

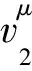
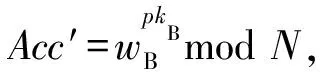
6 方案分析

6.1 安全性分析

本节分析本文方案的安全性.

定理1.如果Hash函数H为随机预言机，且GDH假设在群上成立，则该方案满足监管过程中的数据请求方隐私性.

证明.设存在一个敌手D，以(1/2+δ)的概率攻破了监管过程中数据请求方的隐私性，即攻破了强指定验证者签名SDVS的隐私性，下面使用D作为子程序，构建算法E解决GDH假设.

步骤1.E初始化GDH参数(,g,q,gu,gw)和DDH预言机，E选择一个随机数u′∈q，令pkS0=gu,pkS1=gugu′,pkV=gw，将(pkS0,pkS1,pkV)发给D，E生成初始为空的2个表格HT和ST.

步骤2.D向E进行如下查询，其中，本文假设D不进行重复查询.

1) Hash查询.输入(M,K,R1,R2)，如果E发现HT中已经存在对应的记录((M,K,R1,R2),l)，则直接返回c，否则，将(g,pkS0,pkV,K)和(g,pkS1,pkV,K)输入DDH预言机，分别得到b0和b1.如果b0=1，则输出K并中断；如果b1=1，则输出K/(gw)u′并中断.如果b0=b1=0，则生成随机数τ∈q，将τ返回给D并在HT中增加((M,K,R1,R2),l).

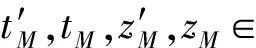
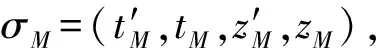
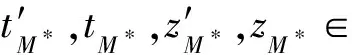
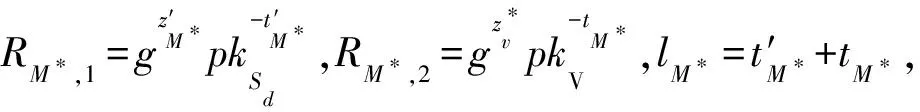
步骤4.D输出b′作为对b的猜测.

在步骤2中，D要想在验证查询阶段得到返回值为1，则需要其输入的签名σM*合法，而合法的签名将通过Hash查询获得，但D有可能不通过Hash查询而猜出一个合法的签名，这种情况的概率为1/q.因此，通过Hash查询获得合法签名的概率最小为(1-1/q).而D赢得Gameanony的概率为(1/2+δ)，但是D有可能没有通过Hash查询，只是随机选择lM*使其赢得Gameanony，这种情况的概率为(1/2+1/q)，因此D经过上述步骤得到正确结果的概率为((1/2+δ)-(1/2+1/q))，所以E解决GDH问题的概率为：

由上式，εGDH不可忽略，与GDH假设矛盾.

证毕.

定理2.在数据共享过程中，只有持有数据拥有方凭证的其他参与方，才有可能获得数据，即数据拥有方具备数据的可控性.

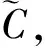
证毕.

定理3.对于系统中的所有数据共享请求，监管方能够审核共享请求与响应，即方案具有可监管性.

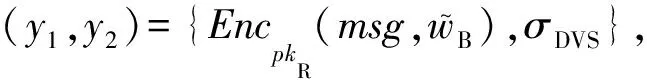
证毕.

定理4.监管方权力限制.监管方无法破坏数据请求方隐私性，也不能冒充获得授权的数据请求方非法获得数据.

证明. 在本文方案中，数据请求方将用SDVS来请求监管方的审核，由于该SDVS方案具有非授权性和非传递性的特征，因此没有第三方可以验证或者生成合法的签名.除此之外，在监管方验证授权凭证时，通过交互式证明协议，在不泄露凭证本身的前提下证明了正确性，因此监管方无法冒充合法的被授权方去获取数据.

证毕.

定理5.监管方可以通过对区块链上存储的信息进行读取，获取到某个敏感数据共享过程的相关信息，在发现问题时进行追责.

证明.在本文方案中，数据服务器S在返回给数据请求方数据时，需要构建resData=(msg′,pkB,T′)，并计算EncpkR(resData)上传至区块链中.resData包含数据共享过程的参与方、共享内容等信息，监管方R可以解密这些信息从而进行追责.

证毕.

6.2 比较分析

将本文方案与文献[4,9,11,14]中的方案进行安全性对比，如表1所示：

Table 1 Comparison of Security表1 安全性对比

由表1可以看到，本文方案对比其他方案，在实现敏感数据可控的前提下还具有一定程度的隐私性，对于共享过程，监管方可以进行监管，同时监管方的权力将受到限制.

文献[10]同样使用访问控制技术进行权限的更新与撤销，将本文方案与文献[10]中的方案进行复杂度的对比，结果如表2所示：

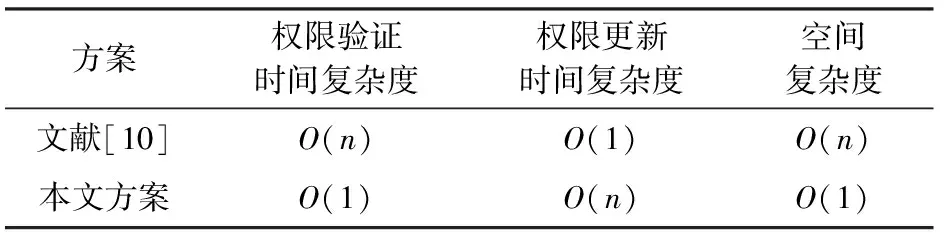
Table 2 Comparison of Complexity表2 复杂度对比

由于文献[10]中通过访问控制表进行访问控制，当需要验证用户权限时，需要遍历整个访问控制表，所以其时间复杂度为O(n)，且需要存储整张表，空间复杂度为O(n).而本文方案中使用累加器进行访问控制，只需要用户自己的凭证，结合公开的累加器即可验证，其时间复杂度为O(1)，并且验证方只需要累加器本身即可进行验证，无需额外存储信息，空间复杂度为O(1).所以本文方案的访问控制结构比较高效.并且本文方案相比文献[10]，在做到高效访问控制的同时，还实现了一定的隐私性和追责性.

文献[21]使用代理重加密和可搜索加密技术进行医疗数据共享，其数据共享阶段包括陷门生成、搜索、解密3个阶段.表3展示了常用密码学计算步骤的计算成本，将本文方案与文献[21]进行比较，2个方案的计算成本如表4所示.

Table 3 Computational Cost of Common Cryptographic Algorithms

Table 4 Computational Cost of Schemes表4 方案计算成本

综合表3和表4可得，本文方案在数据加密阶段的计算成本明显低于文献[21].在数据共享阶段，文献[21]的计算成本约为29.209 8ms，本文方案的计算成本约为32.761 3ms，计算成本增加了约12%，这主要是因为本文方案在数据共享阶段设置监管方对数据共享过程进行监管，提高了方案的安全性，所以计算成本有所增加，但在可接受的范围内.

在方案仿真部分，本实验使用Java语言，调用java.math.BigInteger库与第三方jpbc库，针对本文方案中的各种算法进行了仿真.实验环境配置如表5所示：

Table 5 Experimental Environment Configuration表5 实验环境配置

实验分别设置安全参数长度为512 b和1 024 b，记录每个算法的运行时间，为了保证实验数据的可靠性，每一个算法的运行时间均多次重复运行后取平均值，不同安全参数下各算法的运行时间如表6所示.

从表6中可以看出，在安全性参数长度为512 b时，Setup算法和AccInit算法由于需要生成一系列的参数所以耗时比较大，但是这2个算法往往只在系统启动时执行一次，所以不会对系统整体效率产生影响.其余算法运行时间均为毫秒级别，效率比较高.当提高安全性参数时，只有Setup和AccInit两个算法受到比较大的影响，其余算法均比较稳定.综上，本文方案在保证了较高安全性的同时，还具有良好的运行效率.