超声导波对含螺纹连接结构管道损伤检测研究

黄永跃 方明月 王月朋 张艺越

（安徽信息工程学院机械工程学院 安徽芜湖 241000）

管道广泛存在于工业厂房及城乡建设中，用以输送油、水及燃气等各类介质，而由管道损坏产生的经济及安全问题也不容忽视，因此需要定期对管道进行检测[1]。无损检测正是智慧工业制造的一个关键环节和质量保障，其中超声导波检测技术以其单点长距离检测的优势在管道无损检测领域的应用日益广泛，与传统的超声检测相比极大提高了检测效率[2-3]。M.V.Brook等[4]利用L(0,2)模态超声导波对管道进行缺陷检测，其施加的导波信号为垂直于管道端面的位移载荷，结果表明L(0,2)模态超声导波可以实现管道损伤的准确定位检测。Lowe等[5]利用L(0,2)模态超声导波实现了对单层管道缺陷的检测分析，获得了相应的缺陷反射系数曲线。Wang X等[6]采用数值模拟的方式分析管道中环状缺陷边缘对反射信号的影响，得出了缺陷边缘检测信号分布规律。Armenakas等[7]对管道中超声导波传播的多模态性和频散特性进行了分析，总结了超声导波在空心管道中的一般传播特性。李阳等[8]使用有限元数值仿真方法分析了超声导波在弯曲管道中的传播规律及特性，并搭建实验平台对影响导波在管道中传播的因素进行了细致分析。陈仕林等[9]以真空管道作为检测对象,分析了超声导波对其检测的有效性，并对一系列关键问题进行了探究。高望等[10]利用超声导波对火炮身管中的多种类型的环状损伤进行了有效检测，解决了复杂缺陷的识别问题。石崴巍等[11]利用数值模拟分析了含聚乙烯包覆层管道中超声导波的衰减特性。周琛等[12]基于L(0,2)模态超声导波对焊接弯管及其存在的相关缺陷进行了分析，提出了评估管道损伤程度的一般方程，并且开展相关实验验证了数值模拟的准确性。

由以上分析可以发现，国内外相关学者和工程技术人员对超声导波管道检测的研究对象多集中于光滑直管道、无缝钢制弯管及焊接管道等，而长距离管道及弯曲管道的转弯处常存在转换接头，其中螺纹连接是最常用的连接方式之一，此时超声导波的传播及对损伤的识别效果势必会受到相应的影响，分析含螺纹结构的金属管道中超声导波传播特性及损伤检测技术对实际工程应用具有一定的参考价值。

一、超声导波检测基本理论

（一）检测原理。超声导波属于机械振动的一种微观表现形式，其可在板状物体、柱体及圆管等有明确有限边界的介质（又称波导）中持续传播。导波的传播即是质点在弹性波导中振动信号的传递，若在管道的某一端面以合适的方式（采用压电传感器、磁致伸缩传感器等）对其施加位移载荷，则与传感器相接触的质点即产生高频振动，进而带动相邻质点一起振动，由此在管道中形成可按一定方向传播的超声导波，对于阻力较小的介质，超声导波的一次有效传播距离可以达到百米以上。当超声导波沿管道轴向进行传播时，如遇到裂纹、腐蚀减薄区域等损伤以及焊缝或端面等不连续界面时，将会发生导波的反射和衍射等现象，通过检测传感器接收上述信号，即可实现损伤或断面等特征的定位与识别，此即为超声导波用于管道无损检测的基本原理，如图1所示。

图1 超声导波管道检测基本原理示意图

（二）导波的多模态与频散特性。超声导波通常可以按照质点振动方式和传播路径分为三类，即：纵向模态L(0,m)、扭转模态T(0,m)和弯曲模态F(n,m)，其中n表示周向阶数，m表示模数。纵向模态导波的质点振动方向和导波的传播方向保持一致，均为轴向；扭转模态导波的质点沿周向振动，而其传播方向为轴向，此时二者相互垂直；而对于弯曲模态超声导波，其质点不存在固定的振动方向，传播特性也较不可控，因此在实际工程检测中应用较少。

与体波等常规超声波不同，超声导波存在着其自身独有的频散特性和多模态性。频散现象[13]是指对于不同频率下的超声导波，其相速度和群速度一般均不相同。相速度是指某固定频率下导波的传播速度，即波包上固定某一点的速度；而群速度则表示波包能量的整体传播速度，即波包上具有某种特定的特征的点的传播速度，通常取波包上振幅最大处的速度为该波包的群速度。在进行管道超声导波检测时，一般采用群速度来区分其模态。通过计算导波振动方程，可绘制出常见的外径60.3mm，壁厚3.5mm的20#钢管的群速度与相速度频散曲线，如图2所示。

图2 管道中导波的频散曲线

由图2可知，同一频率下存在着多种模态的超声导波，且不同频率下同一模态超声导波的相速度及群速度一般也不同。在0～300kHz内，扭转模态导波仅有T(0,1)模态存在，且其相速度和群速度始终保持不变，由此可知T(0,1)模态导波是非频散的；纵向模态导波同时存在L(0,1)和L(0,2)模态，其中L(0,2)模态导波的群速度大于L(0,1)模态，L(0,2)模态超声导波的能量也更大，二者的群速度和相速度均远超T(0,1)模态导波。由于L(0,2)模态导波群速度较大且能量集中的优势，因此检测效率较高，并且当频率超过一定的数值时（通常为50kHz），几乎也不发生频散现象，因而在工程中得到广泛应用，本研究亦采取L(0,2)模态超声导波。

（三）超声导波的运动解析。导波运动解析方程[14]是有限元数值模拟的理论依据，在进行数学模型分析时，管道一般被视作空心圆柱体。

图3中，a表示空心圆柱体内径，b表示其外径，不考虑外界条件的影响时，其外壁的边界条件为：

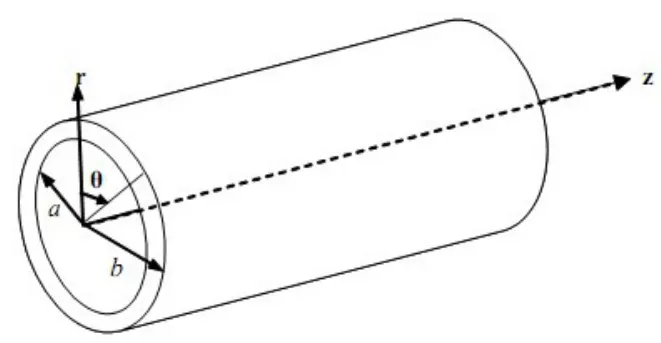
图3 柱坐标系中的管道模型

其一般的弹性运动学方程（即Navier控制方程）为：

其中，λ和μ为拉梅常数，u表示时间谐振位移矢量，ρ为材料密度。

超声导波沿空心圆柱管道传播的时域简谐解可表示为：

其位移分量为：

其中，u表示位移矢量，ur表示径向分量，uθ表示周向分量，uz表示轴向分量，Ur、Uθ、Uz表示由贝塞尔函数构成的位移幅值，n表示周向阶数，ω表示角频率，k表示波数。

二、有限元数值模型与实验验证

（一）空管道数值模型。在有限元软件中建立了一根外径为60.3mm，壁厚为3.5mm的DN50系列标准管道，其总长度为800mm，三维模型如图4所示。所用材料为20#钢，其密度为7850kg/m3，弹性模量为211GPa，泊松比为0.286。

图4 空管道三维模型

本数值模拟选用固体力学物理场进行瞬态分析，信号激励和接收采用自发自收式，在管道的左端面沿轴向加载汉宁窗调制的正弦信号作为位移载荷输入，信号中心频率为70kHz，周期数为6，其函数表达式和时域波形图分别如式（5）和图5所示。

图5 激励信号时域波形

其中，f表示中心频率，单位为Hz；t表示时间，单位为s。

通过提取不同时刻下的波场云图，得到相应结果，如图6所示。

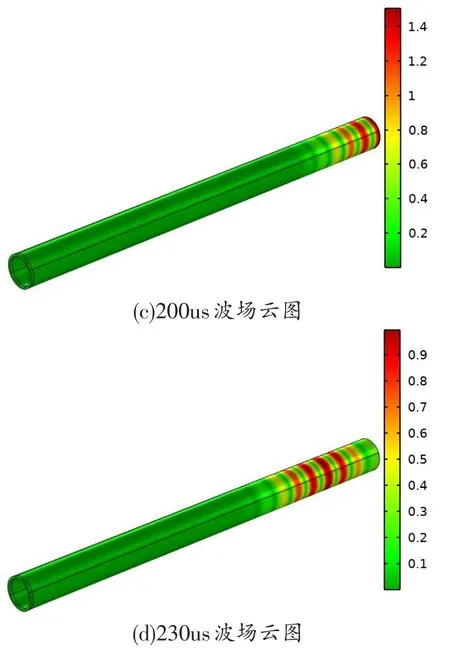
图6 不同时刻下超声导波波场云图

由上图可知，在空管道条件下，入射超声导波的振动图呈对称模式，且在管道中平稳运动，当导波到达右端面时会产生反射回波，在距离信号激励端5mm处的平面上设置信号接收面探针，得到的时域信号如图7所示：

图7 时域信号

导波群速度计算公式为：

式中，vg表示导波波包群速度，Δl表示导波波包传播的路程，Δt表示导波波包传播的时间间隔。

由图可知入射波的峰值对应的时刻为50us，接收到的端面反射回波的时刻为351us，代入上式可得：

该数值符合L(0,2)模态超声导波的群速度标准，因此该有限元模型是符合理论要求的。

（二）实验验证。利用磁致伸缩超声导波检测仪搭建了管道检测平台，该平台包括主机、检测传感器、待测管道等三部分，由仪器主机控制检测传感器发出脉冲激励信号，实现超声导波的激励和接收。管道有效长度为800mm，材料参数与有限元模型保持一致，该实验平台如图8所示：

图8 超声导波管道检测实验平台

通过该实验平台检测得到的时域信号如图9所示，图中出现两处波包，第一处为始脉冲波，其中包含电磁干扰波，因此使得靠近传感器的区域出现检测盲区；第二处波包为管道端面回波，端面回波位置和有限元数值模拟结果基本一致。综上，所建立的有限元数值模型符合理论数据和实验结果，从而进一步证明了有限元数值模型的正确性，后文可利用本节建立的模型进行有效模拟。

图9 实验信号

三、含螺纹结构管道的损伤检测分析

（一）管道建模与参数设定。基于上述第二部分建立的数值模型，在管道轴向正中间添加了55°标准管螺纹，以此模拟管道螺纹接头的内部结构，其参数如表1所示。

表1 管螺纹参数

为测试超声导波对螺纹结构后方管道损伤的检测效果，在距离管道左端面600mm处预置了一处环状损伤，沿轴向的宽度为2mm，管道模型示意图如图10所示。

图10 管道模型示意图

在管道左端面沿管道轴向施加式（5）所示的位移载荷信号，分别提取了不同时刻下超声导波的波场云图，如图11所示。

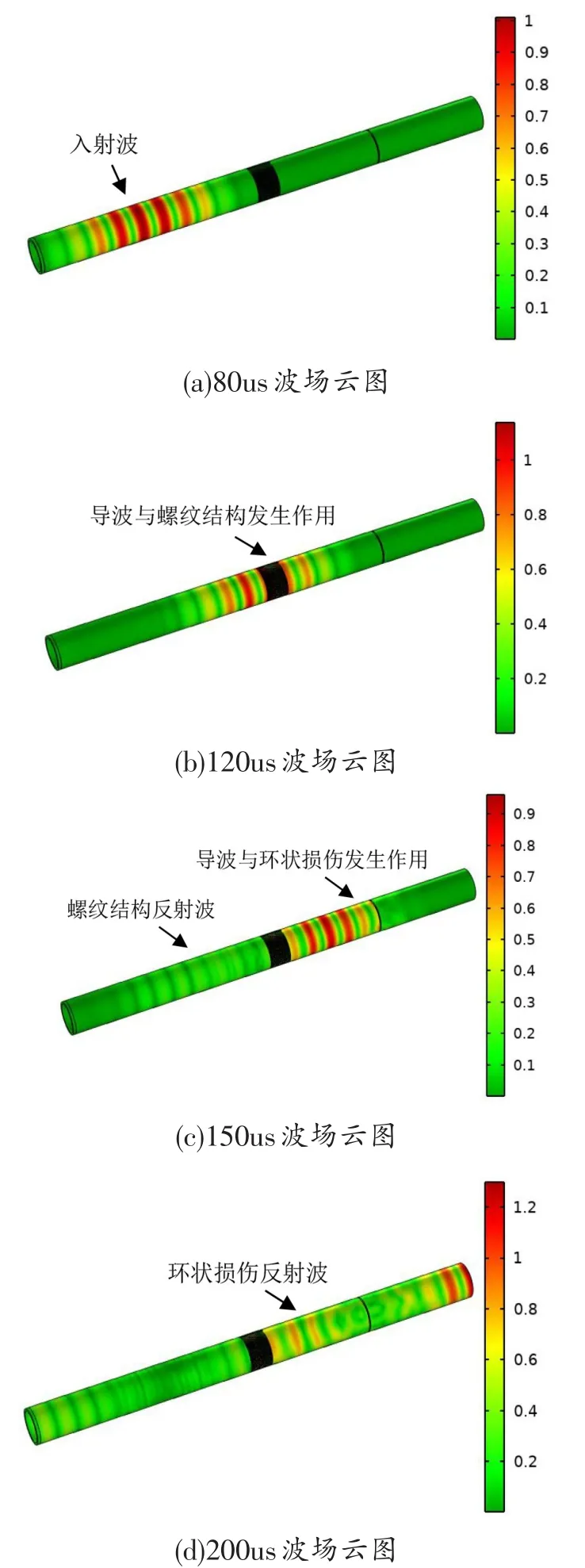
图11 不同时刻下管道中超声导波的波场云图

由图11可知，导波遇到螺纹结构和环状损伤时均会发生明显的反射现象，因此螺纹结构的存在将会对环状损伤的检测产生一定的干扰，为探究螺纹结构的存在对损伤检测灵敏度的影响，对环状损伤的规格大小做出了系列调整。

（二）环状损伤的周向长度对检测结果的影响。将环状损伤设置为通透型，即损伤的厚度与管道壁厚相同，分别研究环状损伤周向长度为L/8、L/4、3L/8、L/2、5L/8以及3L/4（其中L为管身周长）等6种条件下的时域检测信号，其时域信号分别如图12所示：

图12 不同周向长度下的时域检测信号

由检测信号图可知，对于不同周向长度的通透型环状损伤，在螺纹结构的影响下，其仍然能够被超声导波检测出来，但幅值大小各有不同，如图13所示，当损伤长度为L/8时，其信号幅值为0.093mm，小于螺纹结构的信号幅值0.170mm；随着损伤长度的增加，损伤检测信号的幅值逐渐升高，而螺纹结构信号幅值始终保持0.170mm不变；当损伤长度为L/4时，损伤检测信号的幅值为0.180mm，已超过螺纹结构的信号幅值。

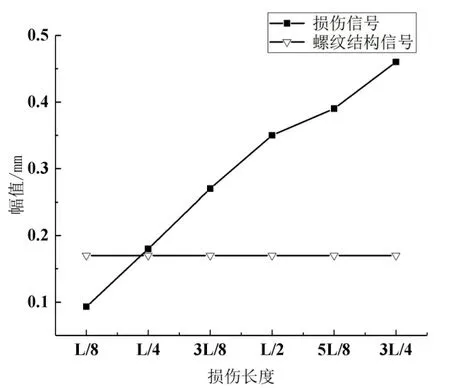
图13 不同损伤长度信号幅值变化图

在定位准确性方面，当损伤周向长度为L/8时，入射波对应的波包峰值为50us，损伤波对应的波包峰值为272.5us，由前述计算所得L(0,2)模态导波的群速度为5300m/s，可算得该损伤与管道左端面的距离为：

与实际损伤的相对误差为：

同理，可计算得其余5种情况下的相对误差均为1.3%，定位准确性较高。

（三）环状损伤的厚度对检测结果的影响。保持环状损伤的周向长度一致，均为L/2，分别研究损伤厚度为H/5、2H/5、3H/5以及4H/5（其中H为管道壁厚）等4种条件下的时域检测信号，其时域信号如图14所示：

图14 不同损伤厚度下时域检测信号

由检测信号图可知，随着损伤厚度的增加，损伤检测信号的幅值在逐渐升高；针对不同厚度的环状损伤，在螺纹结构的影响下，对于厚度为H/5的损伤，其时域信号幅值远远小于螺纹结构信号，超声导波无法对其进行有效检测；在损伤厚度达到2H/5和3H/5时，虽然其时域信号幅值仍小于螺纹结构信号，但已经能够明显分辨出来；当损伤厚度达到4H/5时，其信号幅值已超过螺纹结构的反射信号。

图15 不同损伤厚度信号幅值变化图

对于定位准确性，按照前述计算方式，可算得定位相对误差无变化，仍为1.3%。由此可见，损伤的厚度仅对信号幅值影响较大，而对其定位准确性并无明显影响。

四、结论

（一）通过有限元建模，采用对管道施加轴向位移载荷的方式激励出了L(0,2)模态超声导波，获得了其实际波速，并通过磁致伸缩超声导波检测仪搭建管道检测实验平台，验证了有限元模型的正确性；

（二）对于不同周向长度的通透型环状损伤，在螺纹结构的影响下，其仍然能够被超声导波检测出来，且定位准确性较高，其相对误差均为1.3%；随着损伤长度的增加，损伤检测信号的幅值逐渐升高，而螺纹结构回波信号幅值始终保持为0.170mm；当损伤长度为L/4时，损伤检测信号的幅值已超过螺纹结构的信号；

（三）对于同一周向长度但厚度不同的损伤，随着厚度的增加，损伤检测信号的幅值在逐渐升高；对于厚度为H/5的损伤，其时域信号幅值远远小于螺纹结构信号，因而超声导波无法对其进行有效识别；当损伤厚度达到2H/5和3H/5时，其时域信号幅值仍小于螺纹结构信号，但已能够明显辨别，定位相对误差为1.3%；当损伤厚度达到4H/5时，其信号幅值超过螺纹结构的反射信号。