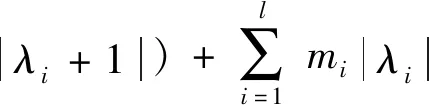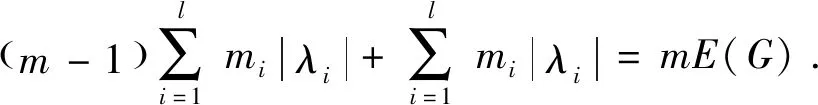若干等能量图族的构造①

王洪波

(集美大学理学院，福建 厦门 361021)

0 引 言

设G是一个顶点集为V={v1,v2,…,vn}，边集为E的简单图.图G的邻接矩阵定义为A(G)=(aij)n×n，其中aij=1，若vi与vj相邻；否则aij=0.A(G)的特征多项式被称为G的特征多项式，记为ψ(G,λ)=det(λI-A(G))，其根也被称为G的特征值.由于A(G)是实对称的，故其特征值是实数[1].记G的全部互异特征值为λ1,λ2,…,λl，这些特征值的代数重数分别为m1,m2,…,ml，其中m1+m2+…+ml=n.G的全部互异特征值连同它们的重数被称为G的谱，记为

图的特征值的绝对值之和被定义为图的能量.能量是一类重要的图指标，与共轭碳氢分子的π-电子能量紧密关联.若两个图的能量相同，则称这两个图是等能量的.与能量有关的问题被许多学者研究[2-3]，许多的文献都给出了构造等能量图的方法.Ramane等[4-5]利用线图的性质给出两个非同谱等能量无限图族；Kwong等[7]利用删边运算给出许多对等能量图(图对中一个图是另外一个图的子图)；Saroja等[6]给出了一些由完全图构造而成的正则等能量图；王洪波等[8]利用联并图的谱的性质给出一个构造等能量图的方法.本文利用矩阵的相关性质构造了若干等能量图族.

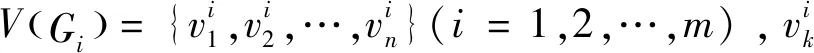
例如，若G=P3(长度为2的路)，m=4，则G(1),G(2),G(3),G(4),G(5)分别如图1所示.

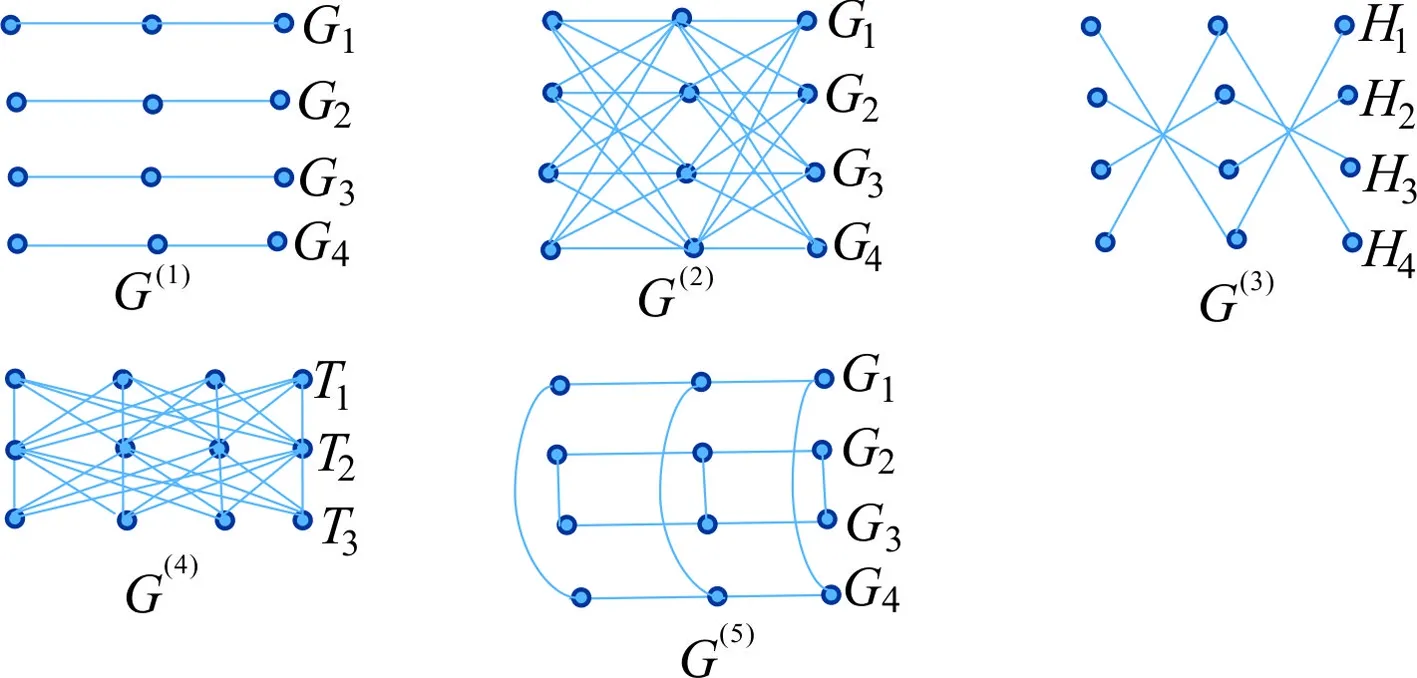
图1

1 相关引理

若矩阵A=(aij)m×n，B=(bij)p×q.定义A和B的Kronecker积为

引理1[1]设A=(aij)n×n的特征值为λ1,λ2,…,λn，B=(bij)m×m的特征值为μ1,μ2,…,μm，则A⊗B的特征值为{λiμj|1≤i≤n,1≤j≤m}.

引理2 设A,B,C,D是n阶方阵，则

证明：记左边的行列式为D2nm，由Laplacian展开定理，将D2nm按第(m-1)n+1,(m-1)+2,…,mn,mn+1,…,(m+1)n列展开，易得

以此作递推公式，即可得

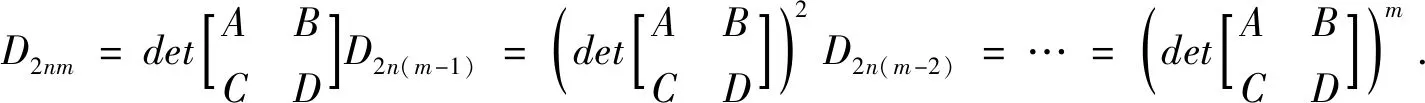
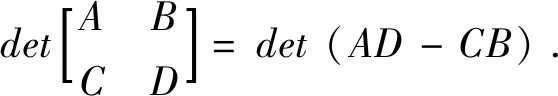
2 等能量图

定理1 设G的顶点数为n的简单图，G(1),G(2),G(3),G(4)是按前文方式构造的图.则G(1),G(2),G(3),G(4)是等能量的且E(G(1))=E(G(2))=E(G(3))=E(G(4))=mE(G).

证明：设

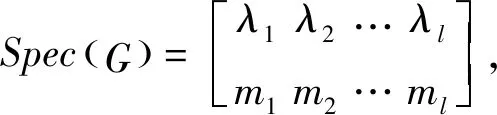
对G(1),G(2),G(3),G(4)的顶点经过适当的排序，则G(1),G(2),G(3),G(4)的邻接矩阵可以分别表示为

A(G(1))=diag(A(G),A(G),…,A(G)).

这里Jm是m阶全1方阵.

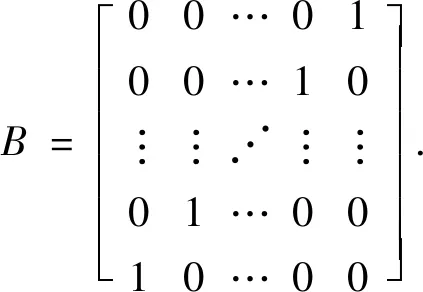
这里A(G)=(aij)n×n.

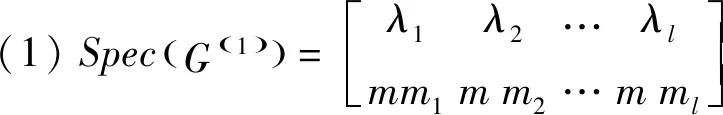
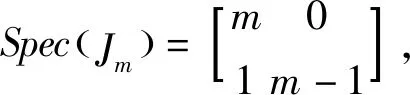
Spec(G(2))=Spec(G(4))=

从而

(3)对G(3)，分以下两种情形讨论：

Spec(G(3))=

从而

情形2若m是奇数，

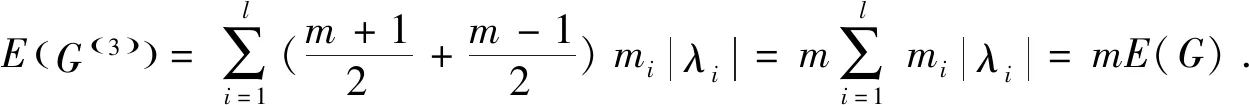
综上所述，E(G(1))=E(G(2))=E(G(3))=E(G(4))=mE(G).证毕

定理2 设G是顶点数为n的简单图且其所有特征值的绝对值都不小于1，G(1),G(2),G(3),

G(4),G(5)是按前文方式构造的图.则G(1),G(2),G(3),G(4),G(5)是等能量的且E(G(1))=E(G(2))=E(G(3))=E(G(4))=E(G(5))=mE(G).

证明：设

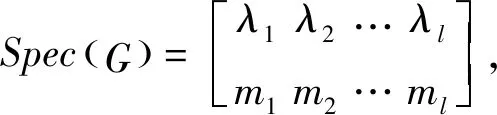
由定理1，G(1),G(2),G(3),G(4)是等能量的且E(G(1))=E(G(2))=E(G(3))=E(G(4))=mE(G).

对G(5)的顶点经过适当的排序，(1)当m是偶数时，G(5)的邻接矩阵可以表示为

从而

Spec(G(5))=

故当|λi|≥1(i=1,2,…,l)时，

(2)当m是奇数时，G(5)的邻接矩阵可以表示为

A(G(5))=

由引理2，引理3，经计算知，

ψ(G(5),λ)=

(λIn-A(G)).

从而

Spec(G(5))=

故当|λi|≥1(i=1,2,…,l)时，