正交面齿轮传动弯曲应力公式优化分析①

李晓贞, 苏 阔, 李同杰, 王 娟

(安徽科技学院机械工程学院，安徽 滁州 233100)

0 引 言

正交面齿轮作为一种新型传动齿轮，由于其具有较高的传动比，较低的振动以及噪声。正交面齿轮在国外已经成功应用于螺旋翼直升飞机传动系统、汽车差速器、农业机械传动系统中，并初步确定了的正交面齿轮设计及校核标准[1-3]。面齿轮在国内起步较晚，与上世纪八十年代引入国内，开始相关理论技术研究，目前，国内正交面齿轮还没有推广应用，主要处于理论和实验阶段，也不具完善设计及校核标准。

在正交面齿轮弯曲应力计算方面，国内外大量科研工作者对其进行了大量的研究[4-9]。北京航空航天大学的初晓孟，杨凯[10]等研究了相交轴系统面齿轮强度有限元分析，南京航空航天大学的靳光虎，周辉俊[11-13]等基于有限元法拟合了在集中载荷和均布载荷下的正交面齿轮弯曲应力，中南大学的刘艳平[14]基于ABAQUS对正交面齿轮接触应力及弯曲应力进行了分析，哈尔滨工业大学的韦贤玕[15]通过诱导法计算了正交面齿轮接触齿面的主曲率，西安科技大学徐琪超[16]通过面齿轮承载接触仿真分析获得面齿轮齿根弯曲应力以及齿面接触应力等面齿轮承载接触特性，西北工业大学付学中，方宗德[17]等对变位面齿轮进行了承载接触分析和应力场分析。

目前，对于正交面齿轮弯曲应力计算公式的拟合，主要是正交面齿轮在集中载荷和均布载荷下受力进行拟合，使正交面齿轮的受力过于极端化和理想化。没有考虑正交面齿轮实际啮合过程中的受力情况。通过建立标准安装的正交面齿轮与圆柱齿轮装配体模型，采用瞬态动力学模块对装配体模型进行有限元分析，进行正交面齿轮弯曲应力计算公式的拟合。

1 正交面齿轮齿面方程

正交面齿轮齿面是由加工面齿轮的刀具齿轮齿面，根据啮合原理和包络法推导得到。其过程建立如图1所示的包络加工坐标系。其中，OT0-XTOYT0ZTO，OT-XTYTZT为刀具齿轮固定坐标系和随动坐标系，OF0-XFOYF0ZFO，OF-XFYFZF为被加工正交面齿轮固定坐标系和随动坐标系，且随动坐标系是由固定坐标系绕Z轴转过一定角度得到的。图中φT,φF为刀具齿轮和被加工面齿轮两坐标系之间转过的角度。ωT，ωF为刀具齿轮和被加工面齿轮的转动角速度。

根据图1所示的坐标系关系与齐次坐标变换原理，从刀具齿轮的随动坐标系OT-XTYTZT到面齿轮的随动坐标系OF-XFYFZF的齐次坐标转换矩阵为

(1)

式中：T为矩阵的转置；ra为刀具齿轮的分度圆半径。

刀具齿轮轴截面形状如图2所示。图中“a-a”和“b-b”分别表示齿槽的两侧齿面。

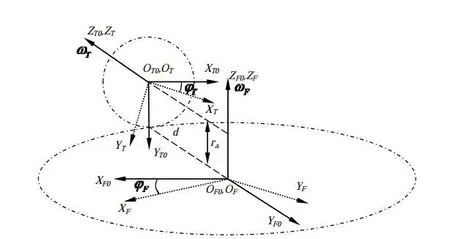
图1 正交面齿轮包络加工坐标系

根据图2得到刀具齿轮的齿面方程为

(2)

式中：αk为k点处压力角；uk为刀具齿宽方向的参变量；“+”表示右齿廓“b-b”，“-”表示左齿廓“a-a”；θk为k点处的矢径与坐标轴OTYT的夹角。

由式(1)和式(2)得到刀具齿面在面齿轮随动坐标系中的方程为

(3)

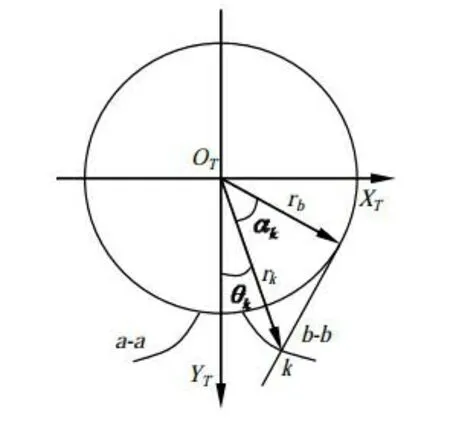
图2 刀具渐开线齿廓

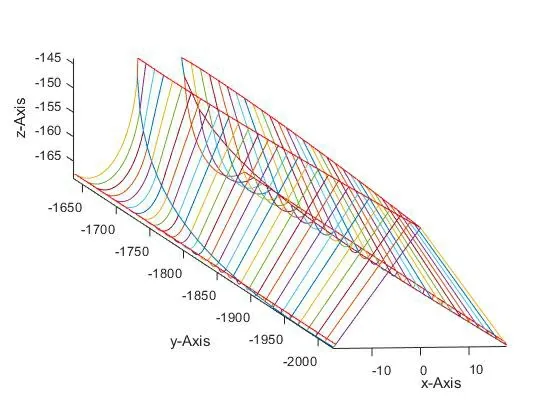
图3 正交面齿轮齿面

根据包络条件及式(3)，得到正交面齿轮齿面方程为

(4)

根据式(4)得到正交面齿轮齿面如图(3)所示。

2 正交面齿轮建模与有限元分析

2.1 试验方案

对于齿轮设计来说，可以根据不同的需求确定相应参数进行齿轮的设计，若对所有参数进行试验是难以实现的。根据正交实验方法具有高效、经济、快捷等优点，本文选取齿轮设计参数中最重要的三个参数(齿数、模数、压力角)来确定正交面齿轮，并由此确定三因素三水平的正交面齿轮弯曲应力分析模型的正交实验表，如表1。

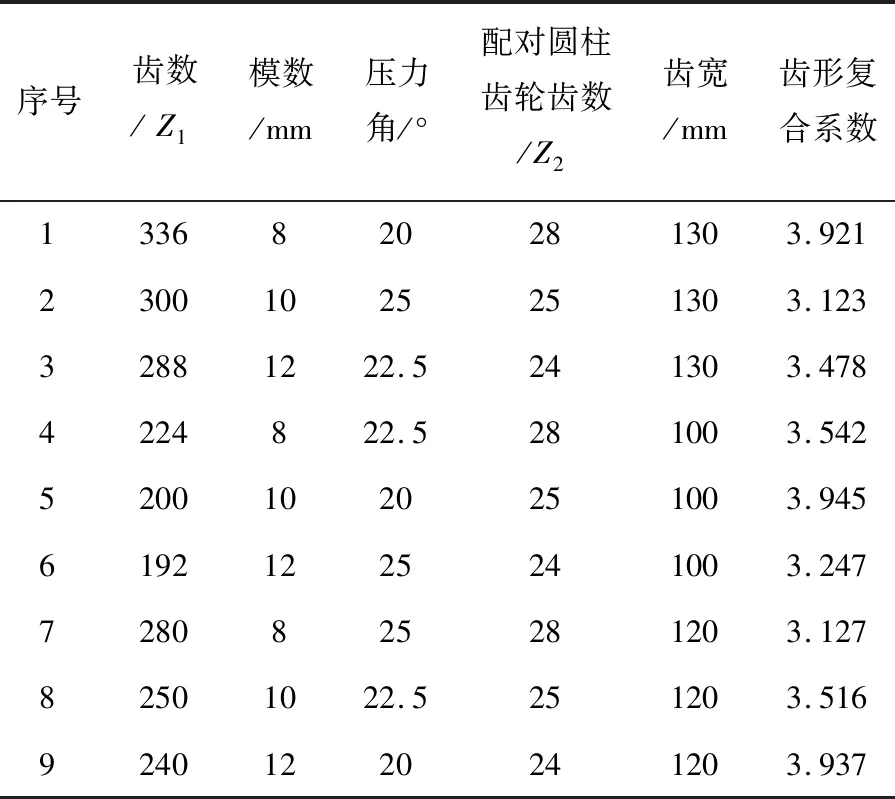
表1 正交面齿轮弯曲应力计算模型参数

根据理论计算得到的正交面齿轮与圆柱齿轮的接触半径，部分正交面齿轮接触半径如图4，使圆柱齿轮齿宽中间与正交面齿轮理论接触半径重合，且顶隙按照标准值进行装配，建立9组不同的正交面齿轮与圆柱齿轮装配体模型，部分装配体模型如图5。

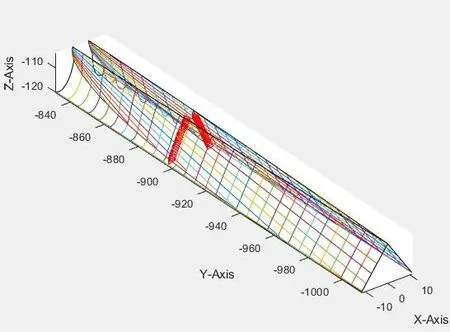
图4 齿数为224模数为8的正交面齿轮接触半径

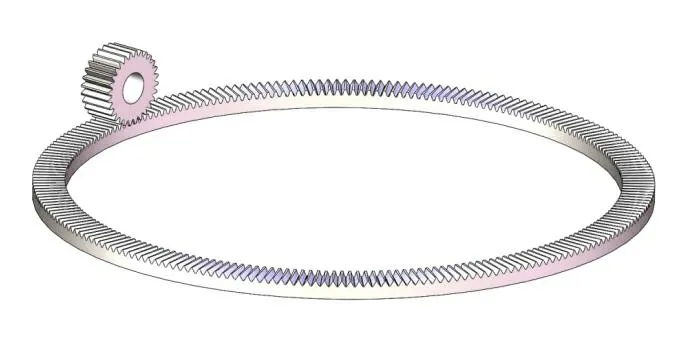
图5 齿数为224模数为8的正交面齿轮与圆柱齿轮装配体模型

由表1中的参数根据理论计算可以得到，其中最小的正交面齿轮内半径为832mm，外半径为1009mm，因此建立的9组装配体模型较大。在有限元分析时，将划分出大量的单元与节点，为了控制仿真时间，同时不影响仿真结果，将正交面齿轮与圆柱齿轮简化为两齿模型进行瞬态动力学分析，简化后的装配体模型如图6。

图6 简化后正交面齿轮与圆柱齿轮装配体模型

2.2 有限元分析

将两齿模型导入到ANSYA workbench中的瞬态动力学模块，更改材料属性为结构钢，进行六面体网格划分，同时为了使仿真结果精确，控制正交面齿轮与圆柱齿轮之间接触面的网格大小，部分网格划分如图7所示。

图7 部分装配体模型网格划分

在网格划分完成后，在正交面齿轮与圆柱齿轮齿面之间添加接触，部分接触参数表2。根据运动关系在正交面齿轮和圆柱齿轮内圆孔面上分别与大地之间添加旋转副，并在正交面齿轮与圆柱齿轮上添加相应的负载扭矩与角速度。

表2 接触参数设置

根据以上仿真设置，对建立的9组装配体模型逐一进行仿真，得到如表3所示的各组正交面齿轮负载扭矩与其对应的弯曲应力值。部分正交面齿轮应力分布云图如图8，接触区域云图如图9。

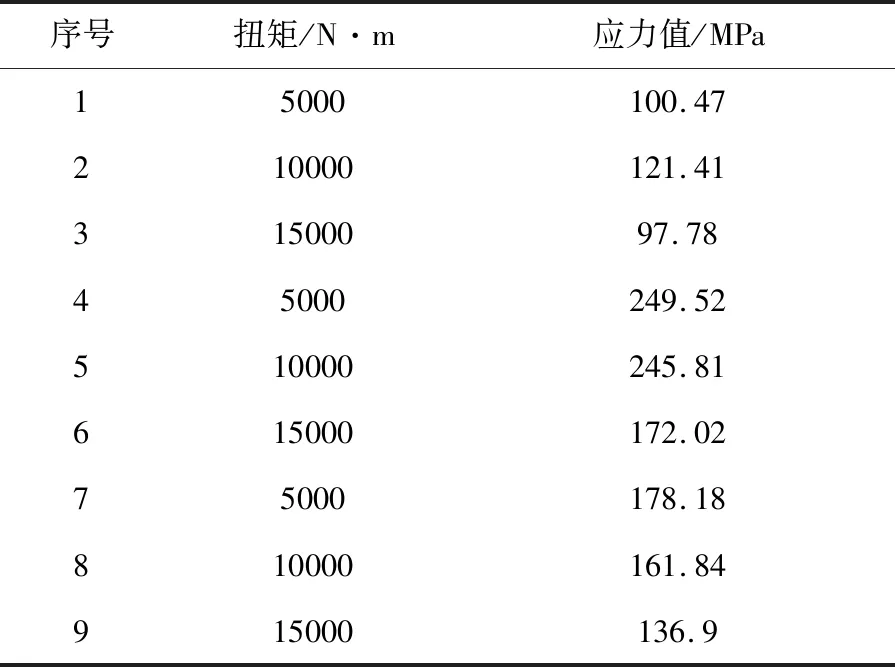
表3 9组正交面齿轮仿真分析负载扭矩与应力值

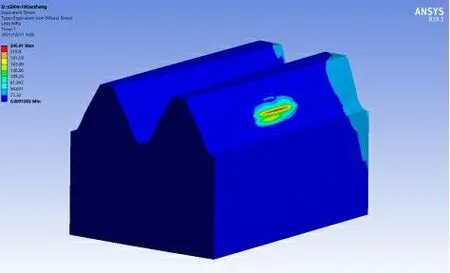
图8 部分正交面齿轮应力分布云图

图9 部分正交面齿轮接触区域分布云图

3 正交面齿轮弯曲应力计算公式拟合与分析

目前关于正交面齿轮的弯曲应力计算还没有标准的计算公式，参考已经成熟的齿轮弯曲应力计算方法以及集中载荷方式下拟合公式的推导方法如文献[11]，拟合基于标准安装传动下的正交面齿轮弯曲应力计算公式：

(5)

式中：A和B为待定拟合常数；σ0为全齿宽加载下最大弯曲应力；σ为正确啮合传动下正交面齿轮最大弯曲应力；φb=b/m；b,m分别为正交面齿轮齿宽和模数。

(6)

式中：KA为正交面齿轮工况系数；Ft为正交面齿轮所受圆周力；YS为齿形复合系数，由文献[11]中的齿形复合系数理论公式计算得到。

文献[18]中根据假设条件，简化面齿轮分析模型，拟合了基于集中载荷下的面齿轮弯曲应力计算公式

(7)

文献[12]在上述基础上通过通过改变施加载荷的位置以及拟合时采用压应力进行拟合，对正交面齿轮在受集中载荷时的弯曲应力进行优化得到式(8)，并拟合了均布载荷下的正交面齿轮弯曲应力计算公式如式(9)

(8)

(9)

根据表3中的各组正交面齿轮有限元分析值与理论计算的全齿宽条件下的正交面齿轮最大弯曲应力，获得弯曲应力比值与齿宽系数之间的关系绘制散点图，由最小二乘法对弯曲应力比与齿宽系数进行曲线拟合，得到在标准安装传动下的正交面齿轮弯曲应力比与齿宽系数拟合曲线如图10所示。

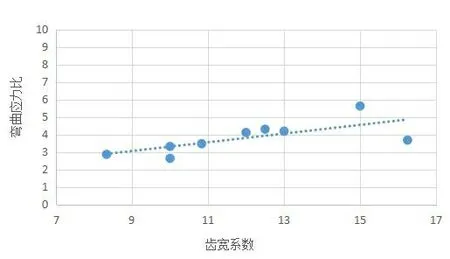
图10 正交面齿轮弯曲应力比与齿宽系数关系

根据最小二乘法拟合曲线可以看出，数据点基本分布在拟合曲线两侧，且靠近拟合曲线。得到了正交面齿轮齿根弯曲应力比值与齿宽系数近似满足一关系

(10)

则得到在标准安装传动下的正交面齿轮齿根弯曲应力为

(11)

在进行有限元分析时，是基于标准安装条件下的正交面齿轮与圆柱齿轮装配体进行瞬态动力学分析，正交面齿轮的受力方式是由其自身的负载扭矩与圆柱齿轮的驱动，通过两者之间的接触产生的，与文献[11][12]通过直接施加基于集中载荷或均布载荷下的单个正交面齿轮静应力分析不同，因此拟合公式系数存在不同，但本文所拟合的公式更适用于具体的工程案例。

根据相对误差的定义，计算基于正交面齿轮正确啮合传动下的齿根弯曲应力有限元分析值与拟合公式理论值的各组正交面齿轮相对误差对比分析表如表4，误差曲线分布如图11。

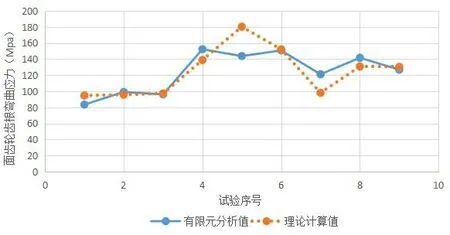
图11 标准传动下正交面齿轮齿根弯曲拟合公式计算值与有限元分析值对误差分布

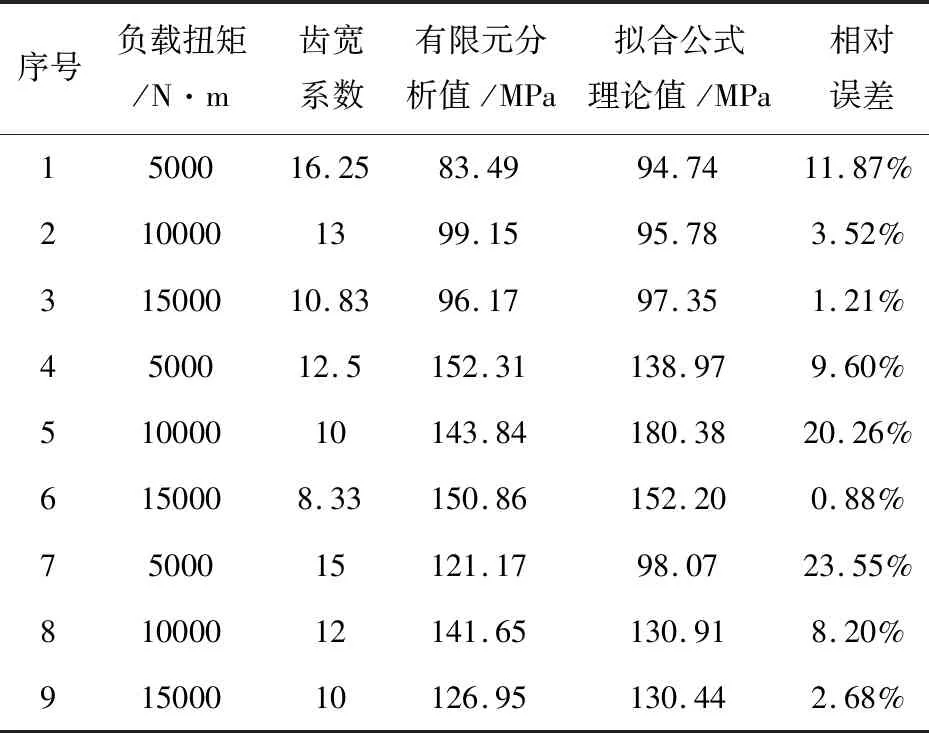
表4 9组正交面齿轮应力值分析

基于正确啮合传动下的正交面齿轮齿根弯曲应力拟合公式，得到了9组正交面齿轮弯曲应力拟合公式计算值与有限元分析值之间的相对误差。9组正交面齿轮的平均相对误差为9.08%，最小误差为0.88%，最大误差为23.55%，分别对应的齿宽系数为8.33和15。由图10可以看出，当齿宽系数在8-14之间拟合公式计算值与有限元分析值之间的误差较小，当齿宽系数大于15时，拟合公式计算值与有限元分析值之间的误差较大。

通过对比分析当正交面齿轮压力角在20°～25°之间，模数在8～12之间，且齿宽系数在8～14之间，通过有限元分析进行弯曲应力公式拟合计算的正交面齿轮弯曲应力与有限元分析所得弯曲应力之间的误差较小，在标准安装传动的条件下可以作为正交面齿轮弯曲应力的计算依据。

4 结 语

通过建立标准安装的正交面齿轮与圆柱齿轮装配体模型，使用有限元分析中瞬态动力学模块，对正交面齿轮传动过程中的弯曲应力进行分析，拟合出基于标准安装传动下的正交面齿轮弯曲应力计算公式。根据拟合公式与有限元结果进行对比分析得到两者间的平均误差为9.08%，当模数在8～12之间，压力角为20°～25°且齿宽系数在8～14之间，该计算方法可以在实际工程案例中作为正交面齿轮弯曲应力的计算方法。