带时间窗偏好的同时配集货且需求可拆分车辆路径问题

2022-12-15范厚明任晓雪

运筹与管理 2022年11期

范厚明, 任晓雪, 刘浩

(大连海事大学交通运输工程学院,辽宁大连 116026)

0 引言

带时间窗偏好的同时配集货且需求可拆分车辆路径问题(Split Delivery Vehicle Routing Problem with Simultaneous Delivery and Pick-up and Time Windows Preference, SDVRPSDPTWP)是综合考虑了同时配集货需求可拆分车辆路径问题(Split Delivery Vehicle Routing Problem with Simultaneous Delivery and Pick-up, SDVRPSDP)和带时间窗偏好的同时配集货车辆路径问题(Vehicle Routing Problem with Simultaneous Delivery and Pick-up and Time Windows Preference, VRPSDPTWP)而展开的研究。该研究涉及现实中普遍存在的物流配送问题，如：医药公司分批次配送并回收过期药物；区域物流分拣中心向各小区、高校配送快件的同时会收取寄件，由于快件数量多，且送、取件的时间要求不同，会出现多次对一个客户进行配送并收取快件的情况等。

有关SDVRPSDP的研究：Casazza等[1,2]设计了分支-定价算法求解SDVRPSDP问题。Chen等[3]设计了基于运输效率的启发式算法和变邻域搜索算法求解SDVRPSDP问题。Haddad等[4]提出了基于大邻域搜索的元启发式算法和分支-定价算法求解SDVRPSDP问题。Hennig等[5]研究了原油船的SDVRPSDP问题，设计了两种可替换的路径流模型进行求解。Hernández-Pérez等[6]设计了分支-切割算法求解SDVRPSDP问题，该问题中客户可作为临时中间点，用于货物的配送以及收集。Abdi等[7]研究的是只拆分配货需求的SDVRPSDP问题，设计了四种元启发式算法进行求解。

有关VRPSDPTW的研究：Aziez等[8]研究了带有时间窗的多收集-单配送的车辆路径问题，设计了分支-切割算法进行求解。Goeke[9]研究了电车的VRPSDPTW问题，设计了禁忌搜索算法进行求解。Györgyi等[10]研究了不确定时间窗的随机和动态配集货车辆路径问题，设计了两个启发式算法进行求解。Veenstra等[11]研究了带时间窗和装卸作业的配集货车辆路径问题，并设计了分支-定价-切割算法进行求解。Wang等[12]研究了VRPSDPTW问题，设计了并行模拟退火算法进行求解。Li等[13]设计了自适应大邻域搜索算法求解VRPSDPTW问题。

目前，关于SDVRPSDPTWP的研究成果还没有。通过文献梳理可见，以下几个方面有待更深入的研究：(1)大多求解算法在生成客户排列时仅考虑客户间的空间距离，没有考虑时间距离；(2)大多研究假设配送车辆统一固定时刻出发，而不是根据客户要求确定车辆最优出发时间；(3)部分研究设置了固定拆分阈值，分析不同拆分阈值对路径规划的影响，但拆分阈值很难合理确定。

1 SDVRPSDPTWP模型建立

1.1 参数定义

1.2 客户时间窗偏好

若车辆在客户i的规定时间窗[ETi,LTi]内到达，客户i的满意度始终为最高值1，且没有时间惩罚成本；若车辆在时间窗[EETi,ETi]和[LTi,ELTi]内到达，到达时间偏离客户规定时间窗越大，满意度越低，时间惩罚成本越大；若车辆在EETi和ELTi处到达，客户i的满意度为最低值0，时间惩罚成本为最高值；若车辆在EETi之前到达，需要等待，直到EETi才可以开始服务，客户满意度为0，时间惩罚成本为最高值；若车辆在ELTi之后到达，客户i拒绝接受服务，满意度为0，时间惩罚成本为无穷。

时间惩罚成本为车辆到达时间的隶属度函数。客户满意度和时间惩罚成本的计算公式如下:

(1)

(2)

1.3 油耗成本

车辆的油耗与车辆的载重成线性关系[14]，本文假设z1是车辆空载时的油耗率，z2是车辆满载时的油耗率，c0是单位油耗成本。若车辆k服务的客户序列为Vk={e,f,s,y},Vk∈V0，当车辆k服务完客户e,f,s后，其实时载重量Qsyk=Qefk-df+pf-ds+ps，Qefk是车辆k服务完客户e后驶向客户f的装载量，Qsyk是车辆k服务完客户s后驶向客户y的装载量。车辆k从客户s到客户y的油耗率以及油耗成本如式(3)、(4)所示:

zsyk=z1+(z2-z1)Qsyk/Q

(3)

csyk=c0zsyklsyxsyk

(4)

1.4 数学模型

基于以上所述，本文建立的模型如下:

(5)

(24)

其中，式(5)最小化总配送成本，包括派遣成本、理货成本、时间窗惩罚成本及油耗成本；式(6)表示从配送中心派出的车辆数不能多于实际拥有数量；式(7)表示车辆服务完客户点后必须离开；式(8)表示每个客户最少被服务一次；式(9)和(10)保证客户被车辆服务时一定有路径与其连接；式(11)表示车辆从配送中心被派出，完成相应服务后必须返回配送中心；式(12)表示车辆,k服务客户j前后的车辆负载平衡约束；式(13)和(14)表示每个客户的配集货需求量都得到满足；式(15)和(16)表示任一辆车对其路径上的任一客户点的配、集货量都不超过其需求量；式(17)计算车辆的服务时间；式(18)计算车辆k从客户i到达客户j的时刻；式(19)表示客户满意度最低为ω；式(20)表示两决策变量之间的关系；式(21)表示车辆k到达客户j的时间必须小于客户j的最晚服务开始时间且不小于0；式(22)表示车辆的载重量约束；式(23)和(24)为决策变量属性。

2 混合遗传变邻域搜索算法

本文设计了混合遗传变邻域搜索算法(Hybrid Genetic-Variable Neighborhood Search Algorithm, HG-VNSA)求解建立的模型，具体操作步骤如下：

Step1设置参数。

Step2生成初始种群。

首先用最近邻插入法生成一条染色体；然后用Logistic映射方程生成初始种群；最后把用最近邻插入法生成的染色体放在用Logistic映射方程生成的初始种群的前面，成为种群规模为pop_size的初始种群成。

Step3利用插入法生成车辆路径。

Step4计算所有染色体的适应度值。

Step5搜索当代种群中的最优染色体，若当前最优解优于历史最优解，则接受该染色体，否则，拒绝。

Step6本文采用0-1Exchange、1-1Exchange、2-OPT三种邻域操作改进当前解(具体邻域操作见2.6节)。本文还设计了以下两种自适应搜索策略：

(1)自适应邻域搜索次数

Si=「ε1·max_gen+⎣ε2·max_gen·(gen/max_gen)1/2」⎤

(2)自适应邻域搜索范围

Sr=「β1·n+⎣β2·n·(gen/max_gen)1/2」⎤,

β1+β2≤1,β1,β2≠0

其中，max_gen是预设的最大迭代次数，⎣x」表示取不大于x的最大整数，「x⎤表示取不小于x的最小整数。

Step7若解改进了，则返回第一个邻域结构继续进行搜索，否则执行下一个邻域结构进行搜索，直到最后一个邻域结构仍未找到改进解时，搜索终止。

Step8输出最优解。

Step9结束。

2.1 考虑时空距离的初始种群的生成

2.1.1 时空距离的定义与度量

本文将空间距离和时间距离归一化处理，计算公式如式(26)所示。

(25)

(26)

2.1.2 初始种群的生成及编解码方式

(1)采用最近邻插入法。选择模糊时间窗窄且EETi小的客户，若存在多个，则从中选择距离配送中心最近的客户作为第一个客户，然后根据时空距离采用最近邻插入法将其余客户依次加入到客户排列中。

(2)利用混沌系统的内在随机性，用Logistic映射方程进行迭代，生成初始种群，Logistic映射方程如式(27)所示:

xi+1=wxi(1-xi),i=1,2,3,…

(27)

其中xi代表第i时刻种群的状态，xi∈[0,1]，w是控制参数，w∈(3.5699456,4]。

具体的编码方式如图1所示。

图1 编解码方式示意图

2.2 适应度函数

染色体的适应度函数fi可以表示为:

fi=1/Ci

(28)

其中，Ci为染色体i的目标函数值。

2.3 选择操作

确定式采样选择策略的具体步骤如下:

Step1计算种群中每条染色体在下一代种群中的期望生存数目Fi:

(29)

其中，fi是染色体i的适应度值，pop_suze是种群规模。

2.4 拆分准则

2.5 时间优化策略

本文提出确定车辆最优出发时间的时差推移法(Time Difference Pass Method, TDPM)，给出以下定义：

定义1任一可行路径做任何调整都会造成路径在时间上的不可行或降低客户满意度，该路径称为紧路径。其确定方法如下：

(1)记录可行路径中车辆在客户规定时间窗之前到达客户点，客户点的个数ne，车辆在客户规定时间窗之后到达客户点，客户点的个数nl。

(2)可行路径中每个客户点的可能调整量可由式(30)进行计算，若ce·min{Δti}·ne≤cl·min{Δti}·nl，即ce·ne≤cl·nl，则该可行路径为紧路径。

(30)

2.6 变邻域搜索策略

本文采用的邻域结构为N={N1,N2,…,Ng,…}，首先让个体i从N1开始扰动，若未找到改进解，则执行N2；否则，令x=x′，并返回N1重新开始扰动，若到最后一个邻域结构仍未找到改进解，则停止搜索。本文的变邻域操作是0-1Exchange、1-1Exchange和2-OPT：

(1)0-1Exchange：分为线路内0-1Exchange和线路间0-1Exchange。随机选择客户i和客户j，将客户i插入到客户j的后面。

(2)1-1Exchange：分为线路内1-1Exchange和线路间1-1Exchange。随机选择客户i和客户j，交换客户i和客户j的位置。

(3)2-OPT：分为线路内2-OPT和线路间2-OPT。随机选择客户i和客户j，若客户i和客户j不同路，通过交换路径中部分边使其相邻，组成新的路径。

3 算例验证及结果分析

本文参数设置如下：最大迭代次数max_gen=100～1000，种群规模pop_size=20～100，自适应邻域搜索次数参数ε1=0.01～0.5，ε2=0.01～0.02，自适应邻域搜索范围参数β1=0.1～0.15，β2=0.2～0.4，控制系数w=4，时空距离参数a1=0.5，a2=0.5，α1=2.5，α2=0.95，α3=4.2。

3.1 VRPTW算例验证

实验1采用Solomon[15]的VRPTW标准算例进行实验，文献[16～19]的求解结果见表1和附表1。表1中“BKS”表示算例的已知最优解，“L”表示本文HG-VNSA的求解结果，“N”表示使用车辆数辆，“%Dve”表示本文HG-VNSA的求解结果相较于已知最优解的计算偏差。将Solomon计算的结果作为标准，把其他算法计算的结果进行“标准化”，即附表1中“rate”的数据均为与Solomon计算结果的比值，“Mean”表示各算例的比值平均值。

表1：HG-VNSA求出4个算例的已知最优解，与已知最优解的偏差最大为0.97%，最小为0.17%，均小于1%。分析结果表明HG-VNSA能够有效求解小规模VRPTW算例，具有较强的寻优能力。

附表1：HG-VNSA的比值平均值为5.23，均小于SMA、RMPC、AVNS、Modified ACS。分析结果表明HG-VNSA的可行性和有效性。

表1 小规模VRPTW算例对比结果

3.2 SDVRP算例验证

实验2选取文献[20]中的算例进行实验，文献[20～22]的求解结果见表2，本文HG-VNSA算法求出的最优路径见表3，其中“Best”表示各算法求出的最优解，“Mean”表示各算法求出的平均解，“CPU”表示各算法运行10次的平均运行时间,“R(loads)”表示行驶路径(各路径中各客户需求满足量)，“L”表示车辆行驶距离。

表2：HG-VNSA在10次计算结果中均求出最优解，具有较强的稳定性。HG-VNSA算法求出的平均值相较于其他算法最大改进了6.49%，最小改进了2.63%。

表2 不同算法的求解结果对比

表3 HG-VNSA算法求出的最优路径

3.3 VRPSDPTW算例验证

实验3文献[23]对Solomon[15]的VRPTW标准算例进行了扩展。本文选取扩展后的算例进行实验，文献[23]的求解结果见表4，文献[23～26]的求解结果见附表2。将Wang[23]采用GA计算的结果作为标准，把其他算法计算的结果进行“标准化”，即附表2中“”的数据均为与GA计算结果的比值。

表4：Cplex求出4个算例的最优解，GA和HG-VNSA也求出这4个算例的最优解。其余5个算例中，只有算例“RCdp2504”和“RCdp2507”，HG-VNSA的求解结果与GA相同，其余3个算例所求最优解与GA最大偏差0.30%，最小偏差0.09%。分析结果表明HG-VNSA具有较强的寻优能力。

附表2：p-SA求出6个算例的已知最好解，其中RCdp201改进最大。DCS求出9个算例的已知最好解，其中RCdp201改进最大，且有2个算例求出的最优解少使用一辆车。IGAFSA求出3个算例的已知最好解，其中RCdp208改进最大，且有3个算例求出的最优解少使用一辆车。HG-VNSA求出8个算例的已知最好解，其中RCdp205改进最大，且有3个算例求出的最优解少使用一辆车。从“”的数据可以看出：HGVNSA的比值平均值均小于p-SA、DCS、IGAFSA。分析结果表明HGVNSA能够有效求解VRPSDPTW大规模算例，验证了HGVNSA的可行性和有效性。

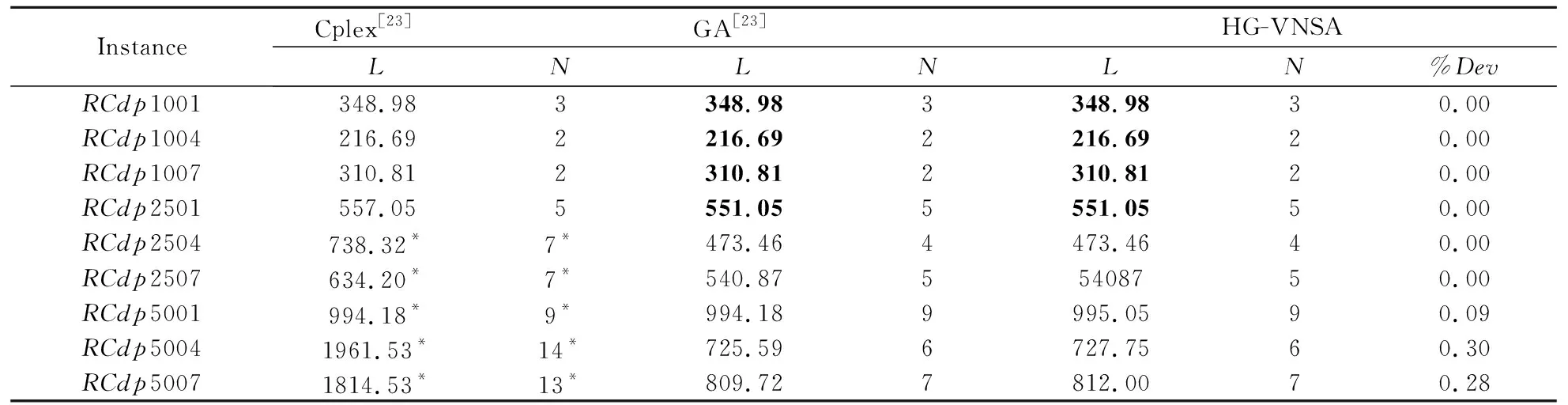
表4 VRPSDPTW中小规模算例对比结果

3.4 SDVRPSDP算例验证

实验4选取文献[27]的数据进行实验，结果见表5。

表5：需求允许拆分策略下的求解结果优于需求不允许拆分。在需求允许拆分策略下进行求解，HG-VNSA求出的最优解比蚁群算法少使用1辆车，且行驶距离缩短了0.05%。

表5 SDVRPSDP算例对比结果

3.5 SDVRPSDPTWP算例验证

实验5对3.3节中的VRPSDPTW标准算例进行修改，生成SDVRPSDPTWP算例。修改如下：EETi=ETi-60,ELTi=LTi+60，客户最低满意度ω=0.5，单位时间处理ξ=5单位的货物，单位时间等待成本ce=2，单位时间延误成本cl=3，单位理货成本cd=25，车辆的额定载重Q=200，单位派遣成本ck=100，空载油耗率z1=0.15，满载油耗率z2=0.23，油价co=6.5。实验结果见附表3，其中“C”为最优路径的总配送成本，“CPU”为程序运行时间。

附表3：使用枚举法只能求出算例规模为5和10的算例的最优解，使用HG-VNSA1和HG-VNSA2也能求出这些算例的最优解，在求解客户规模为10的算例时，使用HG-VNSA1和HG-VNSA2用时较少。本文设计的时间优化策略在总配送成本方面最大改进了19.653%，最小改进了0.001%，只有算例“RCdp203-15”使用时间优化策略前后的求解结果一样。