多商品分批次取送货的模糊需求车辆路径问题

高振迪, 计明军, 孔灵睿, 郭兴海

(大连海事大学 交通运输工程学院,辽宁 大连 116026)

0 引言

商品销售会因气候、经济、文化等因素产生库存不平衡现象，如区域性流感暴发可致附近药店库存断货，流感过后则可能出现库存积压，造成运营损失。连锁体制下，连锁店归总公司管辖，沟通门槛低，可通过店间调货提高闲置资源利用率，节约运营成本。目前，调货策略已成为连锁企业关注的热点。

多商品多批次取送货的模糊需求车辆路径问题(multi-commodity vehicle routing problem with split delivery and fuzzy demand, MCVRPSPDFD)是上述调货思想的延伸，可拆分为分批取送货车辆路径问题(vehicle routing problem with split pickups and deliveries, VRPSPD)和模糊需求车辆路径问题(vehicle routing problem with fuzzy demands, VRPFD)。Dror率先提出分批送货问题，研究指出，分批送货拓展了解空间，可降低配送成本。随后，研究者们逐渐将分批送货问题转换为供求匹配网络已知的VRPSPD问题。C. Archett等[1]提炼出该问题的经典公式，归纳了时间窗、分批次配送等变体问题。Marielle等[2]提出了单产品多次访问客户点的约束，现被广泛应用于工厂间的原料调配。多商品分批次取送货问题(multi-commodity vehicle routing problem with split pickup and delivery, MCVRPSPD)由Al-Khayyal等[3]提出，马艳芳等[4]在此基础上研究了模糊需求下同时取送货问题，通过将取货目标均视为出发点，实现问题的求解。近年来，研究者们开始探究供求网络未知的MCVRPSPD问题。供求网络未知指客户点间未形成牢固的供求关系，该问题由徐东洋[5]提出与完善，以协助烟草公司重新分配分厂的原料库存。由于该问题的相关研究常忽略配送过程中的不确定性，反而可能导致成本增加。在已有研究中，对于不确定问题的研究多基于随机理论。然而使用模糊理论描述不确定因素更贴合实际[6]。因此，张建勇等[7]定义了模糊需求车辆路径问题，通过引入决策者主观偏好值来限制模糊变量，节约配送成本。

1 问题描述与建模

1.1 问题描述

本文研究问题可描述为：一组对多货物产生三角模糊需求的连锁店，要求配送和/或运走不同种类的货物，服务由一队具有里程和容量限制的车辆提供，车辆可以多次访问客户点，在完成配送后需要返回仓库，企业希望运作成本最低。

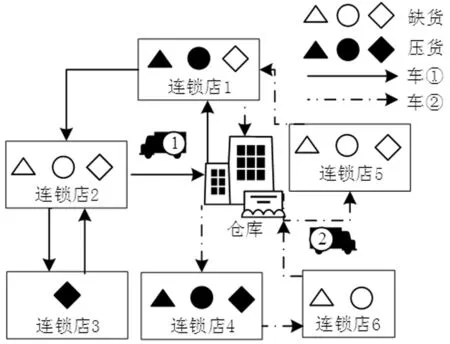
图1 MCVRPSPDFD优化方案

本文研究的优化方案示意如图1，车辆在不同需求模糊的店面(连锁店2、3)往返平衡商店库存，满足对应需求；当下一点(连锁店5)配送失败概率不被决策者接受时，车辆从当前位置(连锁店6)返回仓库取货再进行配送。

1.2 问题假设

①模型假设了一种场景：每一个连锁店都需要较大批量的补货，车辆需要在补货的同时顺带完成调货任务，故将里程约束转为容量约束；

②为方便商店库存管理，设每次访问至少满足某一种货物的需求。

1.3 模型参数

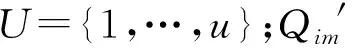
常量：Kmax为可用车辆数目；Q为车容量；M为趋于正无穷的数；C(R)为决策者偏好值；C0为油价；Ck为出车成本；C1为额外提取一单位货物付出的代价。

师：看来对AP 2=BP 2=AN·BM这一关系的发现也是制约我们解题和出题的原因，那我们现在会出题了吗？

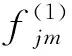
1.4 确定需求模型

确定需求模型以出车成本与里程成本最低为目标，其目标函数为:

(1)

约束条件:

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

∀j∈N′,b∈U,n∈P,k∈V

(14)

siajbmk≥0,∀i∈N,j∈N,a∈U,b∈U,m∈P,v∈V

(15)

(16)

(17)

(18)

(19)

qjbmk≥0,∀j∈N,b∈U,m∈P,k∈V

(20)

(21)

(22)

式(2～3)：任一车辆均从起点0出发并返回终点。式(4～7)：任一车仅能访问起点与终点各一次。式(8)：车辆访问任一点，都有访问次数对应。式(9)：对路线流进行约束，确保车辆的来源和去向。式(10～11)：消除子回路。式(12～13)：车辆从仓库空车出空车回，该式对于不同情境可做出相应改变，如后文提到的模糊需求，可设计为返回时车辆装载量的最大模糊数大于等于0。式(14)：装卸平衡约束，用以确保车辆装载货物等于原装载量与装/卸货量之差。式(15～16)：车辆在行驶时装载货物量不为负且不超过最大容量。式(17)：任意客户对货物的取/卸货量应与对的供/需相等。式(18)：被次访问的客户对货物供货时，车提货量应小于等于点供应量和自身容量。式(19)：被次访问的客户对货物需求时，车卸货量为点需求量或0。式(20)：任意一次服务的提卸货量均不为负。式(21)：车服务点的前提是到达点。式(22)：计算执勤车数。

1.5 模糊需求模型

模糊需求模型借鉴了曹二保[9]提出的可信度计算公式，目标函数为:

(23)

约束如下:

(24)

∀j∈N′,b∈U,k∈V,m∈P

(25)

(26)

(27)

(28)

(29)

2 遗传禁忌算法

鉴于目前鲜有学者研究针对MCVRPSPDFD问题的算法，在分别参考多货品、模糊需求、需求可拆分等车辆路径问题求解算法后，本文提出了一种改进的GTHA算法，其优势为：遗传算法的编码结构简单，操作便捷，种群修复与全局搜索能力强；禁忌搜索算法框架简单，局部搜索能力强，求解复杂车辆路径问题时不仅更加准确，还具有效率优势。算法设计思路如下(流程见图3):

①种群结构。在多次访问的条件下，未满足的客户会重复出现至被满足(图2)。范例中，客户均需日常补货，且有1种货物要调配，flag0对应补货，flag1对应货物1，值为1时表示对应需求被满足。②构建初始解。基于贪婪算法，对供货点进行单元化处理[5]，快速构建高质量初始解。③巡回路径编码。利用巡回路径法[10]进行二次编码，避免迭代产生无效解。④适应度。参考数学模型，通过容量约束计算出每一种群所需车辆数目和车辆对应客户点；将各费用之和(式23)取倒数得适应度。⑤禁忌算子。代替变异算子，邻域产生方式：交换两个基因的位置；藐视准则：当某个基因移动后得到的邻域解优于当前最优解，则不论该基因移动是否处于禁忌状态，都接受该解作为新的当前解和当前最优解。⑥选择算子。为提高求解效率，本文在轮盘赌选择方法的基础上引入了保留精英种群策略。⑦交叉算子。在两条父代染色体上随机选择长度相同的一段基因进行交叉。

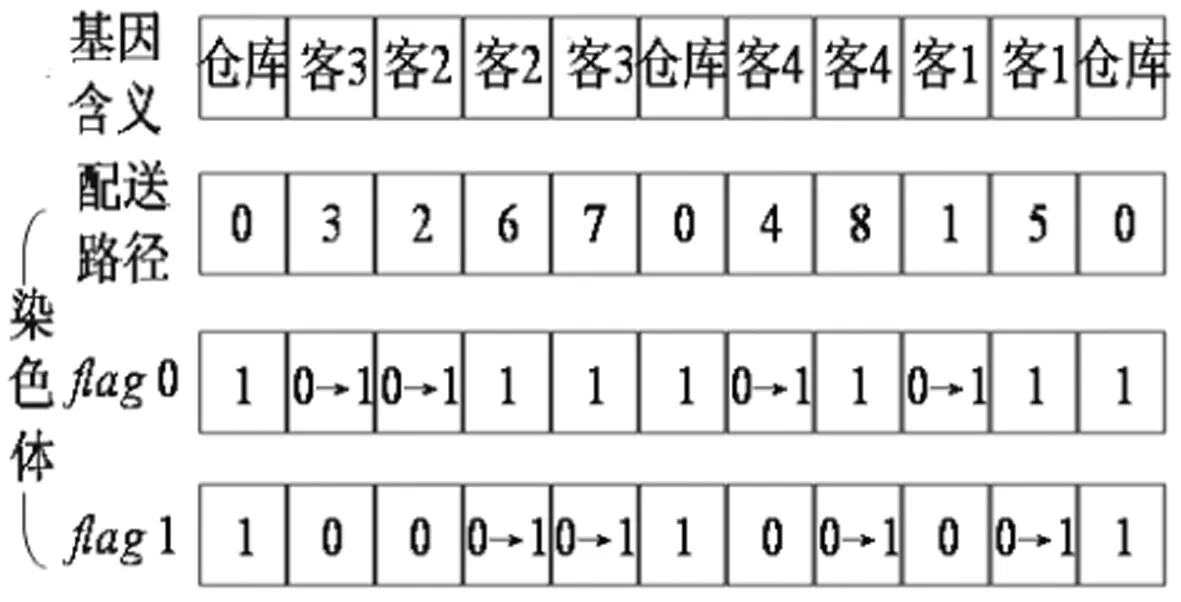
图2 种群结构示例

图3 算法流程图

3 算例求解

3.1 算例描述

本文构建了以某医药连锁公司为背景的算例如下：药品由工厂的仓库运往各连锁店，公司希望名下四台容量为150的车辆在配送的同时，将各连锁店滞压的2种高价值药品进行流通。出车成本80元/次；燃油成本0.4元/单位里程；配送失败时额外的调货成本10元/单位，算例坐标取自Solomon R101的1～20客户点(其中1点为仓库)，客户模糊需求由随机数生成。

3.2 算例结果

算例求解结果为：总成本683.8元，其中里程成本263.8元；额外提货惩罚成本180元；出车成本为240(3辆)元；车辆配送路径见表1。其中，多需求的点(如点10、5、8、9、6)有被一次性满足的倾向，因为可以缩减里程成本。

表1 车辆配送情况

3.3 参数测试

经测试，种群规模和TS算子迭代次数对GTHA算法影响最大，故通过实验研究参数选择对算法性能的影响，得到结果如图4，5。图4中，种群规模与算法收敛速度及求解效果呈正相关，种群规模超一定规模时对结果影响会变小，考虑到算法效率，本文种群规模取20个。图5可看出，TS算子收敛所需代数与问题规模呈正相关。故统计不同问题规模下，TS算子运算花费时间，得出耗时亦与问题规模呈正相关，故TS算子迭代取20次，以兼顾运算速度和运算效率。

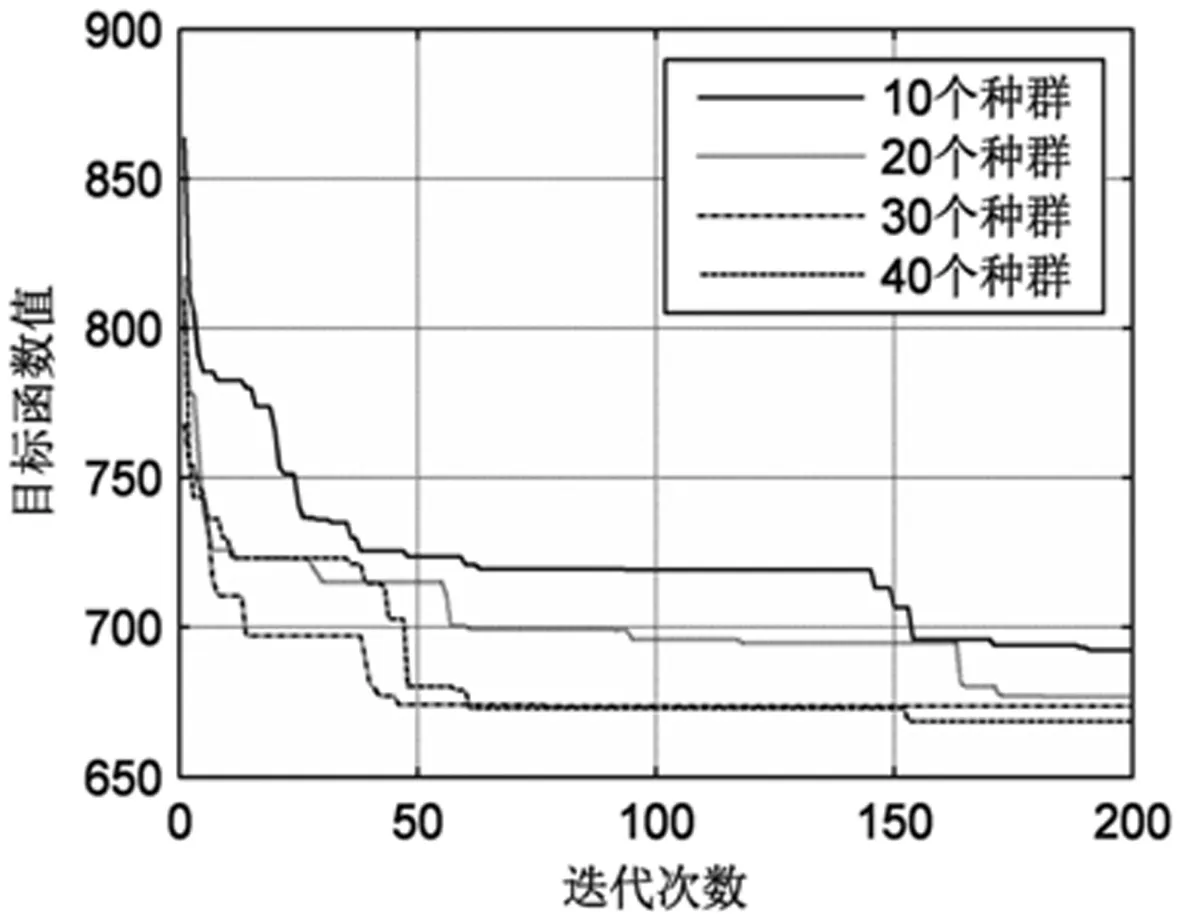
图4 GTHA算法收敛情况

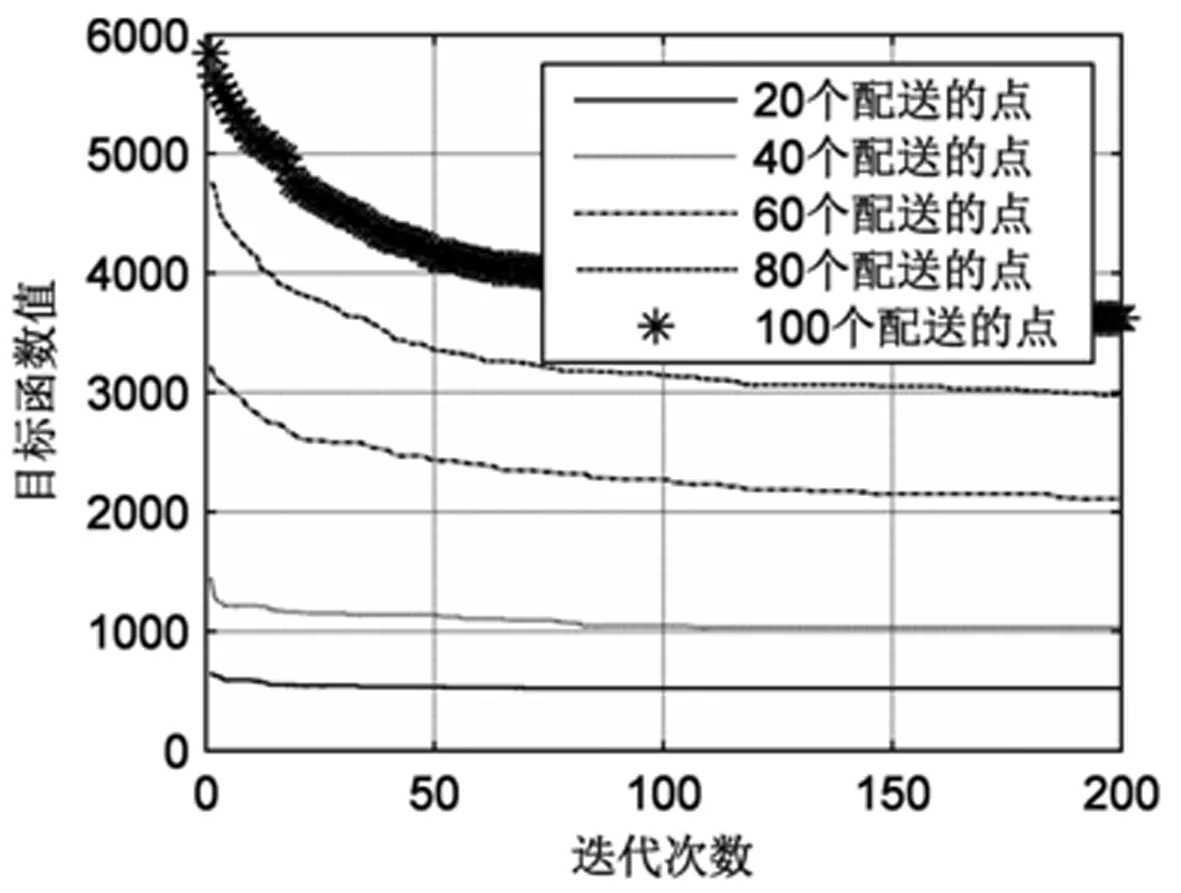
图5 TS算法收敛情况

4 算例分析

4.1 模型及算法验证

本文先验证算法求解确定模型准确性如表2。极小规模的问题中，GTHA算法求解结果与Cplex求得的最优解基本相同。对于更大规模的算例，由于解空间变大，Cplex很难在短时间内求出结果。

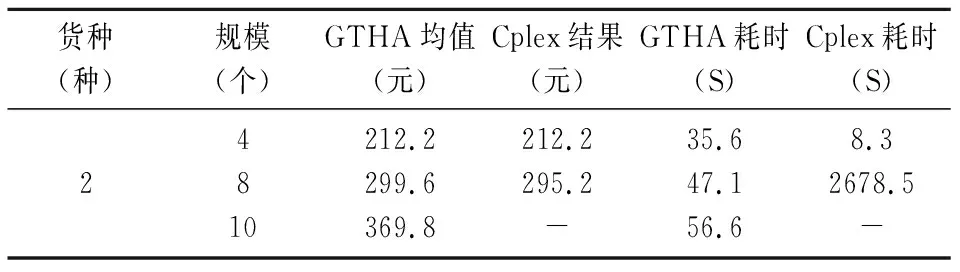
表2 Cplex对比结果

为探讨GTHA的可靠性，对不同规模算例进行100次求解得到变异系数(见表3)。可以看出，运算耗时与问题规模及货物种类呈正相关，且求解结果的变异系数低于6%，算法结果比较稳定。

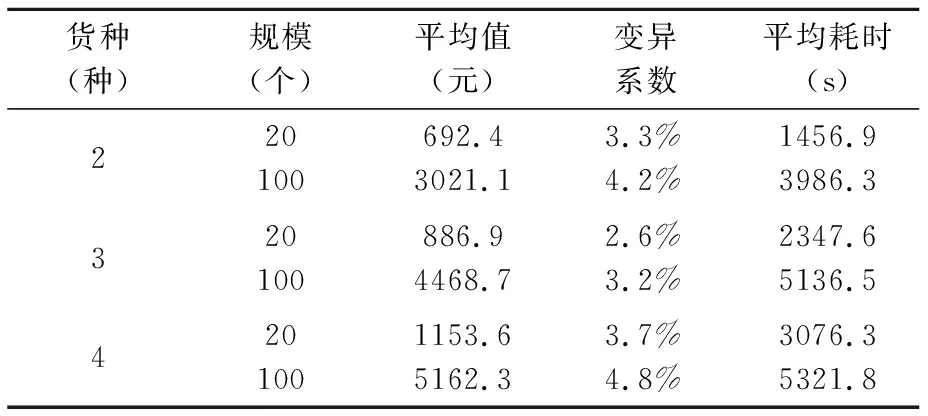
表3 变异系数

为验证GTHA算法效率，设计GA、TS算法对不同问题规模的对照试验，结果如图6所示。其中，GTHA算法求解效果最好，其次是局部搜索能力强的TS算法，最后是广域搜索能力强但局部搜索能力弱的GA算法。

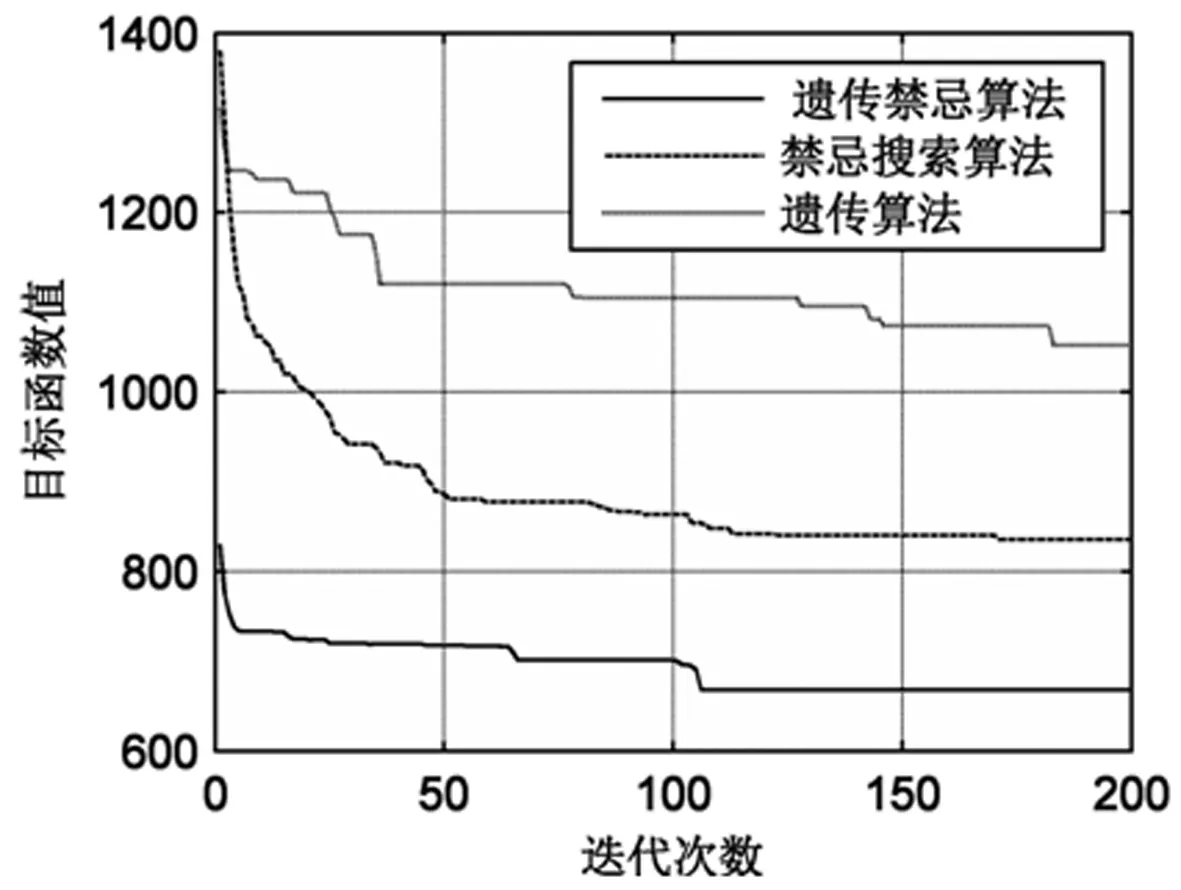
图6 三种启发式算法对照结果

4.2 结果比较及决策者偏好值分析

为验证分批次访问规则的优越性，本文对照调度规则：A. MCVRPSPDFD问题；B.模糊需求下单车单次访问客户点问题；C.允许配送失败的分批取送货问题。

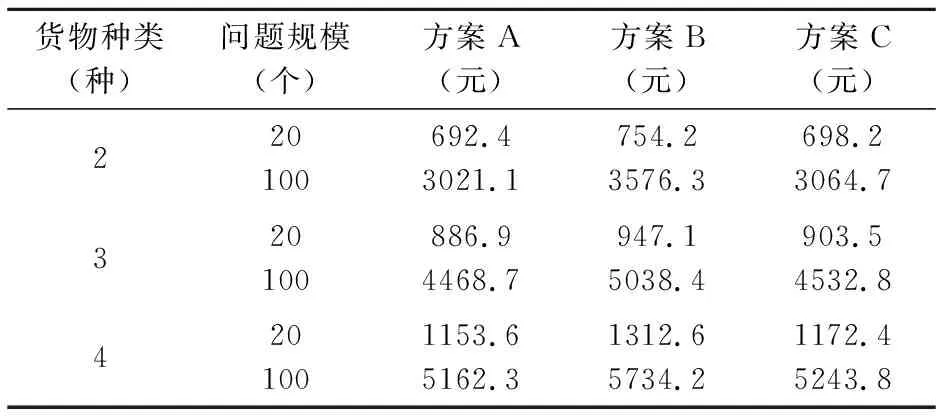
表4 对照试验结果

由表4可知，A、C方案均优于B方案，证明了分批取送货方案的优势。A方案优于C方案，在于A方案通过提前返回仓库补货避免了里程浪费。在各配送点距离很近时，A、C方案结果相差较小，这是由于未对配送失败设计额外的惩罚成本。实际中，连锁公司会考虑包括人员工时在内的多种惩罚成本，这会使A方案的优势更显著。

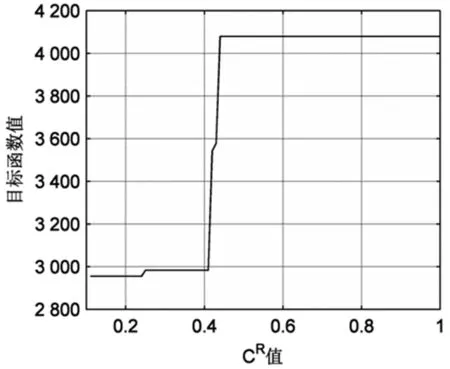
图7 总成本随 值变化趋势

C(R)值对车辆行驶路径有极大影响。对不同规模的实验结果进行分析，得某次实验C(R)值对总成本影响如图7。当C(R)值大于0.4时，车辆行驶总成本激增，这是因为随着决策者对配送失败的接受度降低，车辆配送失败次数会增加，总成本会随之增加至峰值。经试验，不同配送情况下激变点位置和激变程度不同。其中激变点变化范围在0.3～0.5之间，激变程度与连锁店提供货物的数量呈负相关。

5 结论

MCVRPSPDFD问题可以帮助连锁行业提升配送效率，降低配送成本。本文在研究该问题时，还考虑了配送时客户点需求的模糊性，以降低物流配送运作成本、提高物流配送服务水平为目标，构建了考虑多批次、多货物、取送货和模糊需求特点的车辆路径模型。考虑到问题复杂度，提出了改进的GTHA算法对模型进行求解，验证了模型和算法的有效性。结果表明，MCVRPSPDFD方案可帮助企业节省调拨费用；此外，方案成本会随决策者对配送失败的接受度而变化，决策者可根据对配送失败的接受程度选择最佳的值，以获得最优的配送方案。