超声导波缺陷检测仿真分析*

2022-12-14张鑫宇李忠虎关丽坤李婧

内蒙古科技大学学报 2022年1期

张鑫宇，李忠虎，关丽坤，李婧

（1.内蒙古科技大学机械工程学院，内蒙古包头 014010；2.内蒙古科技大学信息工程学院，内蒙古包头 014010）

超声导波检测技术相较于传统的超声波检测技术具有传播距离更远、速度更快、检测范围更广的特点，在板壳类和管道的无损检测中具有良好的应用前景[1，2].应用过程中，检测人员不仅需要检测出缺陷的存在位置，还需要获得缺陷的类型、面积、深度、形状等详细信息，根据缺陷的危险程度决定后期修复策略，从而提高检测和修复效率.研究人员围绕缺陷的识别开展了一些研究，但效果并不理想.

北京工业大学的何存富、刘增华团队选取管道、复合材料板等零件为研究对象，开展了超声导波的传播特性研究，从能量传播的角度分析声场分布[2].但并没有系统建立不同复杂缺陷几何特征与导波回波信号特性之间的关系，没有明确超声导波在复杂结构中的传播或与复杂缺陷的交互作用关系，未得到深度信息.北京理工大学的徐春广、李喜朋对变厚度板进行了超声导波研究，提出了基于激励S0模式，接收A0模式导波的缺陷识别及特征参数提取方法，由于理论分析中参数关系的人为简化，实验获得缺陷深度缺陷深度和回波信号特性参数声时差的关系与理论分析不能完全相符，存在一定误差[3].

针对超声导波检测中零件缺陷信息表征不足的问题，基于Lamb波中A0和S0模式导波，采用数值模拟对板类零件进行缺陷检测，对不同尺寸缺陷下超声导波在薄板中的传播进行模拟，找到A0和S0模式导波与缺陷深度的关系.

1 模拟仿真分析

1.1 有限元模型的创建

Lamb波是20世纪Lamb在研究无限大板中正弦波问题时发现的一种在自由边界条件下固体结构中传播的弹性波.当波以某角度入射到薄板时，在一定的材料密度、弹性系数、厚度及波动频率下可产生Lamb波.根据物质粒子运动方向和板结构中心轴是否对称，Lamb波传播方式可分为对称和反对称模式，2种模式都可独立在板结构中传播，其频散方程如下：

创建1个均匀材质的铝制薄板模型，采用ANSYS瞬态动力学，基于声场的分析[4，5]，用机械振动模拟超声波、进行薄板的超声导波检测的仿真模拟，模型选取Solid Quad4 node182单元类型，设定铝板的弹性模量E＝70 GPa，泊松比ν＝0.33，密度ρ＝2.7 g／cm3.铝板的厚度为0.001 m，长度为0.2 m.在划分单元中，为了保证计算的精度，单元的大小需要满足Le≤0.125λmin，λmin为铝板中的最小波长，Le为单元格的边长.根据导波在铝板内的横波的声速（CT＝3100 m／s）和激励所用到的频率（1 MHz）以及频率、波速和波长三者之间的关系，可以计算出最大的步长为0.3750 mm.而实验中，为了提高计算的精确度，设置模型的单元格的最大尺寸为0.2 mm，采用自由划分为矩形单元，如图1所示.

图1 整体网格模型

1.2 激励信号的选取

导波在铝板中传播会发生频散现象.便于信号的分析，一般使用模式少的导波来进行研究，而通过铝板的频散曲线图可知，随着频厚积数值的增加，导波的模式会变得复杂，因此在厚度一定的条件下，选择频率为1 MHz的激励信号.一般来说，频率低的信号传播距离大，但波长较大；而频率高的信号的波长较小，对缺陷的敏感程度较高.为提高分辨率，幅值增大为1000倍.

在仿真分析中，为了获得满足要求的单频窄带检测信号，通常需要对单频正弦信号加窗[5].通过分析几种不同的窗函数，为了使激励信号在传播过程中尽可能降低频散现象，一般用多个单频加窗函数作为激励信号，考虑到信号的检测、读取、后处理分析等，这里选择频率为1 MHz汉宁窗函数作为激励信号的窗函数，其表达式如下：

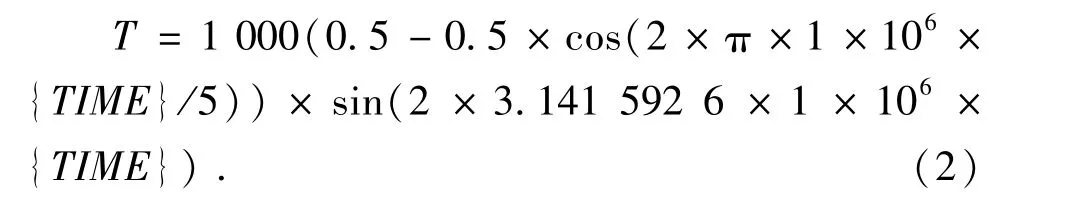
经过多次模拟与分析，得出激励信号的选择在3～5个较为合适，在实验中，采取窗口函数分段的模式.在时间0≤T≤5×10-6时，选择5个汉宁窗函数作为激励信号.

采用单方面的模式激励铝板的上表面，铝板中会同时存在A0模式波和S0模式波，但若采用双面同向激励方式时，铝板中只会存在A0模式波，而如果选取双面反向的激励模式，铝板中就会只存在S0模式波.由频散曲线可知，频厚积为1 MHz·mm的铝板内传播的信号只有A0和S02种模式存在，所以选择单面模式下，激励出A0波和S0波.如图2所示，选择在模型的左上角Y方向加载激励信号，而在模型的右下角加载全约束.

图2 约束和加载模型

1.3 求解设置

设置求解控制涉及定义分析类型、分析选项以及载荷步设置.执行完全法瞬态动力学分析，可以使用求解控制对话框进行这些选项的设置.

设置载荷步终点时间为155μs，时间步长为40 ns.在Frequency选项中，选择加载每一载荷步.确定之后，进行瞬态求解.

求解结束后，观察结果，选择时间历程后处理，设定变量为时间，然后定义位移变量.选取结果的Y方向位移，接着拾取模型上需要检测的点，以观察该点的信号随时间变化的波形图.

2 仿真分析

2.1 检测信号的分析

对没有缺陷损伤的板进行检测作为初始对照组，选择铝板上表面距离左上端激励点0.06 m处为探测点.

经过时间历程后处理，可得到该点的检测信号波形图，可以看到导波在检测点位置随时间的变化趋势.虽然这里能较为清楚的看到直达波和反射波的波峰，但具体精确的幅值和时间定位在这里比较难以读出.利用MATLAB软件进行具体的数值读取和分析，如图3所示.

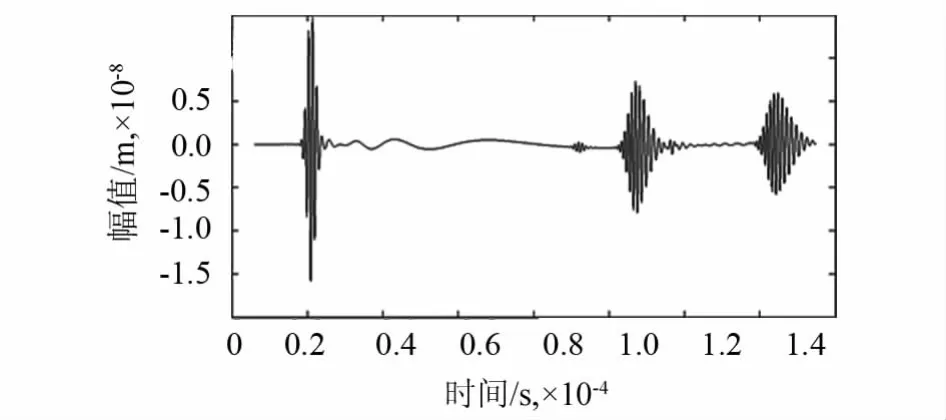
图3 检测信号图

波峰坐标信息如表1所示.

表1 信号波峰数据表

2.2 Lamb波对铝板缺陷位置的确定

在进行缺陷位置确定的检测实验中，可以通过计算导波的群速度来推算缺陷的存在位置.而导波的群速度计算一般是通过波包的传播时间除以波包的传播距离得到的，为了使实验数据准确和易于采集，选择波包的峰点作为计算的依据.计算公式如下：

式中：L为导波的传播距离，m；t，t0为该点波包峰点所在的时间，s.

在信号图中可以看到，A0模式的信号幅值要比S0模式的大很多，这是因为在相同激励源条件下，A0模式的信号的能量比S0模式下的信号的能量要大.而且S0信号的初始入射波耦合在了A0信号入射波中，不能准确的探测到波峰时间.因此在进行缺陷位置对比实验中，只通过A0信号来进行分析.经过计算，A0波的群速度为VA0＝3267.97 m／s，与频散曲线中得到的A0模式cg下，导波信号的群速度基本相符.

经过上述的分析与准备，进行用超声导波对铝板缺陷位置确定的仿真实验.

首先，在之前所建的没有缺陷的模型基础上，建立一个宽度为0.0002 m，深度为0.0005 m大小的缺陷.缺陷位置设置在距离左端上表面激励点0.14 m的处.

接下来对该模型进行划分单元、施加载荷、进行求解控制与瞬态求解.进入时间历程处理后，在该模型上表面依次选择距离左上端激励点0.010，0.020，0.030 m……一直到0.1 m的位置为探测点，进行对照实验.不同位置探测点的检测信号图如4所示.

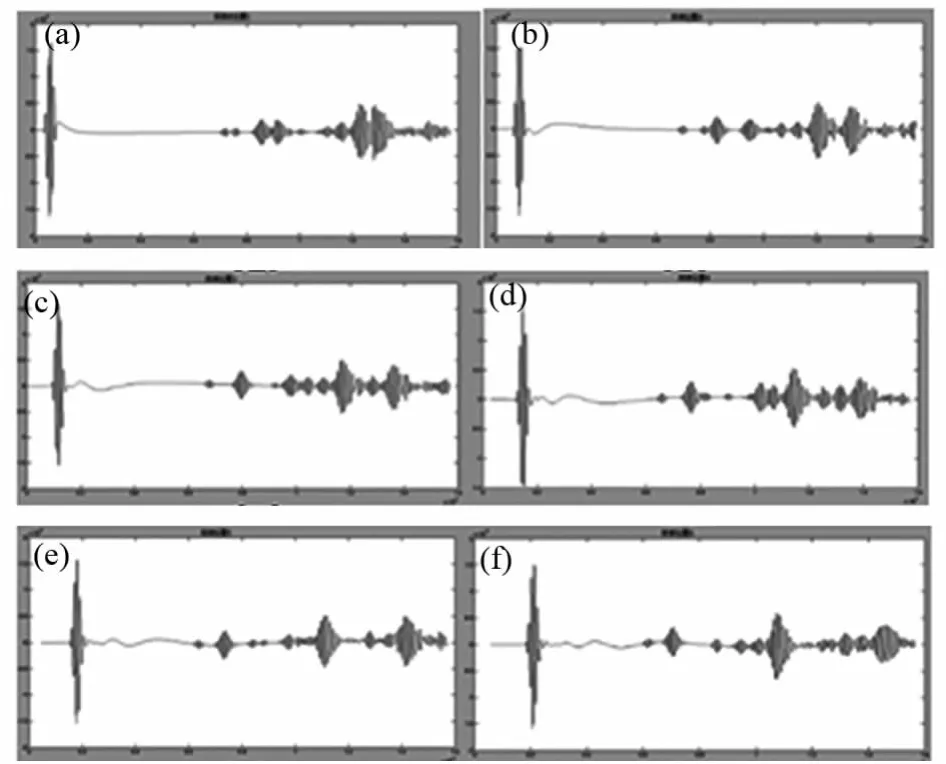
图4 不同探测位置的超声导波检测信号图（a）～（j）分别为距离左上端激励点0.01，0.02，0.03……到0.1 m的位置选取探测点的回波信号

通过分析不同探测位置的信号检测图，可以看到A0波与S0波波包位置，其波包出随时间的变化.这里只分析缺陷的位置信息，因此在整理数据时这里只读取A0波入射时波包包峰的时间，缺陷反射回来A0波波峰的时间和底板反射回来A0波波峰的时间.具体数据如表2所示.

表2 不同探测位置下信号波峰信息

缺陷位置的公式经过推算，可得：

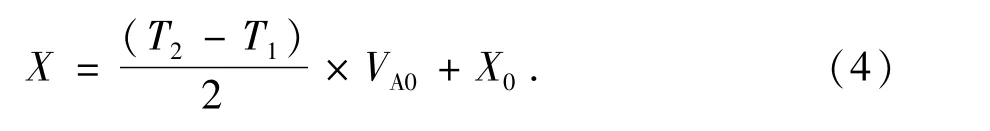
式中：X为缺陷距离左上端激励点的水平距离，m；T1为A0波入射波峰时间，s；T2为缺陷反射A0波峰时间，s；X0为探测点距左上端激励点的水平距离，m.

经计算，探测点探测到的缺陷位置如表3所示.

表3 不同探测点计算出的缺陷位置

如数据显示，经超声导波仿真模拟探测出的缺陷的位置与设置缺陷的位置在误差范围内是相符的.基于此，可以利用超声导波技术对铝板中的缺陷距离激励点的直线距离作出确定.

2.3 二维平面上对铝板的缺陷位置的确定

在实际探测中，通常还需要在二维平面上对铝板的缺陷位置作出确定，选择用圆弧定位的方法，即选择2个不同探测点，分别计算其与缺陷位置的直线距离，以探测点为圆心，以探测到的直线距离为半径做圆，在铝板上得到的交点即为缺陷的位置，如图5所示.

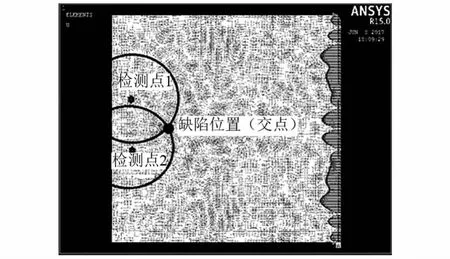
图5 二维的缺陷位置

对于利用超声导波对铝板中缺陷的大小进行判定，通过比对不同缺陷直径下信号的变化，对缺陷的直径大小做出分析.把缺陷位置设置在左上端激励0.14 m的地方，缺陷深度设置为0.0005 m，检测点位于上表面离左上端激励点0.06 m的位置.铝板缺陷的直径依次设置为：0.0002，0.0004，0.0006，0.0008，0.0010，0.0012 m.经过瞬态分析，时间历程后处理，得到了缺陷直径不同条件下检测的信号变化.具体数据如表4所示.

表4 不同缺陷直径的信号波峰信息（单位：m）

经过数据分析可以发现，随着缺陷直径的增大，A0入射波信号在检测点的位置并没有发生明显的变化，而A0模式下的波在经过缺陷和底板的反射后，它们的幅值信号变化趋势为先增大后减小，如图6所示.而S0模式下的缺陷反射波在检测点位置的幅值信号变化为先减小后增大.底板回波幅值信号则与A0模式下相同，即先增大后减小，如图7所示.当缺陷深厚比为50%时，缺陷直径增至波长的30%A0模式缺陷反射信号振幅开始减小，S0模式缺陷反射信号振幅随着缺陷直径增大而减小，当缺陷直径增至波长的30%时振幅开始快速增大.

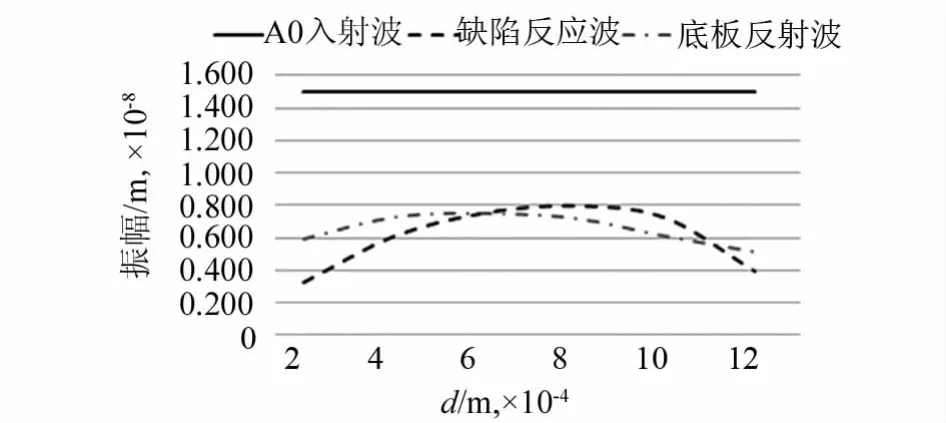
图6 A0波幅值随缺陷直径变化曲线

图7 S0波幅值随缺陷变化曲线

2.4 Lamb波对铝板缺陷深度的确定

利用Lamb波，还可以对试件中缺陷的深度进行确定.与之前所做实验基本步奏相同，这里其它条件都不变，只改变缺陷大小的深度作为对照组，将缺陷设置在离左上端激励点0.14 m的位置处，缺陷直径为0.0002 m，深度依次设置为0.0002，0.0003，0.0004，0.0005，0.0006，0.0007，0.0008 m，在距离左上端激励点的上表面0.05 m处设置探测点，观察和分析得到的信号图.

A0波和S0波第一次缺陷回波峰值坐标，如表5所示.

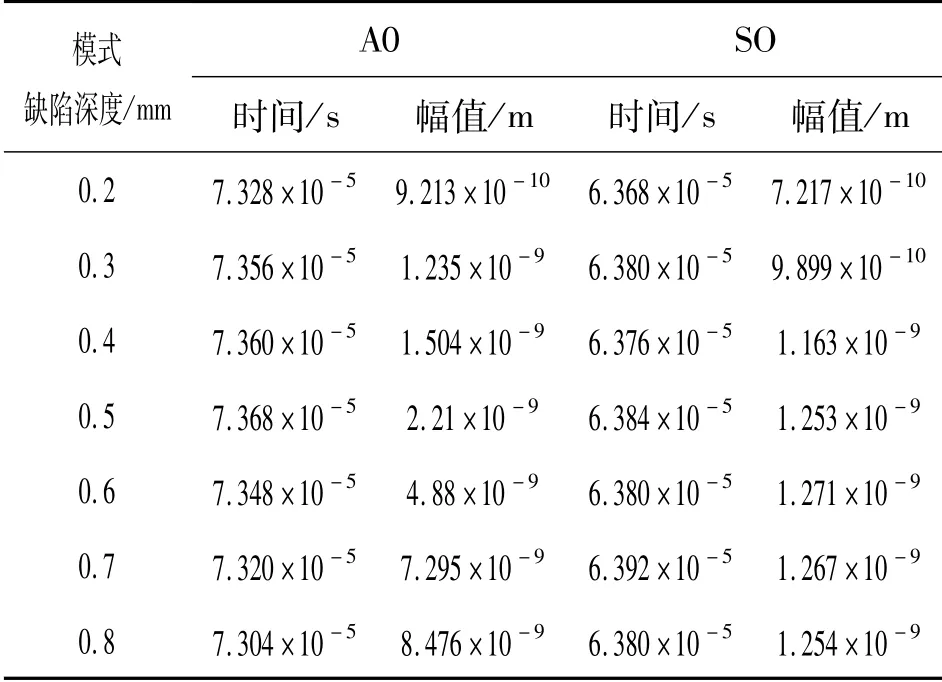
表5 不同缺陷深度下信号波峰信息

A0模式和S0模式的波形幅值随缺陷深度变化的曲线分别如图8，9所示.

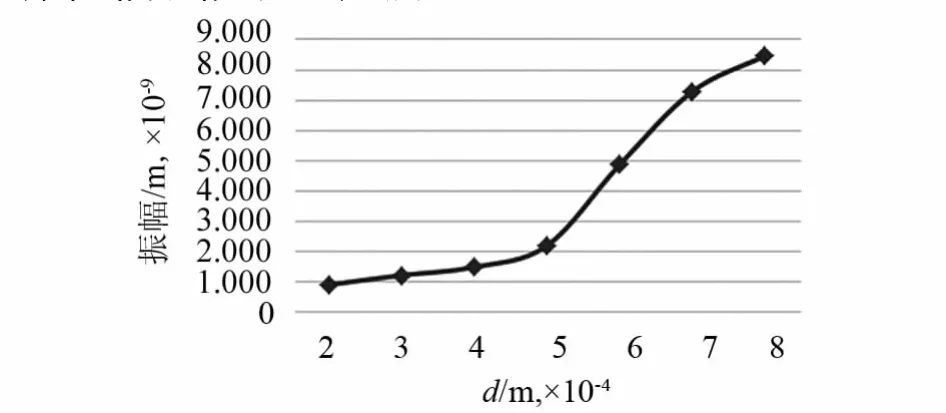
图8 A0波幅值随缺陷深度变化曲线

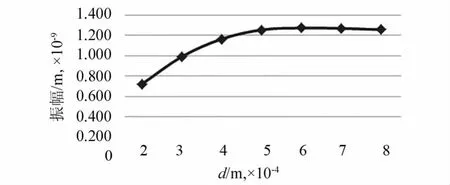
图9 S0波幅值随缺陷深度变化曲线

经过数据分析，发现随着缺陷深度的增加，A0和S0回波信号的幅值整体趋势都是不断增加的，在缺陷深度达到40%时，A0信号其反馈回来的信号幅值增大率会突然变高；而S0回波信号的幅值增大到一定程度后会趋于平缓，这里笔者推测因S0波的能量较弱，其反射波反馈的信号在达到一定程度后便保持不变.由于在实际应用中，探测的试件大小和缺陷大小会远大于实验中模拟的大小，而用导波探测工件的缺陷，一般在远距离探测中得到的数据更为精确，所以本次实验只能得出导波探测试件缺陷的大体过程和原理，未对其进行精确量化和公式推导.