基于摄动理论的直流微电网下垂系数优化方法

2022-12-13刘盈杞张新慧姜淞瀚

电力系统自动化 2022年23期

刘盈杞，彭克，张新慧，邢琳，姜淞瀚

（山东理工大学电气与电子工程学院，山东省淄博市 255000）

0 引言

随着中国“碳达峰·碳中和”目标的提出，光伏、风电、储能以及电动汽车等构建的微电网日渐受到关注［1-3］。相较于交流微电网，直流微电网无须考虑无功功率和频率问题，能够有效隔离交流侧扰动和故障，系统运行可控性及可靠性大大提高［4-6］。此外，直流微电网能够减少变流环节和换流器的使用数量，降低功率损耗和成本，提高供电效率。因此，直流微电网的研究和发展受到了国内外学术界和工业界的广泛关注［7-9］。

但直流微电网缺少旋转惯量，易受扰动而失稳，如何提高直流微电网稳定性问题成为目前研究的热点［10-12］。文献［13］通过建立z平面下的直流微电网小信号模型，针对主从控制模式下直流微电网小扰动不稳定问题，提出了一种由比例补偿器和带通滤波器组成的集中式振荡抑制控制器来提高系统小扰动稳定性。下垂控制作为微电网典型控制方法之一，相较于其他控制方式无须通信设施。当微电网运行模式发生变化时，无须改变可调度控制策略，因而下垂控制应用于微电网更具灵活性［14-16］。文献［17］采用混沌粒子群算法对下垂控制器参数进行优化，实现分布式储能系统间功率的合理分配。文献［18］通过对微电网建立小信号模型进行稳定性分析得出控制参数稳定边界。在此基础上，采用人工鱼群算法对微电网进行功率初次优化和二次优化，解决各分布式电源输出一致性问题。以上文献均是对下垂控制的AC/DC 逆变器进行分析。文献［19］针对直流微电网中传统功率-电压（P-U）下垂控制缺乏惯性、容易失稳的问题，提出一种基于P-U下垂特性的虚拟直流电机（virtual DC motor,VDCM）控制策略，提升了母线电压动态稳定性，抑制直流母线电压波动。上述文献通过补偿环节提高下垂控制下DC/DC 变流器稳定性，而并未涉及针对DC/DC 变流器下垂系数对系统稳定性的影响和优化问题。

目前，在微电网实际工程中，大都采用试凑法对控制系统进行调试。当换流器数目增加时，系统调试难度明显增大，试凑法须反复尝试，过程盲目、烦琐［17］，无法分析参数变化对系统的影响，且动态性能、安全裕度等无法计及。本文针对DC/DC 变流器下垂系数优化问题建立了直流电流-直流电压（Idc-Udc）下垂控制下的直流微电网小扰动模型，提出了一种基于矩阵摄动理论的DC/DC 变流器下垂系数协调优化控制方法。综合考虑特征根分布、阻尼比和稳定裕度等因素，通过对下垂系数摄动分析，得出下垂系数变化对系统状态矩阵的影响规律，将求取的特征值增量应用于算法优化迭代过程，避免了优化过程中特征值反复求解以及矩阵反复形成的问题，在保证精度的前提下，计算速度明显提高。最后，通过算例仿真和实验验证了该方法的有效性。

1 直流微电网系统结构及建模

1.1 外电路建模

直流微电网是连接多个分布式发电单元、储能装置和负荷的小型供用电网络［20］。附录A 图A1 为典型直流微电网结构，主要由以下5 个部分组成：1）储能电池和燃料电池通过下垂控制的DC/DC 变流器连接到直流母线；2）外部交流大电网通过AC/DC 逆变器连接到直流母线以实现交直流电网之间的功率交换，对恒功率控制下的并网DC/AC 逆变器在进行小扰动分析时，可视为一种输出功率为负的特殊型恒功率负荷；3）光伏发电单元通过采用最大功率点跟踪控制方式的DC/DC 变换装置连接到直流母线，建模时等效为恒功率负荷；4）负荷，包括电阻性负荷以及恒功率负荷；5）供电线路。

外电路模型详细推导过程如附录A 式（A1）至式（A4）所示。因此，外电路状态空间方程为：

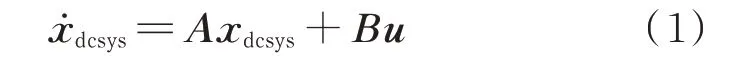
式中：xdcsys为外电路状态向量；ẋdcsys为xdcsys的一阶导数；A为外电路状态矩阵；B为外电路输入矩阵；u为外电路输入向量。其中，xdcsys、A、B、u的表达式分别如附录B 式（B1）至式（B4）所示。

1.2 控制系统建模

直流微电网中，光伏发电采用最大功率跟踪策略实现对太阳能的最大利用；逆变器连接外部电网采用恒功率控制；连接可调度分布式电源和储能电池的变流器采用下垂控制，Idc-Udc下垂控制原理如附录A 图A2 所示。

根据附录A 图A3 所示的换流器控制电路模型，详细推导过程如式（A5）至式（A7）所示，控制系统的小信号模型为：

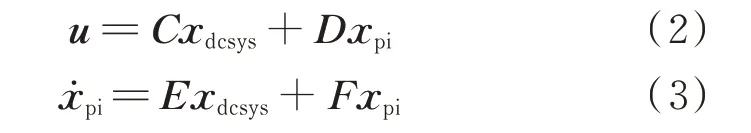
式中：xpi为控制电路状态向量；ẋpi为xpi的一阶导数；C、D、E、F为控制电路状态的系数矩阵，其具体表达式分别如附录B 式（B5）至式（B9）所示。

1.3 直流微电网建模

通过对直流微电网外电路和控制电路建模分析可知，直流微电网为非线性模型，联立式（1）至式（3）可得整个直流微电网的状态空间方程为：

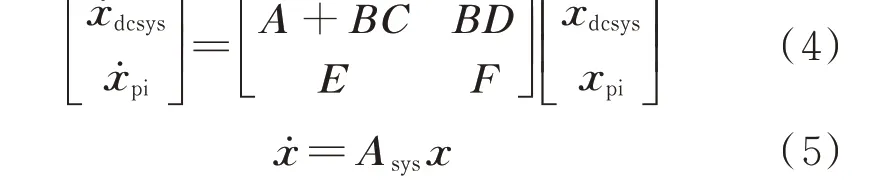
式中：x为系统状态向量；ẋ为x的一阶导数；Asys为系统状态矩阵。x的表达式如附录B 式（B10）所示。

据李雅普诺夫线性化理论，状态矩阵Asys的特征值决定了直流微电网的稳定性，该稳定性为系统局部渐进稳定性。若全部特征值实部都为负数，则系统是稳定的；若存在至少一个特征值的实部为正数，则系统是不稳定的。

2 下垂系数摄动分析

本章主要通过引入矩阵摄动理论研究下垂系数变化对直流微电网稳定性和暂态响应的影响，通过对下垂系数进行矩阵摄动分析，研究下垂系数对直流微电网的影响方式和程度。

传统特征值分析方法通过QR 算法求解特征值，每修改一次参数，需要重新形成并计算一次特征矩阵，计算过程烦琐、计算速度慢，且无法了解下垂系数变化对系统动态特性的影响形式和影响程度，因此，无法进行参数变化理论分析。通过矩阵摄动理论对下垂系数进行摄动分析，一方面，当参数摄动引起表征系统特性的系统状态矩阵发生变化时，通过矩阵摄动理论求出的特征值满足精度要求，避免了矩阵的反复计算和求解，能够实现直接快速求解；另一方面，对下垂系数进行摄动分析的过程中可以详细研究下垂系数对系统结构特性的影响方式和程度，便于直观研究和分析下垂系数变化对系统的影响，有利于对系统结构进行深入分析和优化设计。

2.1 矩阵摄动理论

对某一振动系统列写矩阵形式的自由振动运动方程为：

式中：U为刚度矩阵；V为质量矩阵；vr，q为特征向量；Λ（λ）为对角矩阵；λ为特征值，λ=ω2，其中，ω为系统振荡的固有频率。

当振动系统的某一参数发生改变时，U和V分别变化为：

式中：U0、V0、Asys0为原系统相应的矩阵；U1、V1、Asys1为参数变化引起的系数相应矩阵的变化矩阵；ε为摄动参数。

在工程上，当参数摄动量小于15%时，一阶摄动特征解可以满足一定的精度要求；当参数摄动量在15%～30%时，采用二阶摄动计算结果可满足精度要求；当参数摄动量大于30%时，需要用到更高阶的摄动计算。因此，在参数摄动过程中，如果参数的改变量不大，只需要考虑一阶摄动量即可［21］。

2.2 直流微电网状态矩阵的下垂系数摄动分析

为研究下垂系数对状态矩阵的影响，将下垂系数作为摄动参数，对直流微电网状态矩阵构造进行摄动分析，将系数矩阵分成多个模块进行处理。由于直流微电网的结构特点决定了系统特征矩阵的稀疏性和分块性，当进行下垂系数摄动分析时，只有少数元素会发生变化。

由于系数矩阵D、F中不含kr，i，其中，kr，i为第i个下垂控制中DC/DC 变流器的下垂系数。考虑到B摄动的微弱性通常不会引起系统特征值问题的质变［21］，在进行下垂系数摄动分析时，将B、D、F视为常系数矩阵。而直流微电网小扰动模型中，系数矩阵C、E均含有kr，i，矩阵A中部分元素为kr，i的隐函数，因此，需要对系数矩阵A、C、E进行深入分析。考虑到系数矩阵A中受kr，i摄动影响的相关矩阵元素均为kr，i的线性函数，可将各系数矩阵表示为：

式中：F、G、H分别为矩阵A、C、E的另一种有关下垂系数的表达形式；Fi、Gi、Hi为仅与第i个下垂系数相关的常数矩阵，i∈{1，2，…，N}，其中，N为下垂控制的DC/DC 变换器的个数；F0、G0、H0为与下垂系数无关的常数矩阵。

将式（10）至式（12）代入系统状态矩阵可得：

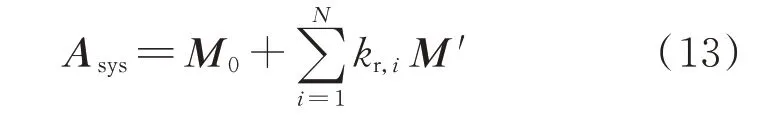
式中：M0和M'为与下垂系数kr，i无关的常数矩阵，具体表达式分别如附录B 式（B11）和式（B12）所示。

综上所述，在直流微电网中，下垂系数摄动对系统状态矩阵的影响区别于交流微电网：交流微电网会产生一次项、二次项和交叉项的表达式，不适合将摄动理论应用于算法迭代过程；而直流微电网只有下垂系数一次项会对系统特征矩阵产生影响，不会产生二次项、交叉项及更高次项的表达式。这是因为DC/AC 逆变器和DC/DC 变流器的下垂控制方式不同。因此，DC/DC 变流器更适合将摄动理论应用于算法迭代流程。

3 下垂系数协调优化

3.1 下垂系数优化目标函数

由于直流微电网本身惯性较小，针对传统下垂系数遭受扰动影响后更容易引起振荡失稳的问题，提出基于小扰动稳定的目标函数如式（14）所示，包括系统渐进稳定性、稳定裕度和阻尼比这3 个指标。

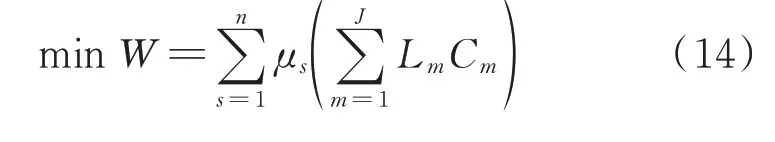
式中：W为总目标函数；μs为运行状态s的权重系数；n为运行状态的个数；Lm为子目标函数m的权重系数；Cm为子目标函数m；J为目标函数的个数，取值为3，综合考虑了系统渐进稳定性、稳定裕度和阻尼比3 个子目标。下面将对Cm展开介绍。

1）系统渐进稳定性。C1表示系统局部不稳定时，由大于0 的特征值所组成的部分，如式（15）所示。渐进稳定是保证其他2 个子目标函数的基础，因此，L1权重系数占比最大，取值为0.6。

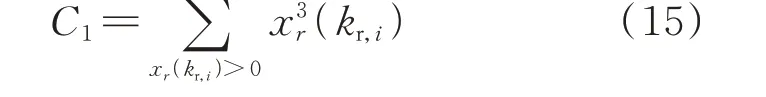
式中：xr（kr，i）为第r个实部为正的特征值。

2）稳定裕度。由于直流微电网运行场景的随机性与多变性，且直流微电网中产生扰动的因素较多，导致系统参数偏离设定值，直流微电网需要具备一定的稳定裕度，提高系统抗干扰能力。考虑到稳定裕度是建立在系统稳定性的基础上，L2的取值为0.2。C2表示系统低稳定裕度小于给定特征值实部的组成部分，如式（16）所示。

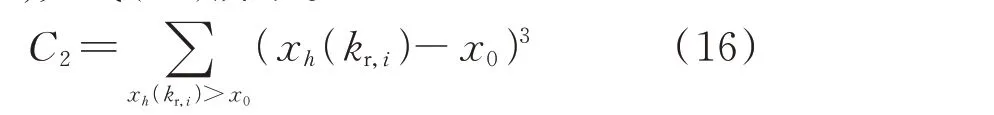
式中：x0为给定实部（x0为负数），取-1；xh（kr，i）为第h个实部大于x0的特征值。

3）阻尼比。直流微电网中存在多种电力电子装置之间相互作用造成扰动后调节时间太长的问题，因此有必要提高系统阻尼比来减小暂态过渡时间。在二阶系统中，当系统阻尼比太小时，调节时间越长，系统暂态过渡时间越长［12］。考虑到系统阻尼比是建立在系统稳定性的基础上，因此L3的取值为0.2。

在高阶系统中，涉及阻尼比时，通常考虑特征值中最靠近虚轴的共轭负数对。若这样的负数对仅有一对时，可将二阶系统代替高阶系统进行阻尼比分析；当出现多对共轭负数时，可将几个二阶系统串联代替高阶系统进行分析。C3表示系统弱阻尼时，小于给定阻尼比的组成部分，如式（17）所示。

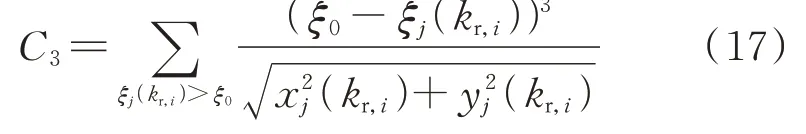
式中：ξ0为给定阻尼比，取0.1；ξj（kr，i）为第j个小于ξ0的阻尼比；xj（kr，i）为ξj（kr，i）的实部；yj（kr，i）为ξj（kr，i）的虚部。

3.2 协调优化算法流程

针对3.1 节中提出的基于渐进稳定性、稳定裕度与阻尼比的目标函数，通过控制特征值来实现下垂系数协调优化，附录C 图C1 为下垂系数协调优化流程，该流程主要由以下几部分构成。

1）输入初始特征值

建立直流微电网小扰动模型，列写状态空间方程构成矩阵Asys。通过计算初始潮流，并将其代入系统状态矩阵获取其初始特征值。

2）设定阈值

由于矩阵摄动理论中参数摄动量不能过大，大量实践证明，当参数摄动量小于10%时，通过矩阵摄动法所求特征值与QR 算法求解的特征值均在10%以内，满足精度要求。因此，设置每次迭代过程中对下垂系数的最大变化范围为10%［21］。

3）下垂系数摄动

采用序列二次规划算法求目标函数的最小值问题。该算法是在每个迭代点x（k）处构造一个二次规划子问题，通过将该子问题的解作为迭代搜索方向进行一维搜索，表达式为：

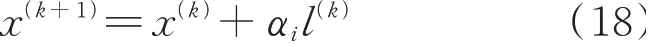
式中：x（k）为第k次迭代点；αi为每次迭代增量；l（k）为迭代的搜索方向。

通过式（18）可得x（k+1），重复上述迭代过程，直至最终逼近原问题近似约束最优点x*。此时，下垂系数随之逐渐逼近下垂系数最优解。

4）更新系统参数

由于每次下垂系数迭代造成系统潮流和相关参数对应发生改变，需要对系统参数进行更新。

5）更新目标函数

通过更新目标函数，利用序列二次规划算法进行寻优，将式（14）所示的目标函数进行泰勒展开如式（19）所示。

6）迭代终止判断

通过迭代次数是否最大或者目标函数是否为0来判断是否可以终止迭代。

4 仿真验证

为了验证上述下垂系数协调优化结果的正确性，在Simulink 中搭建了如附录A 图A1 所示的直流微电网的仿真模型，外电路参数如附录D 表D1 所示。通过负荷和分布式电源出力变化分析直流微电网小扰动动态稳定性。直流微电网初始特征值如表D2 所示，此时，系统特征值实部均为负数，即特征根都位于虚轴左侧，可判定该系统初始状态为稳定系统。

4.1 负荷扰动对直流微电网的影响

采用第2 章所示的直流微电网模型，在1 s 时，施加第1 次小扰动，电阻性负荷切掉40%；在6 s 时，施加第2 次小扰动，恒功率负荷增至原来的2 倍；在10 s 时，仿真结束。

4.1.1 负荷扰动优化过程分析

图1 为迭代过程中下垂系数目标函数值的变化情况。前8 次迭代的目标函数变化值较大，这是由所设定的子目标函数和初始下垂系数值共同决定的。当设置较大下垂系数初始值时，系统难以满足稳定性指标，且子目标相对权重系数L1明显大于L2，因此，造成初始状态下C1的取值较大，进而造成W取值较大。

图1 参数优化过程中的目标值Fig.1 Objective value in parameter optimization process

随着迭代次数的增加，直流微电网小扰动逐渐趋于局部稳定，此时C1为0，但C2和C3并不为0，下垂系数继续进行迭代优化，但调节速度明显降低。随着下垂系数不断优化，目标函数值最后为0，说明经优化后系统满足稳定性、稳定裕度和阻尼比的要求。同理，当设置较小下垂系数初始值时，系统满足稳定性要求即C1为0，但C2不为0，因此阻尼比不满足要求。由于子目标相对权重系数L1明显大于L2，初次迭代后目标函数值明显小于初始下垂系数较大时的目标函数值。随着迭代次数的增加，目标函数值最后为0，说明系统是稳定的。同时，稳定裕度和阻尼比也满足要求。

当每台储能变流器设置较小的下垂系数（取值为0.35）时，优化前后系统发生第1 次和第2 次小扰动时，中、低频特征值分布如图2 所示。

图2 初始下垂系数较小时的特征值分布Fig.2 Eigenvalue distribution when initial droop coefficient is small

第1 次和第2 次小扰动特征值与阻尼比如附录D 表D3 所示。当施加第1 次小扰动时，系统最大实部特征值为-0.45+i31，施加第2 次小扰动时系统最大实部特征值为-3+i32。虽然满足局部稳定性要求，但系统第1 次扰动和第2 次扰动的最小阻尼比分别为0.01 和0.06，明显小于给定的阻尼比。因此，系统暂态过渡时间太长。

当每台储能变流器设置较大下垂系数（取值为1.37）时，优化前后系统发生第1 次和第2 次小扰动时，中、低频特征值分布如附录C 图C2 所示。系统阻尼比如附录D 表D4 所示，根据表D4 可知，下垂系数过小，对应的阻尼比满足要求。当发生第1 次小扰动时，系统特征值为-0.93+i135，可判断此时系统虽稳定，但稳定裕度不满足要求；当发生第2 次小扰动时，系统存在正的特征值为13+i135，可以判断此时发生扰动，系统不稳定。

下垂系数经协调优化后，每台储能变流器取值为0.88，系统特征值分布如附录C 图C2 所示，第1 次扰动和第2 次扰动后，特征值全部分布在左半平面，可判断系统发生小扰动后稳定，且经过2 次扰动后，系统实部的最大特征值分别为-9+i28 和-10+i32，满足稳定裕度x0要求。此外，通过计算可得，此时系统最小阻尼比为0.101，满足设定阻尼比要求。因此，验证了优化算法的有效性。

4.1.2 负荷扰动下垂系数仿真验证

当负荷发生扰动时，直流母线电压变化如附录C 图C3 所示。由图C3 可知，在1 s 时，直流微电网电阻性负荷减小为原来的40%，造成直流母线电压沿Idc-Udc下垂控制曲线升高；但在6 s 时，随着恒功率负荷增至原来的2 倍，优化前设置较大下垂系数，导致直流母线振荡发散，系统失稳。优化前设置较小的下垂系数，由于Idc-Udc下垂控制阻尼相对较弱，系统调节时间较长。而经优化后的下垂控制曲线在经过2 次小扰动后，直流母线电压经过振荡后趋向稳定。经负荷扰动后的各下垂控制单元功率变化如图C4 所示。仿真结果验证了理论分析的有效性。

4.2 光照扰动对直流微电网的影响

在1 s 时，施加第1 次小扰动，光照强度增大25%；在6 s 时，施加第2 次小扰动，本次扰动同时包含了2 种扰动，一是将光照强度增大33%，二是恒功率负荷减小到原来的1/3；在10 s 时，仿真结束。

4.2.1 光照扰动优化过程分析

当光照强度发生变化时，每台储能变流器设置较小下垂系数取值为0.78 时，优化前系统发生第1 次和第2 次小扰动时，中、低频特征值分布图如附录C 图C5 所示。

设置较小下垂系数未优化时，施加第1 次小扰动后，系统实部的最大特征值为-2 + i31，施加第2 次小扰动后，系统实部的最大特征值为-3+i32，虽然满足局部稳定性和稳定裕度要求，但通过计算得出系统第1 次扰动和第2 次扰动优化前后的阻尼比，如附录D 表D5 所示。优化前，系统的最小阻尼比分别为0.06 和0.09，明显小于给定的阻尼比。因此，可判断初始状态下系统暂态过渡时间太长。

当每台储能变流器设置较大下垂系数（取值为2.36）时，优化前系统发生第1 次和第2 次小扰动时，中、低频特征值分布如附录C 图C6 所示。系统阻尼比如附录D 表D6 所示，由表D6 可知，下垂系数过大，系统阻尼比满足要求。施加第1 次小扰动时，系统实部的最大特征值为8+i139，施加第2 次小扰动时，系统实部的最大特征值为10+i141，系统存在正的特征值，可以判断施加第1 次扰动和第2 次扰动时系统不稳定。

下垂系数经协调优化后，每台储能变流器取值为1.25 时，第1 次扰动和第2 次扰动后，特征值全部分布在左半平面，可判断系统发生小扰动后稳定，且经过2 次扰动后，系统实部的最大特征值分别为-5+i32 和-6+i33，满足稳定裕度x0要求。此外，通过计算可得，系统2 次小扰动的最小阻尼比分别为0.102 和0.125，满足设定阻尼比要求，验证了优化算法的有效性。

4.2.2 光照扰动下垂系数仿真验证

直流母线电压变化如图3 所示。图中：绿色、蓝色和红色分别代表优化前取较大下垂系数为2.36、优化前下垂系数为0.78 和优化后下垂系数为1.25的直流母线电压波形。

图3 下垂系数优化前后的直流母线电压波形Fig.3 Waveforms of DC bus voltage before and after droop coefficient optimization

由图3 可知，在1 s 时，直流微电网光伏增大25%，在进行小扰动分析时，将光伏模块等效成一种输出功率为负的特殊型恒功率负荷。因此，当光照强度增大时，系统总的恒功率负荷减小，造成直流母线电压沿Idc-Udc下垂控制曲线升高。但在6 s 时，随着光照强度增至原来的133%，且恒功率负荷减至原来的1/3，总体系统功率减小。优化前，设置较大的下垂系数，导致直流母线振荡发散，系统失稳；优化前，设置较小的下垂系数，由于Idc-Udc下垂控制阻尼相对较弱，系统调节时间较长。优化后的下垂控制曲线在经过2 次小扰动后，直流母线电压振荡后趋向稳定。各分布式单元功率变化如附录C 图C7 所示。仿真结果验证了理论分析的有效性。

5 实验验证

为了验证本文所提下垂系数优化方法的有效性，采用如图4 所示的实验平台，通过连接RTBOX在PLECS 中搭建了附录A 图A1 所示的直流微电网的仿真模型，实验系统参数与理论分析和仿真模型一致（如附录D 表D1 所示），设置与第4 章一致的小扰动，验证上述下垂系数协调优化结果的可行性。

图4 实验平台Fig.4 Experiment platform

5.1 负荷扰动对直流微电网的影响

系统发生2 次小扰动时，下垂系数优化前后直流母线电压波形测试结果如附录C 图C8 所示，其中，图C8（a）、图C8（b）和图C8（c）分别表示下垂系数优化前取值为1.37 和0.35、优化后取值为0.88 的直流母线电压波形。根据扰动后的波形稳定程度和调节时间可以看出，下垂系数经优化后，相较于初始时较大的下垂系数和经扰动后的系统稳定性明显提升；相较于初始时较小，下垂系数系统响应速度明显加快，验证了所提优化方法理论和仿真的正确性和有效性。

5.2 光伏扰动对直流微电网的影响

直流微电网光伏模块发生2 次小扰动时，下垂系数优化前后直流母线电压波形测试结果如附录C图C9 所示，其中，图C9（a）、图C9（b）和图C9（c）分别表示优化前下垂系数取值为2.36 和0.78、优化后取值为1.25 的直流母线电压波形。由图C9 可知，直流微电网在扰动前系统稳定运行，光伏模块发生扰动引起直流母线电压出现波动。通过下垂系数进行优化后，系统阻尼比和稳定性明显提升，验证了所提优化方法的正确性和有效性。