计及N-1 安全约束和系统恢复能力的发输电拓展规划
2022-12-13楼奕轩
楼奕轩,孙 磊,丁 明
(1. 合肥工业大学电气与自动化工程学院,安徽省合肥市 230009;2. 安徽省新能源利用与节能重点实验室(合肥工业大学),安徽省合肥市 230009)
0 引言
电力系统规划的主要任务是在预测未来电力增长状况、负荷曲线和电力分布情况的基础上,对未来电源和输电线路的投建做出合理的规划[1-2]。近年来,大停电事故仍时有发生且难以预测,随着大规模互联电网的发展,大停电事故可能波及的范围更大,停电事故所产生的后果更严重。因此,在发输电规划阶段中,如何提高电力系统恢复能力也是需要重点考虑的因素之一。
合理的发输电规划策略是电力系统安全经济运行的基础[3-6]。文献[7]提出一种基于灵活性资源概率分布的评估方法,并将该指标应用于输电网规划策略中。文献[8]提出一种应对协同攻击的电力系统发输电拓展随机规划,提高了规划效率和电力系统可靠性。文献[9]提出一种考虑电网灵活性和N-1 安全校验的5 层输电网规划优化模型,其中不确定性因素来自发电机组的出力。文献[10]提出一种计及N-1 安全校核的多阶段输电网扩展规划模型,提高了模型的求解效率。文献[11]提出了计及电网运行安全性、稳定性效率和供需平衡充裕性的电网结构及电源容量适应性指标,并建立了考虑网-源协同优化的输电网多目标规划模型。文献[12]针对输电线路、发电机以及柔性交流输电系统(flexible alternating current transmission system,FACTS)的规划问题,提出一种综合考虑灵活性、建设周期和成本等因素的两阶段鲁棒规划模型。综上所述,现有关于发输电规划的研究大多仅考虑了N-1 安全校核,并未考虑发生大停电事故后输电系统恢复能力能否满足要求这一因素。
近年来,国内外发生了多起大停电事故,给社会、经济带来极大的损失。例如,2021 年2 月,美国得州因受寒潮影响发生大规模的停电事故,导致当地的能源市场混乱,得州电价飙升了百余倍[13-14];2019 年8 月,英国发生大面积停电事故,导致英格兰与威尔士部分地区停电,部分城市地铁与城际火车停运、交通瘫痪,给日常生活造成了极大的不便[15-16];2016 年9 月,澳大利亚因极端恶劣天气导致一系列连锁电网故障,全州停电近50 h,造成了巨大的经济损失[17]。由于大停电事故危害巨大且难以预测,在进行电力系统规划时,应充分考虑电力系统恢复能力这一因素。
综上所述,本文提出一种计及N-1 安全约束和系统恢复能力的发输电拓展规划策略,所提出的策略能够同时兼顾N-1 安全校核以及大停电事故后电力系统的恢复能力。在发输电规划层面,建立了基于机会约束的发输电拓展规划模型;在系统运行层面,分别构建N-1 安全校核子问题模型和基于大停电事故的输电系统恢复能力校验子问题模型。本文所提出的模型为混合整数线性规划模型和线性规划模型,可利用商业求解器对所提出的模型进行高效求解。
1 发输电拓展规划的数学模型
发输电拓展规划模型的目标函数通常为最小化电力系统的投资与运行成本。考虑到负荷预测可能存在一定误差,需要考虑负荷波动这一不确定因素,本文引入机会约束处理负荷波动对发输电拓展规划策略的影响,进而构建基于机会约束的发输电拓展规划模型。
电力系统的安全运行不仅需要满足正常状态下的潮流约束,还需要满足N-1 预想故障状态下线路潮流不越限,因此,本文构建了N-1 安全校核子问题模型(子问题1)。此外,为了有效提高输电系统恢复能力,本文提出了基于大停电事故的输电系统恢复能力校验子问题模型(子问题2)。
发输电拓展规划模型和2 个子问题模型的关系如图1 所示。首先,求解基于机会约束的发输电拓展规划模型,得到初始的规划方案,将所得到的规划方案传递给2 个子问题模型,根据2 个子问题模型的解将可行割约束反馈给发输电拓展规划模型,并再次对发输电拓展规划模型进行求解,直到满足设定的终止条件。
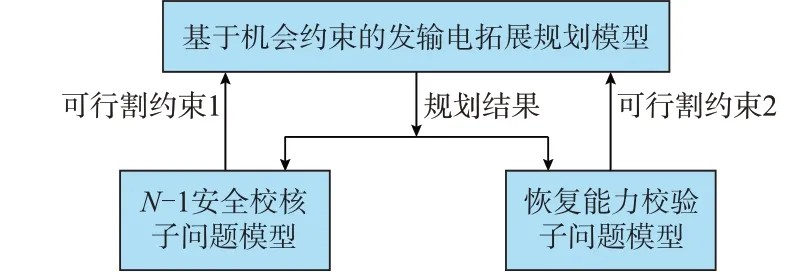
图1 发输电拓展规划模型与2 个子问题模型的关系Fig.1 Relationship between expansion planning model for power generation and transmission and two sub-problem models
1.1 基于机会约束的发输电拓展规划模型
发输电拓展规划模型的目标函数通常为最小化电力系统的投资与运行成本,如式(1)所示;投资费用和运行费用分别如式(2)和式(3)所示;贴现因子如式(4)所示。
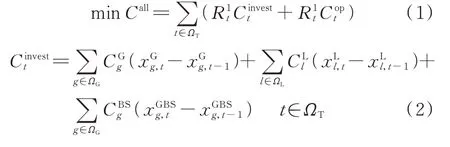

式中:ΩGi为位于节点i的发电机组集合;ΩB为节点集合;s(l)和r(l)分别为线路l的送端和受端;Pi,t为第t年节点i的负荷预测值。
式(7)表示第t年节点的功率平衡方程。
由于目标函数为最小化投资和运行费用,可将式(7)松弛,且当考虑负荷的不确定性时,可将式(7)描述为机会约束的形式,如式(8)所示。
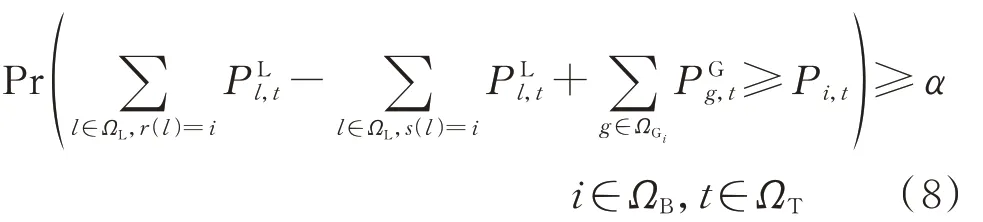
式中:Pr(·)为事件(·)发生的概率;α为给定的置信水平。
根据概率论相关理论,可将机会约束式(8)转换为 确 定 性 约 束 式(9),其 中,F-1(α,Pi,t)可 由 文 献[18]中所提出的方法计算得到。

式(10)和式(11)分别为基于big-M 方法的线路l传输功率的上下限约束和线路潮流的计算公式。
4)负荷约束:

式 中:γ为 负 荷 年 增 长 率;Pi,0为 当 前 年 节 点i的 负荷值。
式(12)为第t年负荷预测值的计算公式。
5)机组出力约束:

式中:NBS为黑启动机组的最小个数。
式(18)表示每年电力系统中至少有NBS台黑启动机组;式(19)表示第t年的黑启动机组必须是已投运的机组;式(20)表示黑启动机组g在第t年投运后,在后续阶段均为黑启动机组。
1.2 N-1 安全校核子问题模型

N-1 安全校核子问题模型的目标函数为最小化N-1 预想故障情况下系统的有功缺额,在数学上可以描述为:

式(23)和式(24)分别为在预想故障k中基于big-M 方法的线路l传输功率的上下限约束和线路潮流的计算公式。
3)节点相角约束:
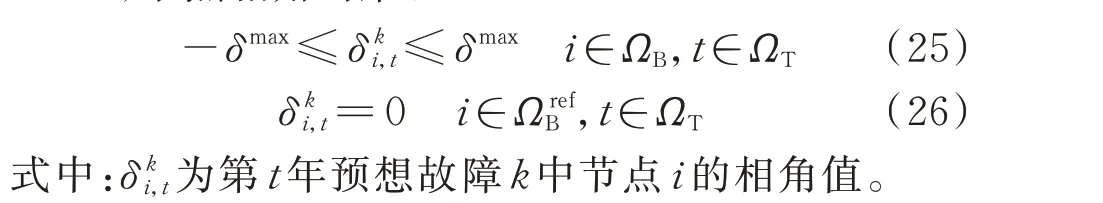
式(25)为在预想故障k中节点相角的上下限约束;式(26)表示在预想故障k中参考节点电压相角为0。
1.3 基于大停电事故的输电系统恢复能力校验子问题模型
输电系统的恢复能力可以通过所需的恢复时间进行评估。为了校验求解发输电拓展规划模型得到的规划方案在发生大停电事故后能否在限定时间内恢复,本节提出基于大停电事故的输电系统恢复能力校验子问题模型。其本质是在已知优化规划方案的前提下,以最小化停电损失为目标函数和以恢复时间不大于阈值为约束优化恢复方案。为了保证输电系统恢复能力校验子问题恒有解,引入辅助变量s3t,用于表征系统恢复时间阈值与实际恢复时间的差值。以下模型适用于t∈ΩT。

满足的约束条件包括以下12 类。1)电力系统恢复时间约束:

式(29)表示系统恢复所需时间与松弛变量之差不大于给定阈值。
2)电力系统恢复时间的计算:从发生大停电事故用户负荷全被切除到电力系统的负荷全部得以恢复,这一过程所耗费的时间为电力系统恢复时间,该时间可通过式(30)—式(32)计算得到。
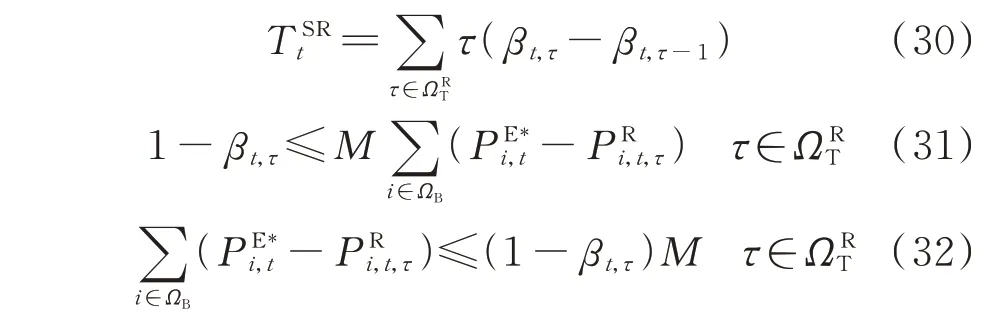
式中:βt,τ为引入的辅助布尔变量,其值为1 表示第t年τ时刻系统负荷已经完全恢复,其值为0 表示第t年τ时刻系统负荷还未完全恢复。
式(30)表示系统恢复时间的计算方法;式(31)和式(32)表示引入的辅助变量βt,τ与负荷总切除量的逻辑关系。
3)系统恢复阶段的节点平衡方程:


式(33)表示第t年系统恢复过程中满足的节点平衡方程。
4)系统恢复阶段的线路潮流约束:

式(34)和式(35)分别为系统恢复过程中基于big-M 方法的线路l传输功率的上下限约束和线路潮流的计算公式。
5)系统恢复阶段的节点相角约束:

式(36)为系统恢复过程中节点相角的上下限约束;式(37)表示系统恢复过程中参考节点电压相角为0。
6)负荷恢复量约束:

式(38)表示负荷恢复量的取值范围;式(39)表示在τ时刻的负荷恢复量应不小于τ-1 时刻的负荷恢复量。
7)发电机组的爬坡约束:

式(40)和式(41)分别表示机组g的上下爬坡约束。
8)电力网络连通性约束:
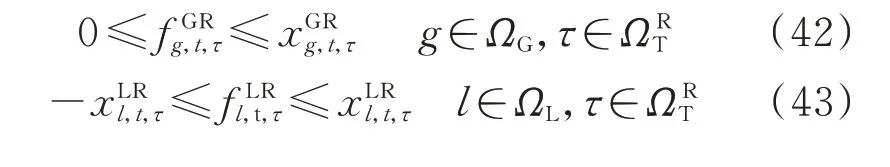

式(42)表示第t年τ时刻发电机组g的虚拟出力范围;式(43)表示第t年τ时刻输电线路l的虚拟传输功率的范围;式(44)表示第t年τ时刻节点虚拟潮流的平衡方程。
9)机组出力上下限约束:

式(46)为发电机组g启动时间的计算方法;式(47)表示发电机组g在恢复后经过等待并网时间后才能向系统输出功率。
11)变量间的逻辑关系约束:
式(48)表示如果在τ时刻发电机组g已恢复,则与发电机组g相连的节点i也已恢复;式(49)表示当与输电线路l相连的2 个节点中至少有一个节点在τ-1 时 刻 恢 复,输 电 线 路l才 能 在τ时 刻 恢 复;式(50)和式(51)表示如果输电线路l在τ时刻恢复,则与之相连的2 个节点i和j也在该时刻恢复;式(52)—式(54)分别表示在τ-1 时刻恢复的机组、线路和节点在τ时刻恢复状态不变;式(55)表示在系统恢复阶段与机组g相连的输电线路l的最短恢复时间不小于黑启动机组g的并网时间。
12)黑启动电源相关约束:

2 模型求解策略
2.1 模型线性化策略
由于式(3)含有非线性项,无法直接采用商业求解器高效求解,故对式(3)进行了线性化。引入2 个非负的辅助变量PL+l,t和PL-l,t,则有


因此,式(3)可描述为:
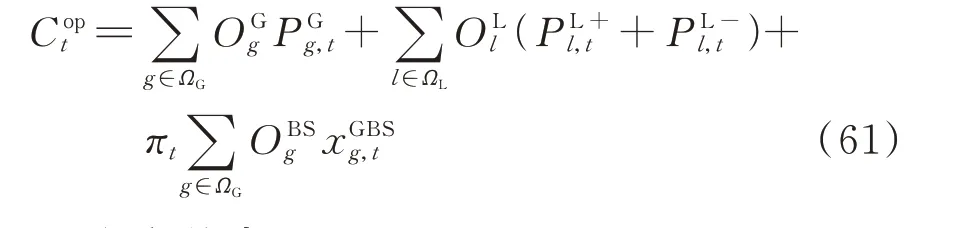
2.2 可行割约束
求解1.1 节提出的发输电拓展规划模型得到的规划方案可能无法满足N-1 安全校验以及大停电事故后最大恢复时间的要求。因此,可根据2 个子问题的解构建可行割,并传递给发输电拓展规划模型进行迭代求解。2 个子问题对应的可行割约束分别如式(62)和式(63)所示。
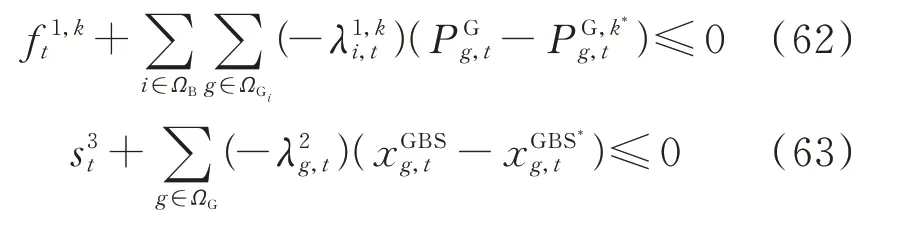
2.3 数学模型汇总
本文所提出的计及N-1 安全约束和系统恢复能力的发输电拓展规划策略由3 个模型构成,如表1所示。

表1 发输电拓展规划策略中的3 个模型Table 1 Three models in expansion planning strategy for power generation and transmission
2.4 求解算法流程
本文所构建的发输电拓展规划模型和输电系统恢复能力校验子问题模型均为混合整数线性规划模型,所提出的N-1 安全校核子问题模型为线性规划模型,故选用GUROBI 商业求解器求解。本文所提出的发输电拓展规划策略的求解流程图如图2所示。
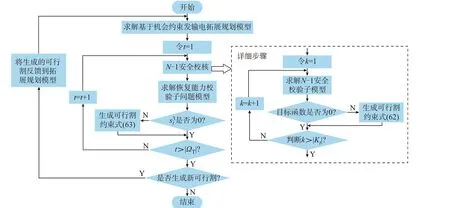
图2 发输电拓展规划策略的求解流程图Fig.2 Flow chart of solving expansion planning strategy for power generation and transmission
具体的求解步骤如下:
步骤1:求解基于机会约束的发输电扩展规划模型,令t=1。
步骤2:令k=1。
步骤3:求解N-1 安全校验子问题模型,若目标函数为0,则跳转至步骤4,否则生成可行割约束式(62)。
步骤4:判断是否遍历完成所有N-1 预想故障,是则转至步骤5,否则令k=k+1,转至步骤3。
步骤5:求解大停电事故后的输电系统恢复能力校验子问题模型,若满足s3t=0,则转至步骤6,否则生成可行割约束式(63)。
步骤6:判断t是否大于规划年限,若是则跳转至步骤7,否则令t=t+1,转入步骤2。
步骤7:判断是否有新的可行割生成,如果是则将可行割反馈到基于机会约束的发输电扩展规划模型,并跳转至步骤1,否则求解过程结束。
3 算例分析
以Garver 6 节点系统和IEEE 57 节点系统为例,来说明所提方法的有效性。算法运行环境如下:处理器为英特尔酷睿Intel Core(TM)i7-10870H、内存为16 GB 的笔记本电脑。在AMPL 建模平台上构建模型,并调用GUROBI 9.1.2 求解模型。
3.1 Garver 6 节点系统
Garver 6 节点系统的数据详见文献[19]。该系统的初始拓扑以及候选线路和机组如图3 所示。

图3 Garver 6 节点系统拓扑Fig.3 Topology of Garver 6-bus system
系统含有6 个节点、8 条已投运的输电线路和4 台已投运的机组,已投运机组和候选机组均分布在节点1、3 和6。已投运的发电机组总装机容量为630 MW,候选机组的总装机容量为630 MW,当前年负荷总量为760 MW。假设负荷年增长率为3%,规划年限为10 年,负荷预测值服从正态分布,置信水平设为0.95。恢复时间间隔设为10 min。候选发电机组和候选输电线路分别为8 台和26 条,具体参数分别如表2 和表3 所示。

表2 候选机组参数Table 2 Parameters of candidate units
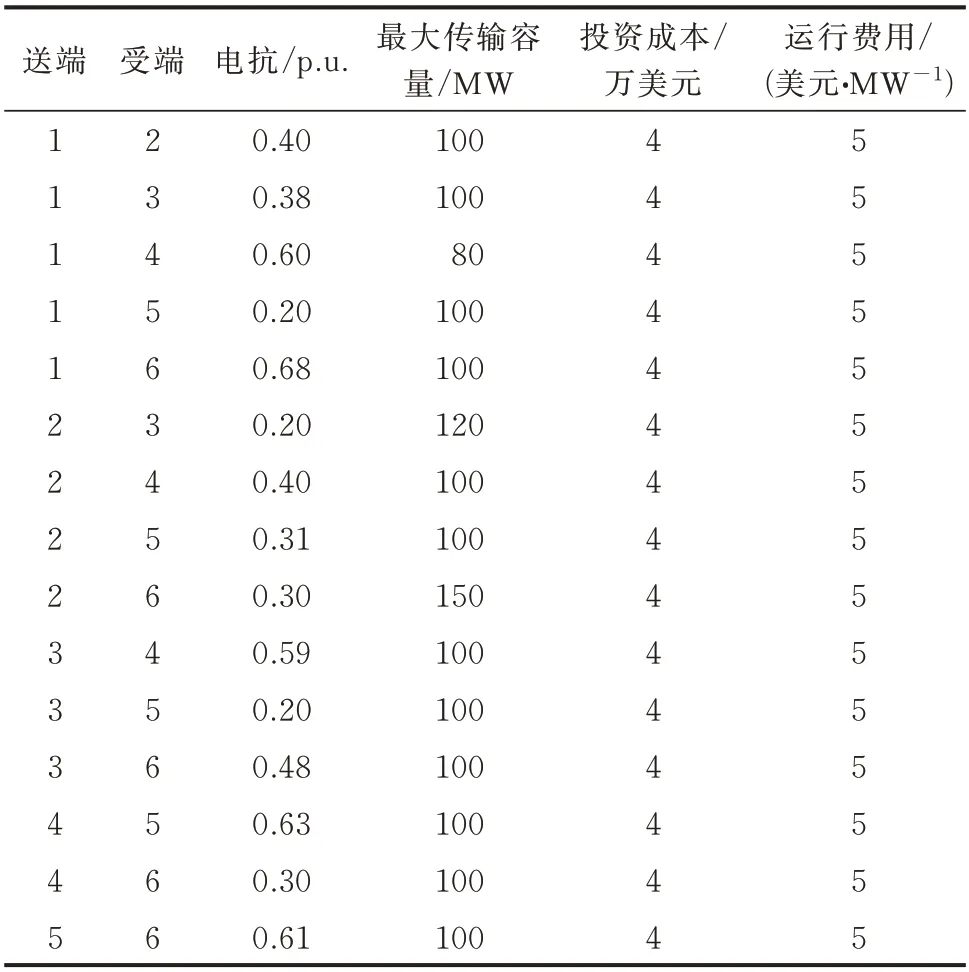
表3 候选线路参数Table 3 Parameters of candidate lines
求解计及N-1 安全约束和系统恢复能力的发输电拓展规划模型,获得最优的规划方案,求解时间为180.08 s,总的投资与运行费用为5 491.78 万美元。表4 展示了Garver 6 节点系统的规划结果,包括不同规划年新投建的机组和线路。由表4 可以看出,在规划年限内共需新投建5 台发电机组和4 条输电线路。随着负荷逐年增长,需新投入一定数量的机组和线路从而满足负荷增长的需求。表5 展示了第1 年的规划方案中切除l2-1的一回路前后的部分输电线路功率的变化情况。从表5 可以看出,切除线路l2-1的一回路后,系统中与该线路相连的线路潮流会发生变化,其中线路l2-3的潮流增加了近1 倍。
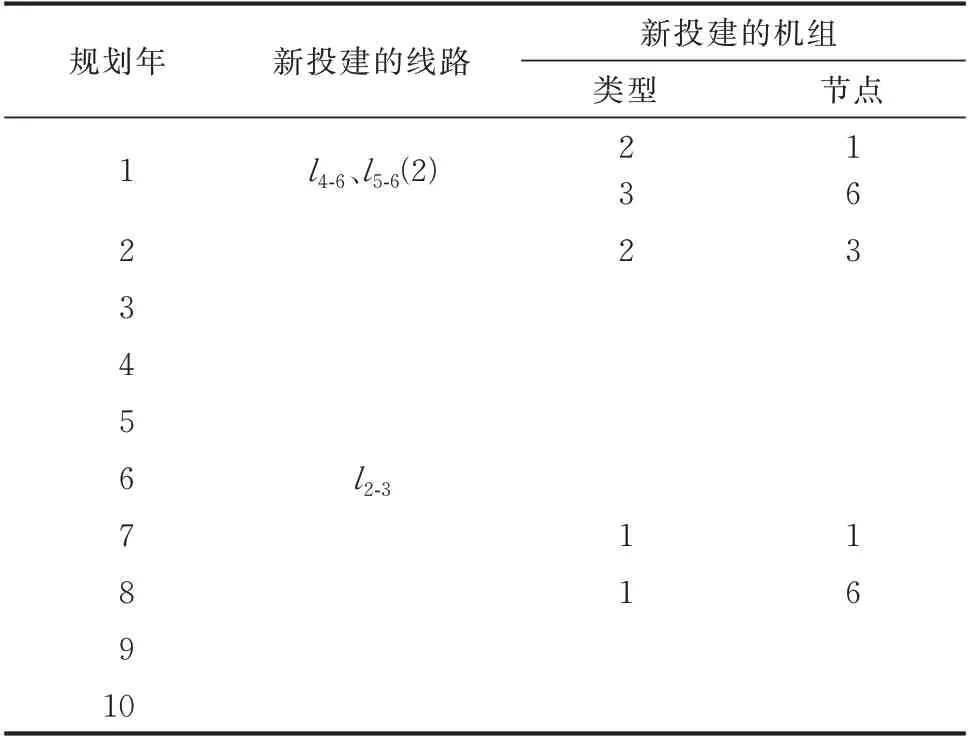
表4 Garver 6 节点系统的规划结果Table 4 Planning results of Garver 6-bus system

表5 第1 年的规划方案中切除l2-1的一回路前后部分输电线路功率潮流的变化Table 5 Power flow changes through selected lines before and after cutting off one line connecting buses 2 and 1 in planning scheme for the first planning year
图4 展示了2 个子问题模型的辅助变量随迭代次数的变化情况。在图4 中,左侧y轴为子问题1 模型中辅助变量之和,右侧y轴为子问题2 模型中的辅助变量值。由图4 可以看出,随着迭代次数的增加,2 个子问题模型的辅助变量值总体呈现下降趋势,经过7 次迭代计算最终收敛为0。在第3 次迭代计算结果中,基于大停电事故的输电系统恢复能力校验子问题模型的辅助变量值为0,在发生大停电事故时所需的恢复时间也满足要求,但N-1 安全校核子问题的辅助变量值不为0,所以需要继续迭代。第7 次迭代计算得到的2 个子问题的松弛变量均为0,故经过7 次迭代计算后所得的规划结果满足N-1 安全校核,且在发生大停电事故后所需的恢复时间也满足要求。
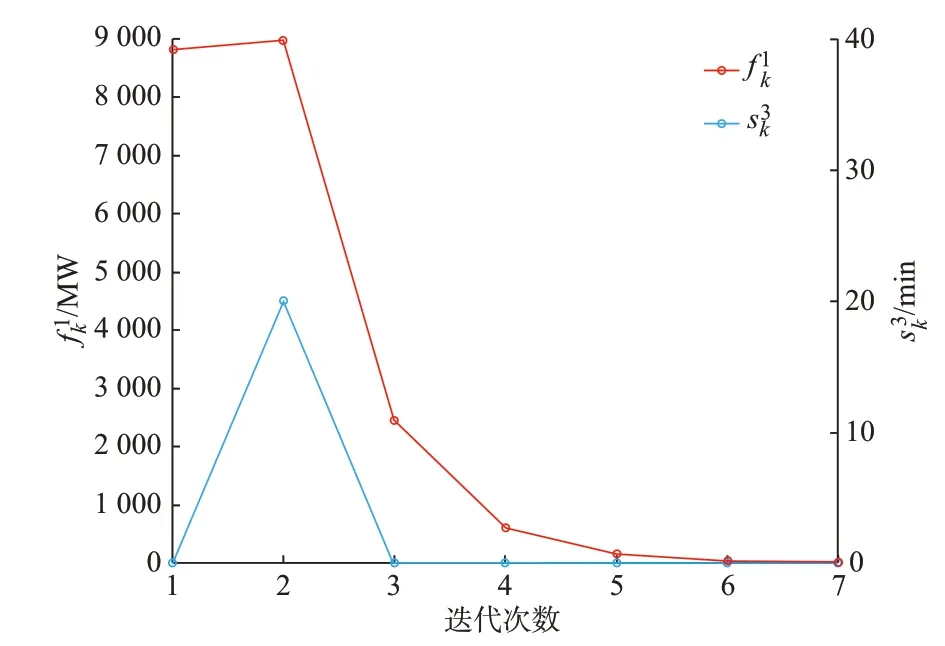
图4 2 个子问题模型的辅助变量随迭代次数的变化Fig.4 Changes of auxiliary variables of two subproblem models with different iteration times
图5 展示了输电系统在第1 个规划年发生大停电事故的恢复过程。通过求解所提出的模型,可得发电机组G8为最优的黑启动机组,在黑启动机组G8启动后逐步恢复系统中其他机组、线路及负荷。由图5 可以看出,经过120 min 后系统中的非黑启动机组和线路全部得以恢复。
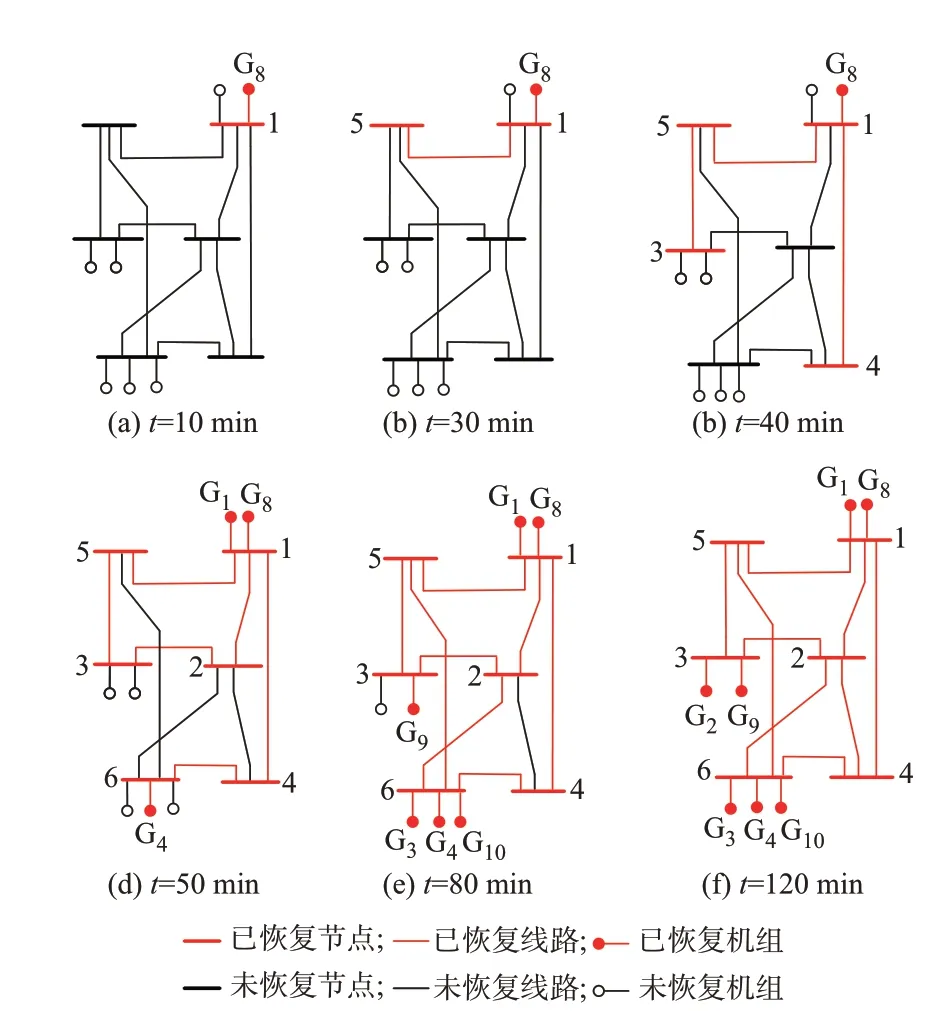
图5 发生大停电事故后输电系统的恢复过程Fig.5 Restoration process of power transmission system after blackout occurs
表6 展示了采用不同规划策略得到的系统恢复时间对比。由表6 可以看出,采用考虑系统恢复能力的规划策略得到的输电系统在发生大停电事故后的恢复时间在各个规划年均小于采用不考虑系统恢复能力的规划策略的结果,其中在第10 年恢复时间差值最大,最大差值为40 min。
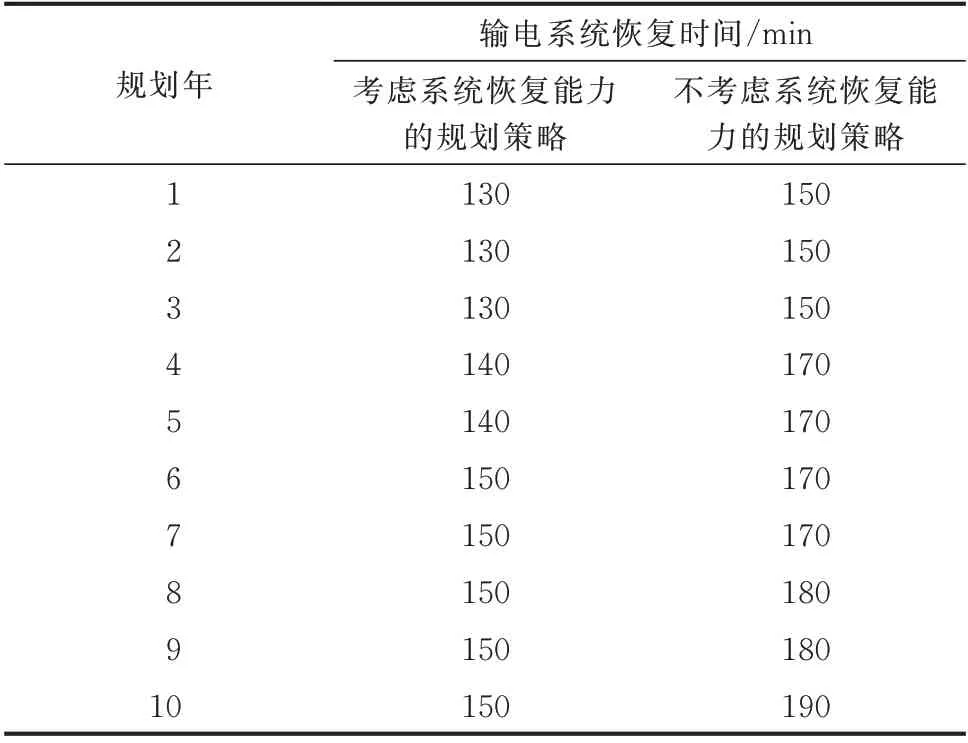
表6 采用不同规划策略得到的系统恢复时间对比Table 6 Comparison of system restoration time with different planning strategies
3.2 IEEE 57 节点系统
本节采用IEEE 57 节点系统对所提出的发输电拓展规划模型的有效性进行验证。该系统共包含57 个节点、80 条已投运的输电线路和7 台已投运的机组。设候选机组7 台、候选线路15 条。设初始负荷为额定负荷的1.5 倍,负荷增长率为3%。
求解计及N-1 安全约束和系统恢复能力的发输电拓展规划模型,可得最优的发输电拓展规划方案,如表7 所示。求解所提出的模型可得,发输电规划方案的最小投资和运行费用为6 055.94 万美元,模型求解时间为2 011.64 s,在电力系统中规划了2 个黑启动机组,在规划年中系统恢复时间最长为2.3 h。由表7 可以看出,在规划年限内共新投建4 台发电机组和3 条输电线路。

表7 IEEE 57 节点系统的规划结果Table 7 Planning results of IEEE 57-bus system
4 结语
本文提出了计及N-1 安全约束和系统恢复能力的发输电拓展规划策略,并将该策略分解为基于机会约束的发输电拓展规划模型、N-1 安全校核子问题模型和基于大停电事故的输电系统恢复能力校验子问题模型。通过迭代计算可得最优的发输电规划方案。算例结果表明,根据本文的规划方法得到的发输电规划方案能够满足N-1 安全校核和大停电事故后的系统恢复能力校核,兼顾经济性和安全性。
本文所构建的发输电拓展规划方案考虑了N-1 安全校核和系统恢复能力,但未考虑在系统恢复阶段的N-1 安全校核,后续将进一步研究考虑系统恢复阶段N-1 安全校核的电力系统恢复能力评估及在发输电拓展规划策略中的应用。
