基于Fe-Ga合金敏感栅式应力传感器*

曾宇露，刘方晨，王 欢，万家鑫，黄森林

(1.南昌工程学院 电气工程学院,江西 南昌 330099；2.江西省精密驱动与控制重点实验室，江西 南昌 330099)

0 引 言

随着科技的发展，传感器在工业、航空、医疗等领域有着越来越重要的作用，而应力传感器的应用最为广泛。常见的应力传感器有电阻应变式[1,2]、振弦式[3,4]和压电式传感器[5,6]。电阻应变式传感器虽然具有结构简单、灵敏度高的特点，但在测量大型结构应力时对电桥结构及布线要求高；振弦式应力传感器虽然结构简单、安装简便，但其体积较大，不适合精密构件的应力测量；压电式传感器具有输出信号大、频率响应高的特点，但其不能用于静态测量，信号处理电路复杂。各领域控制及检测系统的可靠性取决于传感器的性能，因此,研发一种灵敏度高、体积小、使用寿命长的应力传感器有着重要意义。

磁致伸缩应力传感器是以磁致伸缩材料作为敏感元件，利用维拉里(Villari)效应对应力进行测量，具有灵敏度高、过载性能好、使用便捷等特点，能够满足各领域对传感器性能的要求[7～9]。而铁镓(Fe-Ga)合金具有较好的物理性能，磁导率随应力变化显著，以Fe-Ga设计的传感器具有更好的性能[10,11]。

因此，本文以敏感栅结构的Fe-Ga合金磁致伸缩片作为敏感元件设计了敏感栅式应力传感器，并通过有限元仿真及实验分析了所设计的传感器性能。

1 结构设计

设计的磁致伸缩应力传感器由Fe-Ga合金片、霍尔传感器、线圈及U型磁芯构成。其中，Fe-Ga片作为敏感元件，需具有足够高的柔度，厚度为0.15 mm，并采用敏感栅结构对Fe-Ga片进行设计，其结构如图1所示。

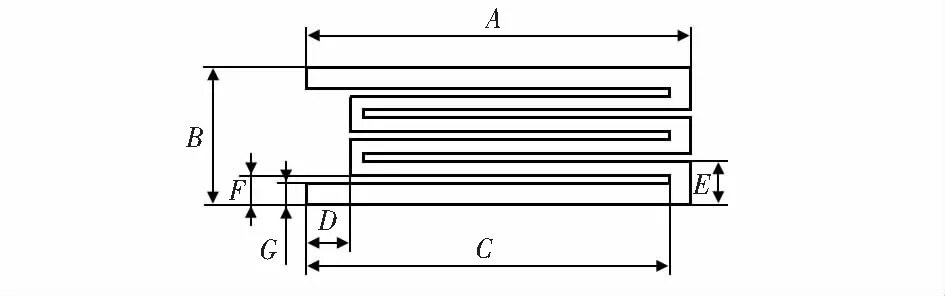
图1 Fe-Ga片敏感栅结构

为减小传感器体积，采用单边U型磁芯设计；使用高灵敏度霍尔元件作为转换元件，可对磁通量进行静、动态测量；利用多匝线圈产生稳定可调的偏置磁场。其整体结构设计如图2所示。

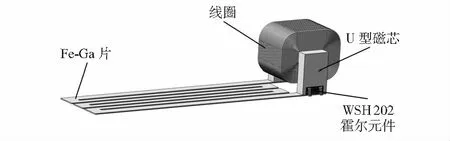
图2 Fe-Ga应力传感器整体结构

结合图1、图2，Fe-Ga应力传感器主要结构参数如表1所示。

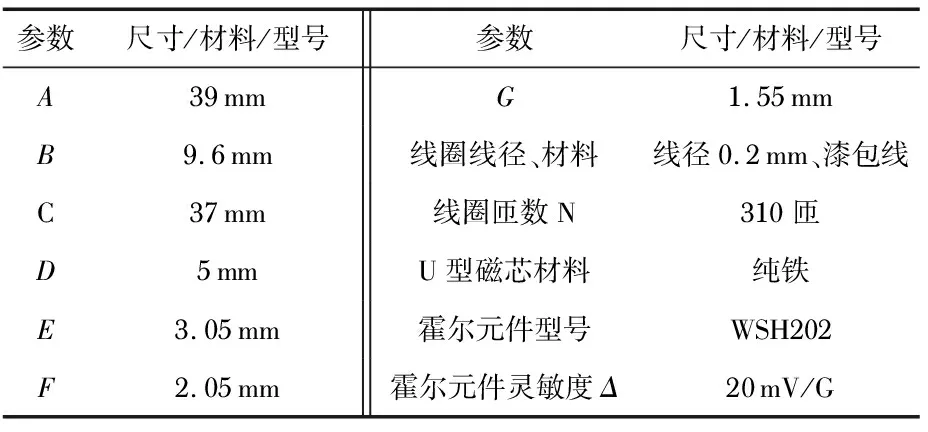
表1 Fe-Ga应力传感器结构参数

2 建 模

磁致伸缩应力传感器对应力的检测基于磁致伸缩材料的Villari效应，磁致伸缩材料在恒温环境下的线性压磁方程表示为[12]

(1)

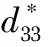
(2)

由式(1)、式(2)可得磁通量与应力σ间的关系

B=σ(d33-μσ/(EGd33))+μσε/d33

(3)

式中 磁致伸缩片的应变ε=ΔL/L，ΔL和L分别为磁致伸缩材料在偏置磁场作用下的长度变化和初始长度，ΔL可表示为[14]

(4)

式中μ0为真空磁导率，B0为偏置磁场下的初始磁通密度，与偏置线圈电流大小及磁路磁阻有关。根据霍普金森定律，磁路的磁通量

φ=BSh=NI/rt

(5)

式中B为通过霍尔元件表面的磁通密度，N为线圈匝数，I为线圈激励电流，Sh为霍尔元件截面积，rt为磁路总磁阻。磁路总磁阻由磁芯磁阻rF和Fe-Ga片磁阻rG组成[15]

(6)

式中 下标i和j分别为磁芯、Fe-Ga片各截面标号，li和lj为垂直各截面方向的磁芯和Fe-Ga片长度，Si和Sj为磁芯、Fe-Ga片各截面对应的面积大小，μF为磁芯材料的磁导率，μG为Fe-Ga片各截面垂直方向上对应的起始磁导率。假设Fe-Ga片各截面面积相等，为SG；且铁芯各截面面积相等，为SF。则由式(3)、式(4)可得初始磁通密度

(7)

当传感器粘结于被测物表面时，假设被测物为长方体，且受平行于传感器长度方向的外力F作用。假设外力由被测物传递至传感器的过程中无损耗且传感器受力均匀，则Fe-Ga片所受应力σ=F/S，S为Fe-Ga片表面积。根据式(3)、式(4)、式(7)，可得传感器输出电压U为

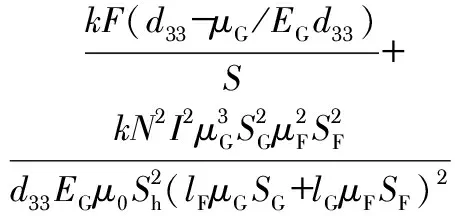
(8)

式中k为霍尔元件灵敏度。对式(8)求导，可得应力F变化与传感器输出电压U变化的关系

(9)

3 有限元仿真分析

3.1 仿真设置

建立图3所示的仿真模型。

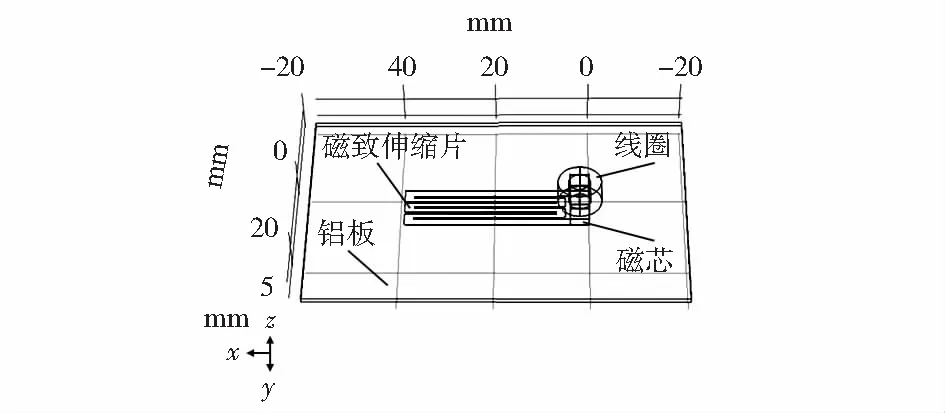
图3 仿真模型

模型中，试验铝板板长80 mm，宽50 mm，厚1 mm。图3模型包裹在直径为60 mm的球形空气域中。仿真过程中，固定铝板左端，在右端以125 N的间隔在x轴方向上施加-625～625 N的力，线圈设置为310匝，线圈线径设置为0.2 mm，线圈通入电流分别设置成0.10,0.15,0.20 A，进行多次仿真计算。模型各部分材料属性设置如表2所示。

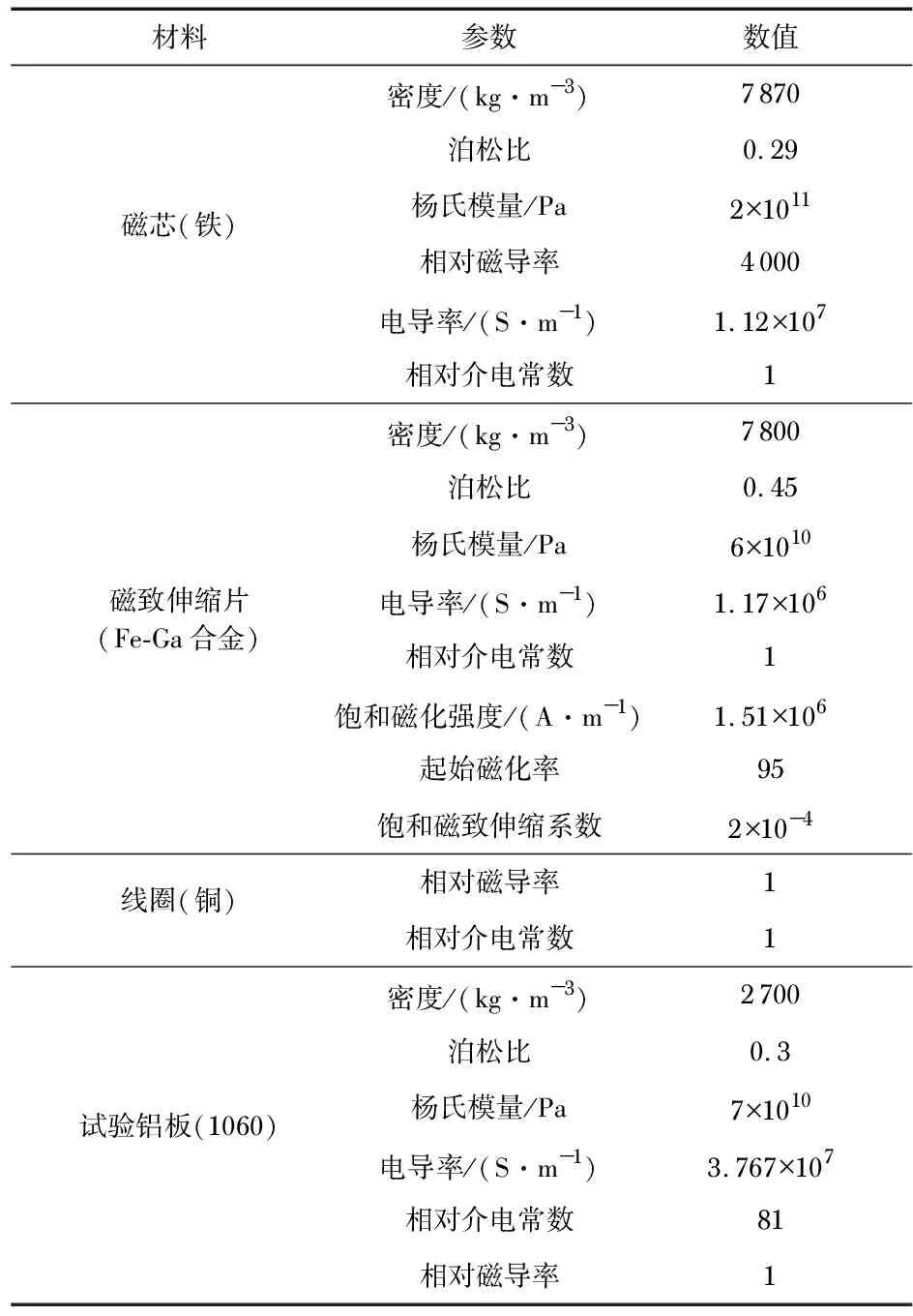
表2 材料属性设置

3.2 力—磁耦合仿真结果与分析

为求解磁致伸缩应力传感器输出特性，对传感器进行力磁耦合分析。给线圈通入0.2 A电流时，在0 N和625 N拉力作用下，磁致伸缩传感器磁路中磁通密度分布分别如图4所示。

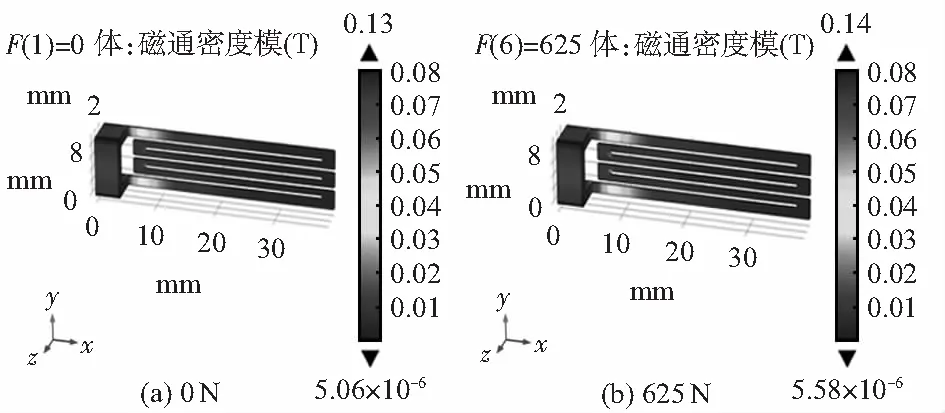
图4 不同拉力下磁通密度分布

由图4可知，磁通密度在磁芯与磁致伸缩片连接处有集中，且随着磁场路径增大而减小。当施加在铝板上的拉力由0 N增加至625 N时，最大磁通密度由0.13 T增至0.14 T，即磁致伸缩片磁导率增大。

为比较不同电流，不同应力作用下，霍尔传感器输出电压大小，对磁芯单边与磁致伸缩片接触面设置探针,取磁通密度平均值B，并在有限元软件中定义输出电压U=kB。不同电流、不同应力作用下有限元仿真结果如图5所示。

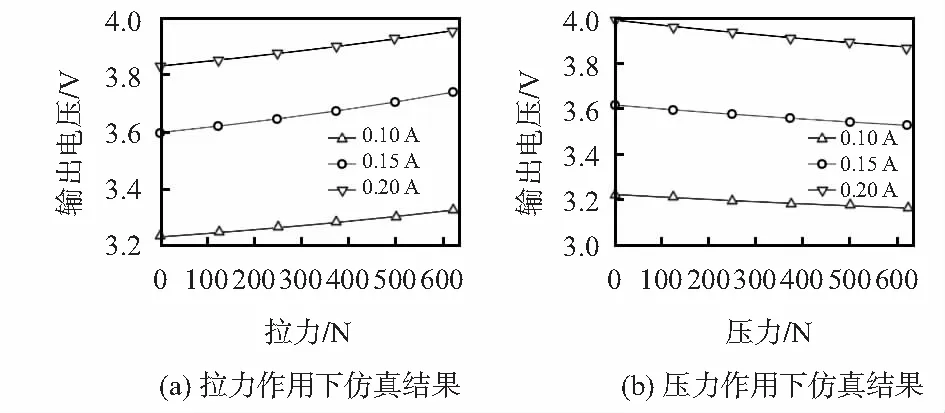
图5 磁致伸缩传感器输出电压仿真结果

由仿真结果可知，传感器输出电压随拉力的增大线性增大，随压力的增大线性减小。结合力学仿真结果，设计的磁致伸缩应力传感器在0.10，0.15，0.20 A线圈电流下，拉力灵敏度分别为9.87，14.8，13 mV/MPa，压力灵敏度分别为6.25，9.32，12.43 mV/MPa。有限元仿真采用非线性模型计算，且考虑了传感器磁场的非均匀分布及磁致伸缩现象带来的影响，因此，有限元仿真的传感器灵敏度是变化的，且电压呈现非线性变化。

4 实验结果与分析

根据设计的磁致伸缩应力传感器尺寸结构，制作的样机如图6所示。

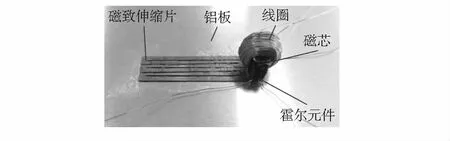
图6 磁致伸缩应力传感器样机

样机中，磁致伸缩片与铝板之间由810结构胶连接。试验平台搭建如图7所示。其中，稳压直流电源给线圈分别提供0.10，0.15，0.20 A的可调节电流，电源变压器给霍尔元件提供5 V直流电压。

图7 试验平台

万能试验机夹持铝板两端，在不同线圈电流下，以125 N为间隔，施加0～625 N的拉力和压力。示波器采集的霍尔传感器输出电压与拉力(压力)的关系如图8所示。

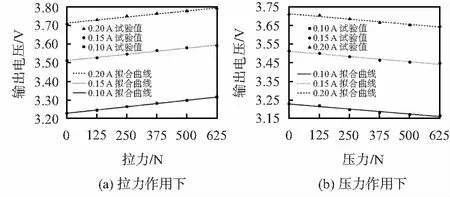
图8 对应不同激励电流的霍尔传感器输出电压

由实验结果可知，传感器输出电压随拉力的增大线性增大，随压力的增大线性减小。结合力学仿真结果，设计的磁致伸缩应力传感器在0.10，0.15，0.20 A线圈电流下，拉力灵敏度分别为9.12，8.7，8.52 mV/MPa，压力灵敏度分别为7.08，7.34，7.49 mV/MPa，具有高灵敏度。

传感器输出电压基本呈线性变化，在非均匀磁场下的传感器，其灵敏度随线圈电流变化，与有限元仿真结果较为吻合。输出电压的变化与有限元仿真结果较为吻合，但仍存在误差。其误差由以下因素导致：1)传感器加工精度误差；2)万能试验机试验过程中会产生低频振动，影响输出信号稳定性；3)万能试验机夹头具有导磁性，影响传感器磁路；4)磁致伸缩片与铝板之间由结构胶连接，影响力的传导。

5 结 论

设计了一种敏感栅式磁致伸缩应力传感器，其整体结构简单，由Fe-Ga片、霍尔元件、线圈、磁芯构成，能够贴于测试件表面测量测试件表面应力。实验表明：在0.10，0.15，0.20 A线圈电流激励下，传感器拉力灵敏度分别为9.12，8.7，8.52 mV/MPa，压力灵敏度分别为7.08，7.34，7.49 mV/MPa，具有较高灵敏度。传感器具有体积小、灵敏度高的特点，且除试验用的粘结方式外，传感器还可通过焊接固定在结构件上，实现长期实时在线测量，具有较高的应用研究价值。