机油品质的可计算电容测量方法研究*
2022-12-10李俊杰赵思泽黄文超王铭伟
李俊杰, 刘 泽,赵思泽, 黄文超, 王铭伟
(北京交通大学 电子信息工程学院,北京 100044)
0 引 言
机油品质的优劣程度直接影响发动机的稳定性和安全性[1]。油品检测常用方法有介电常数法[2]、气相色谱法[3]、近红外光谱法[4]、颗粒法[5]等,这些方法需要进行采样并送到实验室后,使用对应仪器进行分析,存在依赖检测仪器、步骤繁琐、效率低、不够轻量化等不足[6,7],无法满足航空、航天等实时性和准确性要求高的应用场合[8]。
其中,介电常数法较其他方法虽然有结构简单,分辨力强的优点,但该方法中电容传感器存在动态特性差,误差源多的缺点,而可计算电容在国际上作为标定基本单位的阻抗基准,其不确定度达到了10-8量级[9],由于可计算电容的容值只与其轴向的有效长度有关,因此,在结构上只引入了单一误差源[10],具有较高的精度和稳定度,根据此特点,电容传感器可以小型化,从而使介电常数法轻量化。
2001年,韩国Lee R D等人采用可计算电容测量已知液体的介电常数(介电常数范围为2~4),并根据测量结果拟合了介电常数表达式,证明了可计算电容可以用于液体介电常数的测量[11],但缺少相应定量的描述,除此之外,于航、王颖等人将可计算电容用于燃料液位测量[12,13],Rehman M等人设计出高灵敏度的线性微压力计[14]。
本文旨在从可计算电容理论出发,建立可计算电容传感器的数学模型,推导对应介电常数表达式,建立有限元仿真模型进行验证,开展机油配比实验进一步分析所设计传感器的特性。
1 可计算电容介电常数传感器设计
1.1 基本原理与结构
机油的工作温度在70~110 ℃之间,为了在机械接触面之间可以形成油膜减小磨损,机油具有一定的粘稠度,针对机油的工作环境特点,选用耐热高温、表面光滑不易粘连、绝缘性能好的石英晶体管作为可计算电容的支撑材料,可计算电容介电常数传感器横截面如图1所示。

图1 可计算电容介电常数传感器截面示意
本文设计的可计算电容介电常数传感器基于可计算电容理论[15],该理论指出对于截面为任意形状的无限长柱面导体,用4个无限小的绝缘间隙δ1,δ2,δ3,δ4将柱面分为四部分,此时相对面1,3与2,4分别构成的电容C1,C2,且满足式(1)
exp(-πC1/ε0)+exp(-πC2/ε0)=1
(1)
式中ε0=8.854 187 817×10-12F/m为真空介电常数。
当C1≈C2时,定义C1,C2的平均值Cx为计算电容的输出值,即

(2)
式中C0=(ε0εrln 2)/π,ΔC=C1-C2,εr为电容内介质的相对介电常数。当计算电容处于真空环境时C0=1.953 549 043pF/m,从式(2)可知,当C1,C2数值相近时,可计算电容的输出值Cx与C0的差值为二阶及以上小量,意味着可计算电容的容值与其横截面的大小无关,当有效长度确定且足够精确时,可计算电容的输出有较高的稳定性。
图1中,D1,D2分别为石英晶体管内径、外径,D3为传感器整体的直径;在传感器外部包裹屏蔽层减小外界的电磁干扰。4个极板在石英晶体管表面轴向等间距放置,构成可计算电容的基本结构,相对的电极由一个高电位电极和一个低电位电极组成;等位环放置在传感器上下两端,用于减小电容的边缘效应,提高可计算电容介电常数传感器的线性度和灵敏度[16];此外,根据可计算电容与其横截面大小无关的特性,可将该传感器结构小型化,方便安装到发动机的油路系统中进行检测。
1.2 数学模型建立
由于石英晶体管有一定的厚度,所以在建模过程中必须考虑石英晶体管对传感器输出的影响,假设将图1所示的可计算电容放在真空环境下,且极板上为单位电势,建立极坐标系下拉普拉斯方程式(3)
(3)
其解为可计算电容传感器内的电位分布,如式(4)
dmr-m)×(amcosmθ+bmsinmθ)
(4)
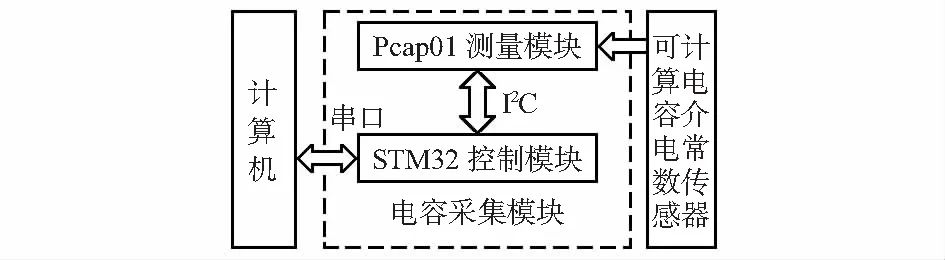
根据图1,可计算电容介电常数传感器在径向上可以被分成3个区域:区域1:2r (5) (6) (7) 根据区域1和区域2的边界D1处电势相等,区域2和区域3边界D2处电势相等,式(7)可整理为 (8) 则电荷量密度为 (9) 当r=R3时,对式(8)积分可得到单位长度极板上的电荷量Q,如式(10)所示 (10) C= (11) 进一步化简得式(12) (12) (13) 式中KR为可计算电容传感器规格尺寸有关的修正系数,当可计算电容传感器规格确定后,KR为一确定常数;将相对介电常数为εr的物质作为长度为l的计算电容的介质时,上式可简化为式(14) (14) 因为电极的厚度极薄,所以把R2=R3代入式(13),则修正系数 (15) 整理式(14)得 (16) 由式(16)可知,可计算电容介电常数传感器的容值C与其中的介质的介电常数εr为二次函数的关系。 使用在工程领域广泛应用的有限元分析法对所设计的传感器进行建模仿真分析,建立与图1对应的模型。极板1上施加电压为1 V的激励,其余3个极板设置为0 V,在此激励条件下求解得到传感器的网格分布如图2(a)所示,电势等值云图如图2(b)所示、电场矢量分布如图3所示。 图2 传感器的网格分布和电势等值云图 图3 电位矢量图 由图2(a)可知,靠近激励极板的网格划分密集,远离激励极板的网格划分稀疏,说明越靠近激励极板电场强度越强;图2(b)中,激励极板电势最大为1 V,其余极板电势为0 V,且电势为波纹状由最大值到最小值向其余极板扩散。图3中,电场强度的方向由激励极板指向0电位极板,并且在邻极板的边缘处电场强度达到最大,为3.1 V/mm,此现象是因为在相邻极板的边缘处发生了边缘效应,极板边缘处的电荷分布不均匀导致[17,18]。 发动机运行状况复杂多样,发动机中的机油状况也不尽相同,但是随着机油中氧化物,金属碎屑等污染物的增多,机油的极性变大,介电常数也会随之增加,假设机油的介电常数范围为1.01~1.03,并设置为有限元仿真模型中介质的介电常数,表1为仿真结果和通过式(16)解算得到的计算电容传感器输出值。 [16]Brian Z. Tamanaha,On the Rule of Law: History, Politics,Cambridge: Cambridge University Press, 2004,p.113. 由表1可以看出,随着介质相对介电常数的增加,传感器的电容输出越大;在介电常数为单一变量的前提下,实验值和仿真值存在约0.024 pF的误差,误差主要来源为有限元分析法将模型进行离散化分析,引入了离散化误差[19],但曲线趋势基本相同,对比理论和仿真的结果,可以初步验证,可计算电容介电常数传感器模型建立的正确性。 基于可计算电容的机油品质检测系统包括3部分,可计算电容介电常数传感器,电容采集模块以及计算机。其中,电容采集模块由PCap01测量模块和STM32控制模块组成,系统的结构如图4所示。 图4 机油品质检测系统组成框图 PCap01是由德国ACAM公司推出的电容数字转换(capacitive to digital conversion,CDC)芯片,有21位数据有效位,在参考电容为10 pF,测量速率为5 Hz时,电容测量的精度为6 aF[20]。 选择比较典型的轿车发动机机油作为实验样本,将行驶1万公里后完全废弃的机油按10 %~100 %的体积分数与同一品牌的全新机油混合并充分混合均匀,模拟机油在使用过程中的劣化过程,配比油样作为可计算电容介电常数传感器中的介质。 在室温为21℃环境中,利用机油品质检测系统对可计算电容介电常数传感器进行去程和回程的6次重复性实验,实验结果箱线图如图5所示。由图5可知,随着废弃机油体积分数的增加,可计算电容的容值增加趋势明显,与理论计算和有限元仿真分析的结论一致,实验数据中,6次实验数据取平均后得到满量程范围为yFS=2.6×10-4pF。 图5 去程、回程重复性实验箱线图 正反行程中的最大重复性误差ΔRmax=1×10-5pF,则可计算电容介电常数传感器的重复性误差为γR=±3.85 %。取每组实验的均值进行去程回程对电容值的对比,最大差值为ΔHmax=1×10-5pF,可计算电容介电常数传感器的迟滞误差为γL=±1.92 %。根据式(16)可计算出实验中油样的介电常数范围为1.012 76~1.015 48,由于变化范围较小,可以将该段近似为直线,用最小二乘法进行线性拟合,结果为 C=0.095 86εr+0.014 34 (17) 实验曲线和拟合曲线的最大非线性误差为ΔLmax=1.6×10-10pF,则可计算电容介电常数传感器的线性度为γL=±4.4×10-4%。可计算电容介电常数传感器以及电容测量平台的A类测量不确定度为7×10-7。 本文针对机油品质测量传统介电常数法中电容传感器误差源多的问题,通过理论分析,推导了可计算电容介电常数传感器模型,使用有限元仿真分析初步验证了传感器模型的合理性;在机油配比实验中,对所设计的可计算电容介电常数传感器进行误差特性分析,由实验结果得传感器的重复性误差、迟滞误差、不确定度,均在合理范围内,并且介质的介电常数在一定范围内,具有较好的线性度。2 有限元仿真验证
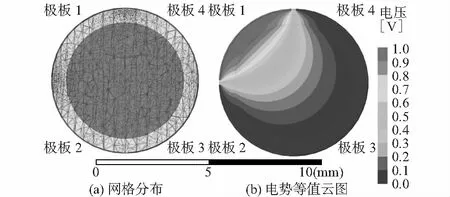

3 机油品质检测系统设计
4 机油配比实验

5 结 论
